算法第十二天-最大整除子集
最大整除子集
题目要求

解题思路
来自[宫水三叶]
根据题意:对于符合要求的[整除子集]中的任意两个值,必然满足[较大数]是[较小数]的倍数
数据范围是 1 0 3 10^3 103,我们不可能采取获取所有子集,再检查子集是否合法的暴力搜解法。
通常递归做不了,我们就往[递推]方向取考虑。
由于存在[整除子集]中任意两个值必然存在倍数/约数关系的性质,我们自然会想到对nums进行排序,然后从集合nums中从大到小进行取数每次取数只考虑到当前决策的数是否与[整除子集]中的最后一个数成倍数关系即可。
这时候你可能会想枚举个数作为[整除子集]的起点,然后从前往后遍历一遍,每次都将符合[与当前子集最后一个元素成倍数]关系的数加入答案。
但是这样子的做法只能确保获得[合法解],无法确保得到的是[最长整除子集]
得到这个反例:[9,18,54,90,108,180,360,540,720],如果按照我们上述逻辑,我们得到的是 [9,18,54,108,540] 答案(长度为 5),但事实上存在更长的「整除子集」: [9,18,90,180,360,720](长度为 6)。
其本质是因为同一个数的不同倍数之间不存在必然的[倍数/约数关系],而是存在[具有公约数]的性质,这会导致我们[模拟解法]错过最优解
因此当我们决策到某个数nums[i]时(nums已排好序),我们无法直接将nums[i]直接接在符合[约数关系]的,最靠近位置i的数后面,而是要检查位置i前面的所有符合[约数关系]的位置,找到一个已经形成[整除子集]长度最大的数。换句话说,当我们对nums排好序号并从前往后处理时,已经形成的[整数子集]长度是多少,然后从中选一个最长的[整除子集],将nums[i]接在后面(前提是符合[倍数关系])
动态规划
基于上述分析,我们不难发现这其实是一个序列DP问题:某个状态的转移依赖于与前一个状态的关系。即nums[i]能否接在nums[j]后面,取决于是否满足nums[i] % nums[j] == 0条件
可以看作是[最长上升子序列]问题的变形题。
定义f[i]为考虑前i个数字,且以第i个数为结尾的最长[整数子集]长度。
我们不失一般性的考虑任意位置i,存在两种情况:
- 如果在
i之前找不到符合条件nums[i]%nums[j]==0的位置j,那么nums[i]不能接在位置i之前的任何数的后面,只能自己独立作为[整除子集]的第一个数,此时状态转移方程为f[i]=1; - 如果在
i之前能够找到符合条件的位置j,则取所有符合条件的f[i]的最大值,代表如果希望找到以nums[i]作为结尾的最长[整除子集],需要将nums[i]接到符合条件的最长的nums[j]后面,此时状态转移方程为f[i]=f[j]+1
同时由于我们需要输出具体方案,需要额外使用g[]数组来记录每个状态是由哪个状态转移而来的。
定义g[i]为记录f[i]是由哪个下标的状态转移而来的,如果f[i] = f[j] + 1,则有g[i] = j
对于求方案数的题目,多开一个数组来记录状态从何转移而来是常见的手段。当我们求得所有的状态值止呕,可以对f[]数组进行遍历,取得最长[整除子集]长度和对应下标,然后使用g[]数组进行回溯,取得答案。
代码
class Solution:def largestDivisibleSubset(self, nums: List[int]) -> List[int]:nums.sort()n = len(nums)f,g = [0] *n,[0]*nfor i in range (n):#至少包含自身一个数,因此起始长度为1,由自身转移而来length,prev =1,ifor j in range(i):if nums[i] %nums[j] ==0:# 如果能接在更长的序列后面,则更新[最大长度]&[从何转移而来]if f[j] +1>length:length +=1prev =j# 记录【最终长度】& 【从何转移而来】f[i] =lengthg[i] =prev#遍历所有的f[i],取得[最大长度]和【对应下标】max_len = idx = -1for i in range(n):if f[i] >max_len:idx =imax_len =f[i]#使用g[]数组回溯出具体方案ans=[]while len(ans)<max_len:ans.append(nums[idx])idx = g[idx]ans.reverse()return ans复杂度分析
时间复杂度: O ( n 2 ) O(n^2) O(n2)
空间复杂度: O ( n ) O(n) O(n)
相关文章:

算法第十二天-最大整除子集
最大整除子集 题目要求 解题思路 来自[宫水三叶] 根据题意:对于符合要求的[整除子集]中的任意两个值,必然满足[较大数]是[较小数]的倍数 数据范围是 1 0 3 10^3 103,我们不可能采取获取所有子集,再检查子集是否合法的暴力搜解法…...

简单易懂的PyTorch 损失函数:优化机器学习模型的关键
目录 torch.nn子模块Loss Functions详解 nn.L1Loss 用途 用法 使用技巧 注意事项 代码示例 nn.MSELoss 用途 用法 使用技巧 注意事项 代码示例 nn.CrossEntropyLoss 用途 用法 使用技巧 注意事项 代码示例 使用类别索引 使用类别概率 nn.CTCLoss 用途 …...

Kubernetes/k8s的存储卷/数据卷
k8s的存储卷/数据卷 容器内的目录和宿主机的目录挂载 容器在系统上的生命周期是短暂的,delete,k8s用控制创建的pod,delete相当于重启,容器的状态也会回复到初始状态 一旦回到初始状态,所有的后天编辑的文件都会消失…...
【漏洞复现】锐捷RG-UAC统一上网行为管理系统信息泄露漏洞
Nx01 产品简介 锐捷网络成立于2000年1月,原名实达网络,2003年更名,自成立以来,一直扎根行业,深入场景进行解决方案设计和创新,并利用云计算、SDN、移动互联、大数据、物联网、AI等新技术为各行业用户提供场…...
)
Android - 串口通讯(SerialPort)
最早的博客Android 模拟串口通信过程_launch virtual serial port driver pro-CSDN博客里就是用过 Google 提供的 demo,最近想再写个其他的demo发现用起来有点麻烦,还需要导入其他 module,因此在网上找到了Android-SerialPort-API: https://g…...

如何使用設置靜態住宅IP
靜態住宅IP就是一種靜態的、分配給住宅用戶的IP地址。與動態IP地址不同,靜態住宅IP一旦分配給用戶,就會一直保持不變,除非ISP(Internet Service Provider,互聯網服務提供商)進行手動更改。那麼,…...
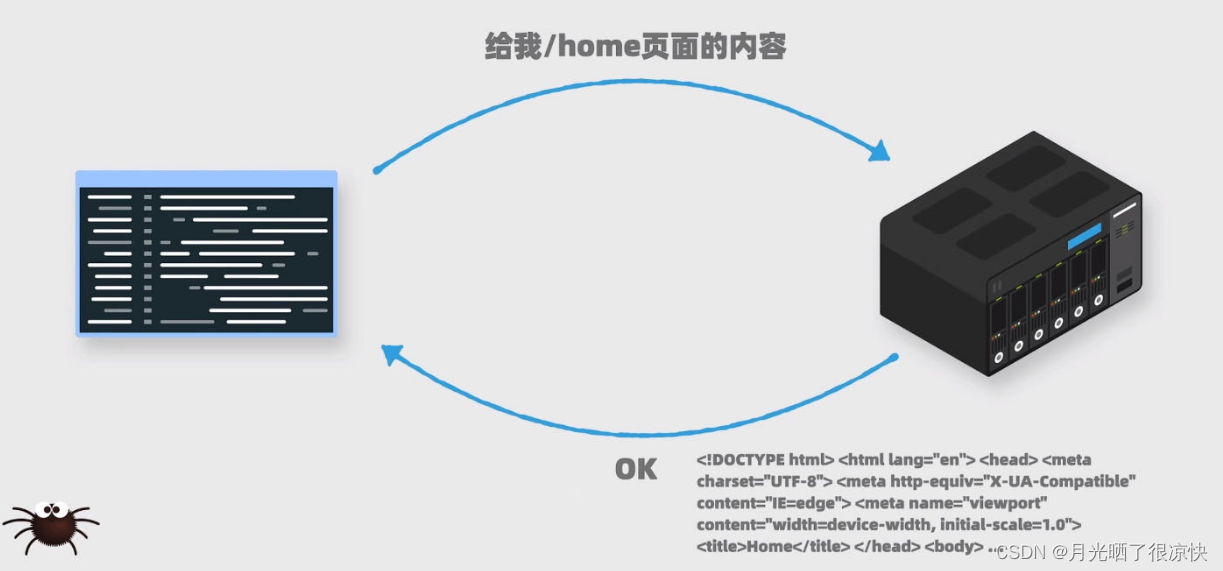
在学习爬虫前的准备
1. 写一个爬虫程序需要分几步 获取网页内容。 我们会通过代码给一个网站服务器发送请求,它会返回给我们网页上的内容。 在我们平时使用浏览器访问服务器内容是,本质上也是向服务器发送一个请求,然后服务器返回网页上的内容。只不过浏览器还会…...
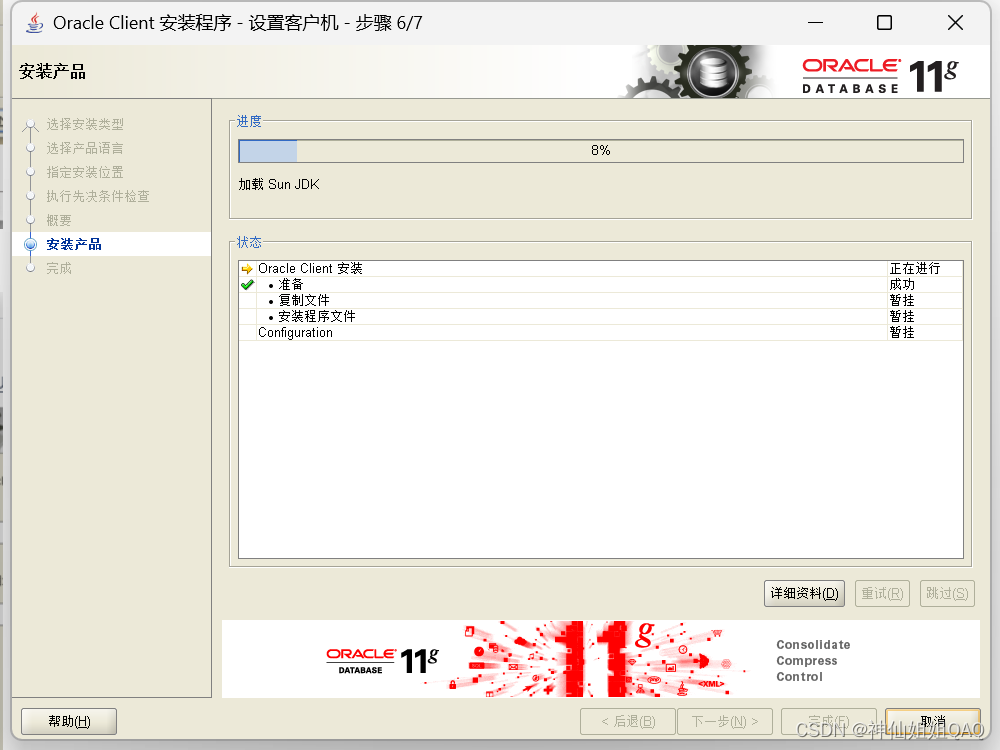
windows下安装oracle-win-64-11g超详细图文步骤
官方下载地址:点这里 1.根据自己电脑情况,解压64或者32位客户端,以及database压缩包 2.解压后双击执行database文件夹下的setup.exe 3.详细的安装步骤 (1)数据库安装 一、配置安全更新 电子邮件可写可不写…...

Go模板后端渲染时vue单页面冲突处理
go后端模版语法是通过 {{}} ,vue也是通过双花括号来渲染的,如果使用go渲染vue的html页面的时候就会报错,因为分别不出来哪个是vue的,哪个是go的,既可以修改go的模板语法 template.New("output").Delims(&qu…...

笔记本摄像头模拟监控推送RTSP流
使用笔记本摄像头模拟监控推送RTSP流 一、基础安装软件准备 本文使用软件下载链接:下载地址 FFmpeg软件: Download ffmpeg 选择Windows builds by BtbN 一个完整的跨平台解决方案,用于录制、转换和流式传输音频和视频。 EasyDarwin软件:Download Easy…...

鸿蒙开发已解决-ArkTS编译时遇到arkts-no-obj-literals-as-types错误
文章目录 项目场景:问题描述原因分析:解决方案:解决方案1解决方案2此Bug解决方案总结项目场景: 在开发鸿蒙项目过程中,遇到了arkts-no-obj-literals-as-types,总结了自己和网上人的解决方案,故写下这篇文章。 遇到问题: rkTS编译时遇到arkts-no-obj-literals-as-type…...
实现目标检测中的数据格式自由(labelme json、voc、coco、yolo格式的相互转换)
在进行目标检测任务中,存在labelme json、voc、coco、yolo等格式。labelme json是由anylabeling、labelme等软件生成的标注格式、voc是通用目标检测框(mmdetection、paddledetection)所支持的格式,coco是通用目标检测框࿰…...

一文读懂JVS逻辑引擎如何调用规则引擎:含详细步骤与场景示例
在当今的数字化时代,业务逻辑和规则的复杂性不断增加,这使得逻辑引擎和规则引擎在处理业务需求时显得尤为重要。逻辑引擎和规则引擎通过定义、解析和管理业务逻辑和规则,能够帮助企业提高工作效率、降低运营成本,并增强决策的科学…...

苹果应用上架是否需要软件著作权?
苹果应用上架是否需要软件著作权? 摘要 随着移动互联网的发展,苹果应用在市场上占据了很大份额。但是,很多开发者在上传苹果应用到App Store时,都会遇到一个问题,即是否需要进行软著申请?本文将深入探讨这…...
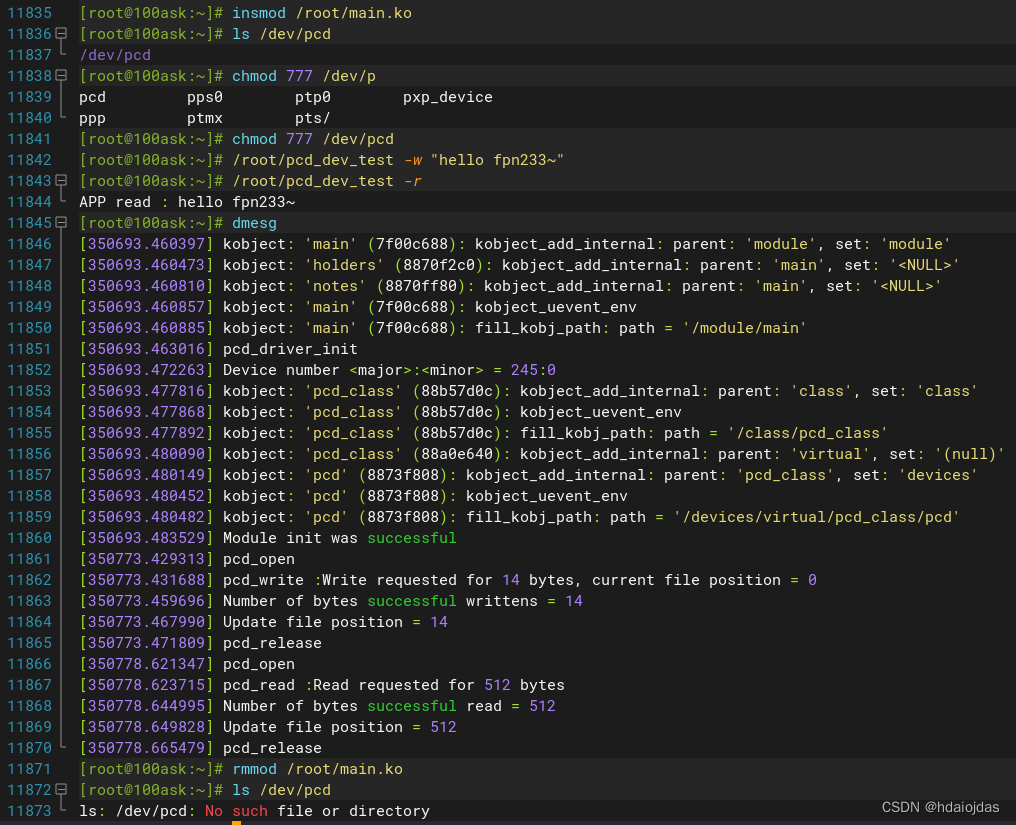
LDD学习笔记 -- Linux字符设备驱动
LDD学习笔记 -- Linux字符设备驱动 虚拟文件系统 VFS设备号相关Kernel APIs动态申请设备号动态创建设备文件内核空间和用户空间的数据交换系统调用方法readwritelseek 写一个伪字符设备驱动在主机上测试pcd(HOST)在目标板上测试pcd(TARGET) 字符驱动程序用于与Linux内核中的设备…...

杰理AC63串口收发实例
在event.h文件中预定义串口消息 #define DEVICE_EVENT_FROM_MY_UART ((M << 24) | (Y << 16) | (U << 8) | \0)在app_spp_and_le.c文件里对SYS_DEVICE_EVENT做处理,添加收到DEVICE_EVENT_FROM_MY_UART消息时的处理函数my_rx_handler(); cas…...
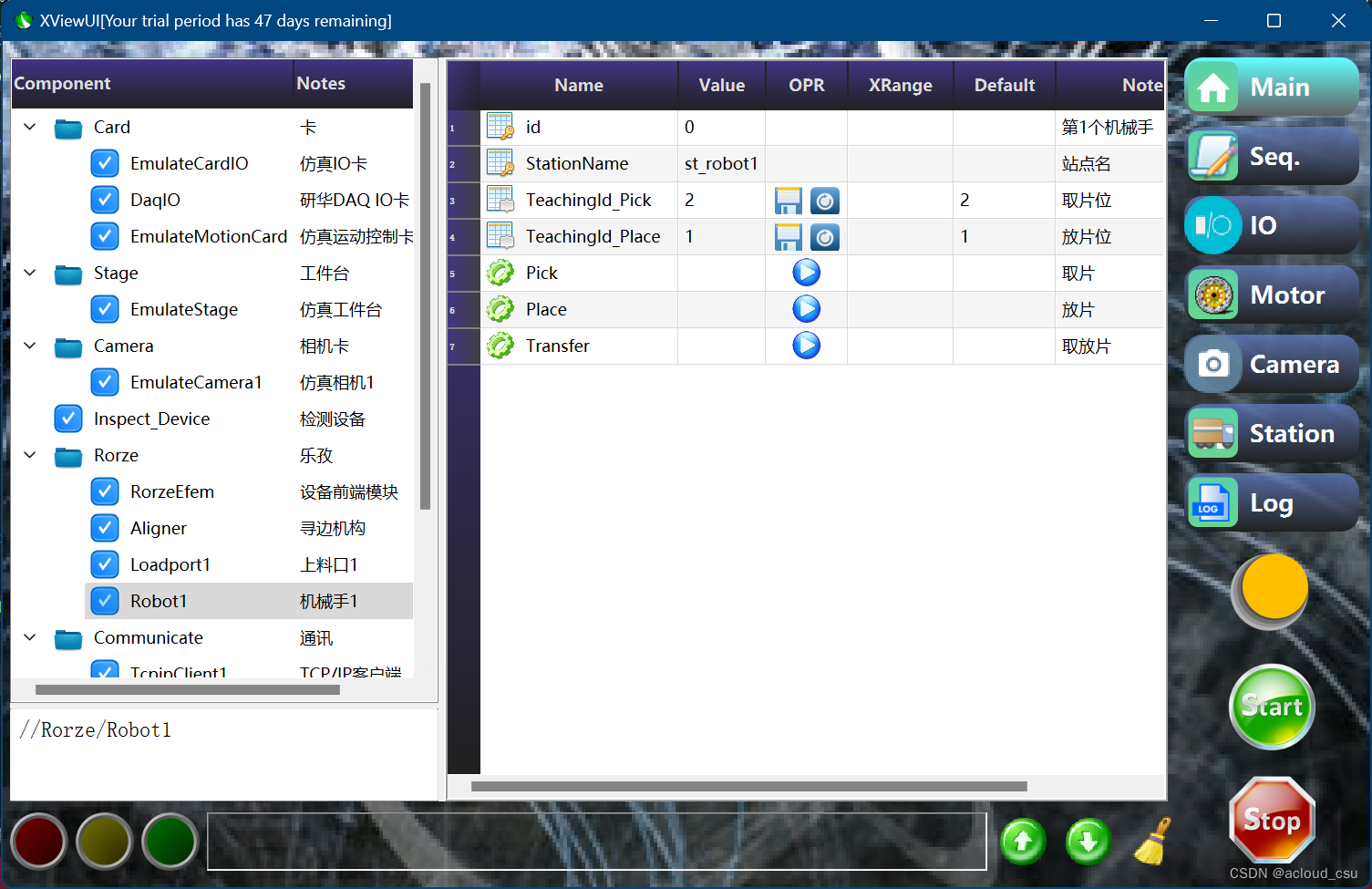
麦芯(MachCore)开发教程1 --- 设备软件中间件
黄国强 2024/1/10 acloud163.com 对任何公司来说,在短时间内开发一款高质量设备专用软件,是一件不太容易做到的事情。麦芯是笔者发明的一款设备软件中间件产品。麦芯致力于给设备厂商提供一个开发工具和平台,让客户快速高效的开发自己的设备专…...

reset命令
作用:将当前 HEAD 重置为指定状态 Git 的四个区域 Workspace:工作区,就是你平时存放项目代码的地方;Index / Stage:暂存区,用于临时存放你的改动,事实上它只是一个文件,保存即将提交到文件列表…...
LinuxIO基础知识与概念)
Linux内核--进程管理(十二)LinuxIO基础知识与概念
目录 一、引言 二、IO基本概念 ------>2.1、内存空间划分 ------>2.2、读写操作 ------>2.3、用户态切换到内核态的3种方式 三、PIO&DMA ------>3.1、PIO 工作原理 ------>3.2、DMA 工作原理 四、缓冲IO和直接IO ------>4.1、缓冲 IO ------&…...
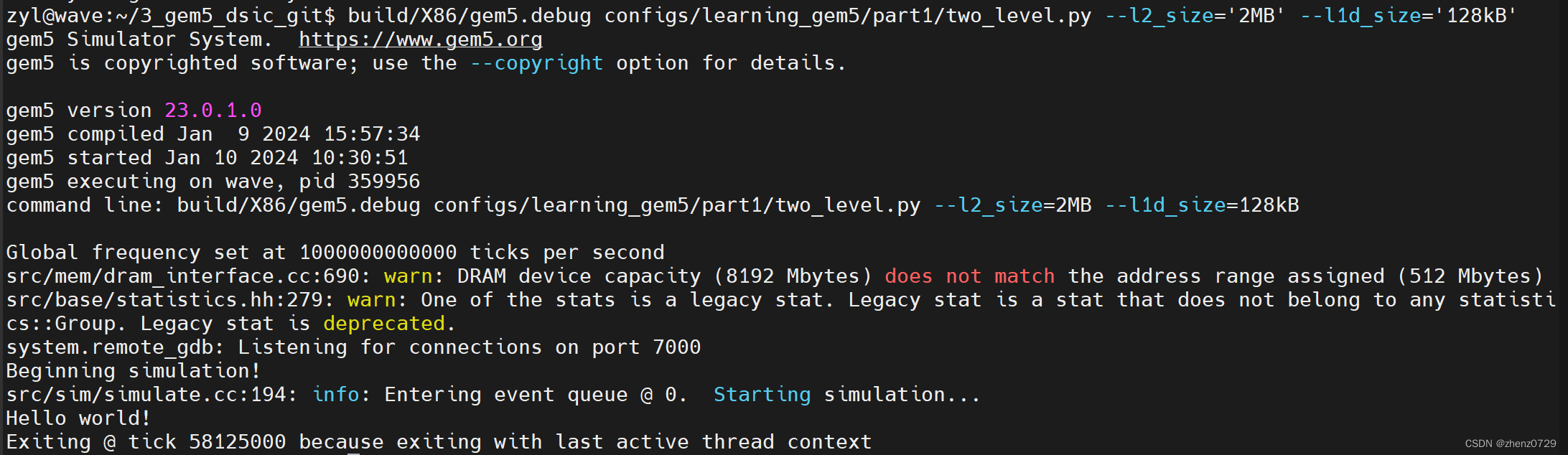
gem5学习(11):将缓存添加到配置脚本中——Adding cache to the configuration script
目录 一、Creating cache objects 1、Classic caches and Ruby 二、Cache 1、导入SimObject(s) 2、创建L1Cache 3、创建L1Cache子类 4、创建L2Cache 5、L1Cache添加连接函数 6、为L1ICache和L1DCache添加连接函数 7、为L2Cache添加内存侧和CPU侧的连接函数 完整代码…...

微信小程序之bind和catch
这两个呢,都是绑定事件用的,具体使用有些小区别。 官方文档: 事件冒泡处理不同 bind:绑定的事件会向上冒泡,即触发当前组件的事件后,还会继续触发父组件的相同事件。例如,有一个子视图绑定了b…...

C++:std::is_convertible
C++标志库中提供is_convertible,可以测试一种类型是否可以转换为另一只类型: template <class From, class To> struct is_convertible; 使用举例: #include <iostream> #include <string>using namespace std;struct A { }; struct B : A { };int main…...

LeetCode - 394. 字符串解码
题目 394. 字符串解码 - 力扣(LeetCode) 思路 使用两个栈:一个存储重复次数,一个存储字符串 遍历输入字符串: 数字处理:遇到数字时,累积计算重复次数左括号处理:保存当前状态&a…...

对WWDC 2025 Keynote 内容的预测
借助我们以往对苹果公司发展路径的深入研究经验,以及大语言模型的分析能力,我们系统梳理了多年来苹果 WWDC 主题演讲的规律。在 WWDC 2025 即将揭幕之际,我们让 ChatGPT 对今年的 Keynote 内容进行了一个初步预测,聊作存档。等到明…...

使用 Streamlit 构建支持主流大模型与 Ollama 的轻量级统一平台
🎯 使用 Streamlit 构建支持主流大模型与 Ollama 的轻量级统一平台 📌 项目背景 随着大语言模型(LLM)的广泛应用,开发者常面临多个挑战: 各大模型(OpenAI、Claude、Gemini、Ollama)接口风格不统一;缺乏一个统一平台进行模型调用与测试;本地模型 Ollama 的集成与前…...

MacOS下Homebrew国内镜像加速指南(2025最新国内镜像加速)
macos brew国内镜像加速方法 brew install 加速formula.jws.json下载慢加速 🍺 最新版brew安装慢到怀疑人生?别怕,教你轻松起飞! 最近Homebrew更新至最新版,每次执行 brew 命令时都会自动从官方地址 https://formulae.…...

Bean 作用域有哪些?如何答出技术深度?
导语: Spring 面试绕不开 Bean 的作用域问题,这是面试官考察候选人对 Spring 框架理解深度的常见方式。本文将围绕“Spring 中的 Bean 作用域”展开,结合典型面试题及实战场景,帮你厘清重点,打破模板式回答,…...

Python竞赛环境搭建全攻略
Python环境搭建竞赛技术文章大纲 竞赛背景与意义 竞赛的目的与价值Python在竞赛中的应用场景环境搭建对竞赛效率的影响 竞赛环境需求分析 常见竞赛类型(算法、数据分析、机器学习等)不同竞赛对Python版本及库的要求硬件与操作系统的兼容性问题 Pyth…...

篇章二 论坛系统——系统设计
目录 2.系统设计 2.1 技术选型 2.2 设计数据库结构 2.2.1 数据库实体 1. 数据库设计 1.1 数据库名: forum db 1.2 表的设计 1.3 编写SQL 2.系统设计 2.1 技术选型 2.2 设计数据库结构 2.2.1 数据库实体 通过需求分析获得概念类并结合业务实现过程中的技术需要&#x…...

DeepSeek越强,Kimi越慌?
被DeepSeek吊打的Kimi,还有多少人在用? 去年,月之暗面创始人杨植麟别提有多风光了。90后清华学霸,国产大模型六小虎之一,手握十几亿美金的融资。旗下的AI助手Kimi烧钱如流水,单月光是投流就花费2个亿。 疯…...
