强化学习的数学原理学习笔记 - RL基础知识
文章目录
- Roadmap
- 🟡基础概念
- 贝尔曼方程(Bellman Equation)
- 基本形式
- 矩阵-向量形式
- 迭代求解
- 状态值 vs. 动作值
- 🟡贝尔曼最优方程(Bellman Optimality Equation,BOE)
- 基本形式
- 迭代求解
本系列文章介绍强化学习基础知识与经典算法原理,大部分内容来自西湖大学赵世钰老师的强化学习的数学原理课程(参考资料1),并参考了部分参考资料2、3的内容进行补充。
系列博文索引:
- 强化学习的数学原理学习笔记 - RL基础知识
- 强化学习的数学原理学习笔记 - 基于模型(Model-based)
- 强化学习的数学原理学习笔记 - 蒙特卡洛方法(Monte Carlo)
- 强化学习的数学原理学习笔记 - 时序差分学习(Temporal Difference)
- 强化学习的数学原理学习笔记 - 值函数近似(Value Function Approximation)
- 强化学习的数学原理学习笔记 - 策略梯度(Policy Gradient)
- 强化学习的数学原理学习笔记 - Actor-Critic
参考资料:
- 【强化学习的数学原理】课程:从零开始到透彻理解(完结)(主要)
- Sutton & Barto Book: Reinforcement Learning: An Introduction
- 机器学习笔记
*注:【】内文字为个人想法,不一定准确
Roadmap
*图源:https://github.com/MathFoundationRL/Book-Mathmatical-Foundation-of-Reinforcement-Learning
🟡基础概念
MDP概念:
- 状态(state)、动作(action)、奖励(reward)
- 状态转移概率: p ( s ′ ∣ s , a ) p(s'|s, a) p(s′∣s,a)
- 奖励概率: p ( r ∣ s , a ) p(r|s, a) p(r∣s,a)
马尔可夫性质:与历史无关(memoryless)
其他概念:轨迹(trajectory)、episode / trail、确定性(deterministic)、随机性(stochastic)
| 名称 | 含义 | 形式 | 备注 |
|---|---|---|---|
| 策略(policy) | 从状态映射至所有动作的概率分布 | π ( a ∣ s ) \pi(a | s) π(a∣s):在状态 s s s下选择动作 a a a的概率 | 策略决定了每个状态下应该执行什么样的动作 |
| 期望折扣回报(expected discounted return) | 略 *reward和return的区别:reward指单步的奖励,return指多步的折扣回报 | G t = R t + 1 + γ R t + 2 + γ 2 R t + 3 + ⋯ = ∑ t = 0 ∞ γ t R t + k + 1 G_t = R_{t+1} + \gamma R_{t+2} + \gamma^2 R_{t+3} + \cdots = \sum_{t=0}^{\infty} \gamma^t R_{t+k+1} Gt=Rt+1+γRt+2+γ2Rt+3+⋯=∑t=0∞γtRt+k+1 - γ ∈ [ 0 , 1 ] \gamma \in [0, 1] γ∈[0,1]:折扣因子 - 习惯性写成 R t + 1 R_{t+1} Rt+1,而非 R t R_t Rt | 评估某个策略的好坏,针对单个trajectory |
| 值函数 / 状态值函数(state-value function) | 从状态 s s s开始遵循策略 π \pi π取得的预期总回报(均值) | v π ( s ) = E π [ G t ∣ S t = s ] v_{\pi}(s) = \mathbb{E}_\pi [ G_t | S_t = s ] vπ(s)=Eπ[Gt∣St=s]:策略 π \pi π的状态-值函数 | 评估某个状态本身的价值,进而反映对应策略的价值 |
| Q函数 / 动作值函数(action-value function) | 从状态 s s s开始采取动作 a a a,之后遵循策略 π \pi π取得的预期总回报(均值) | q π ( s , a ) = E π [ G t ∣ S t = s , A t = a ] q_{\pi}(s, a) = \mathbb{E}_\pi [ G_t | S_t = s, A_t = a ] qπ(s,a)=Eπ[Gt∣St=s,At=a]:策略 π \pi π的动作-值函数 | 评估某个状态下特定动作的价值,注意动作 a a a可以不遵循策略 π \pi π |
贝尔曼方程(Bellman Equation)
基本形式
每个状态 S t S_t St的值函数,实际上等于按照策略 π \pi π行动后的奖励( R t + 1 R_{t+1} Rt+1)加上后一个状态 S t + 1 S_{t+1} St+1的值函数的折扣值( γ G t + 1 \gamma G_{t+1} γGt+1),也就是即时奖励(immediate reward)和未来奖励(future rewards)的和。这种思想叫做Bootstrapping(自举法),对应的公式就是贝尔曼方程:
v π ( s ) = E [ R t + 1 + γ G t + 1 ∣ S t = s ] = ∑ a π ( a ∣ s ) ∑ s ′ , r p ( s ′ , r ∣ s , a ) [ r + γ v π ( s ′ ) ] , ∀ s ∈ S \begin{aligned} v_\pi(s) &= \mathbb{E}[R_{t+1} + \gamma G_{t+1} | S_t =s] \\ &= \sum_a \pi (a|s) \sum_{s', r} p(s', r|s, a) [r + \gamma v_\pi(s')], \quad \forall s\in \mathcal {S} \end{aligned} vπ(s)=E[Rt+1+γGt+1∣St=s]=a∑π(a∣s)s′,r∑p(s′,r∣s,a)[r+γvπ(s′)],∀s∈S
贝尔曼方程描述了不同状态之间的值函数的关系。给定策略后求解贝尔曼方程的过程 也称之为策略评估(Policy Evaluation)。
比如有两个策略 π 1 \pi_1 π1和 π 2 \pi_2 π2,如果对于任何 s ∈ S s\in \mathcal {S} s∈S, v π 1 ( s ) ≥ v π 2 ( s ) v_{\pi_1} (s) \geq v_{\pi_2} (s) vπ1(s)≥vπ2(s)都成立,那么可以认为 π 1 \pi_1 π1优于 π 2 \pi_2 π2。
矩阵-向量形式
贝尔曼方程也可以转化为矩阵-向量形式:
v π = r π + γ P π v π v_\pi = r_\pi + \gamma P_\pi v_\pi vπ=rπ+γPπvπ
- 状态向量: v π = [ v π ( s 1 ) , ⋯ , v π ( s n ) ] T ∈ R n v_\pi = [v_\pi(s_1), \cdots, v_\pi(s_n)]^T \in \mathbb{R}^n vπ=[vπ(s1),⋯,vπ(sn)]T∈Rn
- 奖励向量: r π = [ r π ( s 1 ) , ⋯ , r π ( s n ) ] T ∈ R n r_\pi = [r_\pi(s_1), \cdots, r_\pi(s_n)]^T \in \mathbb{R}^n rπ=[rπ(s1),⋯,rπ(sn)]T∈Rn
- 状态转移矩阵: P π ∈ R n × n P_\pi \in \mathbb{R}^{n\times n} Pπ∈Rn×n,其中 [ P π ] i j = p π ( s j ∣ s i ) [P_\pi]_{ij} = p_\pi (s_j|s_i) [Pπ]ij=pπ(sj∣si)
*四个状态时的示例:
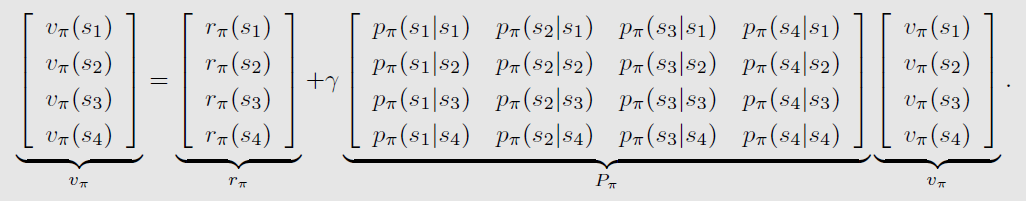
迭代求解
v k + 1 = r π + γ P π v k v_{k+1} = r_\pi + \gamma P_\pi v_k vk+1=rπ+γPπvk
先假设一个 v k v_k vk的值,基于该值计算出 v k + 1 v_{k+1} vk+1,进而重复该过程不断计算出 v k + 2 , v k + 3 , ⋯ v_{k+2}, v_{k+3}, \cdots vk+2,vk+3,⋯。
可以证明,当 k → ∞ k \rarr \infin k→∞时, v k v_k vk会收敛到 v π v_\pi vπ。
状态值 vs. 动作值
v π ( s ) = ∑ a π ( a ∣ s ) q π ( s , a ) v_\pi (s) = \sum_a \pi (a | s) q_\pi (s, a) vπ(s)=∑aπ(a∣s)qπ(s,a)
状态值可以看作是策略 π \pi π的每个动作值的加权平均。
q π ( s , a ) = ∑ s ′ , r p ( s ′ , r ∣ s , a ) [ r + γ v π ( s ′ ) ] q_\pi (s,a) = \sum_{s', r} p(s', r|s, a) [r + \gamma v_\pi(s')] qπ(s,a)=∑s′,rp(s′,r∣s,a)[r+γvπ(s′)]
动作值可以通过状态值求解,也可以不依赖于状态值求解。
🟡贝尔曼最优方程(Bellman Optimality Equation,BOE)
RL的目标是最大化累计奖励,则必然存在至少一个最优策略,记作 π ∗ \pi_* π∗,其对任意策略 π \pi π都满足: v π ∗ ( s ) ≥ v π ( s ) , ∀ s ∈ S v_{\pi_*} (s) \geq v_{\pi}(s), \forall s\in \mathcal{S} vπ∗(s)≥vπ(s),∀s∈S。
基本形式
最优策略共享相同的最优状态值 v ∗ v_* v∗与最优动作值 a ∗ a_* a∗。寻找最优策略相当于求贝尔曼方程( v π v_\pi vπ、 a π a_\pi aπ)的最优解( max π \max_\pi maxπ),则贝尔曼最优方程为:
v ∗ ( s ) = max π v π ( s ) = max π ∑ a π ( a ∣ s ) q π ( s , a ) \begin{aligned} v_*(s) &= \max_{\pi} v_{\pi}(s) \\ &= \max_{\pi} \sum_a \pi (a | s) q_\pi (s, a) \end{aligned} v∗(s)=πmaxvπ(s)=πmaxa∑π(a∣s)qπ(s,a)
q ∗ ( s , a ) = max π q π ( s , a ) = ∑ s ′ , r p ( s ′ , r ∣ s , a ) [ r + γ v ∗ ( s ′ ) ] \begin{aligned} q_*(s, a) &= \max_{\pi} q_{\pi}(s, a) \\ &= \sum_{s',r} p(s', r|s, a) [r + \gamma v_* (s')] \end{aligned} q∗(s,a)=πmaxqπ(s,a)=s′,r∑p(s′,r∣s,a)[r+γv∗(s′)]
对应的矩阵-向量形式:
v = max π ( r π + γ P π v ) v = \max_\pi (r_\pi+\gamma P_\pi v) v=maxπ(rπ+γPπv)
贝尔曼最优方程是一个特殊的贝尔曼方程,即当策略 π \pi π为最优策略 π ∗ \pi_* π∗时的贝尔曼方程:
π ∗ = arg max π ( r π + γ P π v ∗ ) \pi_* = \argmax_\pi (r_\pi + \gamma P_\pi v_*) π∗=argmaxπ(rπ+γPπv∗)
v ∗ = ( r π ∗ + γ P π ∗ v ∗ ) v_* = (r_{\pi_*}+\gamma P_{\pi_*} v_*) v∗=(rπ∗+γPπ∗v∗)
注意:
- 最优状态值唯一,但最优策略并不唯一
- 对于一个给定系统,其最优状态值和最优策略受奖励值 r r r与折扣因子 γ \gamma γ的影响
- 最优策略不受奖励值的绝对大小影响,但受其相对大小影响
- 折扣因子越小(接近0),策略越短视,反之(接近1)策略越长远
迭代求解
考虑贝尔曼最优方程的矩阵-向量形式,设 f ( v ) = max π ( r π + γ P π v ) f(v) = \max_\pi (r_\pi+\gamma P_\pi v) f(v)=maxπ(rπ+γPπv),则贝尔曼最优方程可以写作: v = f ( v ) v = f(v) v=f(v)。
- 其中 f ( v ) f(v) f(v)为向量, [ f ( v ) ] s = max π ∑ a π ( a ∣ s ) q ( s , a ) , ∀ s ∈ S [f(v)]_s = \max_\pi \sum_a \pi(a|s)q(s, a), \quad\forall s\in\mathcal{S} [f(v)]s=maxπ∑aπ(a∣s)q(s,a),∀s∈S
基于压缩映射定理(contraction mapping theorem)可知, v = f ( v ) v = f(v) v=f(v)的解(即最优状态值 v ∗ v_* v∗)存在且唯一。可以通过迭代的方式进行求解,即:
v k + 1 = max π ( r π + γ P π v k ) v_{k+1} = \max_\pi (r_\pi+\gamma P_\pi v_k) vk+1=maxπ(rπ+γPπvk),其中 k = 0 , 1 , 2 , ⋯ k=0, 1,2,\cdots k=0,1,2,⋯
可以证明,当 k → ∞ k\rarr \infin k→∞时, v k → v ∗ v_k\rarr v_* vk→v∗。
通常的求解流程:【实际上就是基于模型(Model-based)中的值迭代(Value Iteration)算法】
- 对于任意一个状态 s ∈ S s\in\mathcal{S} s∈S,估计当前的状态值为 v k ( s ) v_k(s) vk(s)
- 对于任意一个动作 a ∈ A ( s ) a\in\mathcal{A}(s) a∈A(s),计算 q k ( s , a ) = ∑ s ′ , r p ( s ′ , r ∣ s , a ) [ r + γ v k ( s ′ ) ] q_k(s,a) = \sum_{s',r} p(s', r|s, a) [r + \gamma v_k (s')] qk(s,a)=∑s′,rp(s′,r∣s,a)[r+γvk(s′)]
- v k ( s ′ ) v_k (s') vk(s′)在第一次迭代时取初始值,后续迭代时使用前一轮迭代中更新后的值
- 计算状态s下的确定性贪婪策略 π k + 1 ( a ∣ s ) = { 1 a = a k ∗ ( s ) 0 a ≠ a k ∗ ( s ) \pi_{k+1}(a|s) = \begin{cases} 1 &a = a_k^*(s) \\ 0 &a \neq a_k^*(s) \end{cases} πk+1(a∣s)={10a=ak∗(s)a=ak∗(s)
- a k ∗ ( s ) = arg max a q k ( s , a ) a_k^*(s) = \argmax_a q_k(s, a) ak∗(s)=argmaxaqk(s,a),表示使得当前状态动作值最大的那个动作
- 计算 v k + 1 ( s ) = max a q k ( s , a ) v_{k+1}(s) = \max_a q_k (s, a) vk+1(s)=maxaqk(s,a),继续下一轮迭代
- v k + 1 ( s ) v_{k+1}(s) vk+1(s)实际上就是上一步的最优动作对应的动作值(因为当前策略下其他动作的概率均为0)
在实际应用中,当 ∥ v k + 1 ( s ) − v k ( s ) ∥ \|v_{k+1}(s) -v_{k}(s)\| ∥vk+1(s)−vk(s)∥低于某个阈值(如0.001)之后,就可以认为算法收敛了。
由于精确求解贝尔曼方程往往需要极高的计算开销,所以通常只获得近似解即可。
压缩映射定理(contraction mapping theorem),又称巴拿赫不动点定理(Banach fixed-point theorem)
参考:
- 非常神奇的数学结论有哪些? - 知乎
- Chapter 3: The Contraction Mapping Theorem - UC Davis Math
- 巴拿赫不动点定理 - 维基百科
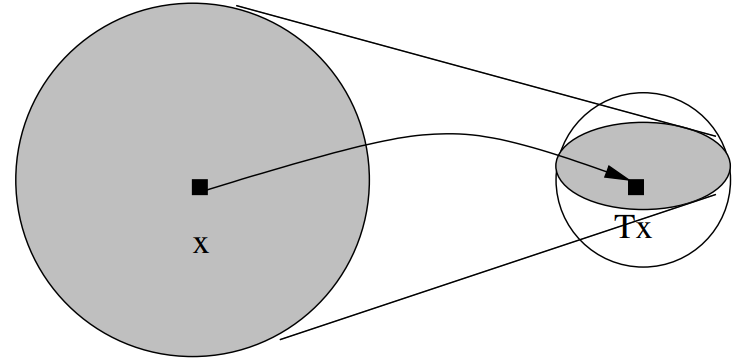
直观认识:
将世界地图放在一个桌子上,则该桌子上必有一点,其实际位置会和地图上该点的对应位置重合,该点称之为“不动点(fixed point)”。
将该点的实际位置视作变量 x x x,其在地图上的位置视作函数 f ( x ) f(x) f(x),则 f ( x ) f(x) f(x)可以视作对于 x x x的一种“压缩映射”, f ( x ) = x f(x)=x f(x)=x的解即为不动点。
数学描述:
若 ∥ f ( x 1 ) − f ( x 2 ) ∥ ≤ γ ∥ x 1 − x 2 ∥ \|f(x_1)-f(x_2)\| \leq \gamma\| x_1 - x_2 \| ∥f(x1)−f(x2)∥≤γ∥x1−x2∥(其中 γ ∈ ( 0 , 1 ) \gamma\in (0, 1) γ∈(0,1)),则 f f f为关于 x x x的压缩映射。
- 此处 f ( x ) f(x) f(x)与 x x x均为向量, ∥ ⋅ ∥ \|\cdot\| ∥⋅∥为向量范数(vector norm)
- 例如: f ( x ) = 0.5 x f(x) = 0.5x f(x)=0.5x,取 γ = 0.6 \gamma=0.6 γ=0.6则上式成立。
压缩映射定理是指,若 f f f为压缩映射,则必然存在(exist)一个不动点 x ∗ x^* x∗使得 f ( x ∗ ) = x ∗ f(x^*)=x^* f(x∗)=x∗,且 x ∗ x^* x∗唯一(unique)。
求解算法:迭代式算法
对于迭代序列 x k + 1 = f ( x k ) x_{k+1} = f(x_k) xk+1=f(xk),随着 k → ∞ k\rarr\infin k→∞,该序列指数收敛至 x ∗ x^* x∗。
- 例如:以迭代式算法求 f ( x ) = 0.5 x f(x) = 0.5x f(x)=0.5x的不动点,假设 x 0 = 10 x_0=10 x0=10,则可迭代得到: x 1 = 5 , x 2 = 2.5 , x 3 = 1.25 , ⋯ x_1=5, x_2=2.5, x_3=1.25, \cdots x1=5,x2=2.5,x3=1.25,⋯,最终会逼近于0。
相关文章:
强化学习的数学原理学习笔记 - RL基础知识
文章目录 Roadmap🟡基础概念贝尔曼方程(Bellman Equation)基本形式矩阵-向量形式迭代求解状态值 vs. 动作值 🟡贝尔曼最优方程(Bellman Optimality Equation,BOE)基本形式迭代求解 本系列文章介…...

winSCP是什么?它有什么功能和特性?它值不值得我们去学习?我们该如何去学习呢?
WinSCP是一款免费的开源SFTP、SCP、FTP和WebDAV客户端,用于Windows操作系统。它提供了一个图形化界面,使用户可以方便地在本地计算机和远程计算机之间传输文件。 WinSCP支持SSH加密通信和多种认证方法,包括密码、公钥和键盘交互。它还支持自…...

SpringBoot的数据层解决方案
🙈作者简介:练习时长两年半的Java up主 🙉个人主页:程序员老茶 🙊 ps:点赞👍是免费的,却可以让写博客的作者开心好久好久😎 📚系列专栏:Java全栈,…...

极客时间-《如何成为学习高手》文章笔记 + 个人思考
极客时间-《如何成为学习高手》文章笔记 个人思考 底层思维高效学习05|教你全面提升专注力,学习时不再走神06|教你高效复习:巧用学习神器取得好成绩07|我考北大中文系时,15 天背下 10 门专业课的连点成线法…...

【前端】下载文件方法
1.window.open 我最初使用的方法就是这个,只要提供了文件的服务器地址,使用window.open也就是在新窗口打开,这时浏览器会自动执行下载。 2.a标签 其实window.open和a标签是一样的,只是a标签是要用户点击触发,而wind…...
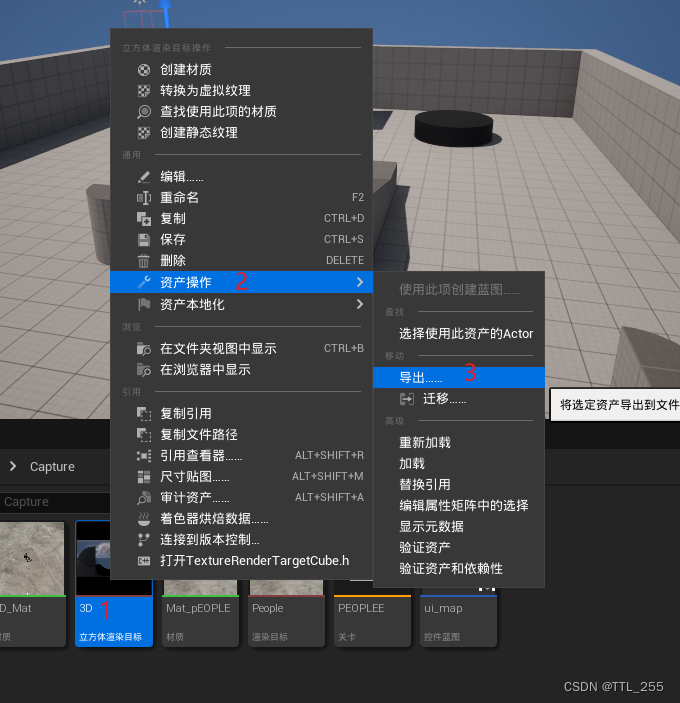
虚幻UE 材质-纹理 1
本篇笔记主要讲两个纹理内的内容:渲染目标和媒体纹理 媒体纹理可以参考之前的笔记:虚幻UE 媒体播放器-视频转成材质-播放视频 所以本篇主要讲两个组件:场景捕获2D、场景捕获立方体 两个纹理:渲染目标、立方体渲染目标 三个功能&am…...

回归预测 | Matlab实现RIME-HKELM霜冰算法优化混合核极限学习机多变量回归预测
回归预测 | Matlab实现RIME-HKELM霜冰算法优化混合核极限学习机多变量回归预测 目录 回归预测 | Matlab实现RIME-HKELM霜冰算法优化混合核极限学习机多变量回归预测效果一览基本介绍程序设计参考资料 效果一览 基本介绍 1.Matlab实现RIME-HKELM霜冰算法优化混合核极限学习机多变…...

【AWS系列】巧用 G5g 畅游Android流媒体游戏
序言 Amazon EC2 G5g 实例由 AWS Graviton2 处理器提供支持,并配备 NVIDIA T4G Tensor Core GPU,可为 Android 游戏流媒体等图形工作负载提供 Amazon EC2 中最佳的性价比。它们是第一个具有 GPU 加速功能的基于 Arm 的实例。 借助 G5g 实例,游…...
)
GNSS数据及产品下载地址(FTP/HTTP)
GNSS数据/产品下载地址 天线改正文件(atx)下载Index of /pub/station/general 通用广播星历(brdc/brdm):ftp://cddis.gsfc.nasa.gov/pub/gps/data/daily/YYYY/brdcftp://cddis.gsfc.nasa.gov/pub/gps/data/campaign/mgex/daily/rinex3/YYYY/brdmftp://epncb.oma.b…...

【STM32】STM32学习笔记-DMA数据转运+AD多通道(24)
00. 目录 文章目录 00. 目录01. DMA简介02. DMA相关API2.1 DMA_Init2.2 DMA_InitTypeDef2.3 DMA_Cmd2.4 DMA_SetCurrDataCounter2.5 DMA_GetFlagStatus2.6 DMA_ClearFlag 03. DMA数据单通道接线图04. DMA数据单通道示例05. DMA数据多通道接线图06. DMA数据多通道示例一07. DMA数…...
即时设计:设计流程图,让您的设计稿更具条理和逻辑
流程图小助手 更多内容 在设计工作中,流程图是一种重要的工具,它可以帮助设计师清晰地展示设计思路和流程,提升设计的条理性和逻辑性。今天,我们要向您推荐一款强大的设计工具,它可以帮助您轻松为设计稿设计流程图&a…...

单个独立按键控制直流电机开关
/*----------------------------------------------- 内容:对应的电机接口需用杜邦线连接到uln2003电机控制端 使用5V-12V 小功率电机皆可 ------------------------------------------------*/ #include<reg52.h> //包含头文件,一般情况…...

前端插件库-VUE3 使用 JSEncrypt 插件
JSEncrypt 是一个用于在客户端进行加密的 JavaScript 库。它基于 RSA 加密算法,可以用于在浏览器中对数据进行加密和解密操作。 以下是使用 JSEncrypt 进行加密和解密的基本示例: 第一步:安装 JSEncrypt 首先,你需要引入 JSEn…...
Neo4j备份
这里主要讲Neo4j在windows环境下如何备份,Linux环境同理 Neo4j恢复看这里:Neo4j恢复-CSDN博客 Step1:停服 关闭neo4j.bat console会话窗口即可 Step2: 备份 找到数据目录,并备份、压缩 copy即可 data - 20240108.7z Step3: 启动服务 进入命令行&am…...

【LangChain学习之旅】—(5) 提示工程(上):用少样本FewShotTemplate和ExampleSelector创建应景文案
【LangChain学习之旅】—(5) 提示工程(上):用少样本FewShotTemplate和ExampleSelector创建应景文案 提示的结构LangChain 提示模板的类型使用 PromptTemplate使用 ChatPromptTemplateFewShot 的思想起源使用 FewShotPr…...

Python从入门到精通秘籍一
Python速成,知识点超详细,跟着这个系列边输入边学习体会吧! 一、字面量 下面是一些使用代码示例来说明Python的字面量的具体用法: 1.数字字面量: integer_literal = 42 # 整数字面量 float_literal = 3.14 # 浮点数字面量 complex_literal = 2 + 3j # 复数字面量# …...

【IC设计】移位寄存器
目录 理论讲解背景介绍什么是移位寄存器按工作模式分类verilog语法注意事项 设计实例循环移位寄存器算术双向移位寄存器5位线性反馈移位寄存器伪随机码发生器3位线性反馈移位寄存器32位线性反馈移位寄存器串行移位寄存器(打4拍)双向移位寄存器࿱…...

【Flutter 开发实战】Dart 基础篇:最基本的语法内容
在深入了解 Dart 这门编程语言之前,我们需要了解一些关于 Dart 的最基本的知识,像是常量、变量、函数等等,这样才能够让我们的开发效率更上一层楼。在本节,我们将探讨一些基础语法,包括入口方法 main、变量、常量以及命…...

中国光伏展
中国光伏展是中国最大的光伏产业展览会,每年在国内举办一次。该展览会汇集了国内外光伏行业的领先企业和专业人士,展示最新的光伏技术、产品和解决方案。 中国光伏展旨在促进光伏行业的发展和创新,提升光伏产业的国际竞争力。展览会涵盖了光伏…...
Nacos的统一配置管理
Nacos的统一配置管理 一 项目添加nacos和bootstrap依赖二 nacos客户端配置2.1 创建命名空间2.2 创建配置 三、配置bootstrap.yml四 不同环境配置切换步骤一:nacos中添加开发、测试配置步骤二:指定bootstrap.yml中spring.profiles.active参数值 扩展链接 …...

Cesium1.95中高性能加载1500个点
一、基本方式: 图标使用.png比.svg性能要好 <template><div id"cesiumContainer"></div><div class"toolbar"><button id"resetButton">重新生成点</button><span id"countDisplay&qu…...

可靠性+灵活性:电力载波技术在楼宇自控中的核心价值
可靠性灵活性:电力载波技术在楼宇自控中的核心价值 在智能楼宇的自动化控制中,电力载波技术(PLC)凭借其独特的优势,正成为构建高效、稳定、灵活系统的核心解决方案。它利用现有电力线路传输数据,无需额外布…...

智能在线客服平台:数字化时代企业连接用户的 AI 中枢
随着互联网技术的飞速发展,消费者期望能够随时随地与企业进行交流。在线客服平台作为连接企业与客户的重要桥梁,不仅优化了客户体验,还提升了企业的服务效率和市场竞争力。本文将探讨在线客服平台的重要性、技术进展、实际应用,并…...

ESP32 I2S音频总线学习笔记(四): INMP441采集音频并实时播放
简介 前面两期文章我们介绍了I2S的读取和写入,一个是通过INMP441麦克风模块采集音频,一个是通过PCM5102A模块播放音频,那如果我们将两者结合起来,将麦克风采集到的音频通过PCM5102A播放,是不是就可以做一个扩音器了呢…...

ServerTrust 并非唯一
NSURLAuthenticationMethodServerTrust 只是 authenticationMethod 的冰山一角 要理解 NSURLAuthenticationMethodServerTrust, 首先要明白它只是 authenticationMethod 的选项之一, 并非唯一 1 先厘清概念 点说明authenticationMethodURLAuthenticationChallenge.protectionS…...

Linux-07 ubuntu 的 chrome 启动不了
文章目录 问题原因解决步骤一、卸载旧版chrome二、重新安装chorme三、启动不了,报错如下四、启动不了,解决如下 总结 问题原因 在应用中可以看到chrome,但是打不开(说明:原来的ubuntu系统出问题了,这个是备用的硬盘&a…...

12.找到字符串中所有字母异位词
🧠 题目解析 题目描述: 给定两个字符串 s 和 p,找出 s 中所有 p 的字母异位词的起始索引。 返回的答案以数组形式表示。 字母异位词定义: 若两个字符串包含的字符种类和出现次数完全相同,顺序无所谓,则互为…...

分布式增量爬虫实现方案
之前我们在讨论的是分布式爬虫如何实现增量爬取。增量爬虫的目标是只爬取新产生或发生变化的页面,避免重复抓取,以节省资源和时间。 在分布式环境下,增量爬虫的实现需要考虑多个爬虫节点之间的协调和去重。 另一种思路:将增量判…...

中医有效性探讨
文章目录 西医是如何发展到以生物化学为药理基础的现代医学?传统医学奠基期(远古 - 17 世纪)近代医学转型期(17 世纪 - 19 世纪末)现代医学成熟期(20世纪至今) 中医的源远流长和一脉相承远古至…...

深度学习水论文:mamba+图像增强
🧀当前视觉领域对高效长序列建模需求激增,对Mamba图像增强这方向的研究自然也逐渐火热。原因在于其高效长程建模,以及动态计算优势,在图像质量提升和细节恢复方面有难以替代的作用。 🧀因此短时间内,就有不…...
