【排序】对各种排序的总结
文章目录
- 前言
- 1. 排序算法的复杂度及稳定性分析
- 2. 排序算法的性能测试
- 2.1 重复率较低的随机值排序测试
- 2.2 重复率较高的随机值排序测试
前言
本篇是基于我这几篇博客做的一个总结:
- 《简单排序》(含:冒泡排序,直接插入排序,选择排序,计数排序)
- 《希尔排序》
- 《堆排序》
- 《快速排序》
- 《归并排序》
我会再对他们的时间复杂度、空间复杂度以及稳定性再做一次总结,并且在不同的场景下,测试他们的性能怎么样。
1. 排序算法的复杂度及稳定性分析
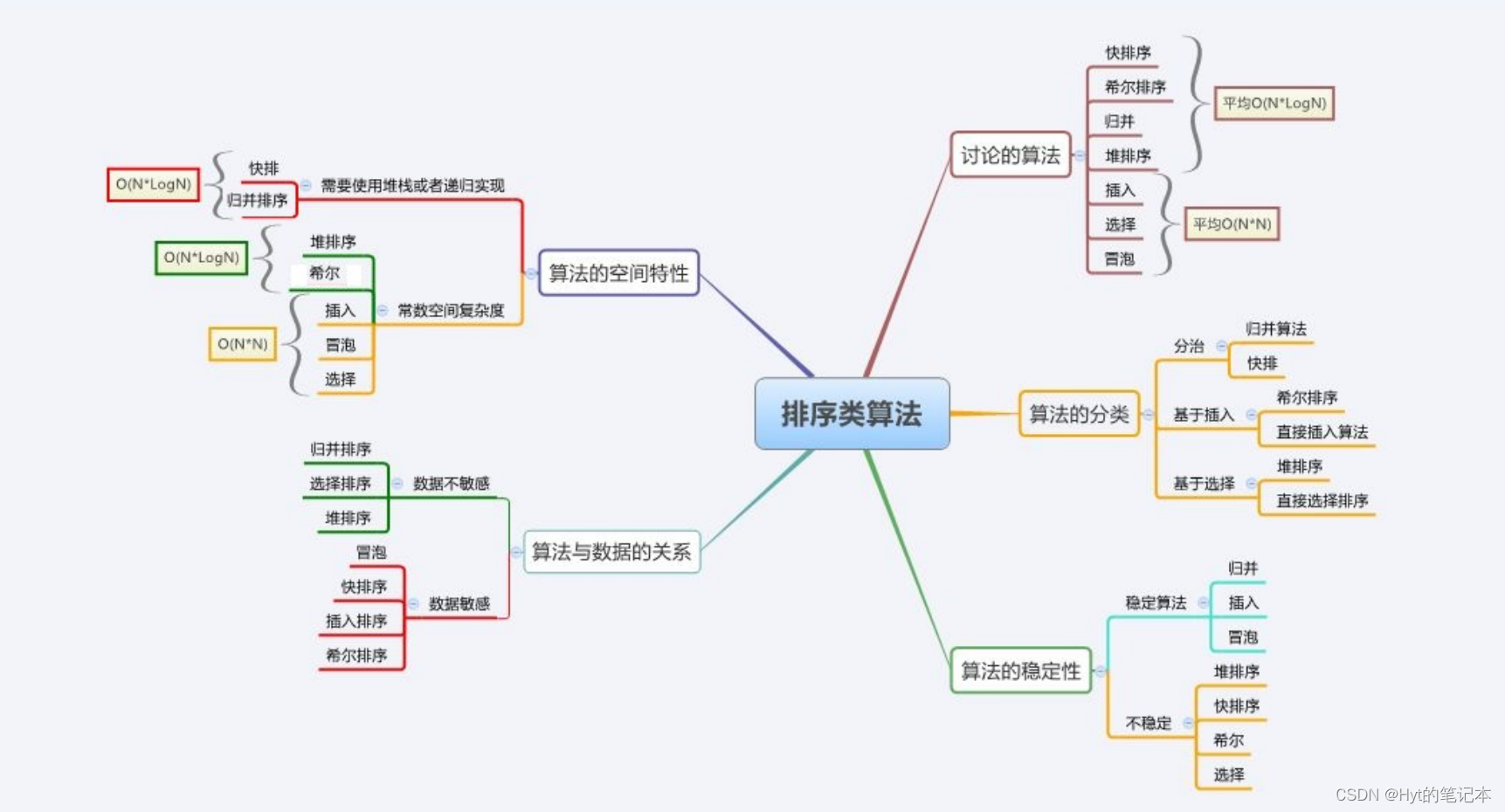
| 排序方法 | 平均情况 | 最好情况 | 最坏情况 | 辅助空间 | 稳定性 |
|---|---|---|---|---|---|
| 冒泡排序 | O O O( N N N2) | O O O( N N N) | O O O( N N N2) | O O O( 1 1 1) | 稳定 |
| 选择排序 | O O O( N N N2) | O O O( N N N2) | O O O( N N N2) | O O O( 1 1 1) | 不稳定 |
| 直接插入排序 | O O O( N N N2) | O O O( N N N) | O O O( N N N2) | O O O( 1 1 1) | 稳定 |
| 计数排序 | O O O( N + r a n g e N+range N+range) | O O O( N N N) | O O O( N + r a n g e N+range N+range) | O O O( r a n g e range range) | — |
| 希尔排序 | O O O( N ∗ l o g N N*logN N∗logN) ~ O O O( N N N2) | O O O( N N N1.3) | O O O( N N N2) | O O O( 1 1 1) | 不稳定 |
| 堆排序 | O O O( N ∗ l o g N N*logN N∗logN) | O O O( N ∗ l o g N N*logN N∗logN) | O O O( N ∗ l o g N N*logN N∗logN) | O O O( 1 1 1) | 不稳定 |
| 归并排序 | O O O( N ∗ l o g N N*logN N∗logN) | O O O( N ∗ l o g N N*logN N∗logN) | O O O( N ∗ l o g N N*logN N∗logN) | O O O( N N N) | 稳定 |
| 快速排序 | O O O( N ∗ l o g N N*logN N∗logN) | O O O( N ∗ l o g N N*logN N∗logN) | O O O( N N N2) | O O O( l o g N logN logN) ~ O O O( N N N) | 不稳定 |
2. 排序算法的性能测试
⚠️:我这里只是测试一遍的结果截图,目的是让大家看看,判断一个排序的优劣需要不同场景下的大量测试。
我们比较排序时,应该换成release版本来测试,这样性能才会全部拉满
先写一段测试代码
// 测试排序的性能对比
// 测试排序的性能对比
void TestOP()
{srand(time(0));const int N = 100000; // 十万个数的比较int* a1 = (int*)malloc(sizeof(int) * N);int* a2 = (int*)malloc(sizeof(int) * N);int* a3 = (int*)malloc(sizeof(int) * N);int* a4 = (int*)malloc(sizeof(int) * N);int* a5 = (int*)malloc(sizeof(int) * N);int* a6 = (int*)malloc(sizeof(int) * N);int* a7 = (int*)malloc(sizeof(int) * N);int* a8 = (int*)malloc(sizeof(int) * N);for (int i = 0; i < N; ++i){a1[i] = rand() + i; // 生成十万个重复率低的随机值//a1[i] = rand() % 100; // 生成十万个重复率高的随机值a2[i] = a1[i];a3[i] = a1[i];a4[i] = a1[i];a5[i] = a1[i];a6[i] = a1[i];a7[i] = a1[i];a8[i] = a1[i];}int begin1 = clock();InsertSort(a1, N);int end1 = clock();int begin2 = clock();SelectSort(a2, N);int end2 = clock();int begin3 = clock();ShellSort(a3, N);int end3 = clock();int begin4 = clock();HeapSort(a4, N);int end4 = clock();int begin5 = clock();QuickSort(a5, 0, N);int end5 = clock();int begin6 = clock();MergeSort(a6, N);int end6 = clock();int begin7 = clock();QuickSortNonR(a7, 0, N);int end7 = clock();int begin8 = clock();MergeSortNonR(a8, N);int end8 = clock();printf("InsertSort:%d\n", end1 - begin1);printf("SelectSort:%d\n", end2 - begin2);printf("ShellSort:%d\n", end3 - begin3);printf("HeapSort:%d\n", end4 - begin4);printf("QuickSort:%d\n", end5 - begin5);printf("MergeSort:%d\n", end6 - begin6);printf("QuickSortNonR:%d\n", end7 - begin7);printf("MergeSortNonR:%d\n", end8 - begin8);free(a1);free(a2);free(a3);free(a4);free(a5);free(a6);
}int main()
{srand((unsigned)time(NULL)); // 生成随机数种子TestOP();return 0;
}
2.1 重复率较低的随机值排序测试
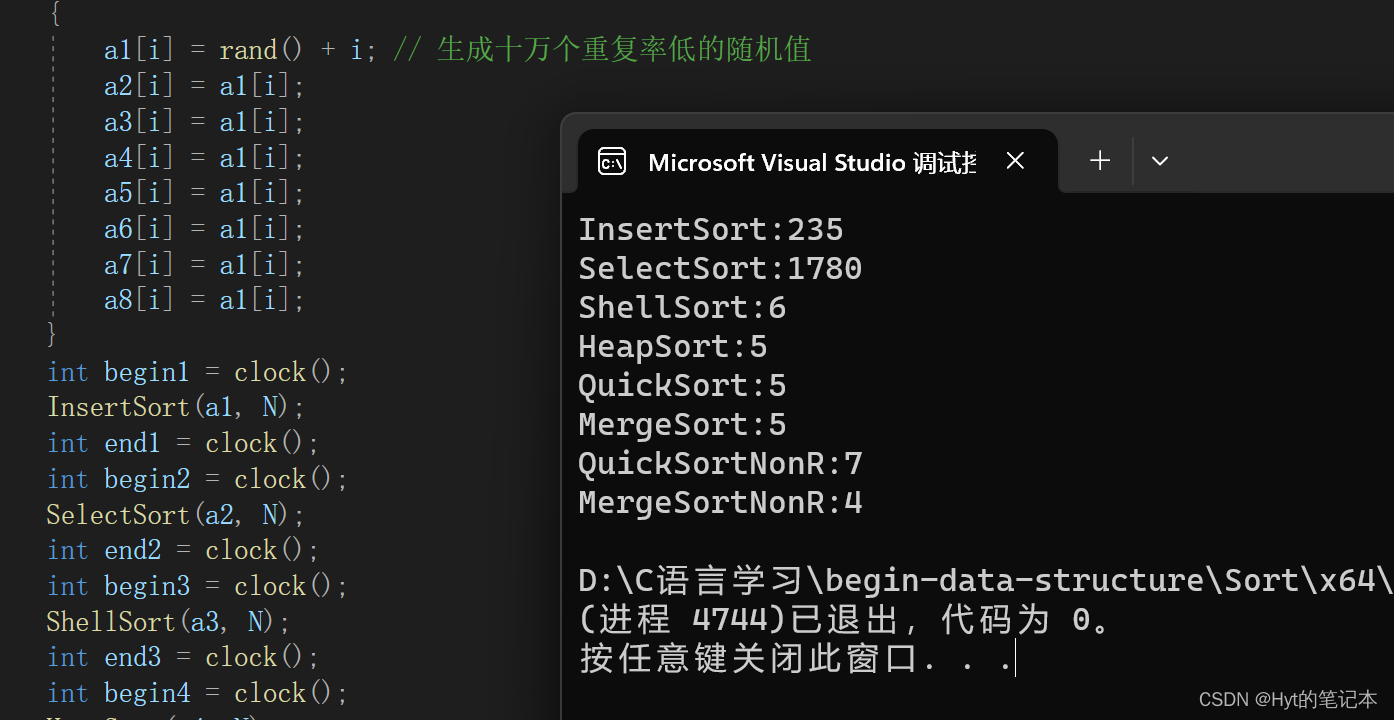
可以看到,直接插入排序在比较低阶的排序算法中,算是很优秀的一个排序了。
我们继续加大数据,但是我得把效率比较低的排序关掉,单独来比那些比较高阶的排序:
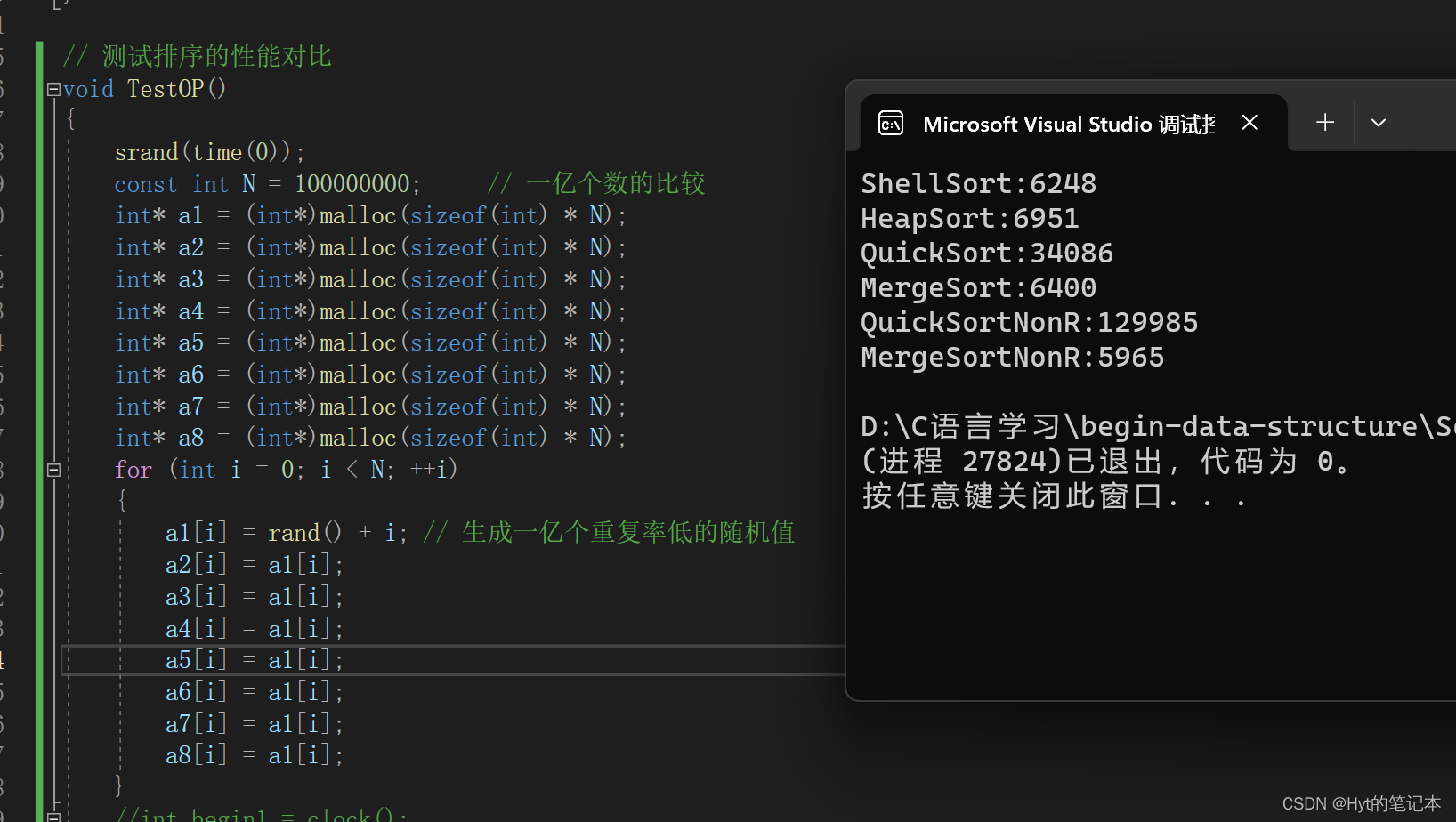
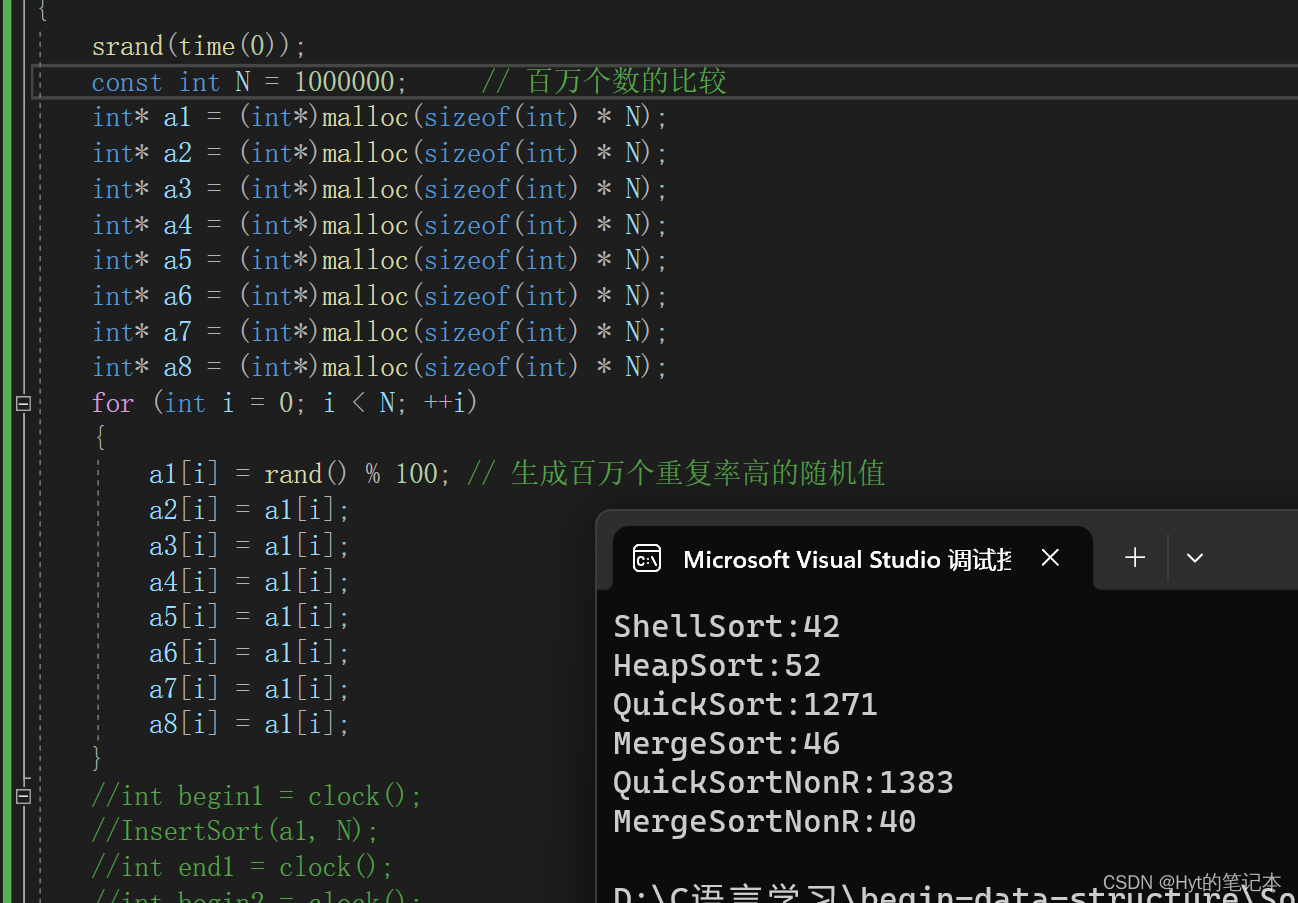
2.2 重复率较高的随机值排序测试
直接看结果:
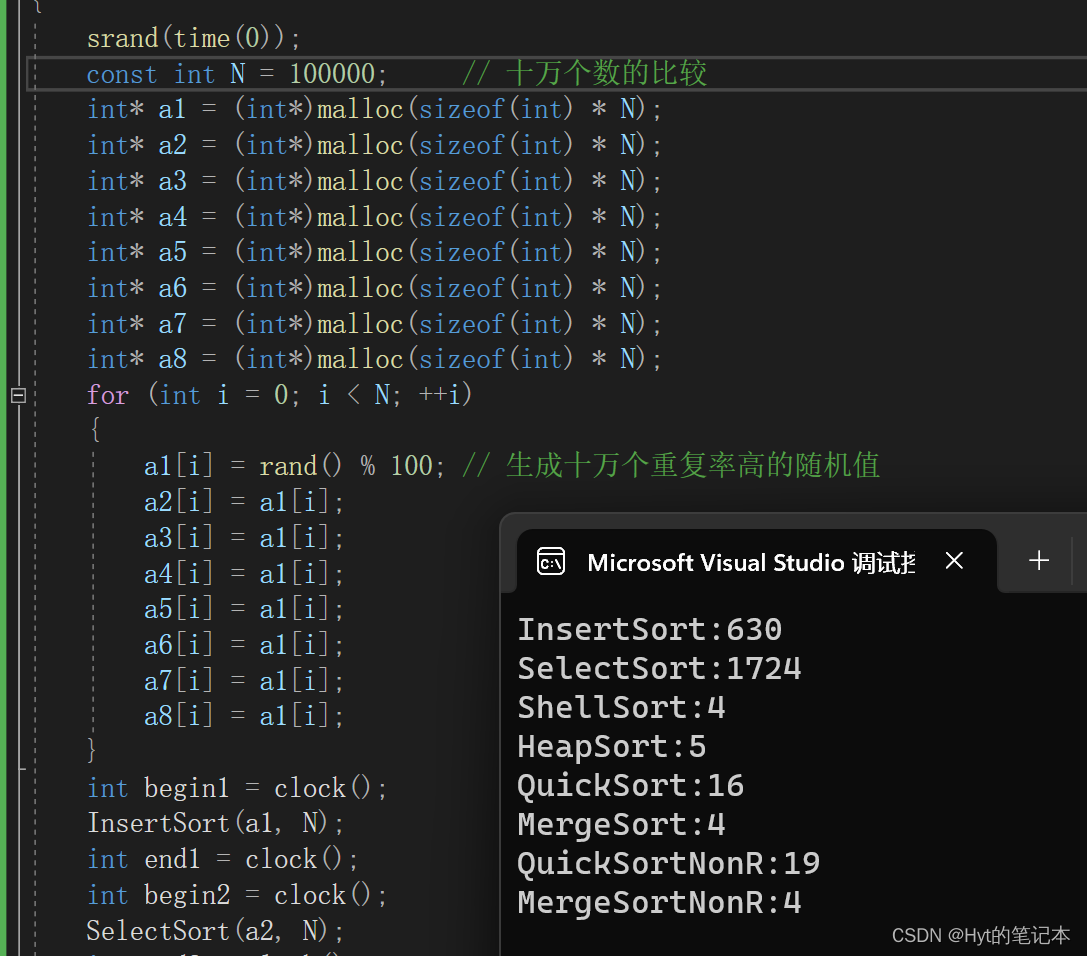
继续加大数据,把效率比较低的排序关掉,单独来比那些比较高阶的排序:
相关文章:

【排序】对各种排序的总结
文章目录 前言1. 排序算法的复杂度及稳定性分析2. 排序算法的性能测试2.1 重复率较低的随机值排序测试2.2 重复率较高的随机值排序测试 前言 本篇是基于我这几篇博客做的一个总结: 《简单排序》(含:冒泡排序,直接插入排序&#x…...
Apache ActiveMQ RCE CNVD-2023-69477 CVE-2023-46604
漏洞简介 Apache ActiveMQ官方发布新版本,修复了一个远程代码执行漏洞,攻击者可构造恶意请求通过Apache ActiveMQ的61616端口发送恶意数据导致远程代码执行,从而完全控制Apache ActiveMQ服务器。 影响版本 Apache ActiveMQ 5.18.0 before …...
C语言可变参数输入
本博文源于笔者正在学习的可变参数输入,可变参数是c语言函数中的一部分,下面本文就以一个很小的demo演示可变参数的编写 问题来源 想要用可变参数进行多个整数相加 方法源码 #include<stdio.h> #include<stdlib.h> #include<stdarg.h…...

飞天使-k8s知识点10-kubernetes资源对象3-controller
文章目录 pod探针 控制器 pod 概述: 1. pod是k8s中的最小单元 2. 一个pod中可以运行一个容器,也可以运行多个容器 3. 运行多个容器的话,这些容器是一起被调度的 4. Pod的生命周期是短暂的,不会自愈,是用完就销毁的实体…...

【Vue技巧】Vue2和Vue3组件上使用v-model的实现原理
ChatGPT4.0国内站点,支持GPT4 Vision 视觉模型:海鲸AI 在Vue中,v-model 是一个语法糖,用于在输入框、选择框等表单元素上创建双向数据绑定。当你在自定义组件中实现 v-model 功能时,你需要理解它背后的原理:…...

博客随手记
随手记...
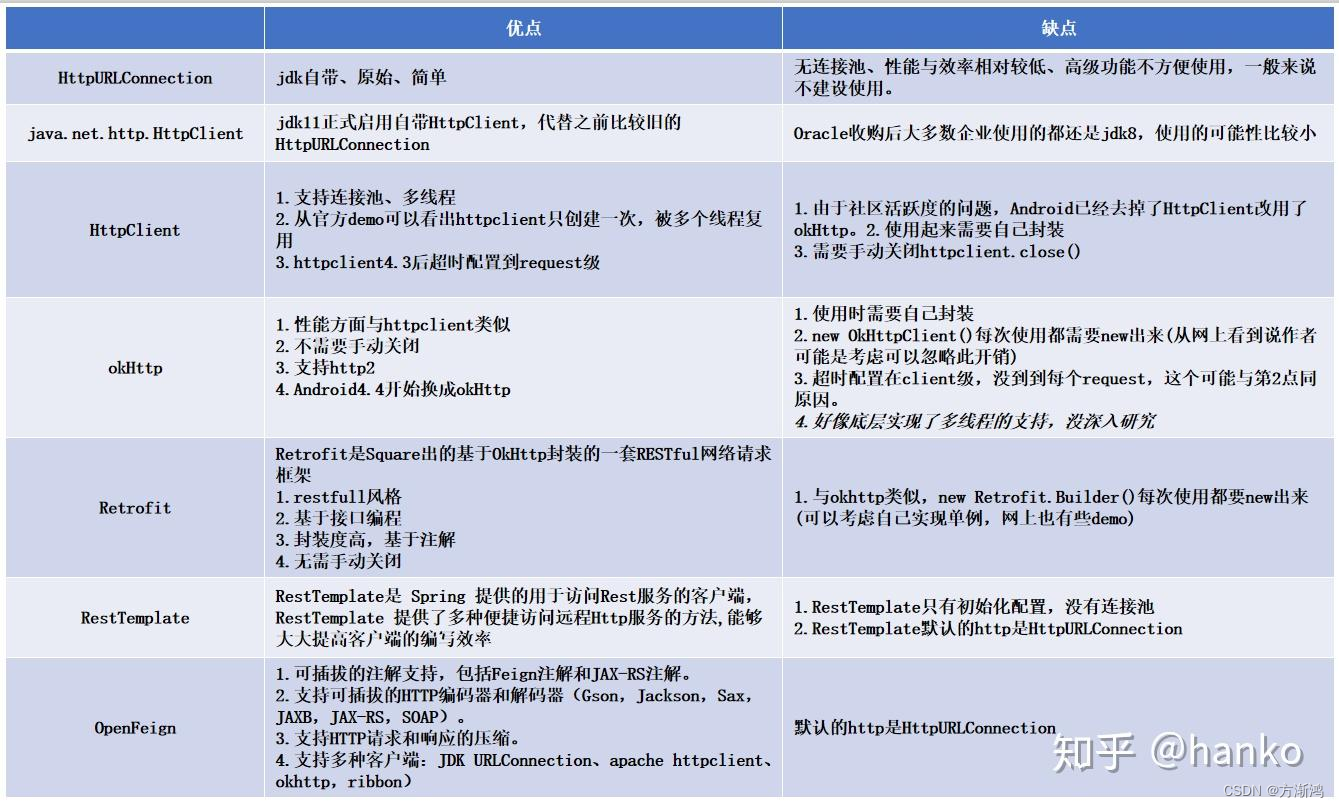
【2023】java常用HTTP客户端对比以及使用(HttpClient/OkHttp/WebClient)
💻目录 1、介绍2、使用2.1、添加配置2.1.1、依赖2.1.2、工具类2.1.3、实体2.1.4、Controller接口 2.2、Apache HttpClient使用2.3 、OkHttp使用2.4、WebClient使用 1、介绍 现在java使用的http客户端主要包括以下几种 而这些中使用得最频繁的主要是: A…...

微信小程序获取来源场景值
https://developers.weixin.qq.com/miniprogram/dev/framework/app-service/scene.html#返回来源信息的场景 https://developers.weixin.qq.com/miniprogram/dev/api/base/app/life-cycle/wx.getLaunchOptionsSync.html 场景值列表 只有1008是来源群聊 /** * 生命周期函数--监…...

Vue3:vue-cli项目创建及vue.config.js配置
一、node.js检测或安装: node -v node.js官方 二、vue-cli安装: npm install -g vue/cli # OR yarn global add vue/cli/*如果安装的时候报错,可以尝试一下方法 删除C:\Users**\AppData\Roaming下的npm和npm-cache文件夹 删除项目下的node…...
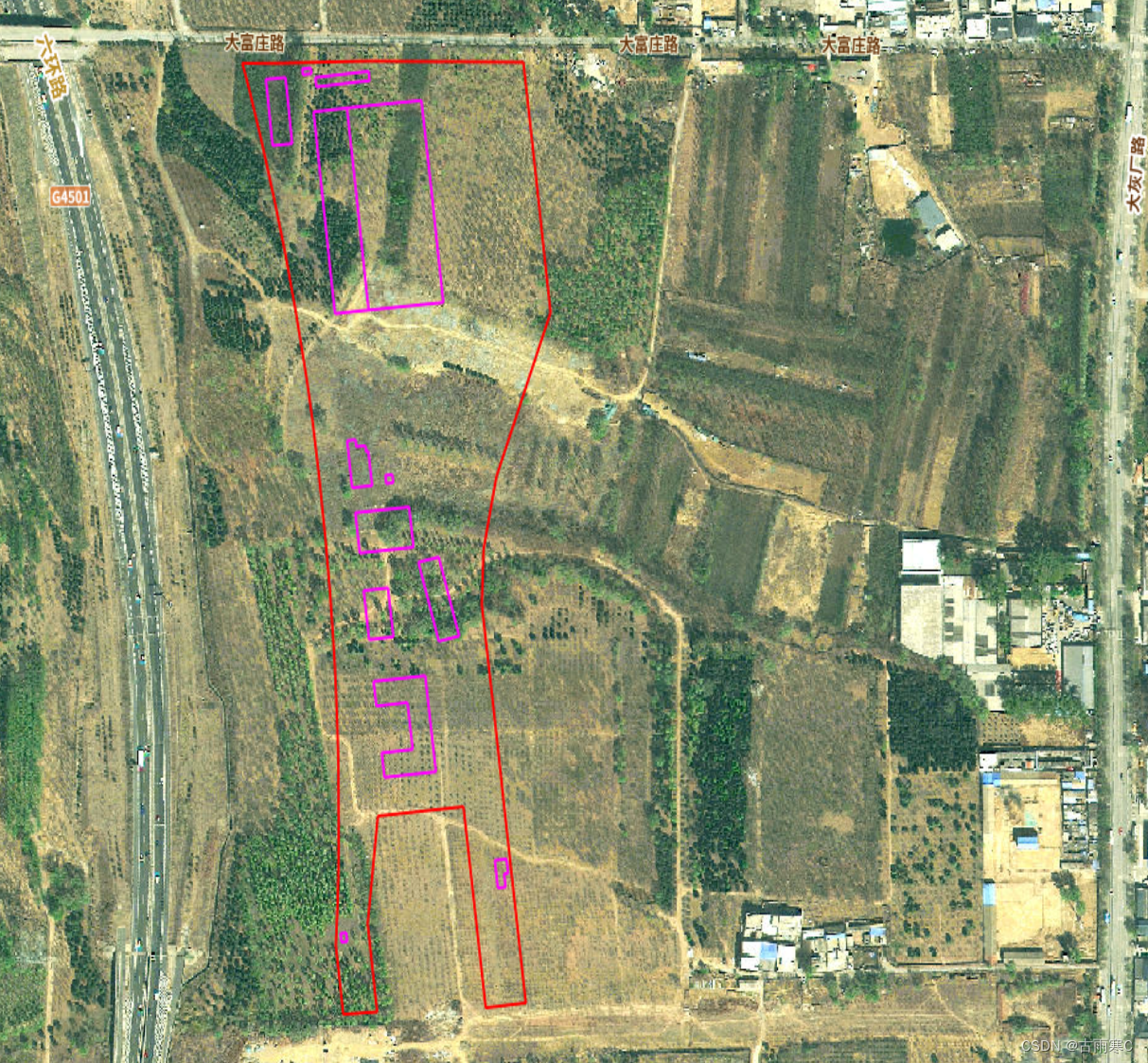
关于CAD导入**地球的一些问题讨论
先上示例: 上图是将北京王佐停车场的红线CAD图导入到图新地球效果,如果看官正是需要这样的效果,那么请你继续往下看,全是干货! 在地球中导入CAD图可以做为电子沙盘。对于工程人来说,是极有帮助的。以前一直用谷歌地球,大约在2020年左右,就被和谐了。当时感觉挺可惜的。…...

Semaphore信号量详解
在Java并发编程中,Semaphore是一个非常重要的工具类。它位于java.util.concurrent包中,为我们提供了一种限制对临界资源的访问的机制。你可以将其视为一个同步控制的瑞士军刀,因为它既能够控制对资源的并发访问数量,也能够保证资源…...

Python的核心知识点整理大全66(已完结撒花)
目录 D.3 忽略文件 .gitignore 注意 D.4 初始化仓库 D.5 检查状态 D.6 将文件加入到仓库中 D.7 执行提交 D.8 查看提交历史 D.9 第二次提交 hello_world.py D.10 撤销修改 hello_world.py 注意 D.11 检出以前的提交 往期快速传送门👆(在文…...
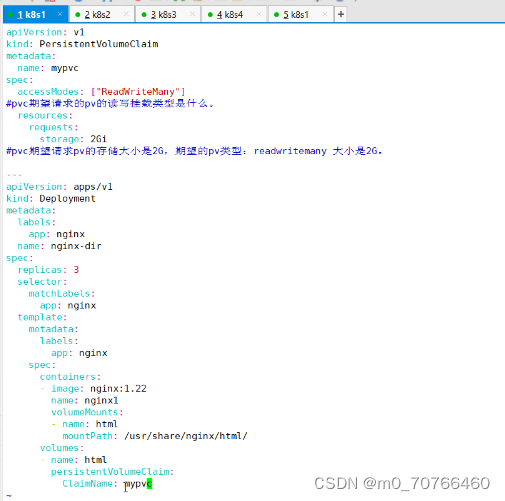
k8s的存储卷
存储卷------数据卷 把容器内的目录,和宿主机的目录进行挂载。 容器在系统上的生命周期是短暂的,delete,k8s用控制(deployment)创建的pod,delete相当于重启,容器的状态也会回复到初始状态。 …...

Git 实战指南:常用指令精要手册(持续更新)
👑专栏内容:Git⛪个人主页:子夜的星的主页💕座右铭:前路未远,步履不停 目录 一、Git 安装过程1、Windows 下安装2、Cent os 下安装3、Ubuntu 下安装 二、配置本地仓库1、 初始化 Git 仓库2、配置 name 和 e…...

关于SpringMVC前后端传值总结
一、传递方式 1、查询参数&路径参数 查询参数: URI:/teachers?typeweb GetMapping("/klasses/teachers") public List<Teacher> getKlassRelatedTeachers(String type ) { ... }如果查询参数type与方法的名称相同,则直接将web传入…...
【排序】归并排序(C语言实现)
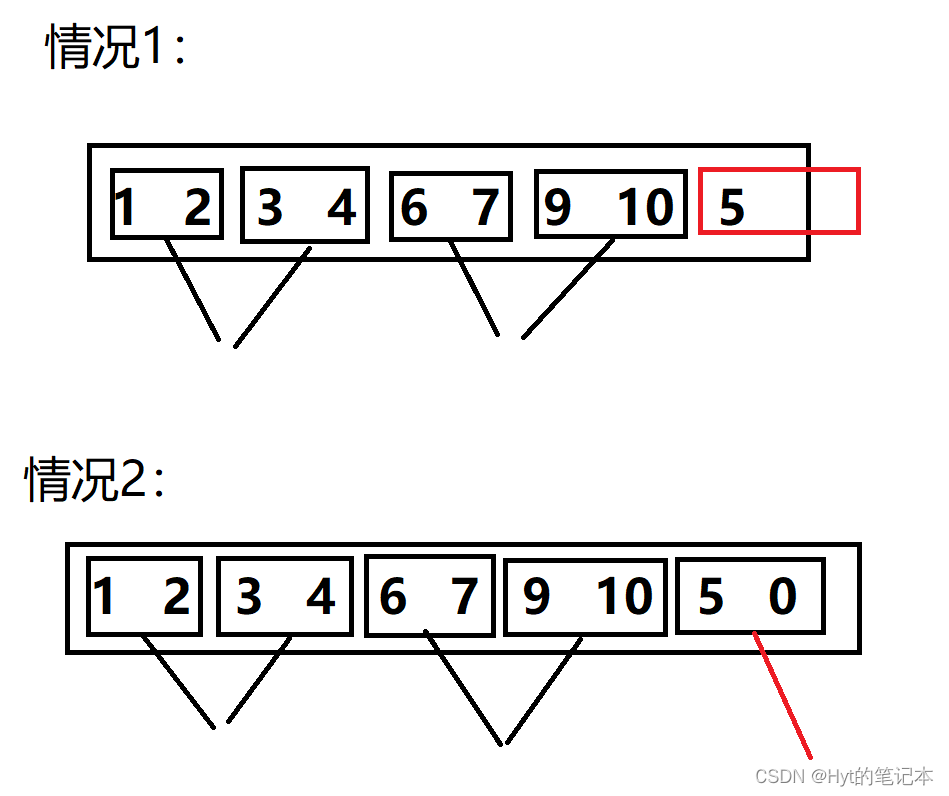
文章目录 1. 递归版的归并排序1.1 归并排序的思想2. 递归版的归并排序的实现 2. 非递归版的归并排序 1. 递归版的归并排序 1.1 归并排序的思想 归并排序(MERGE - SORT)是建立在归并操作上的一种有效的排序算法, 该算法是采用分治法(Divide a…...

127. 单词接龙
和433.最小基因变化这道题一样的解法。 https://blog.csdn.net/qq_43606119/article/details/135538247 class Solution {public int ladderLength(String beginWord, String endWord, List<String> wordList) {Set<String> cnt new HashSet<>();for (int …...

计算机算法贪心算法
贪心算法(Greedy Algorithm)是一种常见的算法思想,它在每一步选择当前状态下最优的解决方案,从而希望最终能够达到全局最优解。 贪心算法的基本思路是每一步都选择当前状态下的局部最优解,而忽略了当前选择所带来的影…...

基于css实现动画效果
介绍 本文将会基于css,实现各种动画效果,接下来会从简单几个例子入手。 案例 三颗球 <!DOCTYPE html> <html lang"en"><head><meta charset"utf-8" /><title>React App</title><style>…...

18.将文件上传至云服务器 + 优化网站的性能
目录 1.将文件上传至云服务器 1.1 处理上传头像逻辑 1.1.1 客户端上传 1.1.2 服务器直传 2.优化网站的性能 2.1 本地缓存优化查询方法 2.2 压力测试 1.将文件上传至云服务器 客户端上传:客户端将数据提交给云服务器,并等待其响应;用户…...

IDEA运行Tomcat出现乱码问题解决汇总
最近正值期末周,有很多同学在写期末Java web作业时,运行tomcat出现乱码问题,经过多次解决与研究,我做了如下整理: 原因: IDEA本身编码与tomcat的编码与Windows编码不同导致,Windows 系统控制台…...
)
rknn优化教程(二)
文章目录 1. 前述2. 三方库的封装2.1 xrepo中的库2.2 xrepo之外的库2.2.1 opencv2.2.2 rknnrt2.2.3 spdlog 3. rknn_engine库 1. 前述 OK,开始写第二篇的内容了。这篇博客主要能写一下: 如何给一些三方库按照xmake方式进行封装,供调用如何按…...

逻辑回归:给不确定性划界的分类大师
想象你是一名医生。面对患者的检查报告(肿瘤大小、血液指标),你需要做出一个**决定性判断**:恶性还是良性?这种“非黑即白”的抉择,正是**逻辑回归(Logistic Regression)** 的战场&a…...

多场景 OkHttpClient 管理器 - Android 网络通信解决方案
下面是一个完整的 Android 实现,展示如何创建和管理多个 OkHttpClient 实例,分别用于长连接、普通 HTTP 请求和文件下载场景。 <?xml version"1.0" encoding"utf-8"?> <LinearLayout xmlns:android"http://schemas…...

Mybatis逆向工程,动态创建实体类、条件扩展类、Mapper接口、Mapper.xml映射文件
今天呢,博主的学习进度也是步入了Java Mybatis 框架,目前正在逐步杨帆旗航。 那么接下来就给大家出一期有关 Mybatis 逆向工程的教学,希望能对大家有所帮助,也特别欢迎大家指点不足之处,小生很乐意接受正确的建议&…...

网络编程(UDP编程)
思维导图 UDP基础编程(单播) 1.流程图 服务器:短信的接收方 创建套接字 (socket)-----------------------------------------》有手机指定网络信息-----------------------------------------------》有号码绑定套接字 (bind)--------------…...

html-<abbr> 缩写或首字母缩略词
定义与作用 <abbr> 标签用于表示缩写或首字母缩略词,它可以帮助用户更好地理解缩写的含义,尤其是对于那些不熟悉该缩写的用户。 title 属性的内容提供了缩写的详细说明。当用户将鼠标悬停在缩写上时,会显示一个提示框。 示例&#x…...
)
Angular微前端架构:Module Federation + ngx-build-plus (Webpack)
以下是一个完整的 Angular 微前端示例,其中使用的是 Module Federation 和 npx-build-plus 实现了主应用(Shell)与子应用(Remote)的集成。 🛠️ 项目结构 angular-mf/ ├── shell-app/ # 主应用&…...

《C++ 模板》
目录 函数模板 类模板 非类型模板参数 模板特化 函数模板特化 类模板的特化 模板,就像一个模具,里面可以将不同类型的材料做成一个形状,其分为函数模板和类模板。 函数模板 函数模板可以简化函数重载的代码。格式:templa…...

基于TurtleBot3在Gazebo地图实现机器人远程控制
1. TurtleBot3环境配置 # 下载TurtleBot3核心包 mkdir -p ~/catkin_ws/src cd ~/catkin_ws/src git clone -b noetic-devel https://github.com/ROBOTIS-GIT/turtlebot3.git git clone -b noetic https://github.com/ROBOTIS-GIT/turtlebot3_msgs.git git clone -b noetic-dev…...
