算法第十二天-矩形区域不超过K的最大数值和
矩形区域不超过K的最大数值和
题目要求


解题思路
来自[宫水三叶]
从题面来看显然是一道[二维前缀和]的题目。本题预处理前缀和的复杂度为O(m* n)
搜索所有子矩阵需要枚举[矩形左上角]和[矩形右下角],复杂度是 O ( m 2 ∗ n 2 ) O(m^2 * n^2) O(m2∗n2),因此,如果把本题当作二维前缀和模板题来做的话,整体复杂度为 O ( m 2 ∗ n 2 ) O(m^2 * n^2) O(m2∗n2).
数据范围是 1 0 2 10^2 102,对应的计算量是 1 0 8 10^8 108,理论上会超时,但当我们枚举[矩形左上角](i,j)的时候,我们只需要搜索位于(i,j)的右下方的点(p,q)作为[矩形右下角],所以其实我们是取不满 m 2 ∗ n 2 m^2 * n^2 m2∗n2的,但是,仍然存在超时风险。
前缀和 & 二分(抽象一维)
我们来细想一下[朴素二维前缀和]解法是如何搜索答案(子矩阵):通过枚举[左上角] & [右下角]来确定某个矩阵
换句话说是通过枚举(i,j)和(p,q)来唯一确定子矩阵的四条边,每个坐标点可以看作确定子矩阵的某条边。
既然要确定的边有四条,我们如何降低复杂呢?
简单的,我们先思考一下同样是枚举的[两数之和]问题
在[两数之和]中可以暴力枚举两个数,也可以只枚举其中一个数,然后使用数据结构(哈希表)来加速找另一个数(这是一个通用的[降低枚举复杂度]思考方向)。
对应到本题,我们可以枚举其中三条边,然后使用数据结构来加速找第四条边。
当我们确定了三条边(红色)之后,形成的子矩阵就单纯取决于第四条边的位置(黄色):
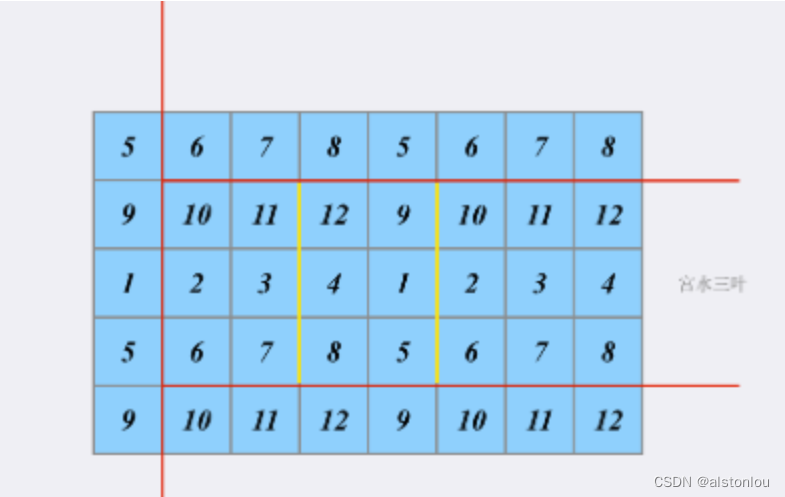
于是问题转换为[如何快速求得第四条边(黄色)的位置在哪]。
我们可以进一步将问题缩小,考虑矩阵之有一行(一维)的情况:
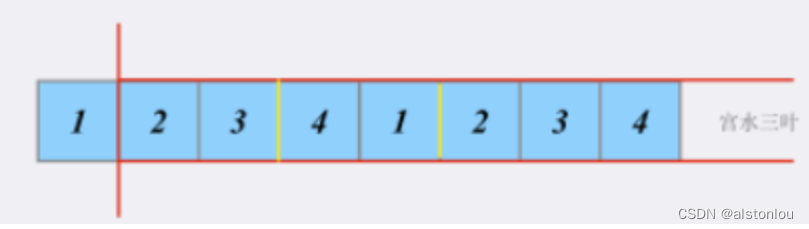
这时候问题进一步转换为[在一维数组中,求解和不超过K的最大连续子数组之和]。
对于这个一维问题,我们可以先预处理出[前缀和],然后枚举子数组的左端点,然后通过[二分]来求解其右端点的位置。
假定我们已经求得一维数组的前缀和数组sum,即可得下标范围[i,j]的和为:
areaSum(i,j) = sum[j] - sum[i-1] <=k
经过变形后得:
sum[j] <= k + sum[i-1]
我们两种思路来最大化areaSum(i,j):
- 确定(枚举)左端点位置
i,求得符合条件的最大右端点sum[j] - 确定(枚举)右端点位置
j,求得符合条件的最小左端点sum[i]
对于没有负权值的一维数组,我们可以枚举左端点i,同时利用前缀和的[单调递增]特性,通过[二分]找到符合sum[j] <= k +sum[i-1]条件的最大值sum[j],从而求解出答案
但是如果是含有负权值的话,前缀和将会丢失[单调递增]的特性,我们也就无法使用枚举i并结合[二分]查找j的做法。
这时候需要将过程反过来处理:我们从左到右枚举j,并使用[有序集合]结构维护遍历过的位置,找到符合sun[j] - k <= sum[i] 条件最小值sum[i],从而求解出答案。
基于上述分析,解决这样的一维数组问题复杂度是 O ( n l o g n ) O(n log n) O(nlogn)。将这样子思路应用到二维需要一点点抽象能力。
同时,将一维思路引用到本题(二维),复杂度要么是 O ( m 2 ∗ n l o g n ) O(m ^2 * n logn) O(m2∗nlogn)要么是 O ( n 2 ∗ m l o g m ) O(n^2 * m log m) O(n2∗mlogm)
我们先不考虑[最大化二分收益]问题,先假设我们是固定枚举[上下行]和[右边列],这时候唯一能够确定一个子矩阵则是取决于[左边列]:
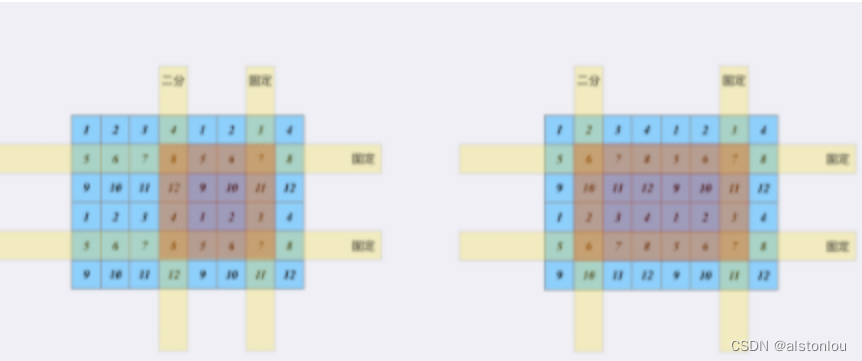
重点是如何与[一维]问题进行关联:显然[目标子矩阵的和]等于[子矩阵的右边列 与 原矩阵的左边列 形成的子矩阵和] - [子矩阵左边列 与 原矩阵左边列 形成的子矩阵和]
我们可以使用area[r]代表[子矩阵的右边列 与 原矩阵的左边列 形成的子矩阵之和],使用area[l-1]代表[子矩阵的左边列 与 原矩阵的左边列 形成的子矩阵和]的话,则有:
target = area[r] - area[l-1] <=k
这与我们[一维问题]完全一直,同时由[上下行]&[右边列]可与直接确定area[r]的大小,通过[有序集合]存储我们遍历r过程中固定所有area[r]从而实现[二分]查找符合area[r] - k <= area[l-1]条件的最小的area[l-1]。
至此,我们通过预处理前缀和+容斥原理彻底将题目转换为[一维问题]进行来求解。
其他解法
首先有三个变量row,col,res第一个记录行,第二个记录列,第三个记录矩形和
然后看二维矩阵matrix,我们有两个索引left,right,这两个索引代表列与列之间的范围。
开始先从第0列开始,同时也作为左边的列left,然后再取右边的列right逐渐将右移。并且记录同一行左边的列与右边的列的和.
这里有个需要注意的,我们首先是取第0列作为左边的列,然后右边的列依次从第0列开始逐渐到最后一列,在此期间同一行的左右列会逐渐相加。当我们这次一整个循环完,左边的列会更新成1,也就是for left in range(col),然后重置新一轮的计算和,再继续循环右边的列。
接下来当我们累加和计算完之后就相当于将二维变成了一维,之后我们将在这个一维里面计算最大的矩形和。一个列表lst用来存放累加的和,一个变量cur用来累加之前算出来的累加列表sums。
我们这里需要找到的是最大的矩形和,但是有一个条件,那就是不大于k。比如我们要求sums(i,j)=sums(0,j)-sums(0,i-1)那么我们可以把sums(i,j)=k且不大于k,sums(0,j)-sums(0,i-1)<=k,可以写成sums(0,j)-k<=sums(0,i-1),我们可以看这个式子是否成立。
所以当我们累加和第一个值之后loc = bisect.bisect_left(lst,cur-k)可以看成sums(0,j)-k<=sums(0,i-1),接下来进行一个if判断,如果成立那么cur-lst[loc]可以看成sums(0,j)-sums(0,i-1)<=k计算出值,之后进行res最大值计算。
想不起来可以参看
https://leetcode-cn.com/problems/max-sum-of-rectangle-no-larger-than-k/solution/javacong-bao-li-kai-shi-you-hua-pei-tu-pei-zhu-shi/
代码
class Solution:def maxSumSubmatrix(self, matrix: List[List[int]], k: int) -> int:import bisectrow = len(matrix)col = len(matrix[0])res = float("-inf")for left in range(col):# 以left为左边界,每行的总和_sum = [0] * rowfor right in range(left, col):for j in range(row):_sum[j] += matrix[j][right]# 在left,right为边界下的矩阵,求不超过K的最大数值和arr = [0]cur = 0for tmp in _sum:cur += tmp# 二分法loc = bisect.bisect_left(arr, cur - k)if loc < len(arr):res = max(cur - arr[loc], res)# 把累加和加入bisect.insort(arr, cur)return res复杂度分析
时间复杂度: O ( m 2 ∗ n 2 ) O(m^2 * n^2 ) O(m2∗n2)
空间复杂度: O ( n ) O(n) O(n)
相关文章:

算法第十二天-矩形区域不超过K的最大数值和
矩形区域不超过K的最大数值和 题目要求 解题思路 来自[宫水三叶] 从题面来看显然是一道[二维前缀和]的题目。本题预处理前缀和的复杂度为O(m* n) 搜索所有子矩阵需要枚举[矩形左上角]和[矩形右下角],复杂度是 O ( m 2 ∗ n 2 ) O(m^2 * n^2) O(m2∗n2),…...

【js】js数组对象去重:
文章目录 一、Map()二、对象访问属性的方法三、indexOf()四、双层for循环 let arrObj [{ name: "小红", id: 1 },{ name: "小橙", id: 1 },{ name: "小黄", id: 4 },{ name: "小绿", id: 3 },{ name: "小青", id: 1 },{ na…...
python高校舆情分析系统+可视化+情感分析 舆情分析+Flask框架(源码+文档)✅
毕业设计:2023-2024年计算机专业毕业设计选题汇总(建议收藏) 毕业设计:2023-2024年最新最全计算机专业毕设选题推荐汇总 🍅感兴趣的可以先收藏起来,点赞、关注不迷路,大家在毕设选题ÿ…...

Phaser详解
Phaser是一个相对较新且功能强大的同步原语,它于Java 7中引入,用于协调并行任务的执行。与CyclicBarrier和CountDownLatch等传统的同步工具相比,Phaser提供了更灵活和更高级的功能,特别是在处理动态和可变的并行任务集合时。 1.P…...

2个nodejs进程利用redis 实现订阅发布
1.新建文件 redis_db.js use strict;const redis require(redis); const options {host: "127.0.0.1",port: 6379,password: "123456", // CONFIG SET requirepass "123456" }var array [] for(var i0; i<3; i){const client redis.crea…...

LeetCode——2397. 被列覆盖的最多行数
通过万岁!!! 题目:给你一个二维数组,然后里面是0和1,然后让你从里面选择numSelect列,使得去掉选择的列以后不存在1的行的数量最少。思路: 看到这个题目,本来以为是每一列…...

java通过HttpClient方式实现https请求的工具类(绕过证书验证)
目录 一、引入依赖包二、HttpClient方式实现的https请求工具类三、测试类 一、引入依赖包 引入相关依赖包 <!--lombok用于简化实体类开发--><dependency><groupId>org.projectlombok</groupId><artifactId>lombok</artifactId><option…...

【自学笔记】01Java基础-07面向对象基础-04接口与内部类详解
记录学习Java基础中有关接口类和内部类的知识。 1 接口 interface 关键字用于定义接口类,接口类是一系列方法的声明,一般只有方法的特征没有方法的实现,因此可以被不同的类接入实现,而这些实现可以具有不同的行为(功…...

【cmu15445c++入门】(5)c++中的模板类
一、template模板类 除了模板方法【cmu15445c入门】(4)c中的模板方法 模板也可以用来实现类 二、代码 /*** file templated_classes.cpp* author Abigale Kim (abigalek)* brief Tutorial code for templated classes.*/// Includes std::cout (printing). #include <io…...

MongoDB聚合:$bucket
$bucket将输入文档按照指定的表达式和边界进行分组,每个分组为一个文档,称为“桶”,每个桶都有一个唯一的_id,其值为文件桶的下线。每个桶中至少要包含一个输入文档,也就是没有空桶。 使用 语法 {$bucket: {groupBy…...

从优化设计到智能制造:生成式AI在可持续性3D打印中的潜力和应用
可持续性是现代工业中一个紧迫的问题,包括 3D 打印领域。为了满足环保制造实践日益增长的需求,3D 打印已成为一种有前景的解决方案。然而,要使 3D 打印更具可持续性,还存在一些需要解决的挑战。生成式人工智能作为一股强大的力量&…...
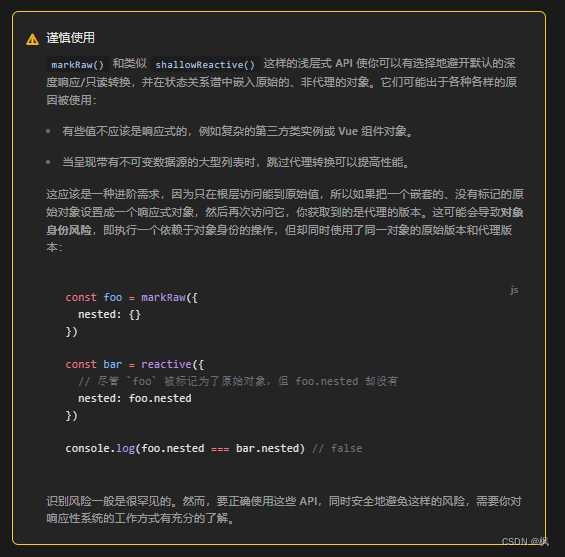
vue3 响应式api中特殊的api
系列文章目录 TypeScript 从入门到进阶专栏 文章目录 系列文章目录一、shallowRef()二、triggerRef()三、customRef()四、shallowReactive()五、shallowReadonly()六、toRaw()七、markRaw()八、effectScope()九、getCurrentScope() 一、shallowRef() shallowRef()是一个新的响…...

【大厂算法面试冲刺班】day2:合并两个有序链表
将两个升序链表合并为一个新的 升序 链表并返回。新链表是通过拼接给定的两个链表的所有节点组成的。 递归 class Solution {public ListNode mergeTwoLists(ListNode l1, ListNode l2) {if (l1 null) {return l2;}else if (l2 null) {return l1;}else if (l1.val < l2.…...
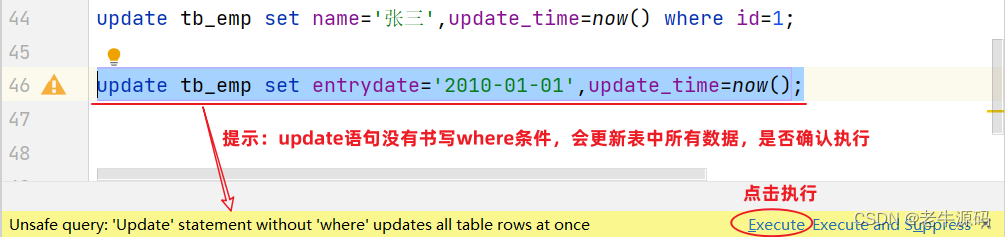
【JaveWeb教程】(19) MySQL数据库开发之 MySQL数据库操作-DML 详细代码示例讲解
目录 3. 数据库操作-DML3.1 增加(insert)3.2 修改(update)3.3 删除(delete)3.4 总结 3. 数据库操作-DML DML英文全称是Data Manipulation Language(数据操作语言),用来对数据库中表的数据记录进行增、删、改操作。 添加数据(INSERT)修改数据…...

Web前端篇——ElementUI之el-scrollbar + el-backtop + el-timeline实现时间轴触底刷新和一键返回页面顶部
ElementUI之el-scrollbar el-backtop el-timeline实现时间轴触底刷新和一键返回页面顶部。 背景:ElementUI的版本(vue.global.js 3.2.36, index.css 2.4.4, index.full.js 2.4.4) 废话不多说,先看动…...

CAS-ABA问题编码实战
多线程情况下演示AtomicStampedReference解决ABA问题 package com.nanjing.gulimall.zhouyimo.test;import java.util.concurrent.TimeUnit; import java.util.concurrent.atomic.AtomicInteger; import java.util.concurrent.atomic.AtomicStampedReference;/*** @author zho…...

Linux 常用进阶指令
我是南城余!阿里云开发者平台专家博士证书获得者! 欢迎关注我的博客!一同成长! 一名从事运维开发的worker,记录分享学习。 专注于AI,运维开发,windows Linux 系统领域的分享! 其他…...
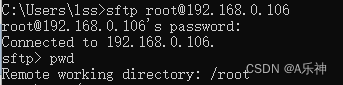
windows通过ssh连接Liunx服务器并实现上传下载文件
连接ssh 输入:ssh空格用户名ip地址,然后按Enter 有可能出现下图提示,输入yes 回车即可 输入 password ,注意密码是不显示的,输入完,再按回车就行了 以上是端口默认22情况下ssh连接,有些公司它…...

【K8S 存储卷】K8S的存储卷+PV/PVC
目录 一、K8S的存储卷 1、概念: 2、挂载的方式: 2.1、emptyDir: 2.2、hostPath: 2.3、NFS共享存储: 二、PV和PVC: 1、概念 2、请求方式 3、静态请求流程图: 4、PV和PVC的生命周期 5、…...

工业智能网关如何保障数据通信安全
工业智能网关是组成工业物联网的重要设备,不仅可以起到数据交换、通信、边缘计算的功能,还可以发挥数据安全保障功能,保障工业物联网稳定、可持续。本篇就为大家简单介绍一下工业智能网关增强和确保数据通信安全的几种措施: 1、软…...

深度学习在微纳光子学中的应用
深度学习在微纳光子学中的主要应用方向 深度学习与微纳光子学的结合主要集中在以下几个方向: 逆向设计 通过神经网络快速预测微纳结构的光学响应,替代传统耗时的数值模拟方法。例如设计超表面、光子晶体等结构。 特征提取与优化 从复杂的光学数据中自…...

k8s从入门到放弃之Ingress七层负载
k8s从入门到放弃之Ingress七层负载 在Kubernetes(简称K8s)中,Ingress是一个API对象,它允许你定义如何从集群外部访问集群内部的服务。Ingress可以提供负载均衡、SSL终结和基于名称的虚拟主机等功能。通过Ingress,你可…...

2025年能源电力系统与流体力学国际会议 (EPSFD 2025)
2025年能源电力系统与流体力学国际会议(EPSFD 2025)将于本年度在美丽的杭州盛大召开。作为全球能源、电力系统以及流体力学领域的顶级盛会,EPSFD 2025旨在为来自世界各地的科学家、工程师和研究人员提供一个展示最新研究成果、分享实践经验及…...

MongoDB学习和应用(高效的非关系型数据库)
一丶 MongoDB简介 对于社交类软件的功能,我们需要对它的功能特点进行分析: 数据量会随着用户数增大而增大读多写少价值较低非好友看不到其动态信息地理位置的查询… 针对以上特点进行分析各大存储工具: mysql:关系型数据库&am…...

连锁超市冷库节能解决方案:如何实现超市降本增效
在连锁超市冷库运营中,高能耗、设备损耗快、人工管理低效等问题长期困扰企业。御控冷库节能解决方案通过智能控制化霜、按需化霜、实时监控、故障诊断、自动预警、远程控制开关六大核心技术,实现年省电费15%-60%,且不改动原有装备、安装快捷、…...
指令的指南)
在Ubuntu中设置开机自动运行(sudo)指令的指南
在Ubuntu系统中,有时需要在系统启动时自动执行某些命令,特别是需要 sudo权限的指令。为了实现这一功能,可以使用多种方法,包括编写Systemd服务、配置 rc.local文件或使用 cron任务计划。本文将详细介绍这些方法,并提供…...

CocosCreator 之 JavaScript/TypeScript和Java的相互交互
引擎版本: 3.8.1 语言: JavaScript/TypeScript、C、Java 环境:Window 参考:Java原生反射机制 您好,我是鹤九日! 回顾 在上篇文章中:CocosCreator Android项目接入UnityAds 广告SDK。 我们简单讲…...

【AI学习】三、AI算法中的向量
在人工智能(AI)算法中,向量(Vector)是一种将现实世界中的数据(如图像、文本、音频等)转化为计算机可处理的数值型特征表示的工具。它是连接人类认知(如语义、视觉特征)与…...

华硕a豆14 Air香氛版,美学与科技的馨香融合
在快节奏的现代生活中,我们渴望一个能激发创想、愉悦感官的工作与生活伙伴,它不仅是冰冷的科技工具,更能触动我们内心深处的细腻情感。正是在这样的期许下,华硕a豆14 Air香氛版翩然而至,它以一种前所未有的方式&#x…...

Aspose.PDF 限制绕过方案:Java 字节码技术实战分享(仅供学习)
Aspose.PDF 限制绕过方案:Java 字节码技术实战分享(仅供学习) 一、Aspose.PDF 简介二、说明(⚠️仅供学习与研究使用)三、技术流程总览四、准备工作1. 下载 Jar 包2. Maven 项目依赖配置 五、字节码修改实现代码&#…...
