【C++】位图
文章目录
- 位图概念
- 位图操作
- 位图代码
- 位图应用
位图概念
boss直接登场:
给40亿个不重复的无符号整数,没排过序。给一个无符号整数,如何快速判断一个数是否在这40亿个数中❓
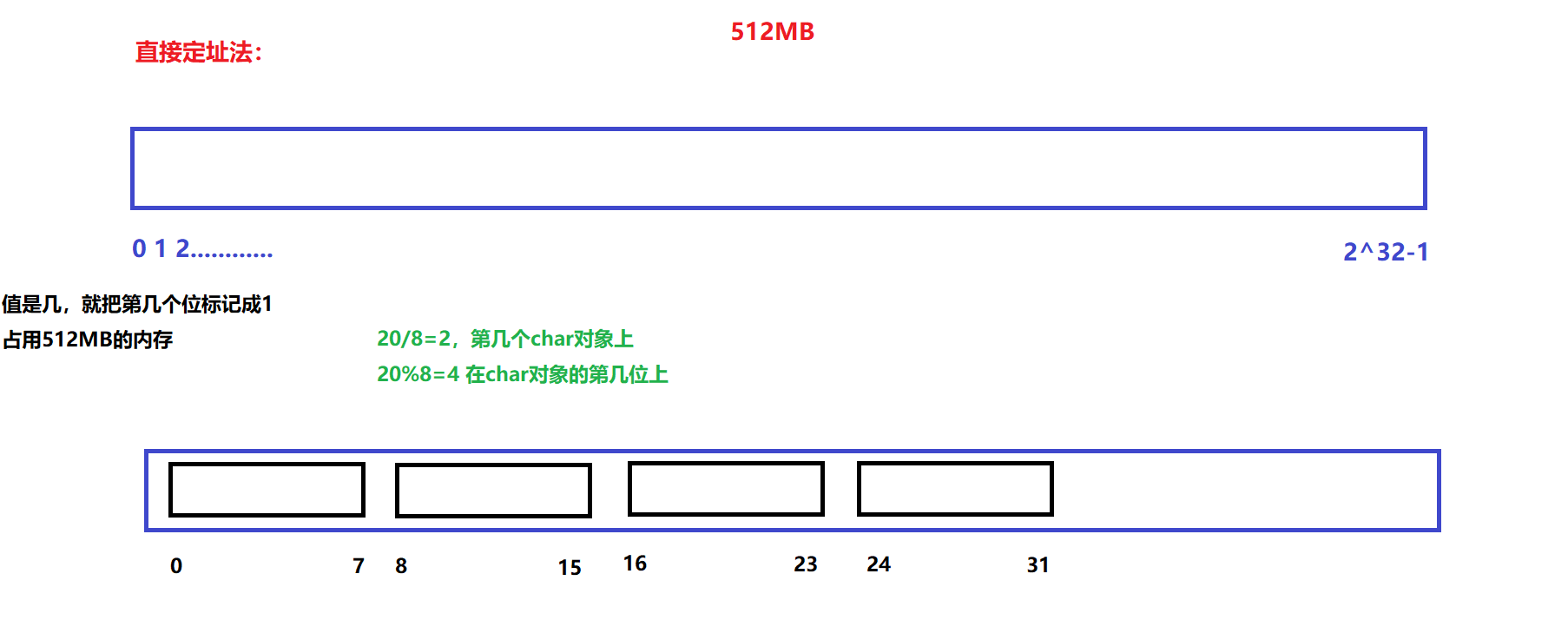
40亿个整数,大概就是16GB。40亿个字节大概就是4GB。
1Byte=8bit
1KB=1024Byte
1MB=1024KB=1024*1024=1048576字节
1GB=1024MB=1024*1048576≈10亿字节,所以4GB约等于40亿字节
1TB=1024GB
如果采用排序+二分的做法来查找:排序要用到数组,要开出16GB大的数组,排在数组里才能进行二分查找,但是这些数组在内存里放不下,所以排序都排不了。那只能放到磁盘上,那数据在磁盘上就不能用二分了,不支持下标,效率也慢。
如果用红黑树和哈希表:数组都存放不下,红黑树和哈希表更不用说了,红黑树三叉链结构+颜色,消耗更大,哈希表也有消耗:存放_next指针,负载因子等问题,内存放不下。
下面,我们解决这个问题的方法是位图
这个问题是在不在的问题,是key的模型,那我们可以标记在还是不在,我们只需要一个比特位就可以标记在还是不在
数据是否在给定的整形数据中,结果是在或者不在,刚好是两种状态,那么可以使用一个二进制比特位来代表数据是否存在的信息,如果二进制比特位为1,代表存在,为0代表不存在。
位图概念
所谓位图,就是用每一位来存放某种状态,适用于海量数据,数据无重复的场景。通常是用来判断某个数据存不存在的
位图操作
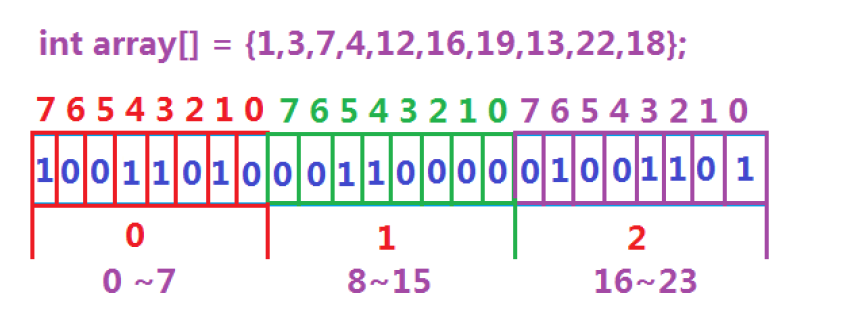
位图核心的三个操作是set、reset和test。
set是将x对应的比特位置设为1,reset是将x对应的比特位置设为0,test用来查看x在不在
set将对应的比特位置设为1:_bits[i]|=(1<<j)
reset将对应的比特位置设为0:_bits[i]&=(~(1<<j))
test查看x在或不在:_bits[i]&(1<<j)
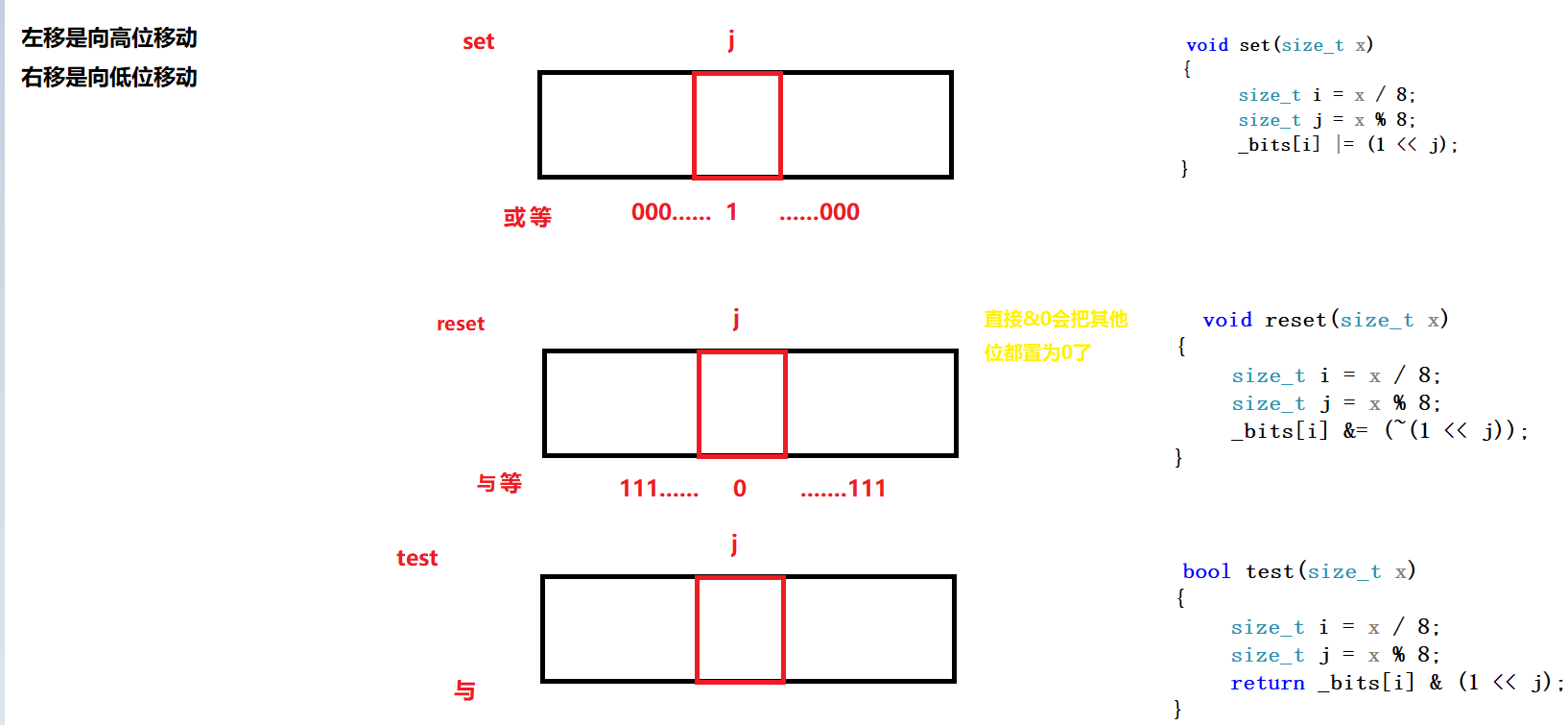
void set(size_t x){size_t i = x / 8;size_t j = x % 8;_bits[i] |= (1 << j);}void reset(size_t x){size_t i = x / 8;size_t j = x % 8;_bits[i] &= (~(1 << j));}bool test(size_t x){size_t i = x / 8;size_t j = x % 8;return _bits[i] & (1 << j);}
位图代码
#pragma once
#include <iostream>
#include <vector>
using namespace std;namespace hwc
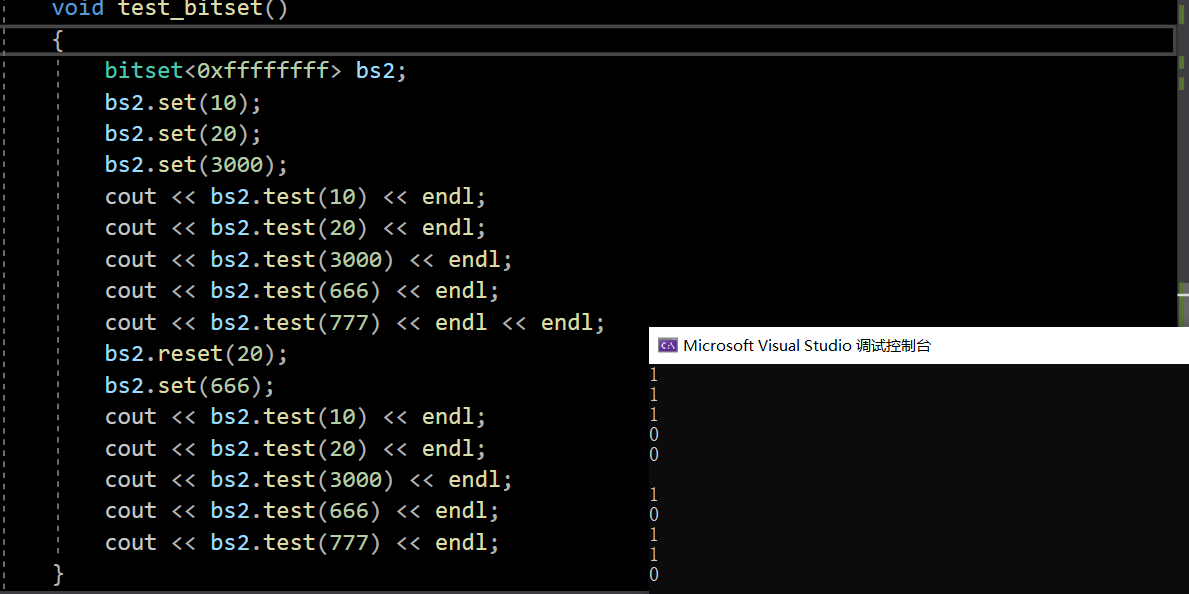
{template<size_t N>class bitset{public:bitset(){_bits.resize(N/8+1, 0);}void set(size_t x){size_t i = x / 8;size_t j = x % 8;_bits[i] |= (1 << j);}void reset(size_t x){size_t i = x / 8;size_t j = x % 8;_bits[i] &= (~(1 << j));}bool test(size_t x){size_t i = x / 8;size_t j = x % 8;return _bits[i] & (1 << j);}private:vector<char> _bits;};void test_bitset(){//bitset<100> bs1;//bitset<-1> bs2;//bitset<0xffffffff> bs2;bs2.set(10);bs2.set(20);bs2.set(3000);cout << bs2.test(10) << endl;cout << bs2.test(20) << endl;cout << bs2.test(3000) << endl;cout << bs2.test(666) << endl;cout << bs2.test(777) << endl << endl;bs2.reset(20);bs2.set(666);cout << bs2.test(10) << endl;cout << bs2.test(20) << endl;cout << bs2.test(3000) << endl;cout << bs2.test(666) << endl;cout << bs2.test(777) << endl;}
}
小细节:(-1)的size_t类型
实际上,库里面也有位图:
位图应用
\1. 快速查找某个数据是否在一个集合中
\2. 排序
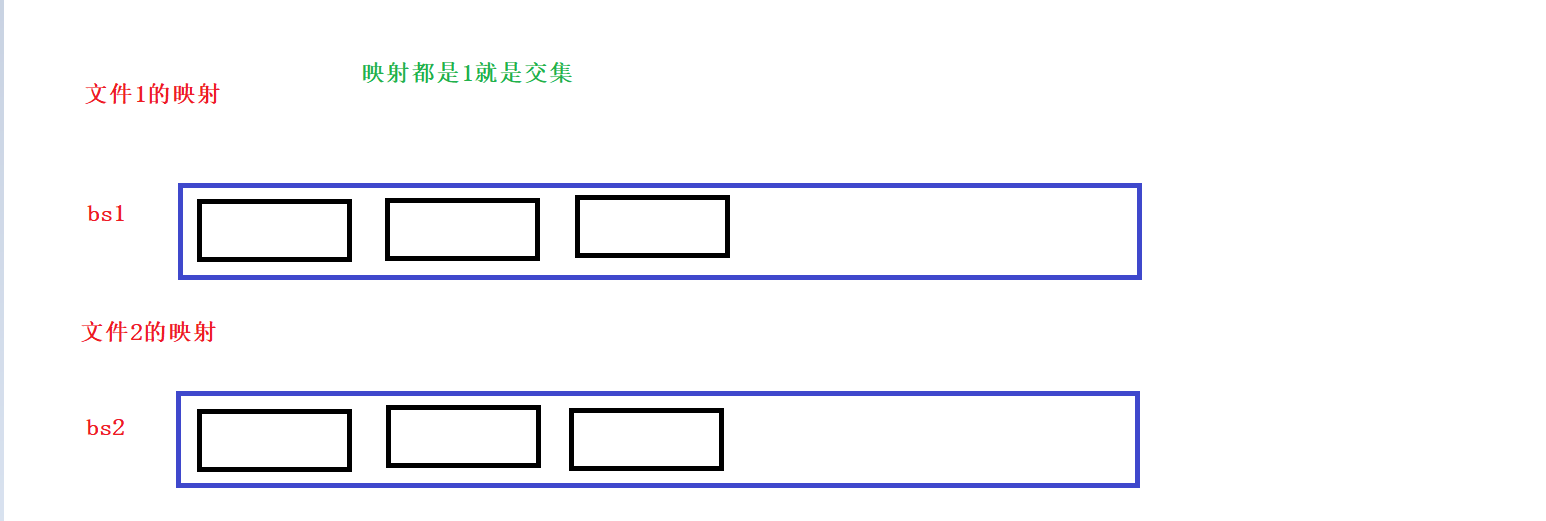
\3. 求两个集合的交集、并集等
\4. 操作系统中磁盘块标记
给定 100 亿个整数,设计算法找到只出现一次的整数
100亿个数字找到只出现一次的整数,这是KV模型的统计次数,数字有三种状态:0次、1次、1次以上,。这三种状态需要用两个比特位就可以表示,分别位00代表0次,01代表1次,10代表1次以上既可以。我们可以采用两个位图来实现,复用上面所实现的位图即可解决问题
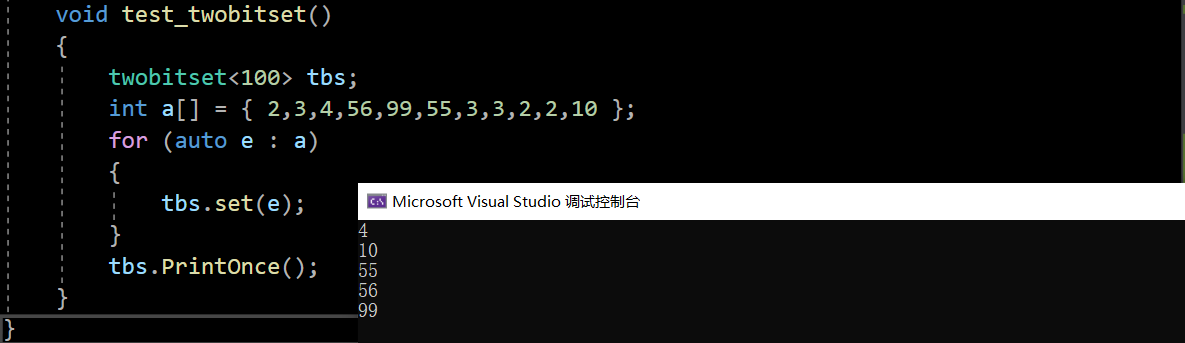
template<size_t N>class twobitset{public:void set(size_t x){if (!_bs1.test(x) && !_bs2.test(x))//00{_bs2.set(x);//01}else if (!_bs1.test(x) && _bs2.test(x))//01{_bs1.set(x);_bs2.reset(x);//10}//10不变}void PrintOnce(){for (size_t i = 0; i < N; ++i){if (!_bs1.test(i) && _bs2.test(i)){cout << i << endl;}}cout << endl;}private:bitset<N> _bs1;bitset<N> _bs2;};void test_twobitset(){twobitset<100> tbs;int a[] = { 2,3,4,56,99,55,3,3,2,2,10 };for (auto e : a){tbs.set(e);}tbs.PrintOnce();}
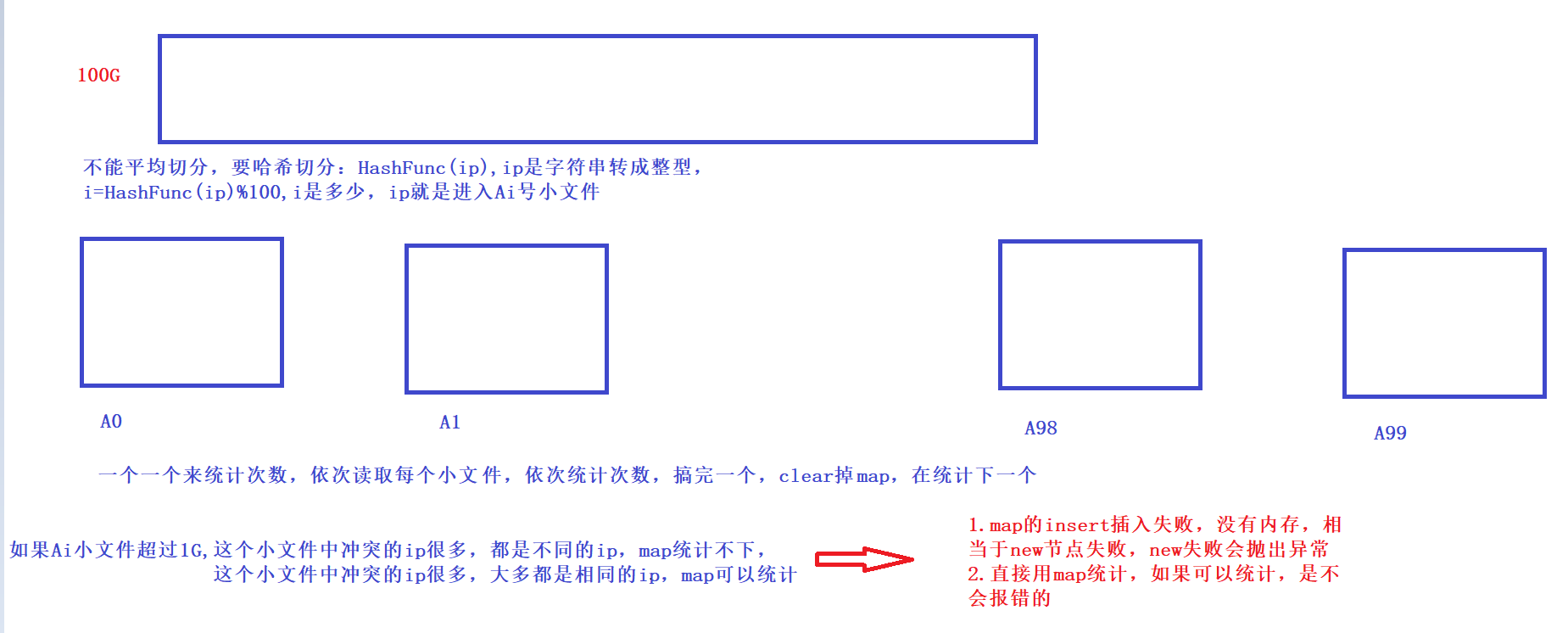
给两个文件,分别有100亿个整数,我们只有1G内存,如何找到两个文件交集?
1 个文件有 100 亿个 int,1G内存,设计算法找到出现次数不超过2次的所有整数
这与上面的类似,多判断一次
把10->11,最后找不超过两次的整数
给一个超过100G大小的log file,log中存着IP地址,设计算法找到出现次数最多的IP地址
统计次数自然是要map的,map有附带消耗,三叉链。位图只能判断在不在。所以还是要用map统计的:
我们可以把整个文件通过哈希切分成小的文件,然后去进行统计次数,但是如果小的文件超过1G,说明了这个小文件有两种情况:
1.这个小文件冲突的ip很多,但都是不同的ip,map统计不下------->map的insert插入失败,没有内存,相当于new节点失败,new失败会抛出异常
2.这个肖文杰冲突的ip很多,大多都是相同的ip,map可以统计-------->直接用map统计,可以统计,不会报错
位图特点:位图只能处理整形。采用位图标记字符串时,必须先将字符串转化为整形的数字,找到位图对应的比特位置
相关文章:
【C++】位图
文章目录位图概念位图操作位图代码位图应用位图概念 boss直接登场: 给40亿个不重复的无符号整数,没排过序。给一个无符号整数,如何快速判断一个数是否在这40亿个数中❓ 40亿个整数,大概就是16GB。40亿个字节大概就是4GB。 1Byt…...

蓝桥杯-考勤刷卡
蓝桥杯-考勤刷卡1、问题描述2、解题思路3、代码实现1、问题描述 小蓝负责一个公司的考勤系统, 他每天都需要根据员工刷卡的情况来确定 每个员工是否到岗。 当员工刷卡时, 会在后台留下一条记录, 包括刷卡的时间和员工编号, 只 要在一天中员工刷过一次卡, 就认为他到岗了。 现在…...

如何利用站内推广和站外推广提高转化率?
在如今的网络时代,拥有一个好的网站是非常重要的。但是,光有一个好的网站是不够的,为了达到我们的目标,需要不断地提高网站的转化率。而在实现这个目标的过程中,站内推广和站外推广是两个非常关键的因素。 站内推广是…...
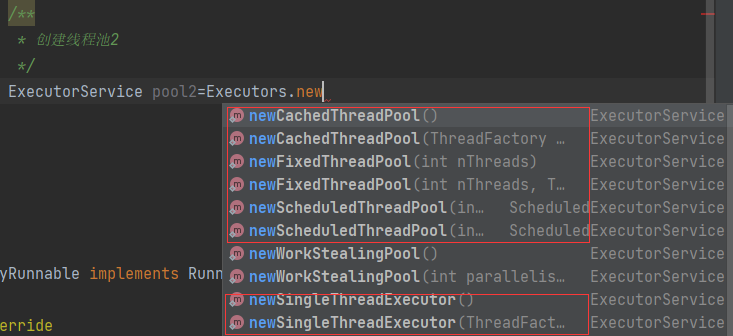
Java多线程(三)——线程池及定时器
线程池就是一个可以复用线程的技术。前面三种多线程方法就是在用户发起一个线程请求就创建一个新线程来处理,下次新任务来了又要创建新线程,而创建新线程的开销是很大的,这样会严重影响系统的性能。线程池就相当于预先创建好几个线程…...

Linux命令行安装Oracle19c教程和踩坑经验
安装 下载 从 Oracle官方下载地址 需要的版本,本次安装是在Linux上使用yum安装,因此下载的是RPM。另外,需要说明的是,Oracle加了锁的下载需要登录用户才能安装,而用户是可以免费注册的,这里不做过多说明。 …...

Linux常用命令等
目录 1.Linux常用命令 (1)系统命令 (2)文件操作命令 2.vim编辑器 3.linux系统中,软件安装 (1) rpm 安装,RedHat Package Manager (2)yum 安装 (3)源代码编译安装 1.Linux常用命令 Linux命令是非常多的,对于像嵌入式开发工程师,运维工程师需要掌握的命令是非常多的.对于…...

CEC2014:鱼鹰优化算法(Osprey optimization algorithm,OOA)求解CEC2014(提供MATLAB代码
一、鱼鹰优化算法简介 鱼鹰优化算法(Osprey optimization algorithm,OOA)由Mohammad Dehghani 和 Pavel Trojovsk于2023年提出,其模拟鱼鹰的捕食行为。 鱼鹰是鹰形目、鹗科、鹗属的仅有的一种中型猛禽。雌雄相似。体长51-64厘米…...
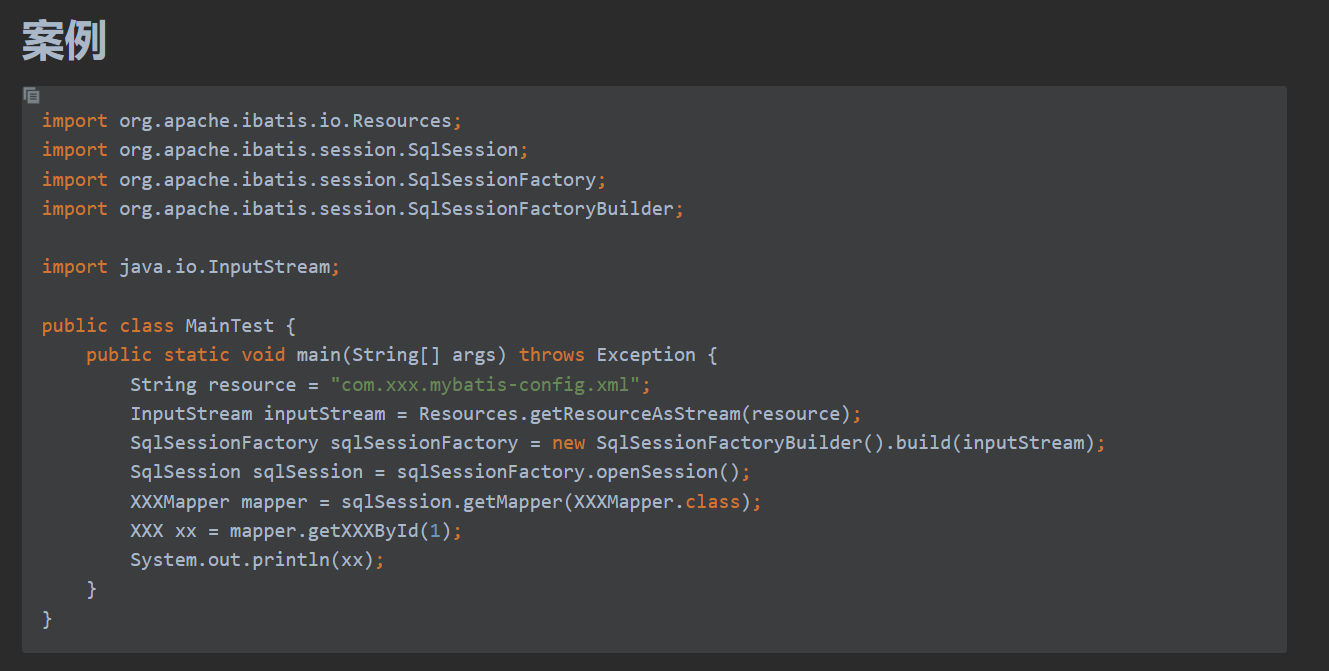
MyBatis底层原理【源码运行时序图】
MyBatis初始化流程🛷 以下代码为例🎉 🎇可对应源码阅读 MyBatis初始化流程✨ #mermaid-svg-yoG1e8Dnp3UIAOUW {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-yoG1e8Dnp3UIAOU…...

k8s 系列之 CoreDNS 解读
k8s 系列之 CoreDNS CoreDNS工作原理 kuberntes 中的 pod 基于 service 域名解析后,再负载均衡分发到 service 后端的各个 pod 服务中,如果没有 DNS 解析,则无法查到各个服务对应的 service 服务 在 Kubernetes 中,服务发现有几…...

从测试鸡蛋硬度到跳表的设计
我回忆起六七年前的一道题鸡蛋掉落问题,有幸在leetCode上找到题目了 原题是2枚鸡蛋 leetCode有拓展,k枚鸡蛋 具体的思路是这样的。 以2枚鸡蛋验证100层为例 不能直接二分查找,因为你在50层测试时,如果直接鸡蛋碎了,那…...
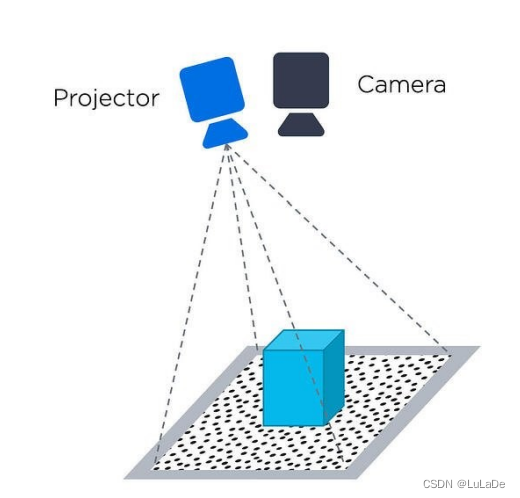
3D立体视觉成像原理介绍【一 】
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录前言什么是基线?基线是如何影响3D图像质量激光三角测量飞行时间结构光相机时间编码结构光前言 本文将介绍3D立体视觉的成像原理,包括【激光三…...

CEC2021:鱼鹰优化算法(Osprey optimization algorithm,OOA)求解CEC2021(提供MATLAB代码
一、鱼鹰优化算法简介 鱼鹰优化算法(Osprey optimization algorithm,OOA)由Mohammad Dehghani 和 Pavel Trojovsk于2023年提出,其模拟鱼鹰的捕食行为。 鱼鹰是鹰形目、鹗科、鹗属的仅有的一种中型猛禽。雌雄相似。体长51-64厘米…...

0301_对应的南京比特物联网
0301_对应的南京比特物联网目录概述需求:设计思路实现思路分析1.流程拓展实现性能参数测试:参考资料和推荐阅读Survive by day and develop by night. talk for import biz , show your perfect code,full busy,skip hardness,make a better …...

钡铼技术BL302 ARM工控机QT图形化界面开发的实践
QT是一种跨平台的应用程序框架,用于开发图形用户界面(GUI)、网络应用程序和嵌入式应用程序。QT提供了丰富的GUI组件和工具,使开发人员能够轻松地创建专业级别的应用程序。QT使用C编写,支持多种操作系统,包括Windows、Linux、macOS…...
)
Python try except异常处理详解(入门必读)
Python 中,用try except语句块捕获并处理异常,其基本语法结构如下所示: try:可能产生异常的代码块 except [ (Error1, Error2, ... ) [as e] ]:处理异常的代码块1 except [ (Error3, Error4, ... ) [as e] ]:处理异常的代码块2 except [Exc…...

信息系统基本知识(三)软件工程
1.4 软件工程 定义:将系统的、规范的、可度量的工程化方法应用于软件开发、运行和维护的全过程即上述方法的研究 软件工程由方法、工具和过程三个部分组成 1.4.1 需求分析 软件需求是指用户对新系统在功能、行为、性能、设计约束等方面的期望。 需求层次 业务…...

Linux下软件部署安装管理----rpmbuild打包rpm包部署安装
来源:微信公众号「编程学习基地」 文章目录1.安装rpmbuild2.rpm包制作打包rpm包3.rpm包安装4.rpm包卸载1.安装rpmbuild yum install rpmbuild yum install rpmdevtools创建rpm包管理路径,生成rpm相关目录 RPM打包的时候需要编译源码,还需要…...
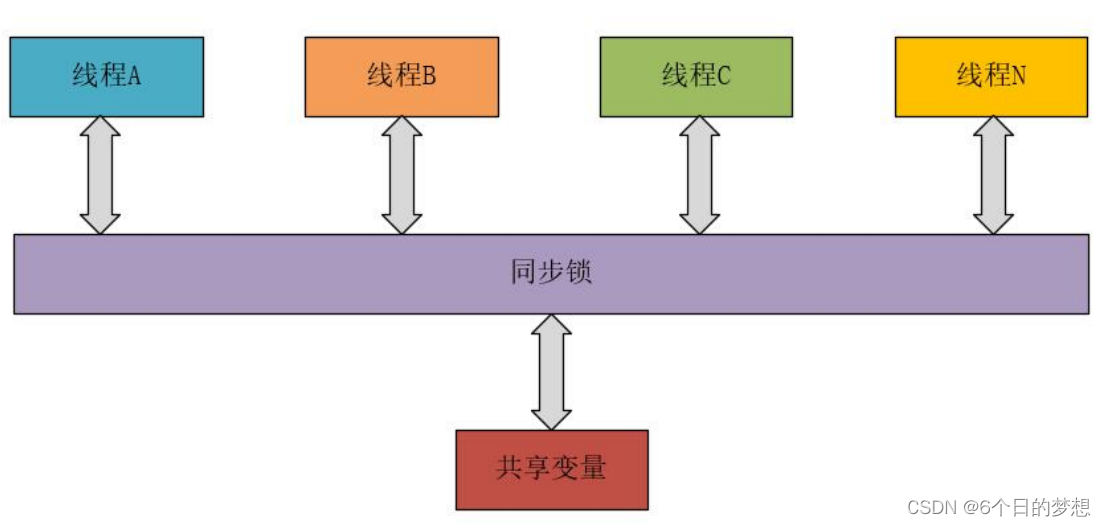
ThreadLocal学会了这些,你也能和面试官扯皮了!
前言 我们都知道,在多线程环境下访问同一个共享变量,可能会出现线程安全的问题,为了保证线程安全,我们往往会在访问这个共享 变量的时候加锁,以达到同步的效果,如下图所示。 对共享变量加锁虽然能够保证线程的安全,但是却增加了开发人员对锁的使用技能,如果锁使用不当…...

【存储】存储特性
存储特性精简配置技术(SmartThin)SmartThin主要功能容量虚拟化存储空间写时分配:Capacity-on-Write读写重定向:Direct-on-Time应用场景及配置流程存储分层技术(SmartTier)存储分层工作原理关键技术容量初始…...
Qt使用OpenGL进行多线程离屏渲染
基于Qt Widgets的Qt程序,控件的刷新默认状况下都是在UI线程中依次进行的,换言之,各个控件的QWidget::paintEvent方法会在UI线程中串行地被调用。若是某个控件的paintEvent很是耗时(等待数据时间CPU处理时间GPU渲染时间)…...
)
React Native 开发环境搭建(全平台详解)
React Native 开发环境搭建(全平台详解) 在开始使用 React Native 开发移动应用之前,正确设置开发环境是至关重要的一步。本文将为你提供一份全面的指南,涵盖 macOS 和 Windows 平台的配置步骤,如何在 Android 和 iOS…...

黑马Mybatis
Mybatis 表现层:页面展示 业务层:逻辑处理 持久层:持久数据化保存 在这里插入图片描述 Mybatis快速入门 
visual studio 2022更改主题为深色
visual studio 2022更改主题为深色 点击visual studio 上方的 工具-> 选项 在选项窗口中,选择 环境 -> 常规 ,将其中的颜色主题改成深色 点击确定,更改完成...

spring:实例工厂方法获取bean
spring处理使用静态工厂方法获取bean实例,也可以通过实例工厂方法获取bean实例。 实例工厂方法步骤如下: 定义实例工厂类(Java代码),定义实例工厂(xml),定义调用实例工厂ÿ…...

零基础设计模式——行为型模式 - 责任链模式
第四部分:行为型模式 - 责任链模式 (Chain of Responsibility Pattern) 欢迎来到行为型模式的学习!行为型模式关注对象之间的职责分配、算法封装和对象间的交互。我们将学习的第一个行为型模式是责任链模式。 核心思想:使多个对象都有机会处…...

网站指纹识别
网站指纹识别 网站的最基本组成:服务器(操作系统)、中间件(web容器)、脚本语言、数据厍 为什么要了解这些?举个例子:发现了一个文件读取漏洞,我们需要读/etc/passwd,如…...
与常用工具深度洞察App瓶颈)
iOS性能调优实战:借助克魔(KeyMob)与常用工具深度洞察App瓶颈
在日常iOS开发过程中,性能问题往往是最令人头疼的一类Bug。尤其是在App上线前的压测阶段或是处理用户反馈的高发期,开发者往往需要面对卡顿、崩溃、能耗异常、日志混乱等一系列问题。这些问题表面上看似偶发,但背后往往隐藏着系统资源调度不当…...

【VLNs篇】07:NavRL—在动态环境中学习安全飞行
项目内容论文标题NavRL: 在动态环境中学习安全飞行 (NavRL: Learning Safe Flight in Dynamic Environments)核心问题解决无人机在包含静态和动态障碍物的复杂环境中进行安全、高效自主导航的挑战,克服传统方法和现有强化学习方法的局限性。核心算法基于近端策略优化…...

基于Java+MySQL实现(GUI)客户管理系统
客户资料管理系统的设计与实现 第一章 需求分析 1.1 需求总体介绍 本项目为了方便维护客户信息为了方便维护客户信息,对客户进行统一管理,可以把所有客户信息录入系统,进行维护和统计功能。可通过文件的方式保存相关录入数据,对…...

【网络安全】开源系统getshell漏洞挖掘
审计过程: 在入口文件admin/index.php中: 用户可以通过m,c,a等参数控制加载的文件和方法,在app/system/entrance.php中存在重点代码: 当M_TYPE system并且M_MODULE include时,会设置常量PATH_OWN_FILE为PATH_APP.M_T…...