Leetcode 494 目标和
题意理解:
给你一个非负整数数组
nums和一个整数target。向数组中的每个整数前添加
'+'或'-',然后串联起所有整数,可以构造一个 表达式 :
- 例如,
nums = [2, 1],可以在2之前添加'+',在1之前添加'-',然后串联起来得到表达式"+2-1"。返回可以通过上述方法构造的、运算结果等于
target的不同 表达式 的数目。
简单来说:就是在元素前面加‘+’或‘-’使其结果值为target。
可以将其思路转换为:将数组元素分为两部分,其差为target。
则有part1-part2=target,part1+part2=sum
part1=(sum+target)/2
固有我们需要将数组元素分为两部分,一部分较大的为part1=(sum+target)/2,较小的部分为part2=(sum-target)/2。
此时,我们再次转变思路:将其构造成0-1背包问题:
背包大小为m=(sum+target)/2
物品为[0,n]的元素,其价值和重量都是nums[]
接下来,使用动态规划中的0-1背包思路解决问题。
解题思路:
首先理解题意,将其转换为一个背包问题,使用动态规划的思路来求解。
动态规划五部曲:
(1)dp[i][j]或dp[i]的含义
(2)递推公式
(3)根据题意初始化
(4)遍历求解:先遍历包还是先遍历物品
(5)打印——debug
1.动态规划二维dp数组
- dp[i][j]表示[0,i]的元素装满大小为j的背包有多少种方法。
- 递推公式:dp[i][j]=dp[i-1][j]+dp[i-1][j-nums[i]],
- 当当前物品大于当前背包的大小时,放满大小为j的背包的方法数仍就为dp[i-1][j].
- 当当前物品小于等于当前背包的大小时,放满大小为j的背包的方法数=dp[i-1][j]+dp[i-1][j-nums[i]],其中dp[i-1][j-nums[i]]是增加了物品nums[i]后增加的方法数。
- 初始化:初始化第一列,其中特别的:放满背包大小0 有多少种方法——要么什么也不放,要么放入大小为0的物品。初始化时要根据问题,具体分析。
- 遍历:由于二维数组保留了两个维度所有值,所以先便利包还是先遍历物品都可以
public int findTargetSumWays(int[] nums, int target) {int sum=0;for(int num:nums){sum+=num;}//是否能按照需求分成两部分if((sum+target)%2!=0) return 0;if((sum-target)%2!=0) return 0;//把所有值当作整数,分成两部分一正一负即可,所以如果target总保持为正数if(target<0) target=-target;int size= (int)Math.ceil((float)(sum+target)/2);int dp[][]=new int[nums.length][size+1];//初始化for(int[] temp:dp) Arrays.fill(temp,0);int countZero=0;for(int i=0;i<nums.length;i++){if(nums[i]==0) countZero++;dp[i][0]=countZero+1;}for(int j=1;j<=size;j++){if(nums[0]==j) dp[0][j]=1;else dp[0][j]=0;}//遍历顺序for(int i=1;i< nums.length;i++){for(int j=0;j<=size;j++){if(j<nums[i]){dp[i][j]=dp[i-1][j];}else{dp[i][j]=dp[i-1][j]+dp[i-1][j - nums[i]];}}}return dp[nums.length-1][size];}
2.一维滚动数组——存储压缩
- dp[j]表示装满大小为j的背包有多少种方式。
- 递推公式:dp[j]=max(dp[j],dp[j-weight[i]]+values[i])
- 初始化:右边的值总是由最左边的值推导而来,dp[0]表示使背包价值为0有多少种放置方法——要么什么也不放,要么放大小为0的物品。
- 遍历:由于以为滚动数组是二维dp数组的动态行滚动更新,所以遍历顺序总是先物品后背包。
- 注意:为了防止用同层修改过的值修改本行其他值,导致物体重复放置,故采用倒序遍历背包。
public int findTargetSumWays(int[] nums, int target) {int sum=0;for(int num:nums) sum+=num;if((sum+target)%2!=0) return 0;if((sum-target)%2!=0) return 0;if(target<0) target=-target;int size= (int)Math.ceil((float)(sum+target)/2);int dp[]=new int[size+1];//初始化Arrays.fill(dp,0);dp[0]=1;//遍历顺序for(int i=0;i< nums.length;i++){for(int j=size;j>=nums[i];j--){dp[j] += dp[j - nums[i]];}}return dp[size];}
3.分析
时间复杂度:O(
)
空间复杂度:
二维:O(n*size)
一维:O(size)
相关文章:
Leetcode 494 目标和
题意理解: 给你一个非负整数数组 nums 和一个整数 target 。 向数组中的每个整数前添加 或 - ,然后串联起所有整数,可以构造一个 表达式 : 例如,nums [2, 1] ,可以在 2 之前添加 ,在 1 之前添…...
)
Windows常用命令(文件相关、进程相关、网络相关、用户相关、特殊符号)
Windows常用命令 Windows常用命令 Windows常用命令0x01 基础操作0x02 文件操作0x03 进程操作0x04 网络相关0x05 用户相关0x06 特殊符号 0x01 基础操作 清屏:cls 关机:shutdown -s(关机)-r(重启) -f(强制)…...

摘:国六排放法规下的重型车车载终端的革新
系列文章目录 文章目录 系列文章目录一、国六排放法规下的重型车车载终端的革新二、使用步骤1.引入库2.读入数据 一、国六排放法规下的重型车车载终端的革新 添加链接描述 ascii码 二、使用步骤 1.引入库 代码如下(示例): import numpy a…...

java读取json文件并解析并修改
要在Java中读取和解析JSON文件,可以使用Java提供的JSON库,例如Jackson、Gson或JSON.simple。以下是使用Jackson库的示例代码: 首先,你需要添加Jackson库的依赖到你的项目中。如果你正在使用Maven,可以在pom.xml文件中…...

2024年前端面试中JavaScript的30个高频面试题之基础知识
中级 高级知识 充分准备你的下一个JavaScript面试,增强信心! 无论你是老手还是刚进入技术行业,这份2024年必备资源都将帮助你复习核心概念,从基本语言特性到高级主题。 在本文中,我汇总了30个最关键的JavaScript面试题以及详细的答案和代码示例。 深入探索这宝贵的收藏,以确…...

鸿蒙设备-开发板基础学习(BearPi-HM Micro)
theme: minimalism 每当学习一门新的编程语言或者上手一款新的开发板,在学习鸿蒙设备开发过程中,带大家写的第一个程序,通过这个程序,我们可以对鸿蒙设备开发的整个流程有一个初步的体验。BearPi-HM Micro开发板为例:…...

Oracle导入导出dump
创建目录: create directory *** as /bak; #***名称可以随便命名 需要手工创建/bak,并且此目录oracle用户有读取,目录地址空间要够用。 查看所有目录 select * from DBA_DIRECTORIES;---查询导入导出的目录 导入 impdp ****/**** direc…...

判断vector、string是否存在某个元素
1、string字符串中是否存在某个字符(char) string中find()返回值是字母在母串中的位置(下标索引),如果没有找到,那么会返回一个特别的标记npos。(返回值可以看成是一个int型的数) …...

C语言--结构体详解
C语言--结构体详解 1.结构体产生原因2.结构体声明2.1 结构体的声明2.2 结构体的初始化2.3结构体自引用 3.结构体内存对齐3.1 对齐规则3.2 为什么存在内存对齐3.3 修改默认对⻬数 4. 结构体传参 1.结构体产生原因 C语言将数据类型分为了两种,一种是内置类型…...
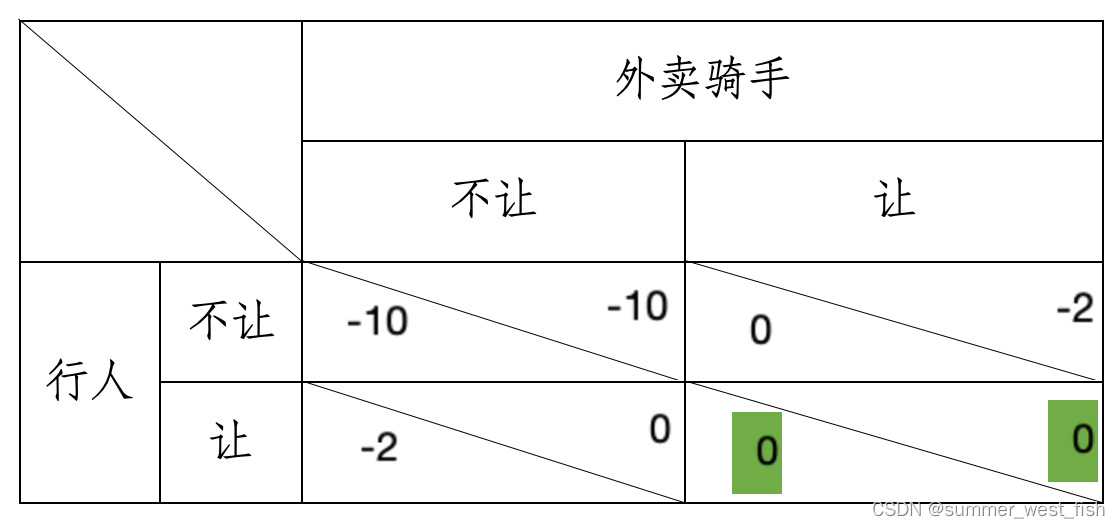
外卖骑手与行人之间的非零和博弈
一、背景 自2013年成立以来,美团外卖一直保持着高速增长,通过提供便捷、高效的外卖服务,满足了大量消费者的需求。美团外卖的服务不仅限于基础的送餐服务,还涵盖了多种生活服务,如超市便利、药品配送等,满…...
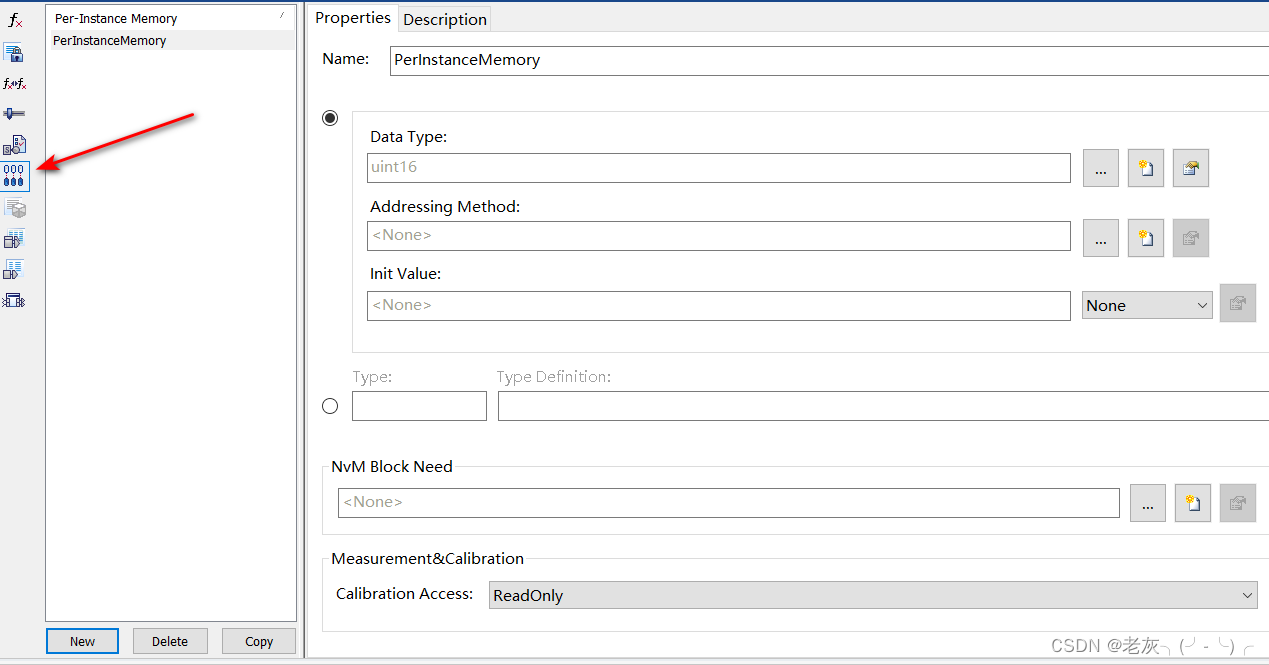
[AutoSar]基础部分 RTE 06 对runnable的触发和SWC的影响
目录 关键词平台说明一、runnable二、RTE的event2.1Mode类型event2.2周期触发类型2.3 数据交互触发 三、internal runnable value四、专属运行区指定五、per_instance memory 关键词 嵌入式、C语言、autosar、Rte 平台说明 项目ValueOSautosar OSautosar厂商vector芯片厂商T…...
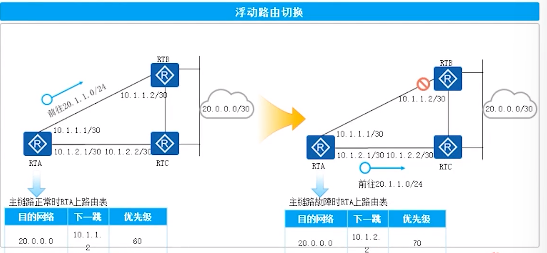
网络层协议及IP编址与IP路由基础华为ICT网络赛道
目录 4.网络层协议及IP编址 4.1.网络层协议 4.2.IPv4地址介绍 4.3.子网划分 4.4.ICMP协议 4.5.IPv4地址配置及基本应用 5.IP路由基础 5.1.路由概述 5.2.静态路由 5.3.动态路由 5.4.路由高阶特性 4.网络层协议及IP编址 4.1.网络层协议 IPv4(Internet Protocol Versi…...

基于stm32f4的蓝牙控制小车
1. 引言 蓝牙的创始人是瑞典爱立信公司,蓝牙技术是一种无限数据与语音通信的开放性全球规范,它以低成本的近距离无线连接为基础,为固定与移动设备通信环境建立一个特别连接。手机之间通过蓝牙实现数据共享成为常理,将手机变为遥…...

基于BP神经网络的租金预测
目录 摘要 BP神经网络参数设置及各种函数选择 参数设置 训练函数 传递函数 学习函数 性能函数 显示函数 前向网络创建函数 BP神经网络训练窗口详解 训练窗口例样 训练窗口四部详解 基于BP神经网络的租金预测 代码下载:基于BP神经网络的租金预测(代码完整,数据齐全)资源-CS…...
)
C语言学习记录—进阶作业(通讯录文件版本)
通讯录 1. 添加一个函数,在退出通讯录的时候把信息到保存到文件中 2. 添加一个函数,在通讯录打开的时候,可以把文件中的信息加载到通讯录中 contact.h文件 #pragma once #include <string.h> #include <stdio.h> #include <…...
深度学习笔记(四)——TF2构建基础网络常用函数+简单ML分类网络实现
文中程序以Tensorflow-2.6.0为例 部分概念包含笔者个人理解,如有遗漏或错误,欢迎评论或私信指正。 截图和程序部分引用自北京大学机器学习公开课 TF2基础常用函数 1、张量处理类 强制数据类型转换: a1 tf.constant([1,2,3], dtypetf.floa…...

GPT function calling v2
原文:GPT function calling v2 - 知乎 OpenAI在2023年11月10号举行了第一次开发者大会(OpenAI DevDays),其中介绍了很多新奇有趣的新功能和新应用,而且更新了一波GPT的API,在1.0版本后的API调用与之前的0.…...
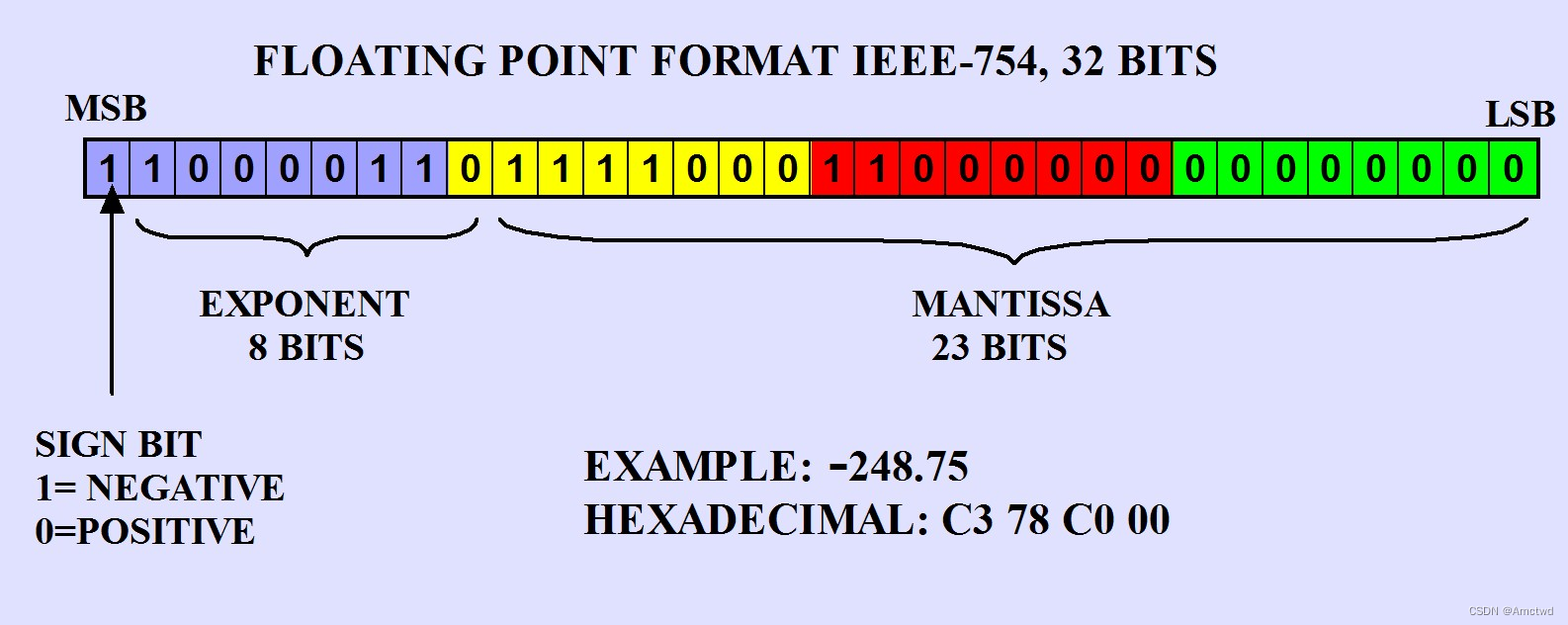
【Golang】IEEE754标准二进制字符串转为浮点类型
IEEE754介绍 IEEE 754是一种标准,用于表示和执行浮点数运算的方法。在这个标准中,单精度浮点数使用32位二进制表示,分为三个部分:符号位、指数位和尾数位。 符号位(s)用一个位来表示数的正负,0表示正数,1表…...
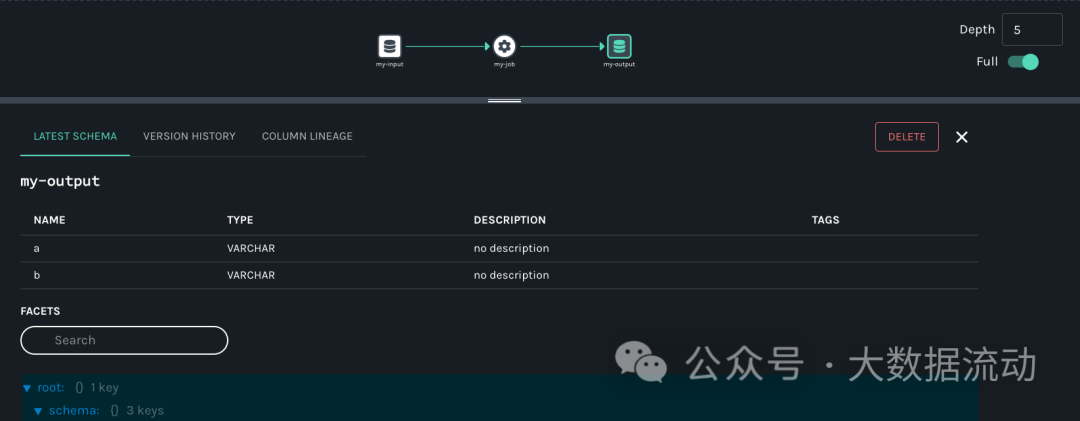
【开源项目】轻量元数据管理解决方案——Marquez
大家好,我是独孤风。 又到了本周的开源项目推荐。最近推荐的元数据管理项目很多,但是很多元数据管理平台的功能复杂难用。 那么有没有轻量一点的元数据管理项目呢? 今天为大家推荐的开源项目,就是一个轻量级的元数据管理工具。虽然…...

dirty file page
转自:https://www.cnblogs.com/zhiminyu/p/17330763.html 0.前言 Linux 内核Page Cache 和Buffer Cache 关系及演化历史 一文中讲过Linux 2.4之后将Page Cache和Buffer Cache 进行了融合,在buffer_head 中添加了b_page,很容易就能找到缓存的…...

生成xcframework
打包 XCFramework 的方法 XCFramework 是苹果推出的一种多平台二进制分发格式,可以包含多个架构和平台的代码。打包 XCFramework 通常用于分发库或框架。 使用 Xcode 命令行工具打包 通过 xcodebuild 命令可以打包 XCFramework。确保项目已经配置好需要支持的平台…...

java_网络服务相关_gateway_nacos_feign区别联系
1. spring-cloud-starter-gateway 作用:作为微服务架构的网关,统一入口,处理所有外部请求。 核心能力: 路由转发(基于路径、服务名等)过滤器(鉴权、限流、日志、Header 处理)支持负…...

Opencv中的addweighted函数
一.addweighted函数作用 addweighted()是OpenCV库中用于图像处理的函数,主要功能是将两个输入图像(尺寸和类型相同)按照指定的权重进行加权叠加(图像融合),并添加一个标量值&#x…...

cf2117E
原题链接:https://codeforces.com/contest/2117/problem/E 题目背景: 给定两个数组a,b,可以执行多次以下操作:选择 i (1 < i < n - 1),并设置 或,也可以在执行上述操作前执行一次删除任意 和 。求…...

Neo4j 集群管理:原理、技术与最佳实践深度解析
Neo4j 的集群技术是其企业级高可用性、可扩展性和容错能力的核心。通过深入分析官方文档,本文将系统阐述其集群管理的核心原理、关键技术、实用技巧和行业最佳实践。 Neo4j 的 Causal Clustering 架构提供了一个强大而灵活的基石,用于构建高可用、可扩展且一致的图数据库服务…...

EtherNet/IP转DeviceNet协议网关详解
一,设备主要功能 疆鸿智能JH-DVN-EIP本产品是自主研发的一款EtherNet/IP从站功能的通讯网关。该产品主要功能是连接DeviceNet总线和EtherNet/IP网络,本网关连接到EtherNet/IP总线中做为从站使用,连接到DeviceNet总线中做为从站使用。 在自动…...

selenium学习实战【Python爬虫】
selenium学习实战【Python爬虫】 文章目录 selenium学习实战【Python爬虫】一、声明二、学习目标三、安装依赖3.1 安装selenium库3.2 安装浏览器驱动3.2.1 查看Edge版本3.2.2 驱动安装 四、代码讲解4.1 配置浏览器4.2 加载更多4.3 寻找内容4.4 完整代码 五、报告文件爬取5.1 提…...

AI,如何重构理解、匹配与决策?
AI 时代,我们如何理解消费? 作者|王彬 封面|Unplash 人们通过信息理解世界。 曾几何时,PC 与移动互联网重塑了人们的购物路径:信息变得唾手可得,商品决策变得高度依赖内容。 但 AI 时代的来…...

html css js网页制作成品——HTML+CSS榴莲商城网页设计(4页)附源码
目录 一、👨🎓网站题目 二、✍️网站描述 三、📚网站介绍 四、🌐网站效果 五、🪓 代码实现 🧱HTML 六、🥇 如何让学习不再盲目 七、🎁更多干货 一、👨…...

基于TurtleBot3在Gazebo地图实现机器人远程控制
1. TurtleBot3环境配置 # 下载TurtleBot3核心包 mkdir -p ~/catkin_ws/src cd ~/catkin_ws/src git clone -b noetic-devel https://github.com/ROBOTIS-GIT/turtlebot3.git git clone -b noetic https://github.com/ROBOTIS-GIT/turtlebot3_msgs.git git clone -b noetic-dev…...
