代码随想录算法训练营第24天 | 理论基础 77. 组合
目录
理论基础
什么是回溯法
回溯法的效率
回溯法解决的问题
如何理解回溯法
回溯法模板
77. 组合
💡解题思路
💻实现代码
理论基础
什么是回溯法
回溯法也可以叫做回溯搜索法,它是一种搜索的方式。
回溯法的效率
虽然回溯法很难,很不好理解,但是回溯法并不是什么高效的算法。
因为回溯的本质是穷举,穷举所有可能,然后选出我们想要的答案,如果想让回溯法高效一些,可以加一些剪枝的操作,但也改不了回溯法就是穷举的本质。
那么既然回溯法并不高效为什么还要用它呢?
因为没得选,一些问题能暴力搜出来就不错了,撑死了再剪枝一下,还没有更高效的解法。
回溯法解决的问题
回溯法,一般可以解决如下几种问题:
- 组合问题:N个数里面按一定规则找出k个数的集合
- 切割问题:一个字符串按一定规则有几种切割方式
- 子集问题:一个N个数的集合里有多少符合条件的子集
- 排列问题:N个数按一定规则全排列,有几种排列方式
- 棋盘问题:N皇后,解数独等等
组合是不强调元素顺序的,排列是强调元素顺序。
例如:{1, 2} 和 {2, 1} 在组合上,就是一个集合,因为不强调顺序,而要是排列的话,{1, 2} 和 {2, 1} 就是两个集合了。
记住组合无序,排列有序,就可以了。
如何理解回溯法
回溯法解决的问题都可以抽象为树形结构,是的,我指的是所有回溯法的问题都可以抽象为树形结构!
因为回溯法解决的都是在集合中递归查找子集,集合的大小就构成了树的宽度,递归的深度,都构成的树的深度。
递归就要有终止条件,所以必然是一棵高度有限的树(N叉树)。
回溯法模板
- 回溯函数模板返回值以及参数
在回溯算法中,我的习惯是函数起名字为backtracking,这个起名大家随意。回溯算法中函数返回值一般为void。
回溯函数伪代码如下:
void backtracking(参数)
- 回溯函数终止条件
什么时候达到了终止条件,树中就可以看出,一般来说搜到叶子节点了,也就找到了满足条件的一条答案,把这个答案存放起来,并结束本层递归。
所以回溯函数终止条件伪代码如下:
if (终止条件) {存放结果;return;
}
- 回溯搜索的遍历过程
在上面我们提到了,回溯法一般是在集合中递归搜索,集合的大小构成了树的宽度,递归的深度构成的树的深度。
如图:
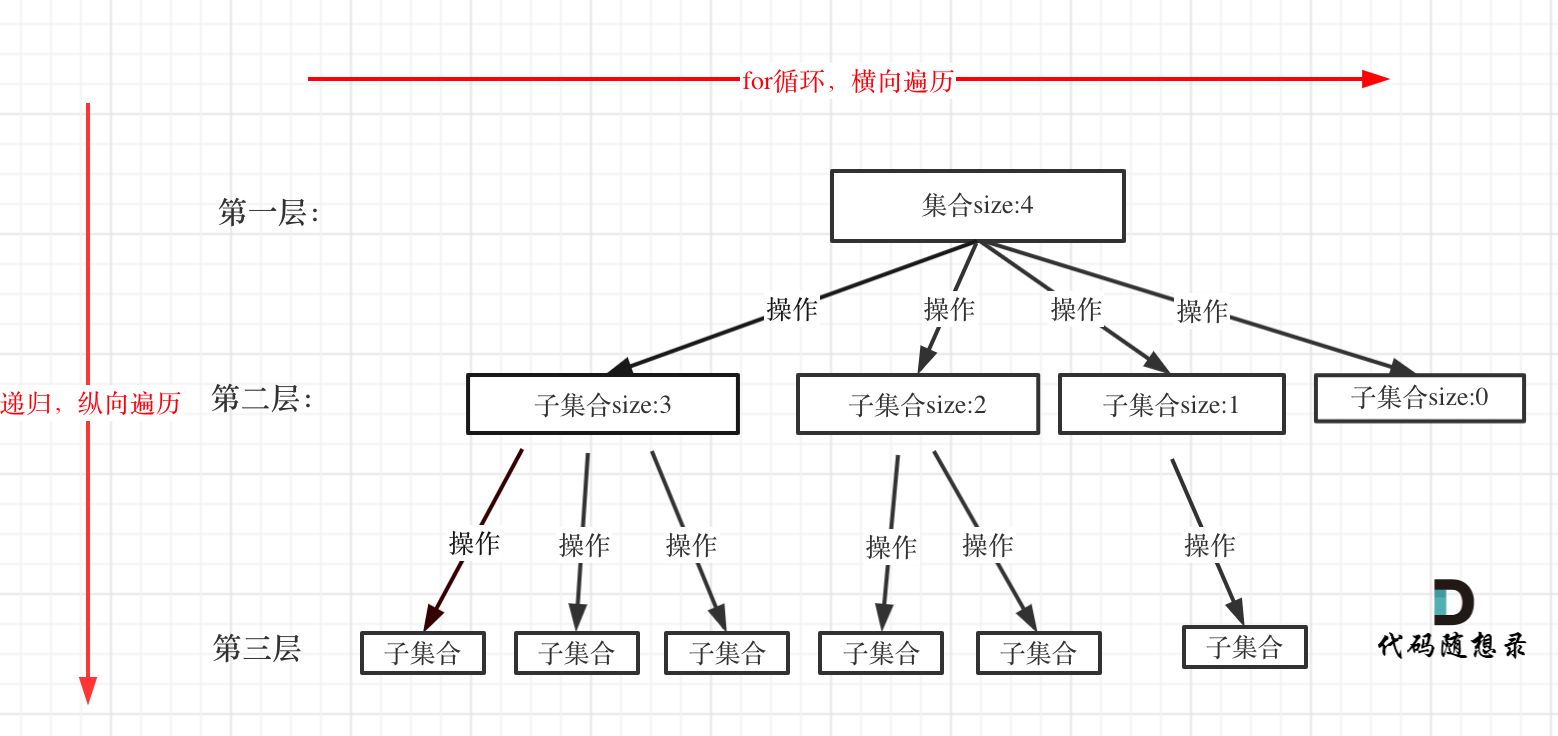
注意图中,我特意举例集合大小和孩子的数量是相等的!
回溯函数遍历过程伪代码如下:
for (选择:本层集合中元素(树中节点孩子的数量就是集合的大小)) {处理节点;backtracking(路径,选择列表); // 递归回溯,撤销处理结果
}
for循环就是遍历集合区间,可以理解一个节点有多少个孩子,这个for循环就执行多少次。
backtracking这里自己调用自己,实现递归。
大家可以从图中看出for循环可以理解是横向遍历,backtracking(递归)就是纵向遍历,这样就把这棵树全遍历完了,一般来说,搜索叶子节点就是找的其中一个结果了。
分析完过程,回溯算法模板框架如下:
void backtracking(参数) {if (终止条件) {存放结果;return;}for (选择:本层集合中元素(树中节点孩子的数量就是集合的大小)) {处理节点;backtracking(路径,选择列表); // 递归回溯,撤销处理结果}
}77. 组合
题目链接:77.组合
给定两个整数 n 和 k,返回 1 ... n 中所有可能的 k 个数的组合。
示例: 输入: n = 4, k = 2 输出: [ [2,4], [3,4], [2,3], [1,2], [1,3], [1,4], ]
💡解题思路
把组合问题抽象为如下树形结构:
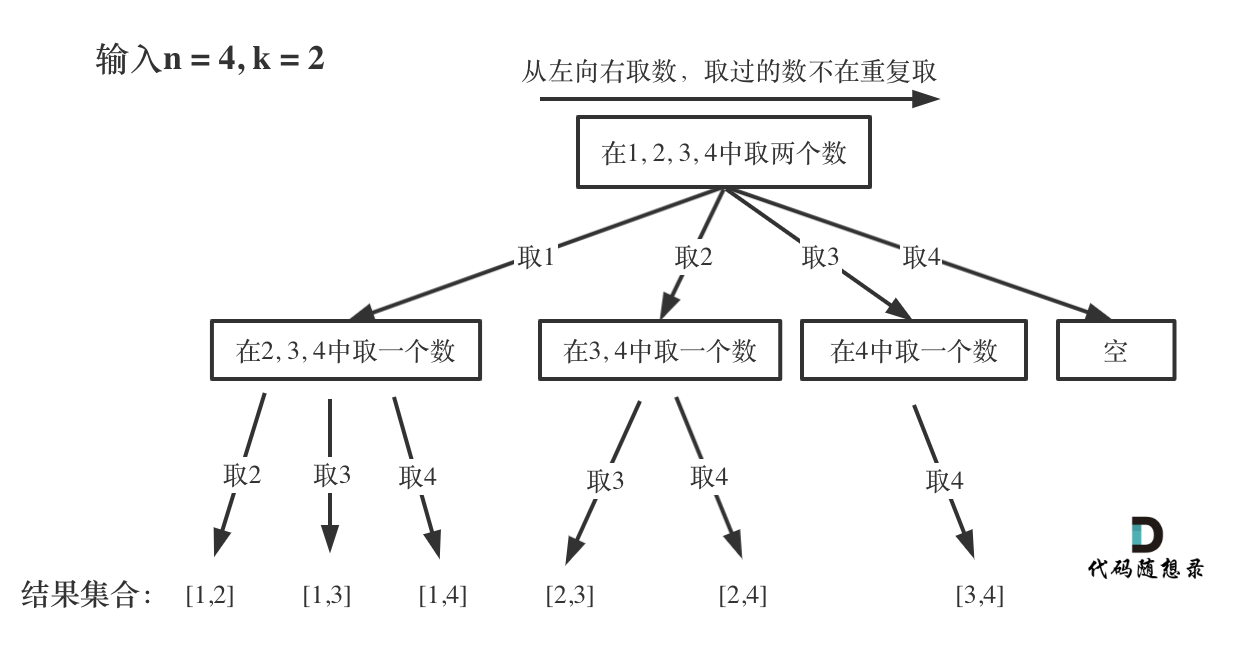
可以看出这棵树,一开始集合是 1,2,3,4, 从左向右取数,取过的数,不再重复取。
第一次取1,集合变为2,3,4 ,因为k为2,我们只需要再取一个数就可以了,分别取2,3,4,得到集合[1,2] [1,3] [1,4],以此类推。
每次从集合中选取元素,可选择的范围随着选择的进行而收缩,调整可选择的范围。
图中可以发现n相当于树的宽度,k相当于树的深度。
那么如何在这个树上遍历,然后收集到我们要的结果集呢?
图中每次搜索到了叶子节点,我们就找到了一个结果。
相当于只需要把达到叶子节点的结果收集起来,就可以求得 n个数中k个数的组合集合。
💻实现代码
class Solution {List<List<Integer>> res =new ArrayList<>();LinkedList<Integer> path =new LinkedList<>();public List<List<Integer>> combine(int n, int k) {backtracking(n,k,1);return res;}private void backtracking(int n,int k,int startIndex){if(path.size()==k){res.add(new ArrayList<>(path));return;}for(int i=startIndex;i<=n-(k-path.size())+1;i++){path.add(i);backtracking(n,k,i+1);path.removeLast();}}
}相关文章:

代码随想录算法训练营第24天 | 理论基础 77. 组合
目录 理论基础 什么是回溯法 回溯法的效率 回溯法解决的问题 如何理解回溯法 回溯法模板 77. 组合 💡解题思路 💻实现代码 理论基础 什么是回溯法 回溯法也可以叫做回溯搜索法,它是一种搜索的方式。 回溯法的效率 虽然回溯法很难ÿ…...

【深度学习环境搭建】Windows搭建Anaconda3、已经Pytorch的GPU版本
目录 搭建Anaconda3搭建GPU版本的Pytorch你的pip也要换源,推荐阿里源打开conda的PowerShell验证 搭建Anaconda3 无脑下载安装包安装(自行百度) 注意点: 1、用户目录下的.condarc需要配置(自定义环境的地址(…...

基于WebFlux的Websocket的实现,高级实现自定义功能拓展
基于WebFlux的Websocket 一、导入XML依赖 <dependency><groupId>org.springframework.boot</groupId><artifactId>spring-boot-starter-webflux</artifactId> </dependency><!-- 或者引入jackson --> <dependency><group…...

使用 LLVM clang C/C++ 编译器编译 OpenSSL 3.X库
1、下载 OpenSSL 3.X 库的源代码放到待编译目录 2、解压并接入 OpenSSL 3.X 库源码的根目录 3、复制 ./Configure 一个取名为 ./Configure-clang 4、修改 ./Configure-clang 找到配置段: CC CXX CPP LD 把它们改成 CC > "/usr/bin/clang-…...

【信息安全】hydra爆破工具的使用方法
hydra简介 hydra又名九头蛇,与burp常规的爆破模块不同,hydra爆破的范围更加广泛,可以爆破远程桌面连接,数据库这类的密码。他在kali系统中自带。 参数说明 -l 指定用户名 -L 指定用户名字典文件 -p 指定密码 -P 指…...

uniapp中uview组件库丰富的CountTo 数字滚动使用方法
目录 #平台差异说明 #基本使用 #设置滚动相关参数 #是否显示小数位 #千分位分隔符 #滚动执行的时机 #API #Props #Methods #Event 该组件一般用于需要滚动数字到某一个值的场景,目标要求是一个递增的值。 注意 如果给组件的父元素设置text-align: cente…...

inflate流程分析
一.inflate的三参数重载方法else里面逻辑 我们先看到setContentView里面的inflate的调用链: public View inflate(LayoutRes int resource, Nullable ViewGroup root) {return inflate(resource, root, root ! null);}public View inflate(LayoutRes int resource…...

数据挖掘实战-基于机器学习的电商文本分类模型
🤵♂️ 个人主页:艾派森的个人主页 ✍🏻作者简介:Python学习者 🐋 希望大家多多支持,我们一起进步!😄 如果文章对你有帮助的话, 欢迎评论 💬点赞Ǵ…...
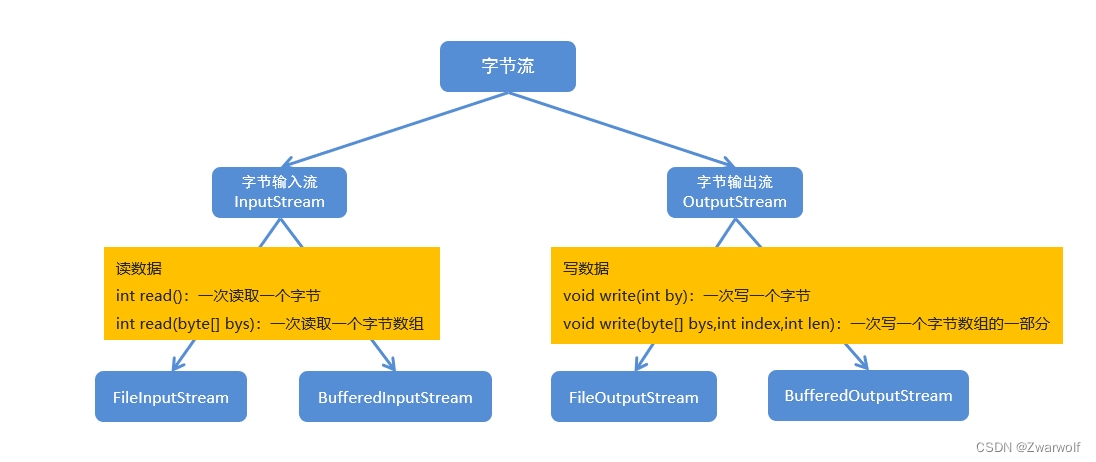
第8章-第4节-Java中字节流的缓冲流
1、缓冲流:属于高级IO流,并不能直接读写数据,需要依赖于基础流。缓冲流的目的是为了提高文件的读写效率?那么是如何提高文件的读写效率的呢? 在内存中设置一个缓冲区,缓冲区的默认大小是8192字节ÿ…...

NULL是什么?
NULL是一个编程术语,通常用于表示一个空值或无效值。在很多编程语言中,NULL用于表示一个变量或指针不引用任何有效的对象或内存位置。 NULL可以看作是一个特殊的值,表示缺少有效的数据或引用。当一个变量被赋予NULL值时,它表示该变…...

FreeRTOS 基础知识
这个基础知识也是非常重要的,那我们要学好 FreeRTOS,这些都是必不可少的。 那么就来看一下本节有哪些内容: 首先呢就是介绍一下什么是任务调度器。接着呢就是任务它拥有哪一些状态了。那这里的内容不多,但是呢都是非常重要的。 …...
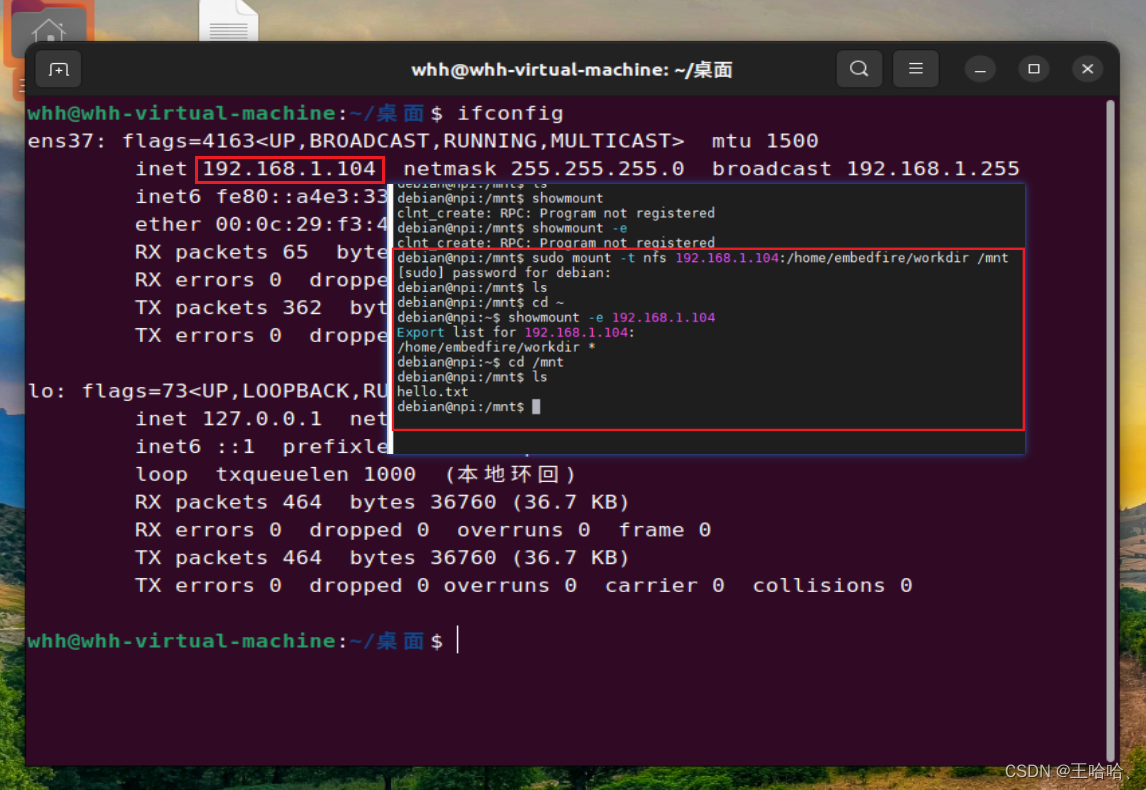
【野火i.MX6NULL开发板】挂载 NFS 网络文件系统
0、前言 参考资料: (误人子弟)《野火 Linux 基础与应用开发实战指南基于 i.MX6ULL 系列》PDF 第22章 参考视频:(成功) https://www.bilibili.com/video/BV1JK4y1t7io?p26&vd_sourcefb8dcae0aee3f1aab…...
方法或展开语法(...)来合并对象,Object.freeze()方法来冻结对象,防止对象被修改)
在JavaScript中,Object.assign()方法或展开语法(...)来合并对象,Object.freeze()方法来冻结对象,防止对象被修改
文章目录 一、Object.freeze()方法来冻结对象,防止对象被修改1、基本使用2、冻结数组2.1、浅冻结2.1、深冻结 3、应用场景4、Vue中使用Object.freeze 二、Object.assign()方法或展开语法(...)来合并对象1、Object.assign()1.1、语法1.2、参数…...
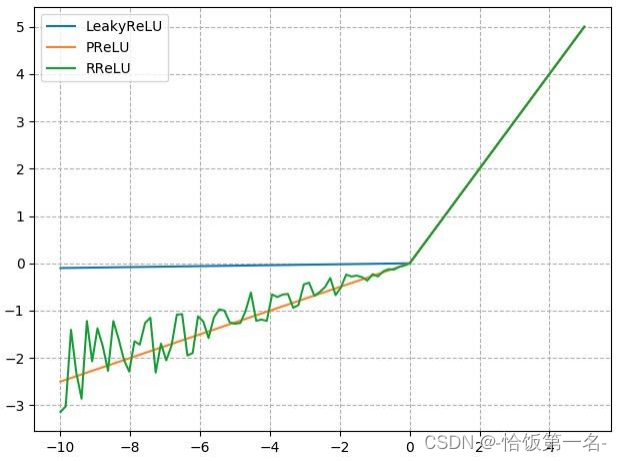
池化、线性、激活函数层
一、池化层 池化运算是深度学习中常用的一种操作,它可以对输入的特征图进行降采样,从而减少特征图的尺寸和参数数量。 池化运算的主要目的是通过“收集”和“总结”输入特征图的信息来提取出主要特征,并且减少对细节的敏感性。在池化运算中…...
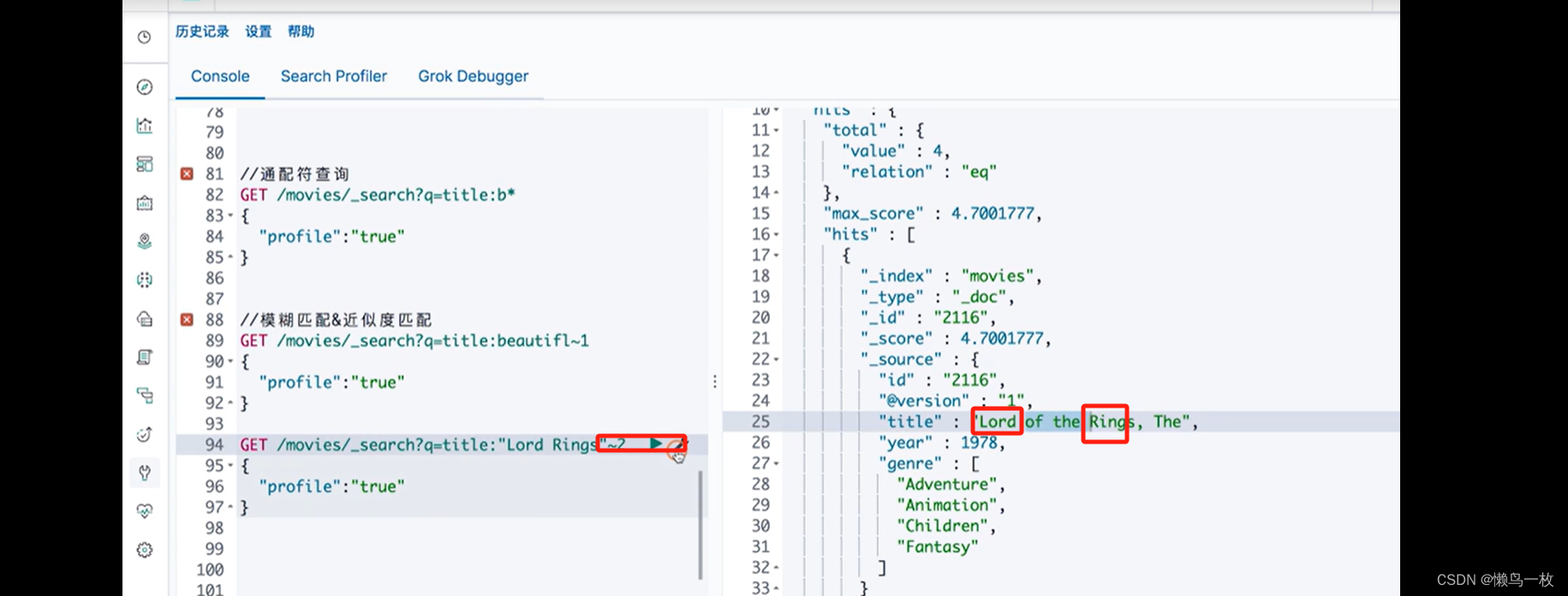
ES-极客学习第二部分ES 入门
基本概念 索引、文档、节点、分片和API json 文档 文档的元数据 需要通过Kibana导入Sample Data的电商数据。具体参考“2.2节-Kibana的安装与界面快速浏览” 索引 kibana 管理ES索引 在系统中找到kibana配置文件(我这里是etc/kibana/kibana.yml) vim /…...

Nodejs软件安装
Nodejs软件安装 一、简介 Node.js 是一个基于 Chrome V8 引擎的 JavaScript 运行环境。 官网:http://nodejs.cn/api/ 我们关注于 node.js 的 npm 功能,NPM 是随同 NodeJS 一起安装的包管理工具,JavaScript-NPM,Java-Maven&…...
Photoshop 2024 (PS2024) v25 直装版 支持win/mac版
Photoshop 2024 提供了多种创意工具,如画笔、铅笔、涂鸦和渐变等,用户可以通过这些工具来创建独特和令人印象深刻的设计效果。增强的云同步:通过 Adobe Creative Cloud,用户可以方便地将他们的工作从一个设备无缝同步到另一个设备…...

ChatGPT绘画生成软件MidTool:智能艺术的新纪元
在人工智能的黄金时代,创新技术不断涌现,改变着我们的生活和工作方式。其中,ChatGPT绘画生成软件MidTool无疑是这一变革浪潮中的佼佼者。它不仅是一个软件,更是一位艺术家,一位智能助手,它的出现预示着智能…...

linux安装MySQL5.7(安装、开机自启、定时备份)
一、安装步骤 我喜欢安装在/usr/local/mysql目录下 #切换目录 cd /usr/local/ #下载文件 wget https://dev.mysql.com/get/Downloads/MySQL-5.7/mysql-5.7.38-linux-glibc2.12-x86_64.tar.gz #解压文件 tar -zxvf mysql-5.7.38-linux-glibc2.12-x86_64.tar.gz -C /usr/local …...

openGauss学习笔记-195 openGauss 数据库运维-常见故障定位案例-分析查询语句运行状态
文章目录 openGauss学习笔记-195 openGauss 数据库运维-常见故障定位案例-分析查询语句运行状态195.1 分析查询语句运行状态195.1.1 问题现象195.1.2 处理办法 openGauss学习笔记-195 openGauss 数据库运维-常见故障定位案例-分析查询语句运行状态 195.1 分析查询语句运行状态…...

国防科技大学计算机基础课程笔记02信息编码
1.机内码和国标码 国标码就是我们非常熟悉的这个GB2312,但是因为都是16进制,因此这个了16进制的数据既可以翻译成为这个机器码,也可以翻译成为这个国标码,所以这个时候很容易会出现这个歧义的情况; 因此,我们的这个国…...
)
React Native 开发环境搭建(全平台详解)
React Native 开发环境搭建(全平台详解) 在开始使用 React Native 开发移动应用之前,正确设置开发环境是至关重要的一步。本文将为你提供一份全面的指南,涵盖 macOS 和 Windows 平台的配置步骤,如何在 Android 和 iOS…...

Oracle查询表空间大小
1 查询数据库中所有的表空间以及表空间所占空间的大小 SELECTtablespace_name,sum( bytes ) / 1024 / 1024 FROMdba_data_files GROUP BYtablespace_name; 2 Oracle查询表空间大小及每个表所占空间的大小 SELECTtablespace_name,file_id,file_name,round( bytes / ( 1024 …...

【AI学习】三、AI算法中的向量
在人工智能(AI)算法中,向量(Vector)是一种将现实世界中的数据(如图像、文本、音频等)转化为计算机可处理的数值型特征表示的工具。它是连接人类认知(如语义、视觉特征)与…...

12.找到字符串中所有字母异位词
🧠 题目解析 题目描述: 给定两个字符串 s 和 p,找出 s 中所有 p 的字母异位词的起始索引。 返回的答案以数组形式表示。 字母异位词定义: 若两个字符串包含的字符种类和出现次数完全相同,顺序无所谓,则互为…...

如何在最短时间内提升打ctf(web)的水平?
刚刚刷完2遍 bugku 的 web 题,前来答题。 每个人对刷题理解是不同,有的人是看了writeup就等于刷了,有的人是收藏了writeup就等于刷了,有的人是跟着writeup做了一遍就等于刷了,还有的人是独立思考做了一遍就等于刷了。…...

React---day11
14.4 react-redux第三方库 提供connect、thunk之类的函数 以获取一个banner数据为例子 store: 我们在使用异步的时候理应是要使用中间件的,但是configureStore 已经自动集成了 redux-thunk,注意action里面要返回函数 import { configureS…...

【 java 虚拟机知识 第一篇 】
目录 1.内存模型 1.1.JVM内存模型的介绍 1.2.堆和栈的区别 1.3.栈的存储细节 1.4.堆的部分 1.5.程序计数器的作用 1.6.方法区的内容 1.7.字符串池 1.8.引用类型 1.9.内存泄漏与内存溢出 1.10.会出现内存溢出的结构 1.内存模型 1.1.JVM内存模型的介绍 内存模型主要分…...

基于PHP的连锁酒店管理系统
有需要请加文章底部Q哦 可远程调试 基于PHP的连锁酒店管理系统 一 介绍 连锁酒店管理系统基于原生PHP开发,数据库mysql,前端bootstrap。系统角色分为用户和管理员。 技术栈 phpmysqlbootstrapphpstudyvscode 二 功能 用户 1 注册/登录/注销 2 个人中…...

OD 算法题 B卷【正整数到Excel编号之间的转换】
文章目录 正整数到Excel编号之间的转换 正整数到Excel编号之间的转换 excel的列编号是这样的:a b c … z aa ab ac… az ba bb bc…yz za zb zc …zz aaa aab aac…; 分别代表以下的编号1 2 3 … 26 27 28 29… 52 53 54 55… 676 677 678 679 … 702 703 704 705;…...
