力扣:209.长度最小的子数组
1.题目分析:
给定一个含有 n 个正整数的数组和一个正整数 target 。
找出该数组中满足其总和大于等于 target 的长度最小的 连续子数组 [numsl, numsl+1, ..., numsr-1, numsr] ,并返回其长度。如果不存在符合条件的子数组,返回 0 。
示例 1:
输入:target = 7, nums = [2,3,1,2,4,3] 输出:2 解释:子数组 [4,3]是该条件下的长度最小的子数组。
1.找出连续子数组
2.最短长度
3.特殊情况:数组总和小于target,返回零
2.算法分析:
方法一:暴力枚举:时间复杂度是O(n^3)
设置两个指针,分别表示子数组的开始和子数组的结束两层for循环,最后求子数组总和一个while,自己在脑子想想,跑不过,我就不画图,写代码了哈。
方法二:在暴力枚举的方法上做出改进-->滑动窗口,还是用了双指针,和单调性,全是正数会越加越大,让两个指针同向移动来实现优化
滑动窗口步骤:1.进入窗口
2.判断窗口
3.退出窗口
例一图示(target = 7, nums = [2,3,1,2,4,3]):
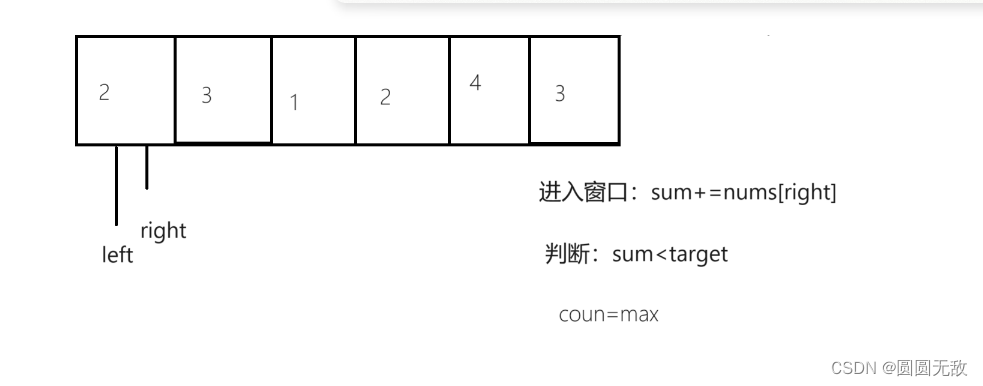



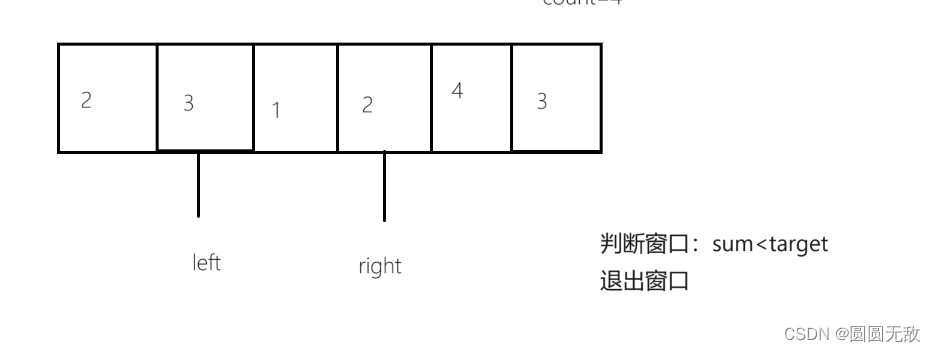


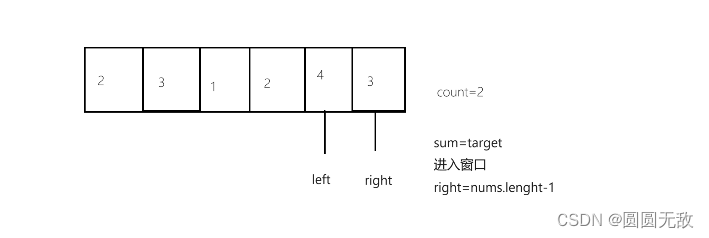
3.代码编写:
public static int minSubArrayLen(int target, int[] nums) {int sum=0;int count=Integer.MAX_VALUE;int left=0;int right=0;for(left=0,right=0;right<nums.length;right++){sum+=nums[right];//进窗口while (sum>=target)//判断{count=Math.min(count,right-left+1);sum-=nums[left++];//出窗口}}if(count==Integer.MAX_VALUE){return 0;}return count;}
相关文章:

力扣:209.长度最小的子数组
1.题目分析: 给定一个含有 n 个正整数的数组和一个正整数 target 。 找出该数组中满足其总和大于等于 target 的长度最小的 连续子数组 [numsl, numsl1, ..., numsr-1, numsr] ,并返回其长度。如果不存在符合条件的子数组,返回 0 。 示例 …...

常见类型的yaml文件如何编写?--kind: Service
基本说明 在 Kubernetes 中,Service 是一种抽象的方式,用于定义一组 Pod 的访问方式和网络服务。Service 提供了一个稳定的网络端点(Endpoint),使得其他服务或外部用户可以通过 Service 来访问被管理的 Pod。 负载均…...

linux环境下安装postgresql
PostgreSQL: Linux downloads (Red Hat family)postgresql官网 PostgreSQL: Linux downloads (Red Hat family) 环境: centos7 postgresql14 选择版本 执行启动命令 配置远程连接文件 vi /var/lib/pqsql/14/data/postgresql.conf 这里将listen_addresses值由lo…...

专业课145+合肥工业大学833信号分析与处理考研经验合工大电子信息通信
今年专业课145也是考研科目中最满意的一门,其他基本相对平平,所以这里我总结一下自己的专业课合肥工业大学833信号分析与处理的复习经验。 我所用的教材是郑君里的《信号与系统》(第三版)和高西全、丁玉美的《数字信号处理》&…...
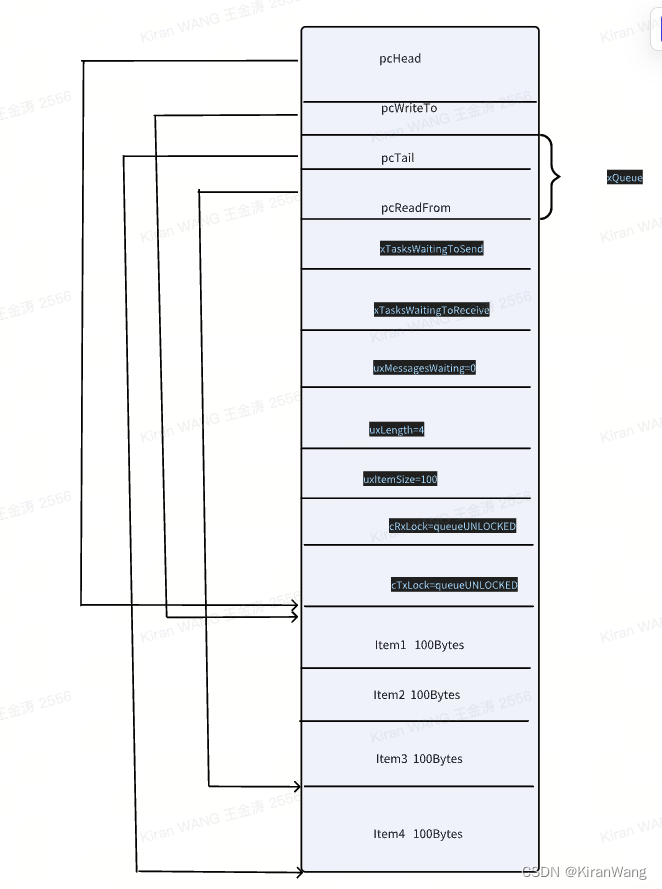
FreeRtos Queue (一)
本篇主要讲队列的数据结构和初始化 一、队列的数据结构 二、队列初始化完是什么样子的 队列初始化的函数调用关系:xQueueGenericCreate->prvInitialiseNewQueue->xQueueGenericReset 所以,最终初始化完的队列是这样的 假设申请了4个消息体&…...
深入理解 Hadoop (五)YARN核心工作机制浅析
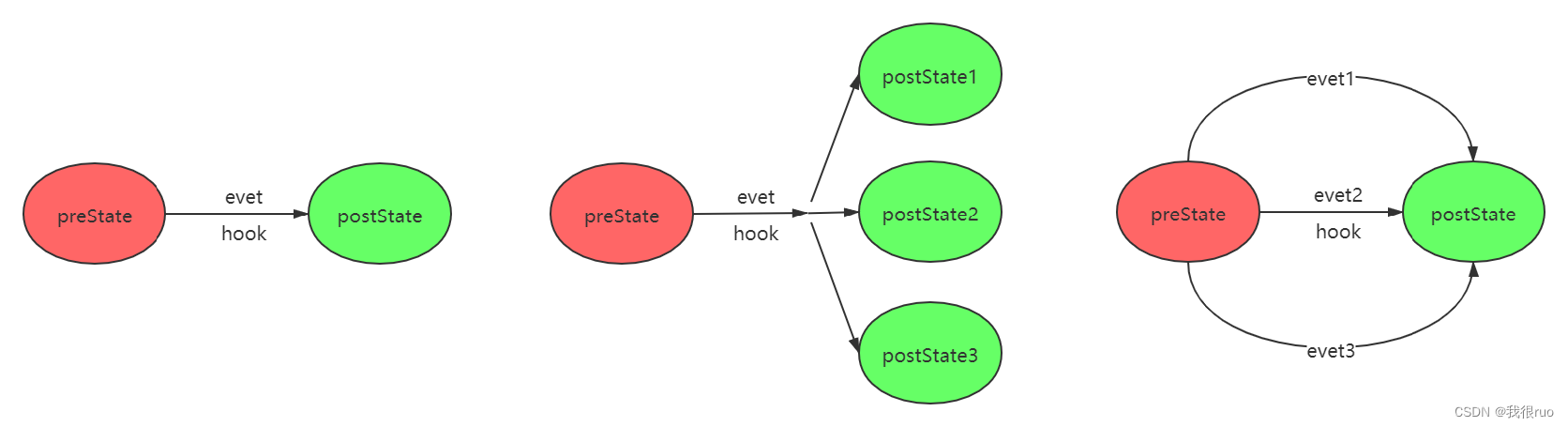
概述 YARN 的核心设计理念是 服务化(Service) 和 事件驱动(Event EventHandler)。服务化 和 事件驱动 软件设计思想的引入,使得 YARN 具有低耦合、高内聚的特点,各个模块只需完成各自功能,而模…...

优化 - 重构一次Mysql导致服务器的OOM
概述 优化了一次前后端处理不当导致的CPU的一次爆机行为,当然,这和服务器的配置低也有着密不可分的关系,简单的逻辑学告诉我们,要找到真正的问题,进行解决,CPU爆机的关键点在于前后端两个方面,…...

【光波电子学】基于MATLAB的多模光纤模场分布的仿真分析
基于MATLAB的多模光纤模场分布的仿真分析 一、引言 (1)多模光纤的概念 多模光纤(MMF)是一种具有较大纤芯直径的光纤结构,其核心直径通常在10-50微米范围内。与单模光纤(SMF)相比,…...

0104 AJAX介绍
Ajax 的全称是 Asynchronous Javascript And XML (异步 JavaScript 和 XML )。 通俗的理解:在网页中利用 XMLHttpRequest 对象和服务器进行数据交互的方式,就是 Ajax Ajax 能让我们轻松实现网页与服务器之间的数据交互。 浏览器…...
代码随想录算法训练营第24天 | 理论基础 77. 组合
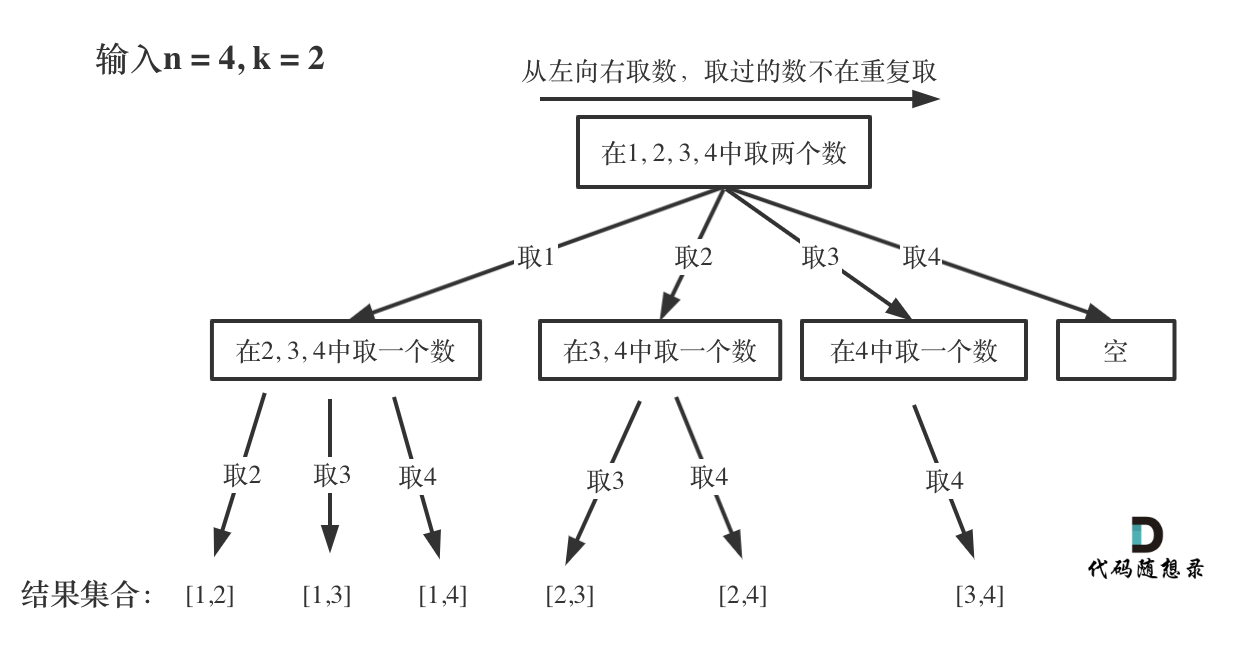
目录 理论基础 什么是回溯法 回溯法的效率 回溯法解决的问题 如何理解回溯法 回溯法模板 77. 组合 💡解题思路 💻实现代码 理论基础 什么是回溯法 回溯法也可以叫做回溯搜索法,它是一种搜索的方式。 回溯法的效率 虽然回溯法很难ÿ…...

【深度学习环境搭建】Windows搭建Anaconda3、已经Pytorch的GPU版本
目录 搭建Anaconda3搭建GPU版本的Pytorch你的pip也要换源,推荐阿里源打开conda的PowerShell验证 搭建Anaconda3 无脑下载安装包安装(自行百度) 注意点: 1、用户目录下的.condarc需要配置(自定义环境的地址(…...

基于WebFlux的Websocket的实现,高级实现自定义功能拓展
基于WebFlux的Websocket 一、导入XML依赖 <dependency><groupId>org.springframework.boot</groupId><artifactId>spring-boot-starter-webflux</artifactId> </dependency><!-- 或者引入jackson --> <dependency><group…...

使用 LLVM clang C/C++ 编译器编译 OpenSSL 3.X库
1、下载 OpenSSL 3.X 库的源代码放到待编译目录 2、解压并接入 OpenSSL 3.X 库源码的根目录 3、复制 ./Configure 一个取名为 ./Configure-clang 4、修改 ./Configure-clang 找到配置段: CC CXX CPP LD 把它们改成 CC > "/usr/bin/clang-…...

【信息安全】hydra爆破工具的使用方法
hydra简介 hydra又名九头蛇,与burp常规的爆破模块不同,hydra爆破的范围更加广泛,可以爆破远程桌面连接,数据库这类的密码。他在kali系统中自带。 参数说明 -l 指定用户名 -L 指定用户名字典文件 -p 指定密码 -P 指…...

uniapp中uview组件库丰富的CountTo 数字滚动使用方法
目录 #平台差异说明 #基本使用 #设置滚动相关参数 #是否显示小数位 #千分位分隔符 #滚动执行的时机 #API #Props #Methods #Event 该组件一般用于需要滚动数字到某一个值的场景,目标要求是一个递增的值。 注意 如果给组件的父元素设置text-align: cente…...

inflate流程分析
一.inflate的三参数重载方法else里面逻辑 我们先看到setContentView里面的inflate的调用链: public View inflate(LayoutRes int resource, Nullable ViewGroup root) {return inflate(resource, root, root ! null);}public View inflate(LayoutRes int resource…...

数据挖掘实战-基于机器学习的电商文本分类模型
🤵♂️ 个人主页:艾派森的个人主页 ✍🏻作者简介:Python学习者 🐋 希望大家多多支持,我们一起进步!😄 如果文章对你有帮助的话, 欢迎评论 💬点赞Ǵ…...
第8章-第4节-Java中字节流的缓冲流
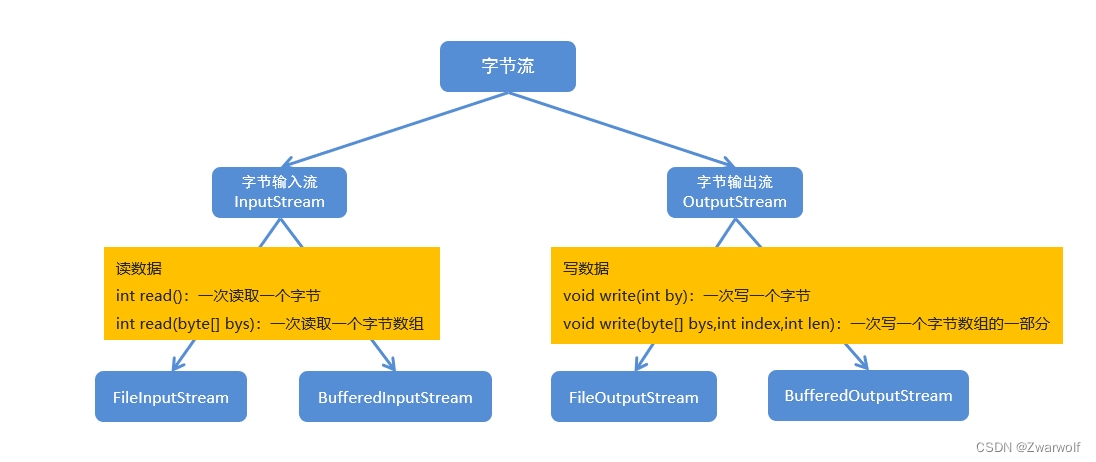
1、缓冲流:属于高级IO流,并不能直接读写数据,需要依赖于基础流。缓冲流的目的是为了提高文件的读写效率?那么是如何提高文件的读写效率的呢? 在内存中设置一个缓冲区,缓冲区的默认大小是8192字节ÿ…...

NULL是什么?
NULL是一个编程术语,通常用于表示一个空值或无效值。在很多编程语言中,NULL用于表示一个变量或指针不引用任何有效的对象或内存位置。 NULL可以看作是一个特殊的值,表示缺少有效的数据或引用。当一个变量被赋予NULL值时,它表示该变…...

FreeRTOS 基础知识
这个基础知识也是非常重要的,那我们要学好 FreeRTOS,这些都是必不可少的。 那么就来看一下本节有哪些内容: 首先呢就是介绍一下什么是任务调度器。接着呢就是任务它拥有哪一些状态了。那这里的内容不多,但是呢都是非常重要的。 …...

Ubuntu系统下交叉编译openssl
一、参考资料 OpenSSL&&libcurl库的交叉编译 - hesetone - 博客园 二、准备工作 1. 编译环境 宿主机:Ubuntu 20.04.6 LTSHost:ARM32位交叉编译器:arm-linux-gnueabihf-gcc-11.1.0 2. 设置交叉编译工具链 在交叉编译之前&#x…...

JavaScript 中的 ES|QL:利用 Apache Arrow 工具
作者:来自 Elastic Jeffrey Rengifo 学习如何将 ES|QL 与 JavaScript 的 Apache Arrow 客户端工具一起使用。 想获得 Elastic 认证吗?了解下一期 Elasticsearch Engineer 培训的时间吧! Elasticsearch 拥有众多新功能,助你为自己…...

渗透实战PortSwigger靶场-XSS Lab 14:大多数标签和属性被阻止
<script>标签被拦截 我们需要把全部可用的 tag 和 event 进行暴力破解 XSS cheat sheet: https://portswigger.net/web-security/cross-site-scripting/cheat-sheet 通过爆破发现body可以用 再把全部 events 放进去爆破 这些 event 全部可用 <body onres…...

Go 语言接口详解
Go 语言接口详解 核心概念 接口定义 在 Go 语言中,接口是一种抽象类型,它定义了一组方法的集合: // 定义接口 type Shape interface {Area() float64Perimeter() float64 } 接口实现 Go 接口的实现是隐式的: // 矩形结构体…...

蓝桥杯 2024 15届国赛 A组 儿童节快乐
P10576 [蓝桥杯 2024 国 A] 儿童节快乐 题目描述 五彩斑斓的气球在蓝天下悠然飘荡,轻快的音乐在耳边持续回荡,小朋友们手牵着手一同畅快欢笑。在这样一片安乐祥和的氛围下,六一来了。 今天是六一儿童节,小蓝老师为了让大家在节…...

CentOS下的分布式内存计算Spark环境部署
一、Spark 核心架构与应用场景 1.1 分布式计算引擎的核心优势 Spark 是基于内存的分布式计算框架,相比 MapReduce 具有以下核心优势: 内存计算:数据可常驻内存,迭代计算性能提升 10-100 倍(文档段落:3-79…...

服务器硬防的应用场景都有哪些?
服务器硬防是指一种通过硬件设备层面的安全措施来防御服务器系统受到网络攻击的方式,避免服务器受到各种恶意攻击和网络威胁,那么,服务器硬防通常都会应用在哪些场景当中呢? 硬防服务器中一般会配备入侵检测系统和预防系统&#x…...
指令的指南)
在Ubuntu中设置开机自动运行(sudo)指令的指南
在Ubuntu系统中,有时需要在系统启动时自动执行某些命令,特别是需要 sudo权限的指令。为了实现这一功能,可以使用多种方法,包括编写Systemd服务、配置 rc.local文件或使用 cron任务计划。本文将详细介绍这些方法,并提供…...

【OSG学习笔记】Day 16: 骨骼动画与蒙皮(osgAnimation)
骨骼动画基础 骨骼动画是 3D 计算机图形中常用的技术,它通过以下两个主要组件实现角色动画。 骨骼系统 (Skeleton):由层级结构的骨头组成,类似于人体骨骼蒙皮 (Mesh Skinning):将模型网格顶点绑定到骨骼上,使骨骼移动…...

深入解析C++中的extern关键字:跨文件共享变量与函数的终极指南
🚀 C extern 关键字深度解析:跨文件编程的终极指南 📅 更新时间:2025年6月5日 🏷️ 标签:C | extern关键字 | 多文件编程 | 链接与声明 | 现代C 文章目录 前言🔥一、extern 是什么?&…...
