【排序篇2】选择排序、计数排序
目录
- 一、选择排序
- 二、计数排序
一、选择排序
整体思想:
从数组中选出最小值和最大值放在起始位置,直到排序完成
具体步骤:
- 定义两个变量begin和end为下标,指向数组始末
- 定义要找的最大值的下标为maxi,最小值的下标为mini,刚开始初始化为begin,因为begin和end会缩小,也就是说找最大和最小的范围为当前begin和end之间的范围
- 找到最大值的下标和最小值的下标,然后把最小值与begin位置的值交换,这里要考虑特殊情况,最后再交换最大值和end位置的值
- begin++,end–,缩小范围再重复前面的步骤
图示:

代码:
void SelectSort(int* a, int n)
{//数组的范围int begin = 0, end = n - 1;while (begin < end)//控制范围{// maxi和mini是下标,从begin开始,因为begin会变化int maxi = begin, mini = begin;//找最大元素的下标和最小元素的下标for (int i = begin; i <= end; i++)//注意找的范围{if (a[i] > a[maxi]){maxi = i;}if (a[i] < a[mini]){mini = i;}}//最小值与begin的位置交换Swap(&a[begin], &a[mini]);//特殊情况,如果maxi与begin重叠,此时最大值的下标在miniif (begin == maxi){maxi = mini;}//最大值与end的位置交换Swap(&a[end], &a[maxi]);//缩小范围++begin;--end;}
}
特性总结:
- 时间复杂度:O(N ^ 2)
- 空间复杂度:O(1)
- 不稳定
二、计数排序
计数排序采用相对映射的思想,开辟一块空间,该空间的范围为待排序的数组的最大值和最小值之差加1,并且每个元素初始化为0,然后待排序的数组只要是出现的元素就在临时空间对应的位置计数,最后从小到大恢复原来的元素重新放入数组,完成排序。
思路:
- 在数组中找到最大值max和最小值min
- 算出最大与最小之间有多少个数,范围range:max-min+1
- 开临时空间大小为range,每个元素初始化为0
- 待排序数组的元素减去最小值min即对应临时空间的下标,原数组出现的元素会在临时空间对应的位置计数
- 从小到大遍历临时空间数组,只要不为0,说明该位置是对应原数组有出现的元素,然后依次重新放入原数组,临时空间的下标加上最小值恢复到原数组的元素的值。
图示:

代码:
void CountSort(int* a, int n)
{//找最大值和最小值int max = a[0], min = a[0];for (int i = 0; i < n; i++){if (a[i] > max){max = a[i];}if (a[i] < min){min = a[i];}}//最大值与最小值的差int range = max - min + 1;//开空间,每个元素为0,后面要计数int* count = (int*)calloc(range, sizeof(int));if (count == nullptr){perror("calloc fail");exit(-1);}//给出现的元素计数for (int i = 0; i < n; i++){count[a[i] - min]++;}//从小到大重新放入数组,完成排序int j = 0;for (int i = 0; i < range; i++){while (count[i]--)//该位置有元素{a[j++] = i + min;//恢复原来的元素,依次放入数组}}free(count);
}
特性总结:
- 计数排序适用于数据较集中的场景
- 时间复杂度:O(N+range)
- 空间复杂度:O(range)
- 稳定
相关文章:

【排序篇2】选择排序、计数排序
目录 一、选择排序二、计数排序 一、选择排序 整体思想: 从数组中选出最小值和最大值放在起始位置,直到排序完成 具体步骤: 定义两个变量begin和end为下标,指向数组始末定义要找的最大值的下标为maxi,最小值的下标为…...
重生奇迹mu敏弓加点攻略
1. 选择正确的属性点分配 在重生奇迹mu游戏中敏弓的属性点分配非常重要。建议将主要属性点分配在敏捷和力量上这样可以提高敏弓的攻击力和闪避能力。适当加点在体力和魔力上可以提高敏弓的生存能力和技能释放次数。不要忘记适当加点在智力上可以提高敏弓的技能威力和命中率。 …...

用通俗易懂的方式讲解:一文讲透主流大语言模型的技术原理细节
大家好,今天的文章分享三个方面的内容: 1、比较 LLaMA、ChatGLM、Falcon 等大语言模型的细节:tokenizer、位置编码、Layer Normalization、激活函数等。 2、大语言模型的分布式训练技术:数据并行、张量模型并行、流水线并行、3D …...

通过IP地址识别风险用户
随着互联网的迅猛发展,网络安全成为企业和个人关注的焦点之一。识别和防范潜在的风险用户是维护网络安全的关键环节之一。IP数据云将探讨通过IP地址识别风险用户的方法和意义。 IP地址的基本概念:IP地址是互联网上设备的独特标识符,它分为IP…...

汇编和C语言转换
C语言和汇编语言之间有什么区别 C语言和汇编语言之间存在显著的区别,主要体现在以下几个方面: 抽象层次: 汇编语言:更接近硬件的低级语言,通常与特定的处理器或指令集紧密相关。它提供了对处理器指令的直接控制,允许程序员直接操作硬件资源,如寄存器、内存等。 C语言:…...
)
【IOS】惯性导航详解(包含角度、加速度、修正方式的api分析)
参考文献 iPhone的惯性导航,基于步态。https://www.docin.com/p-811792664.html Inertial Odometry on Handheld Smartphones: https://arxiv.org/pdf/1703.00154.pdf 惯性导航项目相关代码:https://github.com/topics/inertial-navigation-systems use…...
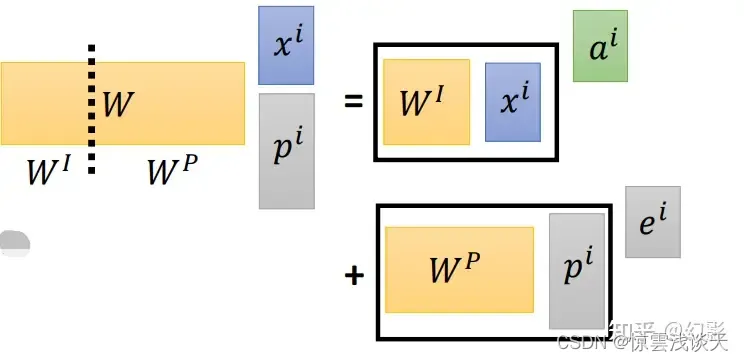
Self-Attention
前置知识:RNN,Attention机制 在一般任务的Encoder-Decoder框架中,输入Source和输出Target内容是不一样的,比如对于英-中机器翻译来说,Source是英文句子,Target是对应的翻译出的中文句子,Attent…...

网络协议与攻击模拟_04ICMP协议与ICMP重定向
ICMP协议是网络层协议, 利用ICMP协议可以实现网络中监听服务和拒绝服务,如 ICMP重定向的攻击。 一、ICMP基本概念 1、ICMP协议 ICMP是Internet控制报文协议,用于在IP主机、路由器之间传递控制消息,控制消息指网络通不通、主机是…...

pytest-mock 数据模拟
文章目录 mock 测试unittest.mockMock类MagicMock类patch装饰器create_autospec函数断言的方法 pytest-mock 使用 mock 测试 在单元测试时,有些数据需要依赖其他服务或者不好获取到,此时需要使用mock来模拟对应的函数、对象等。 mock模拟数据的python…...
单片机原理及应用:定时器/计数器综合应用
本文是《单片机原理及应用》专栏中的最后一篇文章,笔者以编译器的安装配置——51单片机简介——LED和数码管外设——开关和按键控制功能切换——外部中断系统——定时器与计数器为知识大纲,介绍了C语言编程控制51单片机的入门教程。作为收尾,…...

R语言【paleobioDB】——pbdb_intervals():通过参数选择,返回多个地层年代段的基本信息
Package paleobioDB version 0.7.0 paleobioDB 包在2020年已经停止更新,该包依赖PBDB v1 API。 可以选择在Index of /src/contrib/Archive/paleobioDB (r-project.org)下载安装包后,执行本地安装。 Usage pbdb_interval (id, ...) Arguments 参数【..…...
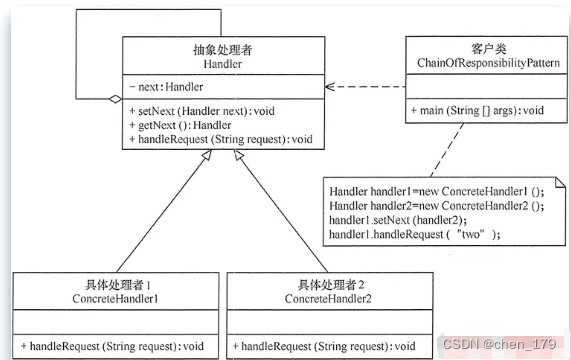
阅读笔记lv.1
阅读笔记 sql中各种 count结论不同存储引擎计算方式区别count() 类型 责任链模式常见场景例子(闯关游戏) sql中各种 count 结论 innodb count(*) ≈ count(1) > count(主键id) > count(普通索引列) > count(未加索引列)myisam 有专门字段记录…...

小鼠的滚动疲劳仪-转棒实验|ZL-200C小鼠转棒疲劳仪
转棒实验|ZL-200C小鼠转棒疲劳仪用于检测啮齿类动物的运动功能。通过测量动物在滚筒上行走的持续时间,来评定**神经系统*病或损坏以及药物对运动协调功能和疲劳的影响。 疲劳实验中,让小鼠在不停转动的棒上运动,肌肉会很快进入疲劳状态&#…...
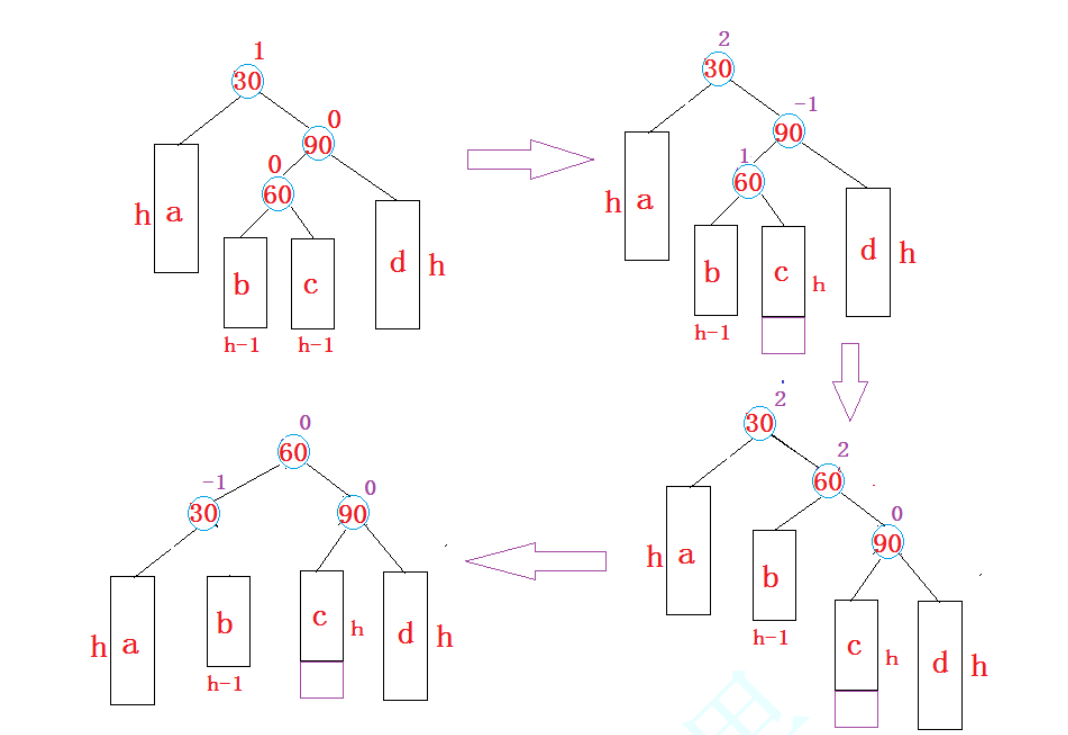
平衡搜索二叉树(AVL树)
目录 前言 一、AVL树的概念 二、AVL树的定义 三、AVL树的插入 四、AVL树的旋转 4.1、右单旋 4.2、左单旋 4.3、左右双旋 4.4、右左双旋 五、AVL树的验证 5.1、 验证其为二叉搜索树 5.2、 验证其为平衡树 六、AVL树的性能 前言 二叉搜索树虽可以缩短查找的效率&…...

2024年1月12日学习总结
学习目标 完成集中学习的readme 完成联邦学习的代码编写 边学习边总结 学习内容 Introduction to Early Stopping 1、Overfitting 过拟合是所有机器学习,深度学习中可能出现的一个比较严重的问题。具体表现就是:你的模型在训练集上处理的效果非常好&…...

PCL 使用克拉默法则进行四点定球(C++详细过程版)
目录 一、算法原理二、代码实现三、计算结果本文由CSDN点云侠原创,PCL 使用克拉默法则进行四点定球(C++详细过程版),爬虫自重。如果你不是在点云侠的博客中看到该文章,那么此处便是不要脸的爬虫与GPT生成的文章。 一、算法原理 已知空间内不共面的四个点,设其坐标为 A (…...

前端导致浏览器奔溃原因分析
内存泄漏 内存泄漏(Memory Leak)是指程序中已动态分配的堆内存由于某种原因程序未释放或无法释放,造成系统内存的浪费,导致程序运行速度减慢甚至系统崩溃等严重后果。(程序某个未使用的变量或者方法,长期占…...
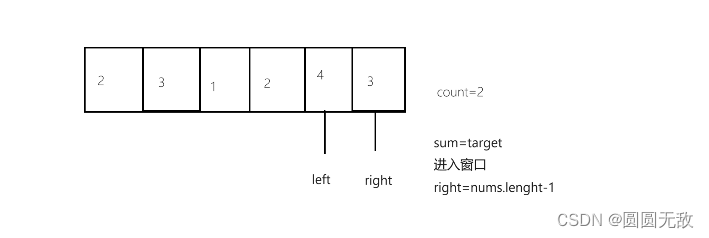
力扣:209.长度最小的子数组
1.题目分析: 给定一个含有 n 个正整数的数组和一个正整数 target 。 找出该数组中满足其总和大于等于 target 的长度最小的 连续子数组 [numsl, numsl1, ..., numsr-1, numsr] ,并返回其长度。如果不存在符合条件的子数组,返回 0 。 示例 …...

常见类型的yaml文件如何编写?--kind: Service
基本说明 在 Kubernetes 中,Service 是一种抽象的方式,用于定义一组 Pod 的访问方式和网络服务。Service 提供了一个稳定的网络端点(Endpoint),使得其他服务或外部用户可以通过 Service 来访问被管理的 Pod。 负载均…...

linux环境下安装postgresql
PostgreSQL: Linux downloads (Red Hat family)postgresql官网 PostgreSQL: Linux downloads (Red Hat family) 环境: centos7 postgresql14 选择版本 执行启动命令 配置远程连接文件 vi /var/lib/pqsql/14/data/postgresql.conf 这里将listen_addresses值由lo…...

多模态2025:技术路线“神仙打架”,视频生成冲上云霄
文|魏琳华 编|王一粟 一场大会,聚集了中国多模态大模型的“半壁江山”。 智源大会2025为期两天的论坛中,汇集了学界、创业公司和大厂等三方的热门选手,关于多模态的集中讨论达到了前所未有的热度。其中,…...

linux之kylin系统nginx的安装
一、nginx的作用 1.可做高性能的web服务器 直接处理静态资源(HTML/CSS/图片等),响应速度远超传统服务器类似apache支持高并发连接 2.反向代理服务器 隐藏后端服务器IP地址,提高安全性 3.负载均衡服务器 支持多种策略分发流量…...

汽车生产虚拟实训中的技能提升与生产优化
在制造业蓬勃发展的大背景下,虚拟教学实训宛如一颗璀璨的新星,正发挥着不可或缺且日益凸显的关键作用,源源不断地为企业的稳健前行与创新发展注入磅礴强大的动力。就以汽车制造企业这一极具代表性的行业主体为例,汽车生产线上各类…...

大语言模型如何处理长文本?常用文本分割技术详解
为什么需要文本分割? 引言:为什么需要文本分割?一、基础文本分割方法1. 按段落分割(Paragraph Splitting)2. 按句子分割(Sentence Splitting)二、高级文本分割策略3. 重叠分割(Sliding Window)4. 递归分割(Recursive Splitting)三、生产级工具推荐5. 使用LangChain的…...
指令的指南)
在Ubuntu中设置开机自动运行(sudo)指令的指南
在Ubuntu系统中,有时需要在系统启动时自动执行某些命令,特别是需要 sudo权限的指令。为了实现这一功能,可以使用多种方法,包括编写Systemd服务、配置 rc.local文件或使用 cron任务计划。本文将详细介绍这些方法,并提供…...

Module Federation 和 Native Federation 的比较
前言 Module Federation 是 Webpack 5 引入的微前端架构方案,允许不同独立构建的应用在运行时动态共享模块。 Native Federation 是 Angular 官方基于 Module Federation 理念实现的专为 Angular 优化的微前端方案。 概念解析 Module Federation (模块联邦) Modul…...

图表类系列各种样式PPT模版分享
图标图表系列PPT模版,柱状图PPT模版,线状图PPT模版,折线图PPT模版,饼状图PPT模版,雷达图PPT模版,树状图PPT模版 图表类系列各种样式PPT模版分享:图表系列PPT模板https://pan.quark.cn/s/20d40aa…...

3-11单元格区域边界定位(End属性)学习笔记
返回一个Range 对象,只读。该对象代表包含源区域的区域上端下端左端右端的最后一个单元格。等同于按键 End 向上键(End(xlUp))、End向下键(End(xlDown))、End向左键(End(xlToLeft)End向右键(End(xlToRight)) 注意:它移动的位置必须是相连的有内容的单元格…...

GC1808高性能24位立体声音频ADC芯片解析
1. 芯片概述 GC1808是一款24位立体声音频模数转换器(ADC),支持8kHz~96kHz采样率,集成Δ-Σ调制器、数字抗混叠滤波器和高通滤波器,适用于高保真音频采集场景。 2. 核心特性 高精度:24位分辨率,…...

微软PowerBI考试 PL300-在 Power BI 中清理、转换和加载数据
微软PowerBI考试 PL300-在 Power BI 中清理、转换和加载数据 Power Query 具有大量专门帮助您清理和准备数据以供分析的功能。 您将了解如何简化复杂模型、更改数据类型、重命名对象和透视数据。 您还将了解如何分析列,以便知晓哪些列包含有价值的数据,…...
