16. 蒙特卡洛强化学习基本概念与算法框架
文章目录
- 1. 是什么
- 2. 有何优点
- 3. 基本概念
- 3.1 立即回报
- 3.2 累积回报
- 3.3 状态值函数
- 3.4 行为值函数
- 3.4 回合(或完整轨迹,episode)
- 3.5 多个回合(或完整轨迹)的描述
- 4.MC强化学习问题的正式描述
- 5. 蒙特卡洛(MC)强化学习算法的基本框架
1. 是什么
蒙特卡洛强化学习(简称MC强化学习)是一种无模型强化学习算法,该算法无需知道马尔科夫决策环境模型,即不需要提前获得立即回报期望矩阵R(维度为(nS,nA))、状态转移概率数组P(维度为(nA,nS,nS)),而是通过与环境的反复交互,使用统计学方法,利用交互数据直接进行策略评估和策略优化,从而学到最优策略。
2. 有何优点
- 无需环境模型
- 易于编程、通用性强。
3. 基本概念
为了更好的描述MC方法,深入理解如下概念非常必要。
3.1 立即回报
- 在某状态 s t s_t st下,智能体执行某行为 a t a_t at后,获得的一次来自环境的即时奖励,例如,在格子世界中寻宝的实验中,智能体在距离宝藏较远的距离时,向右移动后,获得来自环境的即时奖励为-1,在智能体位于宝藏左边时,向右移动1格后,获奖来自环境的即时奖励为0.
- 立即回报是随机变量,为了反映它的特征,可以用立即回报期望来描述,符号为 R s a = E π ( R t + 1 ∣ s t = s , a t = a ) R_s^a=E_\pi(R_{t+1}|s_t=s,a_t=a) Rsa=Eπ(Rt+1∣st=s,at=a)
3.2 累积回报
G t = R t + 1 + γ R t + 2 + γ 2 R t + 3 + ⋯ = ∑ k = 1 T γ k − 1 R t + k G_t = R_{t+1}+\gamma R_{t+2}+\gamma^2 R_{t+3}+\cdots=\sum_{k=1}^{T}\gamma^{k-1}R_{t+k} Gt=Rt+1+γRt+2+γ2Rt+3+⋯=k=1∑Tγk−1Rt+k
- G t G_t Gt:从某个状态s开始,遵循某个策略时从状态s开始直到最后终止状态 s T s_T sT的带折扣的累积回报
- 由于 R t + k R_{t+k} Rt+k为随机变量,故 G t G_t Gt为随机变量;
3.3 状态值函数
- 为衡量状态s下遵循策略 π \pi π的价值,取状态值函数 V π ( s ) = E π ( G t ∣ s t = s ) V_\pi(s)=E_\pi(G_t|s_t=s) Vπ(s)=Eπ(Gt∣st=s)作为度量标准
- 为了从交互产生的统计数据中计算得到接近真实的状态值函数 V π ( s ) V_\pi(s) Vπ(s),可以取足够多回合的交互获得的 G t G_t Gt的样本的平均值
3.4 行为值函数
行为值函数是策略改进的依据,理论上,它可以通过状态值函数计算得到:
Q ( s , a ) = R s a + γ ∑ s ′ ∈ S P s s ′ a V ( s ′ ) Q(s,a) = R_s^a+\gamma\sum_{s'\in S}P_{ss'}^aV(s') Q(s,a)=Rsa+γs′∈S∑Pss′aV(s′)
然而,实际上,由于 R s a R_s^a Rsa与 P s s ′ a P_{ss'}^a Pss′a未知,因此,MC方法通常不会通过估计状态值函数 V ( s ) V(s) V(s),然后使用Q(s,a)进行策略改进。
MC方法是利用交互数据直接估计Q(s,a),然后再基于Q(s,a)进行策略改进的。
3.4 回合(或完整轨迹,episode)
- 由3.3可知,要获得1个 G t G_t Gt样本,可以让智能体从任意某初始状态出发,一直遵循某种策略 π \pi π与环境交互,直至状态转移到环境的终止状态 s T s_T sT才结束。
- 我们把从某状态 ∀ s ∈ S \forall s\in S ∀s∈S出发,到终止状态 s T s_T sT之间的完整状态、动作、立即回报的转换过程,称为1次完整的轨迹或1个回合,英文单词为Episode
3.5 多个回合(或完整轨迹)的描述
假设以任意起始状态开始的完整轨迹有多条条,则这多条完整轨迹可以表示为:
轨迹0: s 0 , 0 , a 0 , 0 , r 0 , 1 , s 0 , 1 , a 0 , 1 , r 0 , 2 , ⋯ , s 0 , L 0 , a 0 , L 0 , r 0 , L 0 + 1 , s T , a 0 , L 0 + 1 , r 0 , L 0 + 2 s_{0,0},a_{0,0},r_{0,1},s_{0,1},a_{0,1},r_{0,2},\cdots,s_{0,L_0},a_{0,L_0},r_{0,L_0+1},s_T,a_{0,L_0+1},r_{0,L_0+2} s0,0,a0,0,r0,1,s0,1,a0,1,r0,2,⋯,s0,L0,a0,L0,r0,L0+1,sT,a0,L0+1,r0,L0+2
轨迹1: s 1 , 0 , a 1 , 0 , r 1 , 1 , s 1 , 1 , a 1 , 1 , r 1 , 2 , ⋯ , s 1 , L 1 , a 1 , L 1 , r 1 , L 1 + 1 , s T , a 1 , L 1 + 1 , r 1 , L 1 + 2 s_{1,0},a_{1,0},r_{1,1},s_{1,1},a_{1,1},r_{1,2},\cdots,s_{1,L_1},a_{1,L_1},r_{1,L_1+1},s_T,a_{1,L_1+1},r_{1,L_1+2} s1,0,a1,0,r1,1,s1,1,a1,1,r1,2,⋯,s1,L1,a1,L1,r1,L1+1,sT,a1,L1+1,r1,L1+2
…
轨迹k: s k , 0 , a k , 0 , r k , 1 , s k , 1 , a k , 1 , r k , 2 , ⋯ , s k , L k , a k , L k , r k , L k + 1 , s T , a k , L k + 1 , r k , L k + 2 s_{k,0},a_{k,0},r_{k,1},s_{k,1},a_{k,1},r_{k,2},\cdots,s_{k,L_k},a_{k,L_k},r_{k,L_k+1},s_T,a_{k,L_k+1},r_{k,L_k+2} sk,0,ak,0,rk,1,sk,1,ak,1,rk,2,⋯,sk,Lk,ak,Lk,rk,Lk+1,sT,ak,Lk+1,rk,Lk+2
…
上述每条轨迹中的三元组 ( s k , m , a k , m , r k , m + 1 (s_{k,m},a_{k,m},r_{k,m+1} (sk,m,ak,m,rk,m+1表示轨迹k中,状态为 s k + m s_{k+m} sk+m,执行行为 a k + m a_{k+m} ak+m后获得的立即回报的采样值为 r k , m + 1 r_{k,m+1} rk,m+1, r k , L k + 1 r_{k,L_k+1} rk,Lk+1表示轨迹k时,智能体观测到的环境状态为终止状态的上一状态 s k , L k s_{k,L_k} sk,Lk下,执行动作 a k , L k a_{k,L_k} ak,Lk的立即回报采样。
可见,一条完整轨迹(回合或episode),必须满足:
- 最后一个状态值 s T s_T sT对应终止状态
- L k ≥ 0 L_k\ge 0 Lk≥0
4.MC强化学习问题的正式描述
已知:一个MDP(马尔科夫决策过程)环境的折扣系数 γ \gamma γ、环境与智能体的交互接口,利用这个接口,智能体可以获得从任意状态 s t ∈ S s_t \in S st∈S下,执行行为空间中的某个行为 a t ∈ A a_t \in A at∈A后,来自环境的即时回报 r t + 1 r_{t+1} rt+1和转移后的状态 s t + 1 s_{t+1} st+1、该新的状态是否为终止状态。
$$
求解:智能体如何利用环境的对外接口与环境交互,如何通过交互获得最优策略 π ∗ ( a ∣ s ) \pi^*(a|s) π∗(a∣s)?
5. 蒙特卡洛(MC)强化学习算法的基本框架
π ( a ∣ s ) = 初始策略 π s a m p l e ( a ∣ s ) = 蒙特卡诺采样策略 ( 可以和初始策略一样) Q ( s , a ) = 0 w h i l e T r u e : 依据 π s a m p l e 与环境交互生成完整轨迹 利用轨迹数据进行策略评估以更新 Q ( s , a ) 利用 Q ( s , a ) 进行策略控制以改进 π ( a ∣ s ) i f 满足结束条件 : b r e a k \begin{align*} &\pi(a|s)=初始策略\\ &\pi_{sample}(a|s)=蒙特卡诺采样策略(可以和初始策略一样)\\ &Q(s,a)=0\\ & while \quad True:\\ &\qquad 依据\pi_{sample}与环境交互生成完整轨迹\\ &\qquad 利用轨迹数据进行策略评估以更新Q(s,a)\\ &\qquad 利用Q(s,a)进行策略控制以改进\pi(a|s)\\ &\qquad if\quad 满足结束条件:\\ &\qquad \qquad break \end{align*} π(a∣s)=初始策略πsample(a∣s)=蒙特卡诺采样策略(可以和初始策略一样)Q(s,a)=0whileTrue:依据πsample与环境交互生成完整轨迹利用轨迹数据进行策略评估以更新Q(s,a)利用Q(s,a)进行策略控制以改进π(a∣s)if满足结束条件:break
可见,MC强化学习的关键在于策略评估与策略控制
相关文章:

16. 蒙特卡洛强化学习基本概念与算法框架
文章目录 1. 是什么2. 有何优点3. 基本概念3.1 立即回报3.2 累积回报3.3 状态值函数3.4 行为值函数3.4 回合(或完整轨迹,episode)3.5 多个回合(或完整轨迹)的描述 4.MC强化学习问题的正式描述5. 蒙特卡洛(M…...

QT中程序执行时间精准计算的三种方法及对比
一.QT程序在提升程序性能的调试中经常要计算一段程序的执行时间,下面介绍两种简单的实现方式,精确度都可以达到ms。 1.方式一 (1)代码: #include <QDateTime> qDebug() << "Current_date_and_tim…...

js下载方法分享*
JavaScript可以使用浏览器的API实现文件的下载,以下是一种常用的方法: 假设你已经有了一个文件 URL,你可以创建一个新的 a 标签,并将 href 属性设置为文件的 URL,然后模拟点击这个标签以开始下载。 function downloa…...

C# Stopwatch类_性能_时间计时器
文章只含部分属性方法等,有想了解全面的在下面链接中可以查看:.NET API browser Stopwatch 类 (System.Diagnostics) | Microsoft Learn 一、什么是Stopwatch Stopwatch:提供一组方法和属性,可以准确的测量运行时间。使用的时候需…...
鸿蒙原生应用再添新丁!天眼查 入局鸿蒙
鸿蒙原生应用再添新丁!天眼查 入局鸿蒙 来自 HarmonyOS 微博1月12日消息,#天眼查启动鸿蒙原生应用开发#作为累计用户数超6亿的头部商业信息查询平台,天眼查可以为商家企业,职场人士以及普通消费者等用户便捷和安全地提供查询海量…...

HarmonyOS4.0——ArkUI应用说明
一、ArkUI框架简介 ArkUI开发框架是方舟开发框架的简称,它是一套构建 HarmonyOS / OpenHarmony 应用界面的声明式UI开发框架,它使用极简的UI信息语法、丰富的UI组件以及实时界面语言工具,帮助开发者提升应用界面开发效率 30%,开发…...

基于模块自定义扩展字段的后端逻辑实现(二)
目录 一:创建表 二:代码逻辑 上一节我们详细讲解了自定义扩展字段的逻辑实现和表的设计,这一节我们以一个具体例子演示下,如何实现一个订单模块的自定义扩展数据。 一:创建表 订单主表: CREATE TABLE t_order ( …...

图像中部分RGB矩阵可视化
图像中部分RGB可视化 今天室友有个需求就是模仿下面这张图画个示意图: 大致就是把图像中的一小部分区域的RGB值可视化了一下。他居然不知道该怎么画,我寻思这不直接秒了。 import cv2 as cv import numpy as np import matplotlib.pyplot as pltclass …...

RPA财务机器人在厦门市海沧医院财务管理流程优化汇总的应用
目前国内外研究人员对于RPA机器人在财务管理流程优化领域中的应用研究层出不穷,但现有研究成果主要集中在财务业务单一领域,缺乏财务管理整体流程一体化管控的研究。RPA机器人的功能绝非单一的财务业务处理,无论从自身技术发展,或…...

聚焦老年生活与健康,“老有所依·情暖夕阳”元岗街社区微型养老博览会顺利开展
尊老敬老是中华民族的传统美德, 爱老助老是全社会的共同责任。 家有一老,如有一宝, 长者的生活情况是一个家庭的头等大事, 做好长者服务是街道和社区的重要工作。 2024年1月6日,由元岗街道党工委、元岗街道办事处、…...
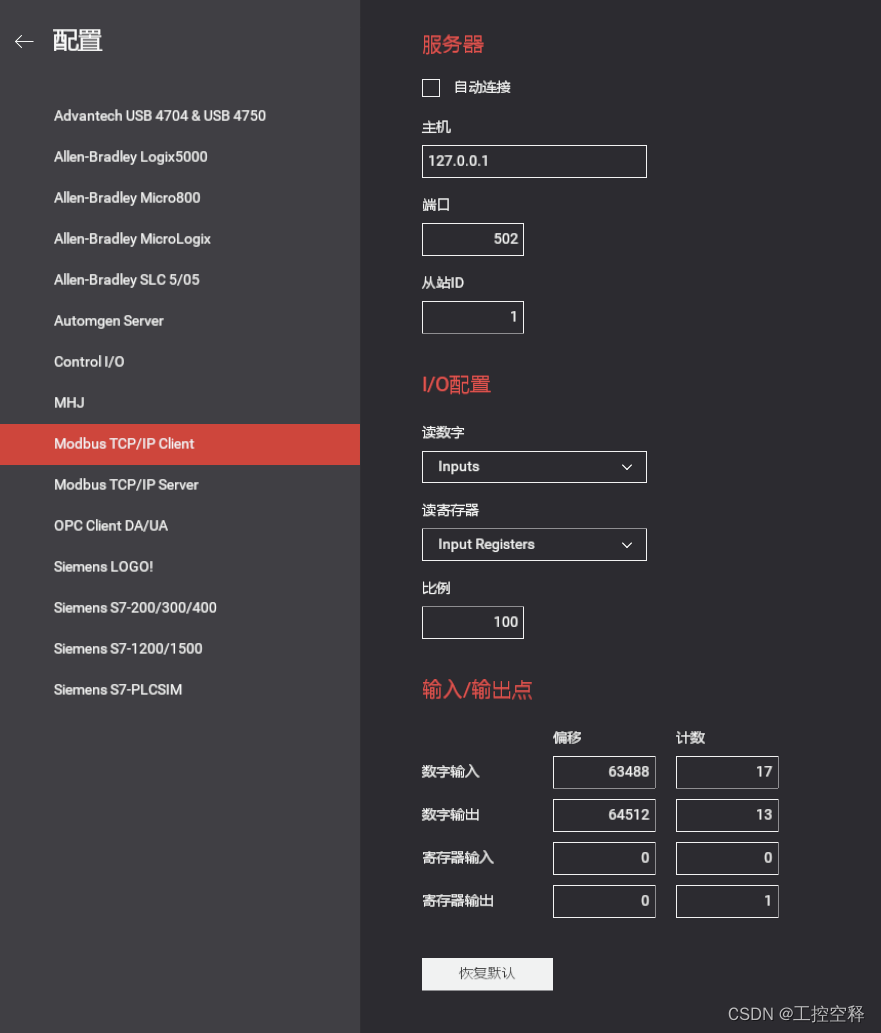
记录汇川:H5U与Factory IO测试12
主程序: 子程序: IO映射 子程序: 辅助出料 子程序: 自动程序 Factory IO配置: 实际动作如下: Factory IO测试12...
PingCAP 受邀参加 FICC 2023,获 Open100 世纪全球开源贡献奖
2023 年 12 月,2023 国际测试委员会智能计算与芯片联邦大会(FICC 2023)在海南三亚举办,中外院士和数十位领域专家莅临出席。 大会现场 ,开放源代码促进会创始人 Bruce Perens 颁发了 Open100 世纪全球开源贡献奖&…...

10-skywalking告警
https://github.com/apache/skywalking/blob/master/docs/en/setup/backend/backend-alarm.md 5.1:告警指标 ~$ vim /apps/apache-skywalking-apm-bin/config/oal/core.oal service_resp_time # 服务的响应时间 service_sla # 服务http请求成功率SLV,比…...
vue前端开发自学,插槽练习第二次,name属性的使用
vue前端开发自学,插槽练习第二次,name属性的使用!可以使用name属性,来自定义一个名字,这样,就可以在一个组件内同时出现多个插槽的内容了。在子组件内接收的时候,很简答,只需要在slot标签里面加上name“mz”࿱…...
AI副业拆解:人像卡通化,赋予你的形象全新生命力
大家好我是在看,记录普通人学习探索AI之路。 🔥让你的形象瞬间穿越二次元!🚀人像卡通化,捕捉你的独特魅力,让真实与梦幻在此刻交融。🎨 今天为大家介绍如何免费把人像卡通化--漫画风 https://w…...

宝塔面板安装MySQL8数据库
第一步:搜索mysql 第二步: 点击安装 我这里选择安装8版本 第三步:给宝塔配置mysql防火墙 第四步:修改数据库密码 第五步:想要使用navicat连接 需要修改root的权限 (1)使用secureCRT先登录mysql (2) 输入u…...
中科星图——Landsat9_C2_SR大气校正后的地表反射率数据
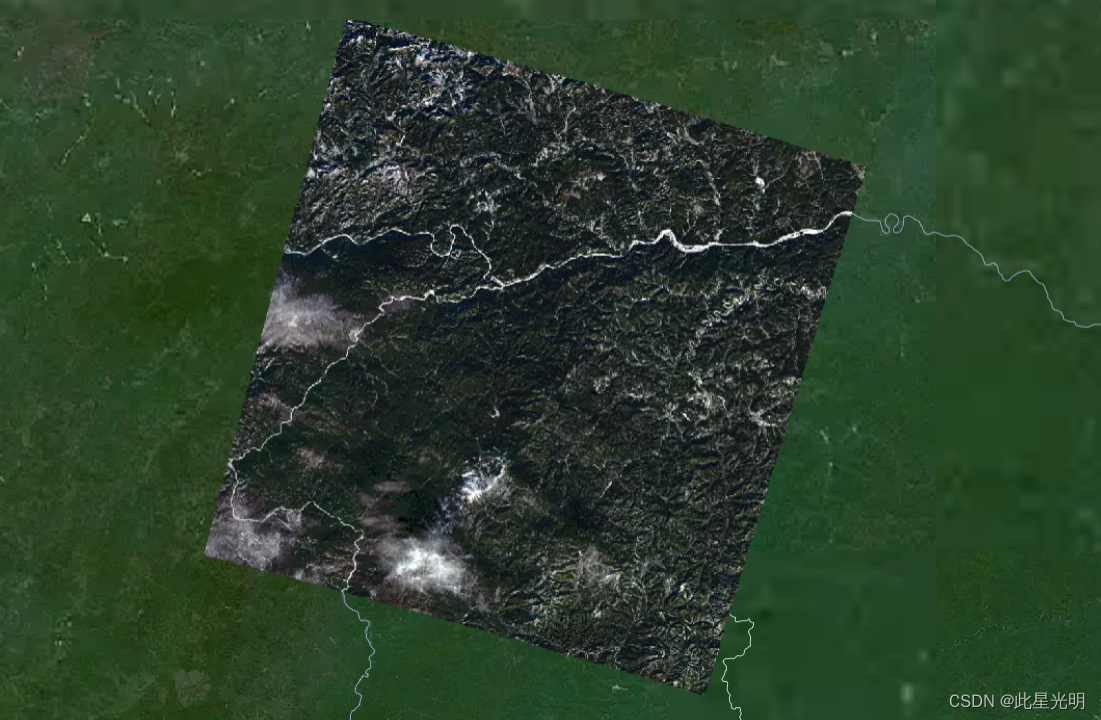
数据名称: Landsat9_C2_SR 数据来源: USGS 时空范围: 2022年1月-2023年3月 空间范围: 全国 数据简介: Landsat9_C2_SR数据集是经大气校正后的地表反射率数据,属于Collection2的二级数据产品&#…...
使用ros_arduino_bridge控制机器人底盘
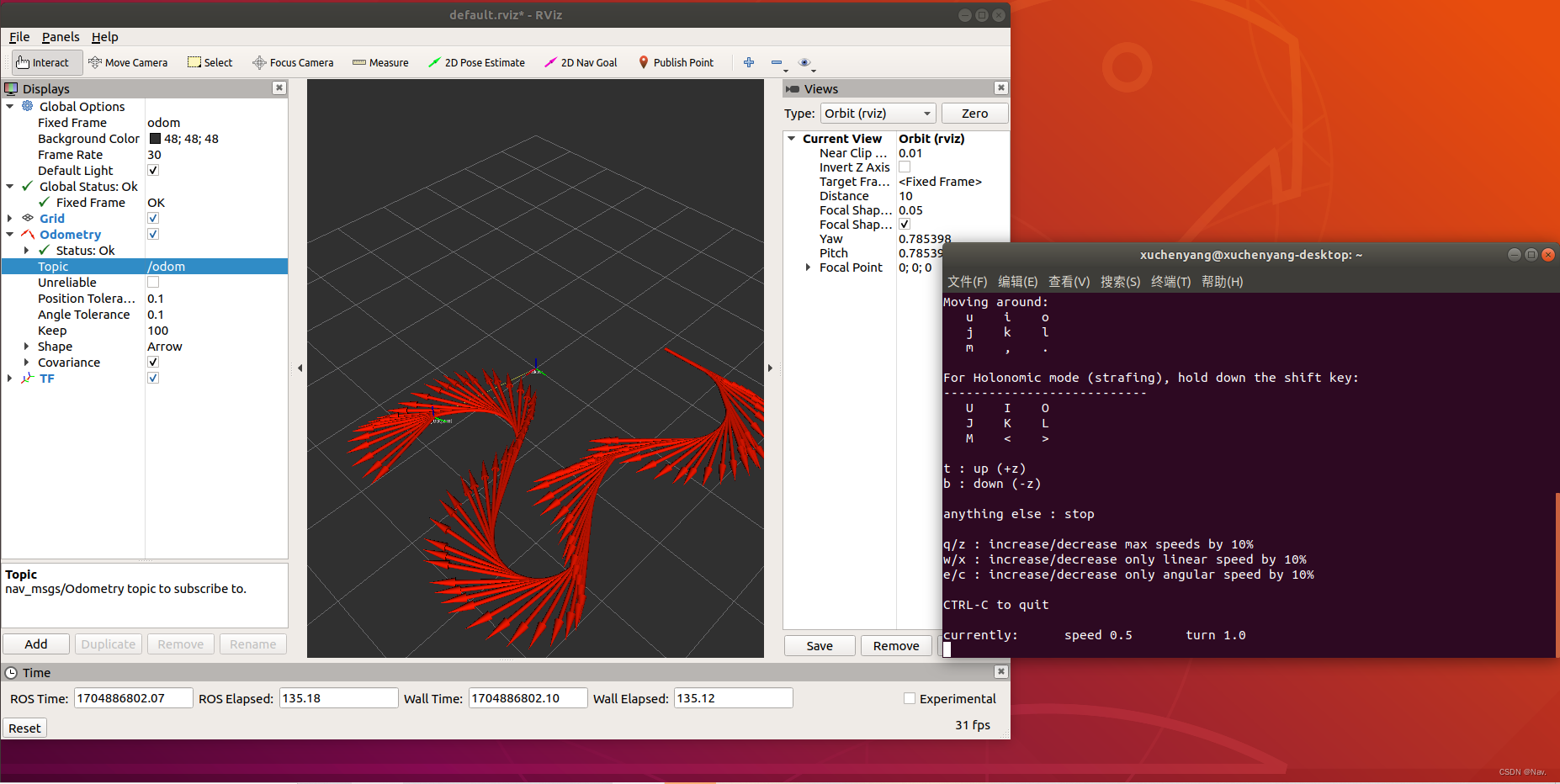
使用ros_arduino_bridge控制机器人底盘 搭建了ROS分布式环境后,将ros_arduino_bridge功能包上传至Jetson nano,就可以在PC端通过键盘控制小车的运动了。实现流程如下: 系统准备;下载程序;程序修改;分别启动PC与Jetson…...

Nacos下载与安装【windows】
🥚今日鸡汤🥚 我不知将去何方,但我已经在路上。 ——宫崎骏《千与千寻》 目录 🥞1.Nacosdi地址 🌭2.GitHub下载 🍿3.目录结构 🥓4.启动nacos 🧂5.客户端登陆 🧈…...
【随笔】遗传算法优化的BP神经网络(随笔,不是很详细)
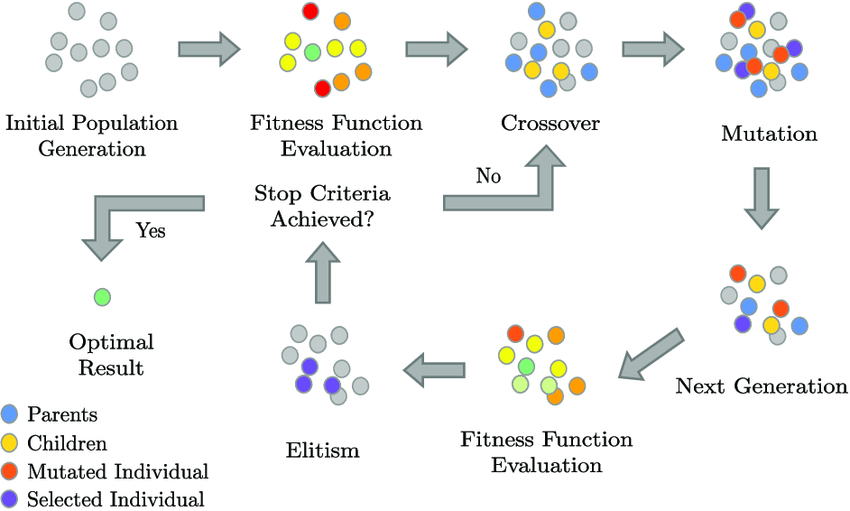
文章目录 一、算法思想1.1 BP神经网络1.2 遗传算法1.3 遗传算法优化的BP神经网络 二、代码解读2.1 数据预处理2.2 GABP2.3 部分函数说明 一、算法思想 1.1 BP神经网络 BP神经网络(Backpropagation Neural Network,反向传播神经网络)是一种监…...

未来机器人的大脑:如何用神经网络模拟器实现更智能的决策?
编辑:陈萍萍的公主一点人工一点智能 未来机器人的大脑:如何用神经网络模拟器实现更智能的决策?RWM通过双自回归机制有效解决了复合误差、部分可观测性和随机动力学等关键挑战,在不依赖领域特定归纳偏见的条件下实现了卓越的预测准…...

零门槛NAS搭建:WinNAS如何让普通电脑秒变私有云?
一、核心优势:专为Windows用户设计的极简NAS WinNAS由深圳耘想存储科技开发,是一款收费低廉但功能全面的Windows NAS工具,主打“无学习成本部署” 。与其他NAS软件相比,其优势在于: 无需硬件改造:将任意W…...

《Playwright:微软的自动化测试工具详解》
Playwright 简介:声明内容来自网络,将内容拼接整理出来的文档 Playwright 是微软开发的自动化测试工具,支持 Chrome、Firefox、Safari 等主流浏览器,提供多语言 API(Python、JavaScript、Java、.NET)。它的特点包括&a…...

关于nvm与node.js
1 安装nvm 安装过程中手动修改 nvm的安装路径, 以及修改 通过nvm安装node后正在使用的node的存放目录【这句话可能难以理解,但接着往下看你就了然了】 2 修改nvm中settings.txt文件配置 nvm安装成功后,通常在该文件中会出现以下配置&…...

【JVM】- 内存结构
引言 JVM:Java Virtual Machine 定义:Java虚拟机,Java二进制字节码的运行环境好处: 一次编写,到处运行自动内存管理,垃圾回收的功能数组下标越界检查(会抛异常,不会覆盖到其他代码…...

YSYX学习记录(八)
C语言,练习0: 先创建一个文件夹,我用的是物理机: 安装build-essential 练习1: 我注释掉了 #include <stdio.h> 出现下面错误 在你的文本编辑器中打开ex1文件,随机修改或删除一部分,之后…...

多模态商品数据接口:融合图像、语音与文字的下一代商品详情体验
一、多模态商品数据接口的技术架构 (一)多模态数据融合引擎 跨模态语义对齐 通过Transformer架构实现图像、语音、文字的语义关联。例如,当用户上传一张“蓝色连衣裙”的图片时,接口可自动提取图像中的颜色(RGB值&…...

vue3 字体颜色设置的多种方式
在Vue 3中设置字体颜色可以通过多种方式实现,这取决于你是想在组件内部直接设置,还是在CSS/SCSS/LESS等样式文件中定义。以下是几种常见的方法: 1. 内联样式 你可以直接在模板中使用style绑定来设置字体颜色。 <template><div :s…...

如何在看板中有效管理突发紧急任务
在看板中有效管理突发紧急任务需要:设立专门的紧急任务通道、重新调整任务优先级、保持适度的WIP(Work-in-Progress)弹性、优化任务处理流程、提高团队应对突发情况的敏捷性。其中,设立专门的紧急任务通道尤为重要,这能…...
:滤镜命令)
ffmpeg(四):滤镜命令
FFmpeg 的滤镜命令是用于音视频处理中的强大工具,可以完成剪裁、缩放、加水印、调色、合成、旋转、模糊、叠加字幕等复杂的操作。其核心语法格式一般如下: ffmpeg -i input.mp4 -vf "滤镜参数" output.mp4或者带音频滤镜: ffmpeg…...
