xtu-c语言考试复习-2
1223
确实写不出,数据远超过64位,难道用数组存吗,但是不好计算,想到的思路是取模,一边计算,一边取模,就不会超过数据范围,但是数学原理没懂,所以做不出来
看了下自己以前写的博客,确实是取模,以后积累经验,就是如果超过了数据范围,就直接用取模运算来控制这个范围
#include<stdio.h>
#include<stdbool.h>int main()
{int t;scanf("%d",&t);while(t--){int m;scanf("%d",&m);int k=1;int cnt=1;bool flag=false;for(int i=1;i<1000000;i++){k%=m;if(k==0) {printf("%d\n",cnt);flag=true;break;}k=k*10+1;cnt++;}if(!flag) puts("0");}return 0;
}
看自己博客又敲了一遍,WA了一次,因为我把循环的上界设置为了输入的数字,但是是不可取的,好吧,又试了一下,把上界设成输入的数字,取到等于号就可以过了
1308
样例能过,但是WA,实在想不通
#include<stdio.h>int main()
{int t;scanf("%d",&t);while(t--){int n;scanf("%d",&n);int cnt1=0,cnt2=0;while(n!=1){int temp=n%2;int m=n-temp;m/=2;cnt1++;cnt2+=m;n=n-m;}printf("%d %d\n",cnt1,cnt2);}return 0;
}
确实是自己没有考虑到位,应该是没有考虑需要比赛的人数是偶数的情况,先补上一份按照之前博客写的代码,再看下能不能把上面的代码改对
#include<stdio.h>int main()
{int t;scanf("%d",&t);while(t--){int n;scanf("%d",&n);int cnt1=0,cnt2=0;int m=0;while(n>1){m=1;while(m<n) m*=2;if(m!=n) m/=2;cnt1++;cnt2+=m/2;n=n-m/2;}//printf("%d\n",m);printf("%d %d\n",cnt1,cnt2);}return 0;
}
改了一下还是改不出来,想不明白
相关文章:

xtu-c语言考试复习-2
1223 确实写不出,数据远超过64位,难道用数组存吗,但是不好计算,想到的思路是取模,一边计算,一边取模,就不会超过数据范围,但是数学原理没懂,所以做不出来 看了下自己以…...

MySQL决战:MySQL数据导入导出
目录 前言 一.navact数据导入导出(第三方工具) 1.导入数据 2.数据导出 二. mysqldump命令导入导出数据 1.mysqldump介绍 2.数据导出 3.数据导入 三.load data file进行数据导入导出(只限于单表) 1.数据导出 增加导出权…...
Unity基础篇 【全面总结 | 持续更新】)
Unity 面试篇|(二)Unity基础篇 【全面总结 | 持续更新】
目录 1.Unity3d脚本从唤醒到销毁有着一套比较完整的生命周期,列出系统自带的几个重要的方法。2.Unity3D中的碰撞器和触发器的区别?3.物体发生碰撞的必要条件?4.简述Unity3D支持的作为脚本的语言的名称?5. .Net与Mono的关系&#x…...

TIDB的忘了root用户密码和数据库密码解决办法
方法一: 1、修改配置文件重启tidb,无密码登录修改root密码 找到配置文件 tidb.toml ,在[security] 作用域下增加如下配置: [security] skip-grant-tabletrue 重启tidb: sh run_tidb.sh 2、重启后,就可以无密…...
QT5基本对话框)
QT基础篇(4)QT5基本对话框
1.标准文件对话框类 在QT5中,可以使用QFileDialog类来创建标准文件对话框。QFileDialog类提供了一些方法和属性,用于选择文件和目录。 常用的方法和属性如下: getOpenFileName():打开文件对话框,选择一个文件。 get…...
Springboot项目Nacos做配置中心
Springboot项目Nacos做配置中心 说明安装2.Springboot整合使用Nacos3.问题处理 说明 文档参考 Nacos Spring Boot 安装 查看nacos镜像 docker search nacos 下载镜像 docker pull nacos/nacos-server启动naocs镜像 docker run --env MODEstandalone --name nacos -d -p 8…...
多用户身份认证)
SpringSecurity入门demo(三)多用户身份认证
WebSecurityConfigurerAdapter配置文件在 configure(AuthenticationManagerBuilder auth) 方法中完成身份认证。前面的demo都只有一个用户,security中使用UserDetailsService做为用户数据源 ,所以可以实现UserDetailsService 接口来自定义用户。实现方…...
【设计模式-02】Strategy策略模式及应用场景
一、参考资料 Java 官方文档 Overview (Java SE 18 & JDK 18)module indexhttps://docs.oracle.com/en/java/javase/18/docs/api/index.html Java中使用到的策略模式 Comparator、comparable Comparator (Java SE 18 & JDK 18)declaration: module: java.base, pa…...

ssh远程登陆
一、ssh远程登陆的概念 SSH(Secure Shell)是一种安全通道协议,主要用来实现字符界面的远程登录、远程 复制等功能。SSH 协议对通信双方的数据传输进行了加密处理,其中包括用户登录时输入的用户口令,SSH 为建立在应用层…...

go如何终止多个for select循环嵌套
空山新雨后,天气晚来秋。 目录 分类说明 总结 分类说明 for select循环嵌套,如何终止?上代码: stop : make(chan struct{})go func() {for i : 1; i < 3; i {fmt.Println("writed ", i)time.Sleep(time.Second * …...
nginx(1.13.7)首次安装出现:【make: *** 没有规则可以创建“default”需要的目标“build” 问题】解决措施
目录 前言: 一.龙蜥(Anolis)操作系统上安装GCC 1.安装gcc 2.检验安装 二.安装出现 make: *** 没有规则可以创建“default”需要的目标“build” 问题 1.解压安装nginx 2.安装出现问题展示 3.解决措施 4.重新编译进行安装 5…...
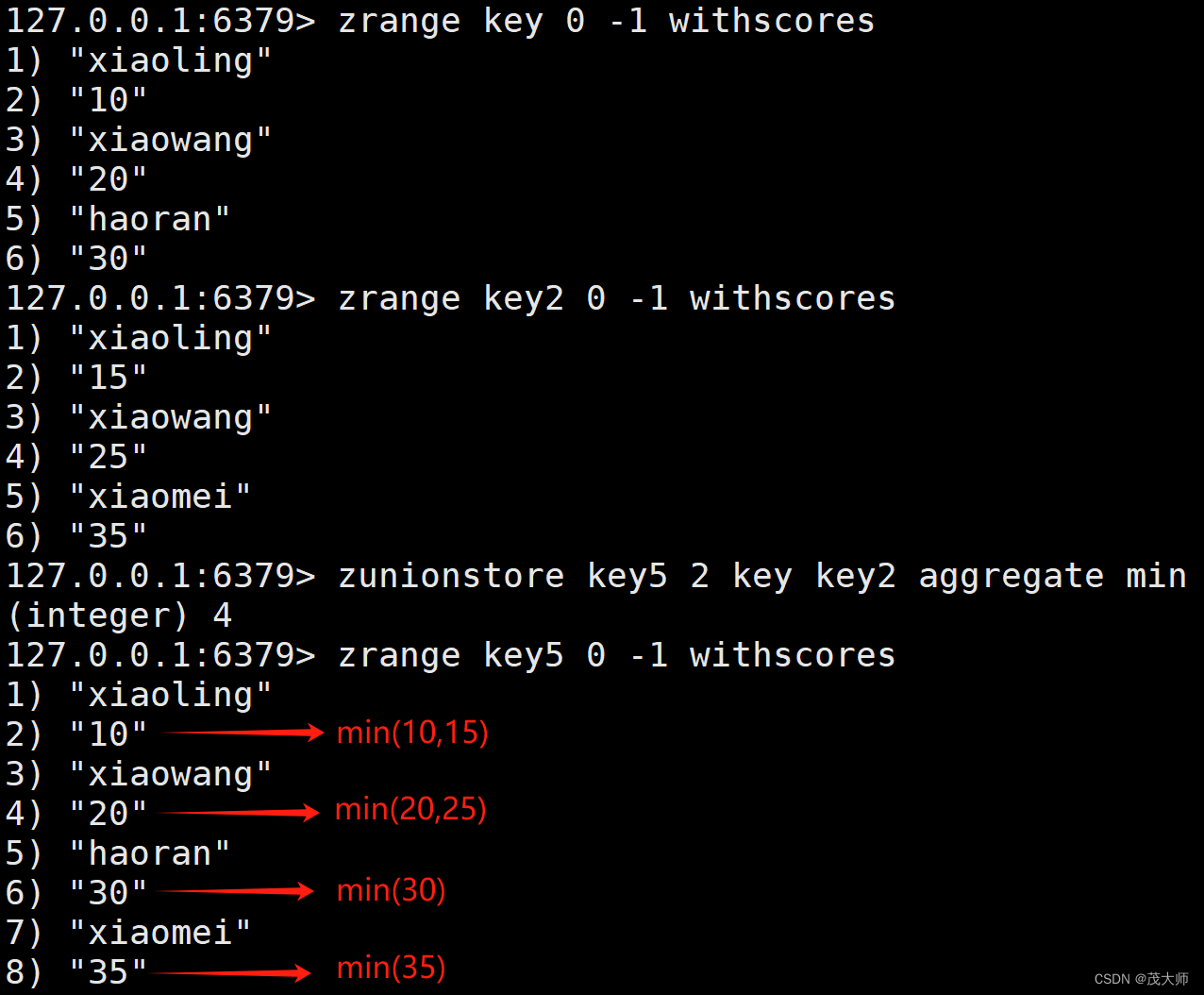
2024.1.8 关于 Redis 数据类型 Zset 集合命令、编码方式、应用场景
目录 引言 Zset 集合命令 ZINTERSTORE ZUNIONSTORE Zset 编码方式 Zset 应用场景 排行榜系统 引言 在 Redis 中集合间操作无非就是 交集、并集、差集 Set 类型与之相对应的操作命令为 sinter、sunion、sdiff 注意: 从 Redis 6.2 版本开始,Zset 命…...
ffmpeg[学习(四)](代码实现) 实现音频数据解码并且用SDL播放
0、作者杂谈 CSDN大多数都是落后的,要么是到处复制粘贴的,对于初学者我来说困惑了很久,大多数CSDN文章都是使用旧的API ,已经被否决了,于是我读一些官方文档,和一些开源项目音视频的输出过程,写…...

C++ 字符串哈希 || 字符串前缀哈希法
字符串Hash就是构造一个数字使之唯一代表一个字符串。但是为了将映射关系进行一一对应,也就是,一个字符串对应一个数字,那么一个数字也对应一个字符串。 用字符串Hash的目的是,我们如果要比较一个字符串,我们不用直接比…...

【java】项目部署liunx服务器的简单步骤
在Linux服务器上部署Java项目通常涉及到一系列步骤,下面是一个基本的部署流程,具体步骤可能会根据项目和服务器环境的不同而有所调整: 1. 准备工作: 1.1 安装Java环境: 在Linux服务器上安装Java运行环境,…...
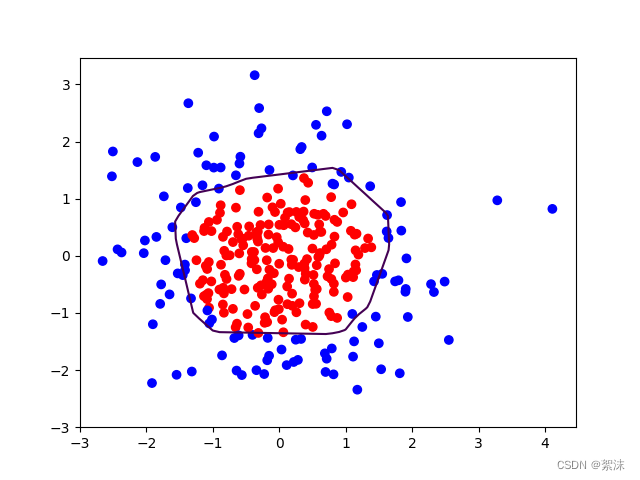
深度学习笔记(五)——网络优化(1):学习率自调整、激活函数、损失函数、正则化
文中程序以Tensorflow-2.6.0为例 部分概念包含笔者个人理解,如有遗漏或错误,欢迎评论或私信指正。 截图和程序部分引用自北京大学机器学习公开课 通过学习已经掌握了主要的基础函数之后具备了搭建一个网络并使其正常运行的能力,那下一步我们还…...

鸿蒙开发现在就业前景怎样?
随着科技的不断进步,鸿蒙系统逐渐崭露头角,成为智能设备领域的一颗新星。作为华为自主研发的操作系统,鸿蒙系统拥有着广阔的市场前景和就业机会。那么,鸿蒙开发的就业前景究竟怎样呢? 一、市场需求持续增长 随着鸿蒙…...
试用统信服务器操作系统UOS 20
作者:田逸(formyz) 试用统信Linux操作系统UOS,想了解一下用已有的Linux经验能否轻松驾驭它。以便在某些场景下,可以多一种选择。本次试验在Proxmox VE 8(以下简称PVE 8)平台下进行,采…...
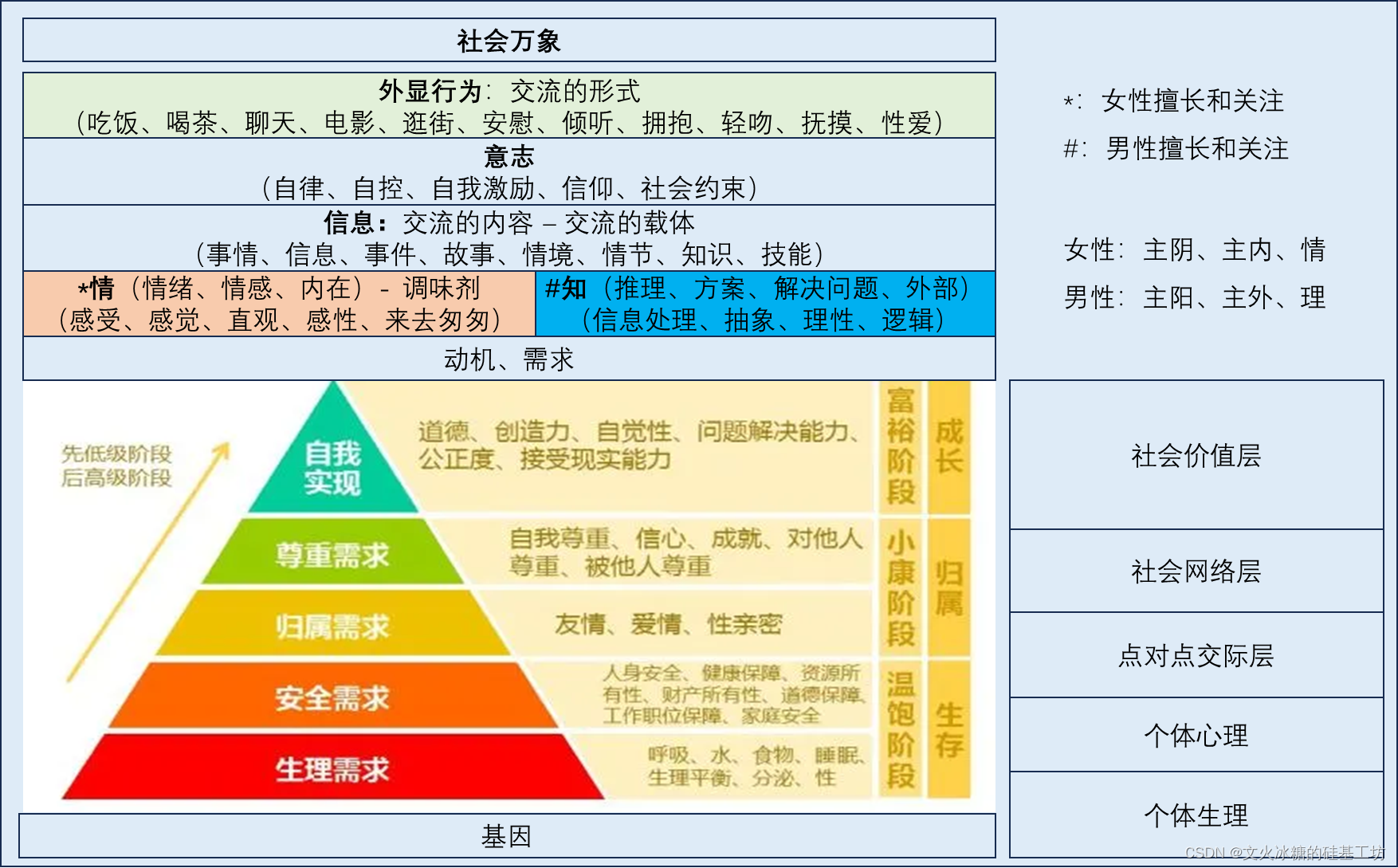
[情商-11]:人际交流的心理架构与需求层次模型
目录 前言: 一、心理架构 1.1 个体生理层 1.2 个体心理层 1.3 点对点人际交流层 1.4 社会网络层 1.5 社会价值层 二、人的需求层次模型 2.1 需求(欲望)层次模型 2.2 基因与人需求之间的关系 2.3 个体生理需求 2.4 个体的心理需求…...

【.NET Core】Lazy<T> 实现延迟加载详解
【.NET Core】Lazy 实现延迟加载详解 文章目录 【.NET Core】Lazy<T> 实现延迟加载详解一、概述二、Lazy<T>是什么三、Lazy基本用法3.1 构造时使用默认的初始化方式3.2 构造时使用指定的委托初始化 四、Lazy.Value使用五、Lazy扩展用法5.1 实现延迟属性5.2 Lazy实现…...

Lombok 的 @Data 注解失效,未生成 getter/setter 方法引发的HTTP 406 错误
HTTP 状态码 406 (Not Acceptable) 和 500 (Internal Server Error) 是两类完全不同的错误,它们的含义、原因和解决方法都有显著区别。以下是详细对比: 1. HTTP 406 (Not Acceptable) 含义: 客户端请求的内容类型与服务器支持的内容类型不匹…...

解决Ubuntu22.04 VMware失败的问题 ubuntu入门之二十八
现象1 打开VMware失败 Ubuntu升级之后打开VMware上报需要安装vmmon和vmnet,点击确认后如下提示 最终上报fail 解决方法 内核升级导致,需要在新内核下重新下载编译安装 查看版本 $ vmware -v VMware Workstation 17.5.1 build-23298084$ lsb_release…...

连锁超市冷库节能解决方案:如何实现超市降本增效
在连锁超市冷库运营中,高能耗、设备损耗快、人工管理低效等问题长期困扰企业。御控冷库节能解决方案通过智能控制化霜、按需化霜、实时监控、故障诊断、自动预警、远程控制开关六大核心技术,实现年省电费15%-60%,且不改动原有装备、安装快捷、…...

【CSS position 属性】static、relative、fixed、absolute 、sticky详细介绍,多层嵌套定位示例
文章目录 ★ position 的五种类型及基本用法 ★ 一、position 属性概述 二、position 的五种类型详解(初学者版) 1. static(默认值) 2. relative(相对定位) 3. absolute(绝对定位) 4. fixed(固定定位) 5. sticky(粘性定位) 三、定位元素的层级关系(z-i…...

【OSG学习笔记】Day 16: 骨骼动画与蒙皮(osgAnimation)
骨骼动画基础 骨骼动画是 3D 计算机图形中常用的技术,它通过以下两个主要组件实现角色动画。 骨骼系统 (Skeleton):由层级结构的骨头组成,类似于人体骨骼蒙皮 (Mesh Skinning):将模型网格顶点绑定到骨骼上,使骨骼移动…...
)
【HarmonyOS 5 开发速记】如何获取用户信息(头像/昵称/手机号)
1.获取 authorizationCode: 2.利用 authorizationCode 获取 accessToken:文档中心 3.获取手机:文档中心 4.获取昵称头像:文档中心 首先创建 request 若要获取手机号,scope必填 phone,permissions 必填 …...

音视频——I2S 协议详解
I2S 协议详解 I2S (Inter-IC Sound) 协议是一种串行总线协议,专门用于在数字音频设备之间传输数字音频数据。它由飞利浦(Philips)公司开发,以其简单、高效和广泛的兼容性而闻名。 1. 信号线 I2S 协议通常使用三根或四根信号线&a…...

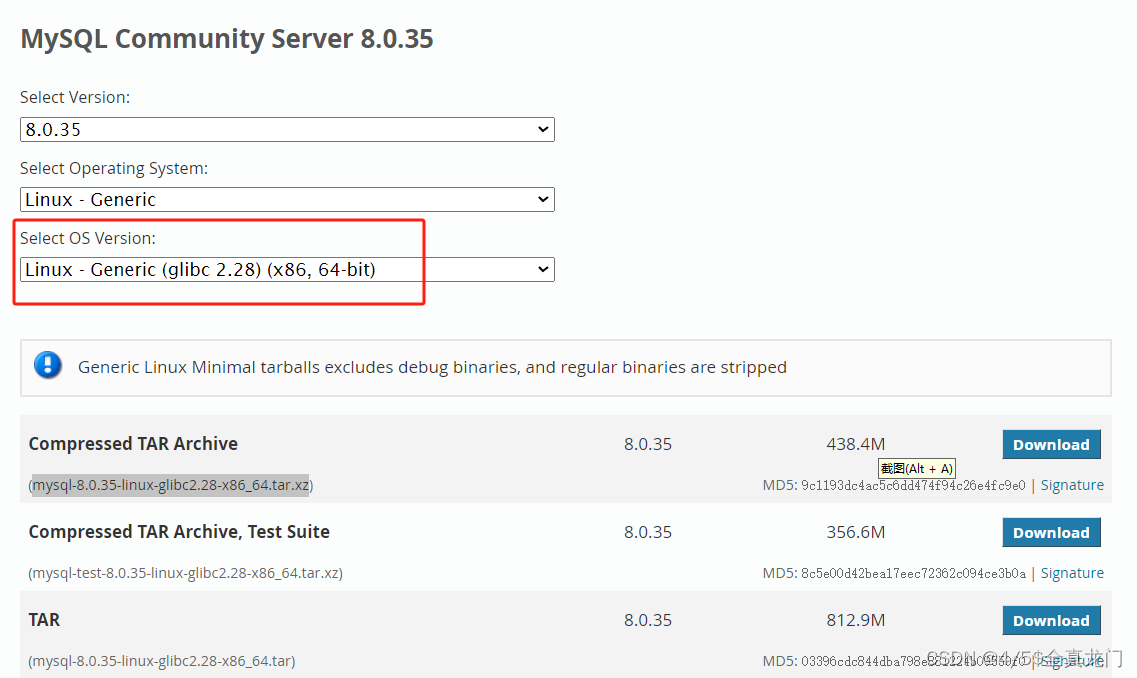
MySQL 知识小结(一)
一、my.cnf配置详解 我们知道安装MySQL有两种方式来安装咱们的MySQL数据库,分别是二进制安装编译数据库或者使用三方yum来进行安装,第三方yum的安装相对于二进制压缩包的安装更快捷,但是文件存放起来数据比较冗余,用二进制能够更好管理咱们M…...

虚拟电厂发展三大趋势:市场化、技术主导、车网互联
市场化:从政策驱动到多元盈利 政策全面赋能 2025年4月,国家发改委、能源局发布《关于加快推进虚拟电厂发展的指导意见》,首次明确虚拟电厂为“独立市场主体”,提出硬性目标:2027年全国调节能力≥2000万千瓦࿰…...

RabbitMQ入门4.1.0版本(基于java、SpringBoot操作)
RabbitMQ 一、RabbitMQ概述 RabbitMQ RabbitMQ最初由LShift和CohesiveFT于2007年开发,后来由Pivotal Software Inc.(现为VMware子公司)接管。RabbitMQ 是一个开源的消息代理和队列服务器,用 Erlang 语言编写。广泛应用于各种分布…...
