2024.1.8 关于 Redis 数据类型 Zset 集合命令、编码方式、应用场景
目录
引言
Zset 集合命令
ZINTERSTORE
ZUNIONSTORE
Zset 编码方式
Zset 应用场景
排行榜系统
引言
- 在 Redis 中集合间操作无非就是 交集、并集、差集
- Set 类型与之相对应的操作命令为 sinter、sunion、sdiff
注意:
- 从 Redis 6.2 版本开始,Zset 命令才开始支持 zinter、zunion、zdiff 这几个命令
- 但是此处我们使用的是 Redis 5 版本,所以下文不涉及介绍这三个命令
Zset 集合命令
ZINTERSTORE
- 用于求出给定有序集合中元素的交集,并将其保存进目标有序集合中
- 合并过程中以元素为单位进行合并,元素对应的分数按照不同的聚合方式和权重得到新的分数
语法:
zinterstore destination numkeys key [key ...] [WEIGHTS weight [weight ...]] [AGGREGATE <sum | min | max>]
- destination:表示要把结果存储到哪个 key 对应的 zset 中
- numkeys:描述了后续有几个 key 参与交集运算,因此该变量需为整型
- weight:可理解为 权重,此处指定的权重,相当于一个系数,会乘以当前的分数
- aggregate:指定 当前给定的有序集合 应采用哪种聚合方式来得出新的分数
注意:
- 前面介绍的命令也是支持多个 key 的,如mget、mset 等
- 但这些命令却不涉及到类似于此处的设定,即需手动指出 key 的个数
官方文档解释:
- 主要是为了避免 zinterstore 命令的 选项 和 keys 弄混淆
- 即通过 numkeys 描述出 key 的个数后,便可明确知道后面的 "选项" 是从哪里开始的
总结:
- 正因为 mget、mset 等命令,在指定 keys 后无复杂的选项
- 所以无需采用 numkeys 来手动指出 key 的个数,以便知道 key 和 选项 之间的分界处
时间复杂度:
- O(N) + O(M * logM)
- N 为 所有输入命令中总的 有序集合 元素个数
- M 为 结果集 的元素个数
实例理解
- 此处我们可以指定 权重
- 我们还可以指定 聚合方式
ZUNIONSTORE
- 用于求出给定有序集合的并集,并将其保存到目标有序集合中
- 合并过程中以元素为单位进行合并,元素对应的分数按照不同的聚合方式和权重得到新的分数
语法:
zunionstore destination numkeys key [key ...] [WEIGHTS weight [weight ...]] [AGGREGATE <sum | min | max>]
- zunionstore 和 zinterstore 命令的用法大致相同
时间复杂度:
- O(N) + O(M * logM)
- N 为 所有输入命令中总的 有序集合 元素个数
- M 为 结果集 的元素个数
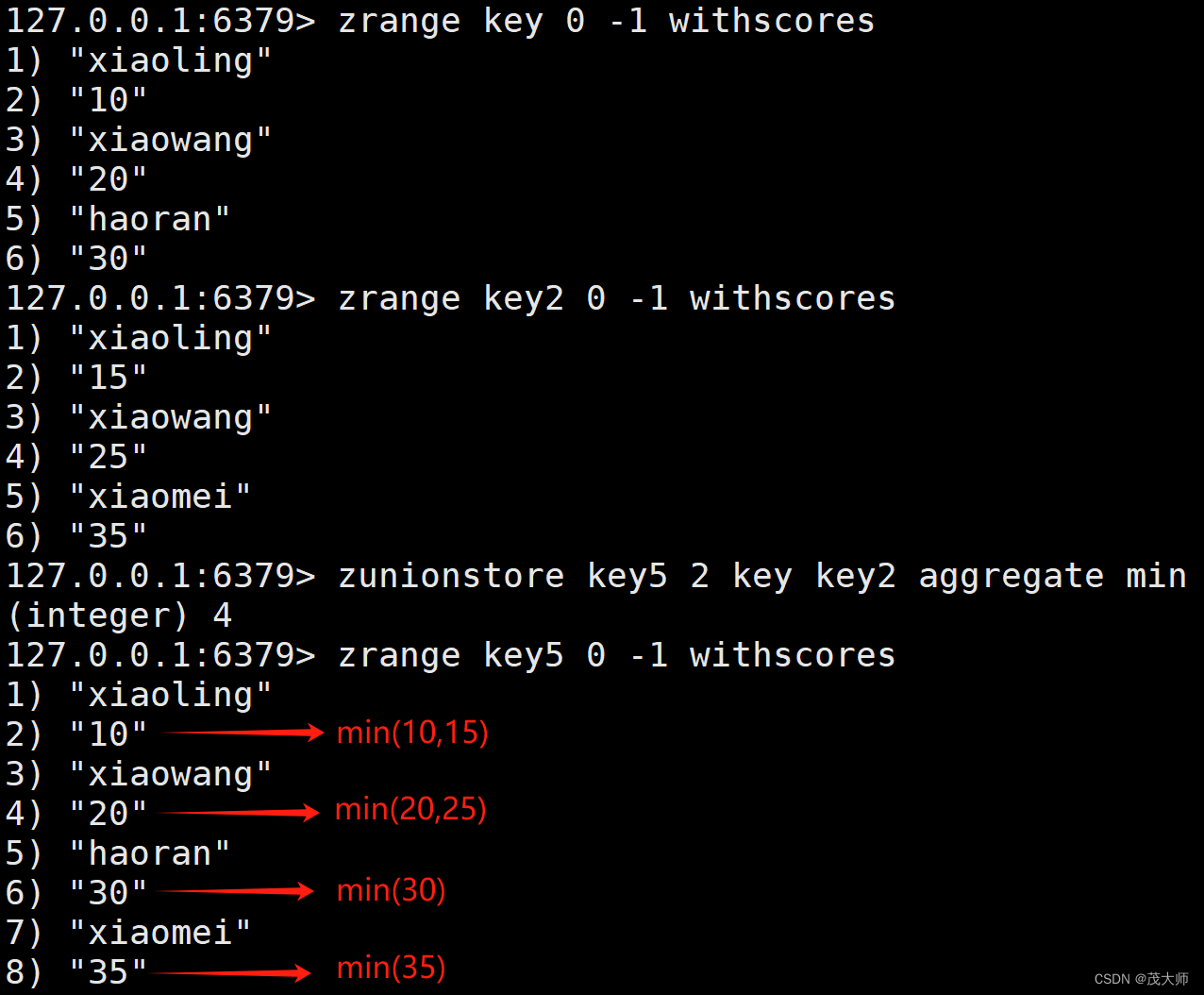
实例理解
- 此处我们可以指定 权重
- 我们还可以指定 聚合方式
Zset 编码方式
- 有序集合的内部编码有 两种
- ziplist(压缩列表)
- skiplist(跳表)
注意点一:
- 如果有序集合中的元素个数较少,或者单个元素体积较小时
- 使用 ziplist 来存储,以达到 节省空间 的效果
注意点二:
- 如果有序集合中的元素个数较多,或者单个元素体积非常大时
- 使用 skiplist 来存储
两个配置项
- zset-max-ziplist-entries:(单位为元素个数)
- zset-max-ziplist-value:(单位为字节)
- 当有序集合的元素个数小于 1号配置项,当每个元素的值都小于 2号配置项时
- Redis 会使用 ziplist 来作为有序集合的内部编码
关于跳表
- 简单来说,跳表是一个 复杂链表,其查询元素的时间复杂度为 O(logN)
- 相比于树形结构,更适合按照范围获取元素(B+ 树)
Zset 应用场景
排行榜系统
- 微博热搜、游戏天梯排行、成绩排行等
关键要点:
- 用来排行的分数为实时变化的
- 虽然是实时变化的,却也能够高效的更新排行
重点理解:
- 有序集合(zset) 能很好的满足上述需求和关键要点
实例理解
- 比如游戏天梯排行
- 只需要将 玩家信息和该玩家所对应的分数给放到有序集合中即可
- 从而便能 自动就形成一个排行榜
- 我们也能 随时按照排行(下标)、按照分数 来进行范围查询
- 随着分数发生改变,也可以比较方便的使用 zincrby 命令来修改分数,且排行榜顺序也能自动进行调整,该操作的时间复杂度为 O(logN)
问题:
- 游戏玩家这么多,此时都用这个 zset 来存,内存能否存下?
举例:
- 假设此时我们有 1亿 个玩家
- 约定 userId 4个字节,score 8个字节,即一个玩家需要 12 个字节来表示
- 12亿 字节 ——> 1.2 GB,对于当今计算机来说,绰绰有余!
实例理解二
- 相较于游戏排行榜,其排序依据很容易确定,仅需根据玩家积分即可
- 微博的排行榜,其排序依据评估起来更为复杂,因为 微博热度是一个综合数值!
- 其参考方面包含 浏览量、点赞量、转发量、评论量等
- 上述各方面具有不同 权重 weight,进而计算得到综合数值(热度)
重点理解
- 此时可以借助 zinterstore / zunionstore 命令,按照加权方式进行处理
- 可以把上述每个维度的数值均放到一个有序集合中
- member 为 微博的id,score 为各自维度的数值
- 通过 zinterstore / zunionstore 命令将上述有序集合按照约定好的权重,进行集合间运算即可
- 最终得到结果集合,其分数便为热度,且 排行榜也顺带着出来了!
总结:
- 上述应用场景,Redis 中的 zset 是一个选择,但不是说非得用 Reids 中的 zset 不可
- 有些场景下确实可以使用到有序集合,但又不方便使用 Redis 时,可以考虑使用其他方式的有序集合
相关文章:
2024.1.8 关于 Redis 数据类型 Zset 集合命令、编码方式、应用场景
目录 引言 Zset 集合命令 ZINTERSTORE ZUNIONSTORE Zset 编码方式 Zset 应用场景 排行榜系统 引言 在 Redis 中集合间操作无非就是 交集、并集、差集 Set 类型与之相对应的操作命令为 sinter、sunion、sdiff 注意: 从 Redis 6.2 版本开始,Zset 命…...
ffmpeg[学习(四)](代码实现) 实现音频数据解码并且用SDL播放
0、作者杂谈 CSDN大多数都是落后的,要么是到处复制粘贴的,对于初学者我来说困惑了很久,大多数CSDN文章都是使用旧的API ,已经被否决了,于是我读一些官方文档,和一些开源项目音视频的输出过程,写…...

C++ 字符串哈希 || 字符串前缀哈希法
字符串Hash就是构造一个数字使之唯一代表一个字符串。但是为了将映射关系进行一一对应,也就是,一个字符串对应一个数字,那么一个数字也对应一个字符串。 用字符串Hash的目的是,我们如果要比较一个字符串,我们不用直接比…...

【java】项目部署liunx服务器的简单步骤
在Linux服务器上部署Java项目通常涉及到一系列步骤,下面是一个基本的部署流程,具体步骤可能会根据项目和服务器环境的不同而有所调整: 1. 准备工作: 1.1 安装Java环境: 在Linux服务器上安装Java运行环境,…...
深度学习笔记(五)——网络优化(1):学习率自调整、激活函数、损失函数、正则化
文中程序以Tensorflow-2.6.0为例 部分概念包含笔者个人理解,如有遗漏或错误,欢迎评论或私信指正。 截图和程序部分引用自北京大学机器学习公开课 通过学习已经掌握了主要的基础函数之后具备了搭建一个网络并使其正常运行的能力,那下一步我们还…...

鸿蒙开发现在就业前景怎样?
随着科技的不断进步,鸿蒙系统逐渐崭露头角,成为智能设备领域的一颗新星。作为华为自主研发的操作系统,鸿蒙系统拥有着广阔的市场前景和就业机会。那么,鸿蒙开发的就业前景究竟怎样呢? 一、市场需求持续增长 随着鸿蒙…...
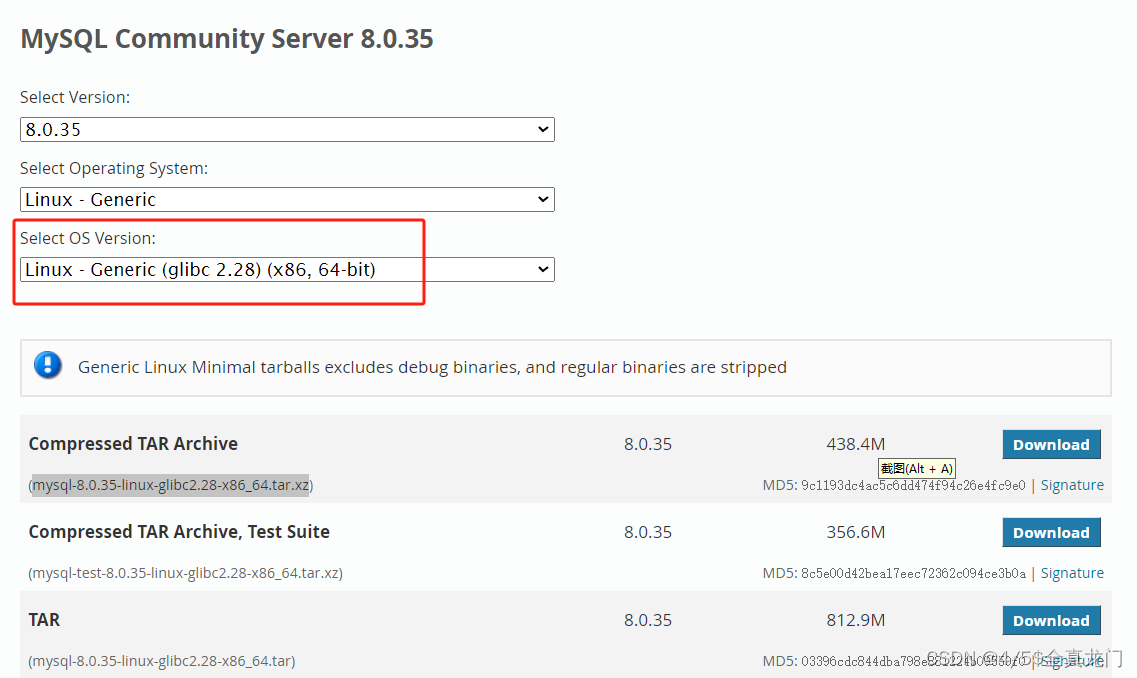
试用统信服务器操作系统UOS 20
作者:田逸(formyz) 试用统信Linux操作系统UOS,想了解一下用已有的Linux经验能否轻松驾驭它。以便在某些场景下,可以多一种选择。本次试验在Proxmox VE 8(以下简称PVE 8)平台下进行,采…...
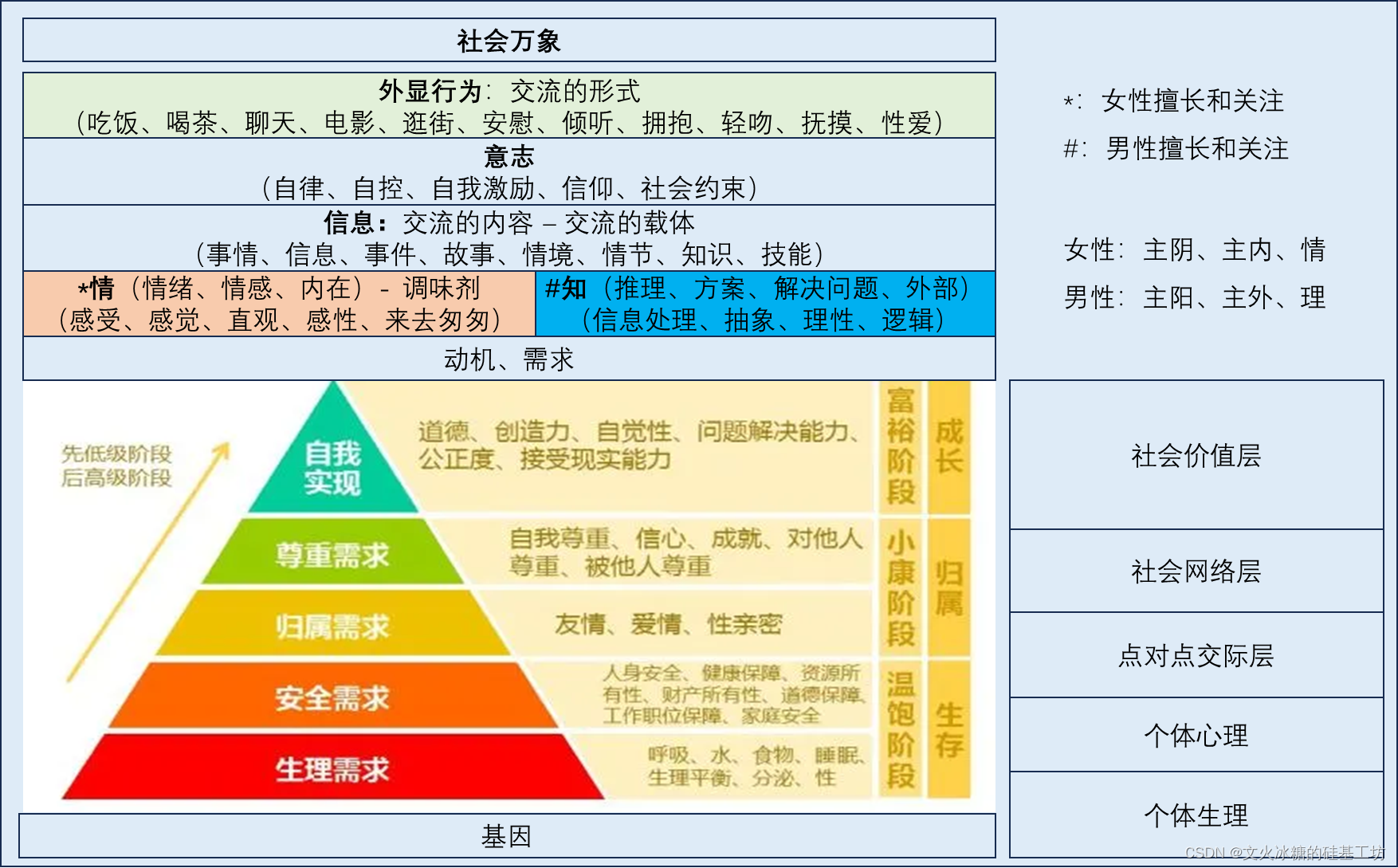
[情商-11]:人际交流的心理架构与需求层次模型
目录 前言: 一、心理架构 1.1 个体生理层 1.2 个体心理层 1.3 点对点人际交流层 1.4 社会网络层 1.5 社会价值层 二、人的需求层次模型 2.1 需求(欲望)层次模型 2.2 基因与人需求之间的关系 2.3 个体生理需求 2.4 个体的心理需求…...

【.NET Core】Lazy<T> 实现延迟加载详解
【.NET Core】Lazy 实现延迟加载详解 文章目录 【.NET Core】Lazy<T> 实现延迟加载详解一、概述二、Lazy<T>是什么三、Lazy基本用法3.1 构造时使用默认的初始化方式3.2 构造时使用指定的委托初始化 四、Lazy.Value使用五、Lazy扩展用法5.1 实现延迟属性5.2 Lazy实现…...
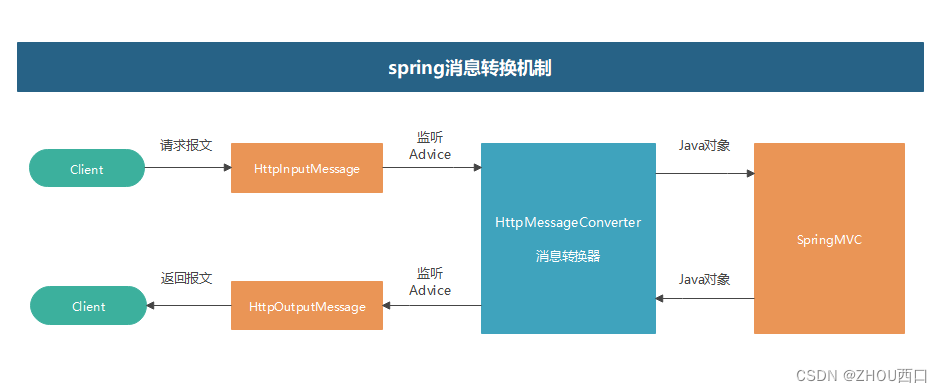
坑记(HttpInputMessage)
一、背景知识 public interface HttpInputMessage extends HttpMessage Represents an HTTP input message, consisting of headers and a readable body.Typically implemented by an HTTP request on the server-side, or a response on the client-side.Since: 3.0 Author:…...

day04打卡
day04打卡 面试题 02.07. 链表相交 时间复杂度:O(N),空间复杂度:O(1) 第一想法:求出两个链表长度,走差距步,再遍历找有没有相交 /*** Definition for singly-linked list.* struct ListNode {* int…...

语义分割miou指标计算详解
文章目录 1. 语义分割的评价指标2. 混淆矩阵计算2.1 np.bincount的使用2.2 混淆矩阵计算 3. 语义分割指标计算3.1 IOU计算方式1(推荐)方式2 3.2 Precision 计算3.3 总体的Accuracy计算3.4 Recall 计算3.5 MIOU计算 参考 MIoU全称为Mean Intersection over Union,平均…...
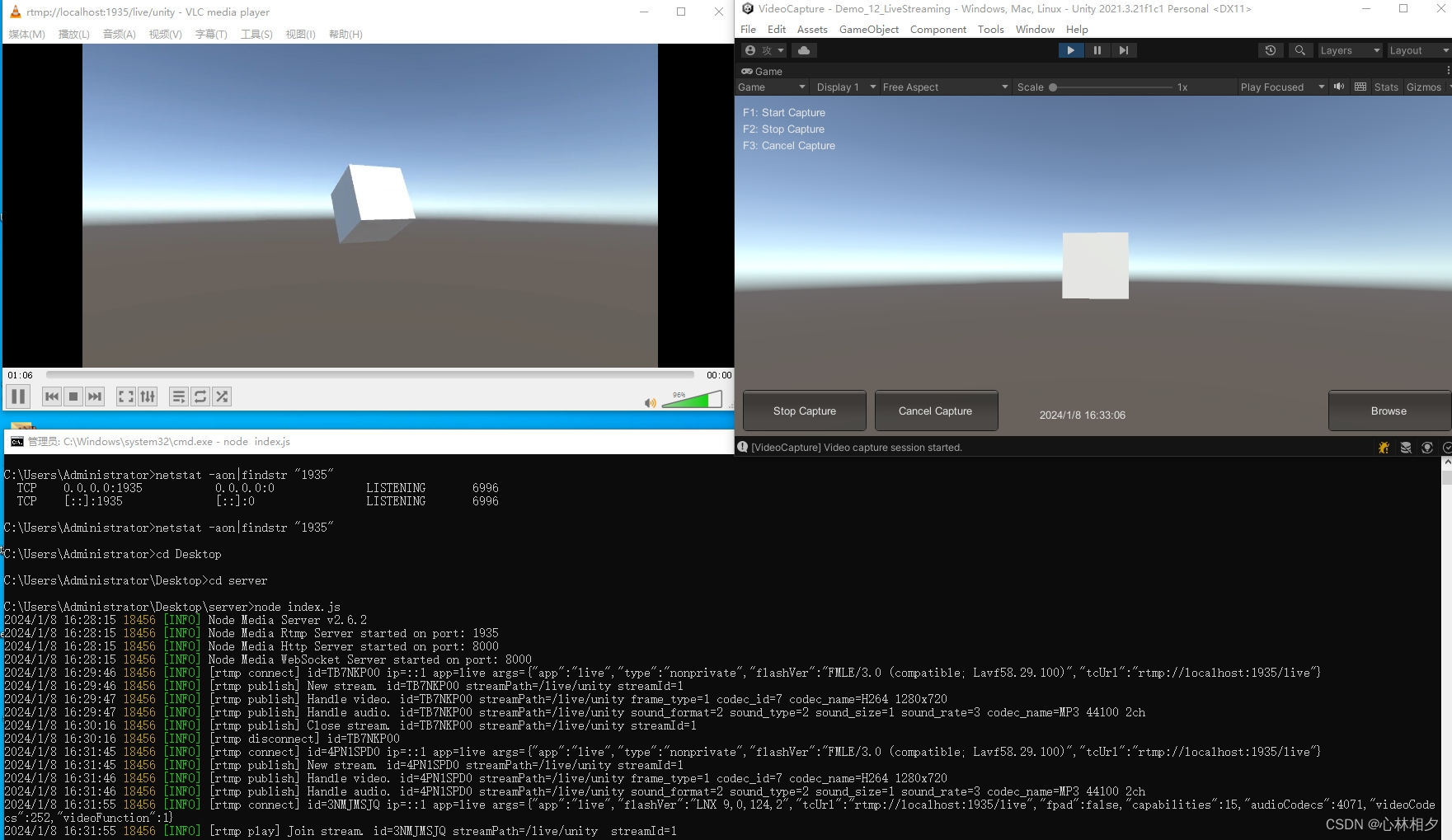
Unity3d 实现直播功能(无需sdk接入)
Unity3d 实现直播功能 需要插件 :VideoCapture 插件地址(免费的就行) 原理:客户端通过 VideoCapture 插件实现推流nodejs视频流转服务进行转发,播放器实现rtmp拉流 废话不多说,直接上 CaptureSource我选择的是屏幕录制,也可以是其他源 CaptureType选择LIVE–直播形式 LiveSt…...
计算机缺失msvcr100.dll如何修复?分享五种实测靠谱的方法
在计算机系统的日常运行与维护过程中,我们可能会遇到一种特定的故障场景,即系统中关键性动态链接库文件msvcr100.dll的丢失。msvcr100.dll是Microsoft Visual C Redistributable Package的一部分,对于许多基于Windows的应用程序来说ÿ…...
面试宝典进阶之redis缓存面试题
R1、【初级】Redis常用的数据类型有哪些? (1)String(字符串) (2)Hash(哈希) (3)List(列表) (4)Se…...

调试(c语言)
前言: 我们在写程序的时候可能多多少少都会出现一些bug,使我们的程序不能正常运行,所以为了更快更好的找到并修复bug,使这些问题迎刃而解,学习好如何调试代码是每个学习编程的人所必备的技能。 1. 什么是bug…...
opencv-4.8.0编译及使用
1 编译 opencv的编译总体来说比较简单,但必须记住一点:opencv的版本必须和opencv_contrib的版本保持一致。例如opencv使用4.8.0,opencv_contrib也必须使用4.8.0。 进入opencv和opencv_contrib的github页面后,默认看到的是git分支&…...

Jmeter 性能-监控服务器
Jmeter监控Linux需要三个文件 JMeterPlugins-Extras.jar (包:JMeterPlugins-Extras-1.4.0.zip) JMeterPlugins-Standard.jar (包:JMeterPlugins-Standard-1.4.0.zip) ServerAgent-2.2.3.zip 1、Jemter 安装插件 在插件管理中心的搜索Servers Perform…...
Excel学习
文章目录 学习链接Excel1. Excel的两种形式2. 常见excel操作工具3.POI1. POI的概述2. POI的应用场景3. 使用1.使用POI创建excel2.创建单元格写入内容3.单元格样式处理4.插入图片5.读取excel并解析图解POI 4. 基于模板输出POI报表5. 自定义POI导出工具类ExcelAttributeExcelExpo…...

【技能---labelme软件的安装及其使用--ubuntu】
文章目录 概要Labelme 是什么?Labelme 能干啥? Ubuntu20.04安装Labelme1.Anaconda的安装2.Labelme的安装3.Labelme的使用 概要 图像检测需要自己的数据集,为此需要对一些数据进行数据标注,这里提供了一种图像的常用标注工具——la…...

C++初阶-list的底层
目录 1.std::list实现的所有代码 2.list的简单介绍 2.1实现list的类 2.2_list_iterator的实现 2.2.1_list_iterator实现的原因和好处 2.2.2_list_iterator实现 2.3_list_node的实现 2.3.1. 避免递归的模板依赖 2.3.2. 内存布局一致性 2.3.3. 类型安全的替代方案 2.3.…...

UE5 学习系列(三)创建和移动物体
这篇博客是该系列的第三篇,是在之前两篇博客的基础上展开,主要介绍如何在操作界面中创建和拖动物体,这篇博客跟随的视频链接如下: B 站视频:s03-创建和移动物体 如果你不打算开之前的博客并且对UE5 比较熟的话按照以…...

2024年赣州旅游投资集团社会招聘笔试真
2024年赣州旅游投资集团社会招聘笔试真 题 ( 满 分 1 0 0 分 时 间 1 2 0 分 钟 ) 一、单选题(每题只有一个正确答案,答错、不答或多答均不得分) 1.纪要的特点不包括()。 A.概括重点 B.指导传达 C. 客观纪实 D.有言必录 【答案】: D 2.1864年,()预言了电磁波的存在,并指出…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个医院挂号小程序
一、开发准备 环境搭建: 安装DevEco Studio 3.0或更高版本配置HarmonyOS SDK申请开发者账号 项目创建: File > New > Create Project > Application (选择"Empty Ability") 二、核心功能实现 1. 医院科室展示 /…...

springboot整合VUE之在线教育管理系统简介
可以学习到的技能 学会常用技术栈的使用 独立开发项目 学会前端的开发流程 学会后端的开发流程 学会数据库的设计 学会前后端接口调用方式 学会多模块之间的关联 学会数据的处理 适用人群 在校学生,小白用户,想学习知识的 有点基础,想要通过项…...

Java数值运算常见陷阱与规避方法
整数除法中的舍入问题 问题现象 当开发者预期进行浮点除法却误用整数除法时,会出现小数部分被截断的情况。典型错误模式如下: void process(int value) {double half = value / 2; // 整数除法导致截断// 使用half变量 }此时...

go 里面的指针
指针 在 Go 中,指针(pointer)是一个变量的内存地址,就像 C 语言那样: a : 10 p : &a // p 是一个指向 a 的指针 fmt.Println(*p) // 输出 10,通过指针解引用• &a 表示获取变量 a 的地址 p 表示…...
)
华为OD最新机试真题-数组组成的最小数字-OD统一考试(B卷)
题目描述 给定一个整型数组,请从该数组中选择3个元素 组成最小数字并输出 (如果数组长度小于3,则选择数组中所有元素来组成最小数字)。 输入描述 行用半角逗号分割的字符串记录的整型数组,0<数组长度<= 100,0<整数的取值范围<= 10000。 输出描述 由3个元素组成…...

电脑桌面太单调,用Python写一个桌面小宠物应用。
下面是一个使用Python创建的简单桌面小宠物应用。这个小宠物会在桌面上游荡,可以响应鼠标点击,并且有简单的动画效果。 import tkinter as tk import random import time from PIL import Image, ImageTk import os import sysclass DesktopPet:def __i…...

2025-05-08-deepseek本地化部署
title: 2025-05-08-deepseek 本地化部署 tags: 深度学习 程序开发 2025-05-08-deepseek 本地化部署 参考博客 本地部署 DeepSeek:小白也能轻松搞定! 如何给本地部署的 DeepSeek 投喂数据,让他更懂你 [实验目的]:理解系统架构与原…...






