语义分割miou指标计算详解
文章目录
- 1. 语义分割的评价指标
- 2. 混淆矩阵计算
- 2.1 np.bincount的使用
- 2.2 混淆矩阵计算
- 3. 语义分割指标计算
- 3.1 IOU计算
- 方式1(推荐)
- 方式2
- 3.2 Precision 计算
- 3.3 总体的Accuracy计算
- 3.4 Recall 计算
- 3.5 MIOU计算
- 参考
MIoU全称为Mean Intersection over Union,平均交并比。可作为语义分割系统性能的评价指标。
- P:Prediction预测值
- G:Ground Truth真实值

其中IOU: 交并比就是该类的真实标签和预测值的交和并的比值

单类的交并比可以理解为下图:

1. 语义分割的评价指标
True Positive (
TP): 把正样本成功预测为正。
True Negative (TN):把负样本成功预测为负。
False Positive (FP):把负样本错误地预测为正。
False Negative (FN):把正样本错误的预测为负。
-
(1) Accuracy准确率,指的是“预测正确的样本数÷样本数总数”。计算公式为:
A c c u r a c y = T P + T N T P + T N + F P + F N Accuracy = \frac{TP+TN}{TP+TN+FP+FN} Accuracy=TP+TN+FP+FNTP+TN -
(2) Precision精确率或者精度,指的是预测为Positive的样本,占所有预测样本的比率
P r e c i s i o n = T P T P + F P Precision= \frac{TP}{TP+FP} Precision=TP+FPTP -
(3)Recall召回率,指的是预测为Positive的样本,占所有Positive样本的比率
P r e c i s i o n = T P P Precision= \frac{TP}{P} Precision=PTP -
(4) F1 score: 综合考虑了precision和recall两方面的因素,做到了对于两者的调和,即:既要“求精”也要“求全”,做到不偏科。
F 1 s c o r e = 2 ∗ p r e c i s i o n ∗ r e c a l l p r e c i s i o n + r e c a l l F1 score= \frac{2*precision*recall}{precision+recall} F1score=precision+recall2∗precision∗recall
- (5)
MIOU作为为语义分割最重要标准度量。其计算两个集合的交集和并集之比,在语义分割的问题中,这两个集合为真实值和预测值。在每个类上计算IoU,之后平均。计算公式如下
M I O U = 1 k + 1 ∑ i = 0 k T P F N + F P + T P MIOU =\frac{1}{k+1}\sum_{i=0}^{k}\frac{TP}{FN+FP+TP} MIOU=k+11i=0∑kFN+FP+TPTP
等价于:
M I O U = 1 k + 1 ∑ i = 0 k p i i ∑ j = 0 k p i j + ∑ j = 0 k p j i − p i i MIOU=\frac{1}{k+1}\sum_{i=0}^{k}\frac{p_{ii}}{\sum_{j=0}^k p_{ij} + \sum_{j=0}^k p_{ji} -p_{ii}} MIOU=k+11i=0∑k∑j=0kpij+∑j=0kpji−piipii
其中: p i i p_{ii} pii 真实为类别i,预测也为i的像素个数,也就是正确预测的像素个数TP; p i j p_{ij} pij表示真实为类别i,但预测为类别j的像素个数,也就是FN; p j i p_{ji} pji表示真实为类别j,但预测为类别i的像素个数, 也就是FP
注意: 对于多分类,TN为0 ,即没有所谓的负样本
2. 混淆矩阵计算
- 计算
MIoU,我们需要借助混淆矩阵来进行计算。 混淆矩阵就是统计分类模型的分类结果,即:统计归对类,归错类的样本的个数,然后把结果放在一个表里展示出来,这个表就是混淆矩阵- 其
每一列代表预测值(pred),每一行代表的是实际的类别(gt)

对角都对TP,横看真实,竖看预测: 每一行之和,为该行对应类(如Cat)的总数;每一列之和为该列对应类别的预测的总数。
2.1 np.bincount的使用
在计算混淆矩阵时,可以利用np.bincount函数方便我们计算。
numpy.bincount(x, weights=None, minlength=None)
- 该方法返回每个索引值在x中出现的次数
- 给一个向量
x,x中最大的元素记为j,返回一个向量1行j+1列的向量y,y[i]代表i在x中出现的次数
#x中最大的数为7,那么它的索引值为0->7
x = np.array([0, 1, 1, 3, 2, 1, 7])
#索引0出现了1次,索引1出现了3次......索引5出现了0次......
np.bincount(x)
#因此,输出结果为:array([1, 3, 1, 1, 0, 0, 0, 1])
minlength也是一个常用的参数,表示输出的数组长度至少为minlength,如果x中最大的元素加1大于数组长度,那么数组的长度以x中最大元素加1为准(例如,如果数组中最大元素为3,minlength=5,那么数组的长度为5;如果数组中最大元素为7,minlength=5,那么数组的最大长度为7+1=8,这里之所以加1是因为元素0也占了一个索引)。举个例子说明:
# a中最大的数为3,因此数组长度为4,那么它的索引值为0->3
a = np.array([2, 2, 1, 3 ])
# 本来数组的长度为4,但指定了minlength为7,因此现在数组长度为7(多的补0),所以现在它的索引值为0->6
np.bincount(x, minlength=7)
# 输出结果为:array([0, 1, 2, 1, 0, 0, 0])# a中最大的数为4,因此bin的数量为5,那么它的索引值为0->4
x = np.array([4, 2, 3, 1, 2])
# 数组的长度原本为5,但指定了minlength为1,因为5 > 1,所以这个参数不起作用,索引值还是0->4
np.bincount(x, minlength=1)
# 输出结果为:array([0, 1, 2, 1,1])
2.2 混淆矩阵计算
# 设标签宽W,长H
def fast_hist(a, b, n):#--------------------------------------------------------------------------------## a是转化成一维数组的标签,形状(H×W,);b是转化成一维数组的预测结果,形状(H×W,)#--------------------------------------------------------------------------------#k = (a >= 0) & (a < n)#--------------------------------------------------------------------------------## np.bincount计算了从0到n**2-1这n**2个数中每个数出现的次数,返回值形状(n, n)# 返回中,写对角线上的为分类正确的像素点#--------------------------------------------------------------------------------#return np.bincount(n * a[k].astype(int) + b[k], minlength=n ** 2).reshape(n, n)
- 产生
n×n的混淆矩阵统计表参数a:即:真实的标签gt, 需要reshape为一行输入参数b:即预测的标签pred,它是经过argmax输出的预测8位标签图,每个像素表示为类别索引(reshape为一行输入),参数n:类别数cls_num
- 首先过滤
gt中,类别超过n的索引,确保gt的分类都包含在n个类别中
k = (a >= 0) & (a < n)
- 如果要去掉背景,不将背景计算在混淆矩阵,则可以写为:
k = (a > 0) & (a < n) #去掉了背景,假设0是背景- 然后利用
np.bincount生成元素个数为n*n的数组,并且reshape为 n × n n \times n n×n的混淆矩阵,这样确保混淆矩阵行和列都为类别class的个数n n*n数组中,每个元素的值,表示为0~n*n的索引值在x中出现的次数,这样就获得了最终混淆矩阵。这里的x表示为n * a[k] + b[k],为啥这么定义呢?,
举例如下:将图片的gt标签a和pred输出图片b,都转换为一行; a和b中每个元素代表类别索引

- 前面
8, 9, 4, 7, 6都预测正确, 对于预测正确的像素来说,n * a + b就是对角线的值; 假设n=10,有10类。n * a + b就是88, 99, 44, 77, 66 - 紧接着6预测成了5, 因此n * a + b就是65
- 88, 99, 44, 77, 66就是对角线上的值(
如下图红框,65就是预测错误,并且能真实反映把6预测成了5(如下图蓝框)

3. 语义分割指标计算

3.1 IOU计算
方式1(推荐)
计算每个类别的IOU计算:
I O U = T P F N + F P + T P IOU =\frac{TP}{FN+FP+TP} IOU=FN+FP+TPTP
def per_class_iu(hist):return np.diag(hist) / np.maximum((hist.sum(1) + hist.sum(0) - np.diag(hist)), 1)
输入hist表示 2维的混淆矩阵,大小为n*n(n为类别数)- 混淆矩阵
对角线元素值,表示每个类别预测正确的数TP:
np.diag(hist)
- 其中:混淆矩阵所对应
行中,每一行为对应类别(如类1)的统计值中,对角线位置为正常预测为该类别的统计值(TP),其他位置则是错误的将该类别预测为其他的类别FN: 因此每个类别的FP统计值为:
FN =hist.sum(1) -TP = hist.sum(1) - np.diag(hist)
- 同理,预测为该类别所对应的
列中,对角线为正确预测,其他位置则是将其他类别错误的预测为该列所对应的类别,也就是FP
FP =hist.sum(0) -TP = hist.sum(0) - np.diag(hist)
因此分母FN_FP+TP=np.maximum(hist.sum(1) + hist.sum(0) - np.diag(hist),1), 这里加上np.maximum确保了分母不为0
方式2
def IOU(pred,target,n_classes = args.num_class ):ious = []# ignore IOU for background classfor cls in range(1,n_classes):pred_inds = pred == clstarget_inds = target == cls# target_sum = target_inds.sum()intersection = (pred_inds[target_inds]).sum()union = pred_inds.sum() + target_inds.sum() - intersectionif union == 0:ious.append(float('nan')) # If there is no ground truth,do not include in evaluationelse:ious.append(float(intersection)/float(max(union,1)))return ious
参考:https://github.com/dilligencer-zrj/code_zoo/blob/master/compute_mIOU
3.2 Precision 计算
每个类别的Precision 计算如下:
P r e c i s i o n = T P T P + F P Precision= \frac{TP}{TP+FP} Precision=TP+FPTP
def per_class_Precision(hist):return np.diag(hist) / np.maximum(hist.sum(0), 1)
- 其中
np.diag(hist)为TP值,hist.sum(0)表示为TP+FP,np.maximum确保确保分母不为0
3.3 总体的Accuracy计算
总体的Accuracy计算如下:
A c c u r a c y = T P + T N T P + T N + F P + F N Accuracy = \frac{TP+TN}{TP+TN+FP+FN} Accuracy=TP+TN+FP+FNTP+TN
由于是多类别,没有负样本,因此TN为0。
def per_Accuracy(hist):return np.sum(np.diag(hist)) / np.maximum(np.sum(hist), 1)
3.4 Recall 计算
recall指的是预测为Positive的样本,占所有Positive样本的比率
P r e c i s i o n = T P P Precision= \frac{TP}{P} Precision=PTP
def per_class_PA_Recall(hist):return np.diag(hist) / np.maximum(hist.sum(1), 1)
- 每一行统计值为该类别样本的真实数量P, 因此
P = hist.sum(1)
3.5 MIOU计算
def compute_mIoU(gt_dir, pred_dir, png_name_list, num_classes, name_classes=None): print('Num classes', num_classes) #-----------------------------------------## 创建一个全是0的矩阵,是一个混淆矩阵#-----------------------------------------#hist = np.zeros((num_classes, num_classes))#------------------------------------------------## 获得验证集标签路径列表,方便直接读取# 获得验证集图像分割结果路径列表,方便直接读取#------------------------------------------------#gt_imgs = [join(gt_dir, x + ".png") for x in png_name_list] pred_imgs = [join(pred_dir, x + ".png") for x in png_name_list] #------------------------------------------------## 读取每一个(图片-标签)对#------------------------------------------------#for ind in range(len(gt_imgs)): #------------------------------------------------## 读取一张图像分割结果,转化成numpy数组#------------------------------------------------#pred = np.array(Image.open(pred_imgs[ind])) #------------------------------------------------## 读取一张对应的标签,转化成numpy数组#------------------------------------------------#label = np.array(Image.open(gt_imgs[ind])) # 如果图像分割结果与标签的大小不一样,这张图片就不计算if len(label.flatten()) != len(pred.flatten()): print('Skipping: len(gt) = {:d}, len(pred) = {:d}, {:s}, {:s}'.format(len(label.flatten()), len(pred.flatten()), gt_imgs[ind],pred_imgs[ind]))continue#------------------------------------------------## 对一张图片计算21×21的hist矩阵,并累加#------------------------------------------------#hist += fast_hist(label.flatten(), pred.flatten(), num_classes) # 每计算10张就输出一下目前已计算的图片中所有类别平均的mIoU值if name_classes is not None and ind > 0 and ind % 10 == 0: print('{:d} / {:d}: mIou-{:0.2f}%; mPA-{:0.2f}%; Accuracy-{:0.2f}%'.format(ind, len(gt_imgs),100 * np.nanmean(per_class_iu(hist)),100 * np.nanmean(per_class_PA_Recall(hist)),100 * per_Accuracy(hist)))#------------------------------------------------## 计算所有验证集图片的逐类别mIoU值#------------------------------------------------#IoUs = per_class_iu(hist)PA_Recall = per_class_PA_Recall(hist)Precision = per_class_Precision(hist)#------------------------------------------------## 逐类别输出一下mIoU值#------------------------------------------------#if name_classes is not None:for ind_class in range(num_classes):print('===>' + name_classes[ind_class] + ':\tIou-' + str(round(IoUs[ind_class] * 100, 2)) \+ '; Recall (equal to the PA)-' + str(round(PA_Recall[ind_class] * 100, 2))+ '; Precision-' + str(round(Precision[ind_class] * 100, 2)))#-----------------------------------------------------------------## 在所有验证集图像上求所有类别平均的mIoU值,计算时忽略NaN值#-----------------------------------------------------------------#print('===> mIoU: ' + str(round(np.nanmean(IoUs) * 100, 2)) + '; mPA: ' + str(round(np.nanmean(PA_Recall) * 100, 2)) + '; Accuracy: ' + str(round(per_Accuracy(hist) * 100, 2))) return np.array(hist, np.int), IoUs, PA_Recall, Precision
- 首先创建一个维度为
(num_classes, num_classes)的空混淆矩阵hist - 遍历
pred_imgs和gt_imgs, 将遍历得到的每一张pred和label展平(flatten)到一维,输入到fast_hist计算单张图片预测的混淆矩阵,将每次的计算结果加到总的混淆矩阵hist中
for ind in range(len(gt_imgs)): #------------------------------------------------## 读取一张图像分割结果,转化成numpy数组#------------------------------------------------#pred = np.array(Image.open(pred_imgs[ind])) #------------------------------------------------## 读取一张对应的标签,转化成numpy数组#------------------------------------------------#label = np.array(Image.open(gt_imgs[ind])) # 如果图像分割结果与标签的大小不一样,这张图片就不计算if len(label.flatten()) != len(pred.flatten()): print('Skipping: len(gt) = {:d}, len(pred) = {:d}, {:s}, {:s}'.format(len(label.flatten()), len(pred.flatten()), gt_imgs[ind],pred_imgs[ind]))continue#------------------------------------------------## 对一张图片计算21×21的hist矩阵,并累加#------------------------------------------------#hist += fast_hist(label.flatten(), pred.flatten(), num_classes)
- 每
计算10张就输出一下目前已计算的图片中所有类别平均的mIoU值
# 每计算10张就输出一下目前已计算的图片中所有类别平均的mIoU值if name_classes is not None and ind > 0 and ind % 10 == 0: print('{:d} / {:d}: mIou-{:0.2f}%; mPA-{:0.2f}%; Accuracy-{:0.2f}%'.format(ind, len(gt_imgs),100 * np.nanmean(per_class_iu(hist)),100 * np.nanmean(per_class_PA_Recall(hist)),100 * per_Accuracy(hist)))
- 遍历完成后,得到所有类别的Iou值
IoUs以及PA_Recall和Precision,并逐类别输出一下mIoU值
if name_classes is not None:for ind_class in range(num_classes):print('===>' + name_classes[ind_class] + ':\tIou-' + str(round(IoUs[ind_class] * 100, 2)) \+ '; Recall (equal to the PA)-' + str(round(PA_Recall[ind_class] * 100, 2))+ '; Precision-' + str(round(Precision[ind_class] * 100, 2)))
- 最后在所有验证集图像上求所有类别平均的mIoU值
print('===> mIoU: ' + str(round(np.nanmean(IoUs) * 100, 2)) + '; mPA: ' + str(round(np.nanmean(PA_Recall) * 100, 2)) + '; Accuracy: ' + str(round(per_Accuracy(hist) * 100, 2)))
参考
- https://github.com/bubbliiiing/deeplabv3-plus-pytorch/blob/main/utils/utils_metrics.py
- https://github.com/dilligencer-zrj/code_zoo/blob/master/compute_mIOU
- https://www.jianshu.com/p/42939bf83b8a
相关文章:

语义分割miou指标计算详解
文章目录 1. 语义分割的评价指标2. 混淆矩阵计算2.1 np.bincount的使用2.2 混淆矩阵计算 3. 语义分割指标计算3.1 IOU计算方式1(推荐)方式2 3.2 Precision 计算3.3 总体的Accuracy计算3.4 Recall 计算3.5 MIOU计算 参考 MIoU全称为Mean Intersection over Union,平均…...
Unity3d 实现直播功能(无需sdk接入)
Unity3d 实现直播功能 需要插件 :VideoCapture 插件地址(免费的就行) 原理:客户端通过 VideoCapture 插件实现推流nodejs视频流转服务进行转发,播放器实现rtmp拉流 废话不多说,直接上 CaptureSource我选择的是屏幕录制,也可以是其他源 CaptureType选择LIVE–直播形式 LiveSt…...
计算机缺失msvcr100.dll如何修复?分享五种实测靠谱的方法
在计算机系统的日常运行与维护过程中,我们可能会遇到一种特定的故障场景,即系统中关键性动态链接库文件msvcr100.dll的丢失。msvcr100.dll是Microsoft Visual C Redistributable Package的一部分,对于许多基于Windows的应用程序来说ÿ…...
面试宝典进阶之redis缓存面试题
R1、【初级】Redis常用的数据类型有哪些? (1)String(字符串) (2)Hash(哈希) (3)List(列表) (4)Se…...

调试(c语言)
前言: 我们在写程序的时候可能多多少少都会出现一些bug,使我们的程序不能正常运行,所以为了更快更好的找到并修复bug,使这些问题迎刃而解,学习好如何调试代码是每个学习编程的人所必备的技能。 1. 什么是bug…...
opencv-4.8.0编译及使用
1 编译 opencv的编译总体来说比较简单,但必须记住一点:opencv的版本必须和opencv_contrib的版本保持一致。例如opencv使用4.8.0,opencv_contrib也必须使用4.8.0。 进入opencv和opencv_contrib的github页面后,默认看到的是git分支&…...

Jmeter 性能-监控服务器
Jmeter监控Linux需要三个文件 JMeterPlugins-Extras.jar (包:JMeterPlugins-Extras-1.4.0.zip) JMeterPlugins-Standard.jar (包:JMeterPlugins-Standard-1.4.0.zip) ServerAgent-2.2.3.zip 1、Jemter 安装插件 在插件管理中心的搜索Servers Perform…...
Excel学习
文章目录 学习链接Excel1. Excel的两种形式2. 常见excel操作工具3.POI1. POI的概述2. POI的应用场景3. 使用1.使用POI创建excel2.创建单元格写入内容3.单元格样式处理4.插入图片5.读取excel并解析图解POI 4. 基于模板输出POI报表5. 自定义POI导出工具类ExcelAttributeExcelExpo…...

【技能---labelme软件的安装及其使用--ubuntu】
文章目录 概要Labelme 是什么?Labelme 能干啥? Ubuntu20.04安装Labelme1.Anaconda的安装2.Labelme的安装3.Labelme的使用 概要 图像检测需要自己的数据集,为此需要对一些数据进行数据标注,这里提供了一种图像的常用标注工具——la…...

回归预测 | Matlab实现SSA-CNN-LSTM-Attention麻雀优化卷积长短期记忆神经网络注意力机制多变量回归预测(SE注意力机制)
回归预测 | Matlab实现SSA-CNN-LSTM-Attention麻雀优化卷积长短期记忆神经网络注意力机制多变量回归预测(SE注意力机制) 目录 回归预测 | Matlab实现SSA-CNN-LSTM-Attention麻雀优化卷积长短期记忆神经网络注意力机制多变量回归预测(SE注意力…...

css垂直水平居中的几种实现方式
垂直水平居中的几种实现方式 一、固定宽高: 1、定位 margin-top margin-left .box-container{position: relative;width: 300px;height: 300px;}.box-container .box {width: 200px; height: 100px;position: absolute; left: 50%; top: 50%;margin-top: -50px;…...

OpenHarmony之hdc
OpenHarmony之hdc 简介 hdc(OpenHarmony Device Connector)是 OpenHarmony 为开发人员提供的用于调试的命令行工具,通过该工具可以在Windows/Linux/MacOS等系统上与开发机或者模拟器进行交互。 类似于Android的adb,和adb类似&a…...
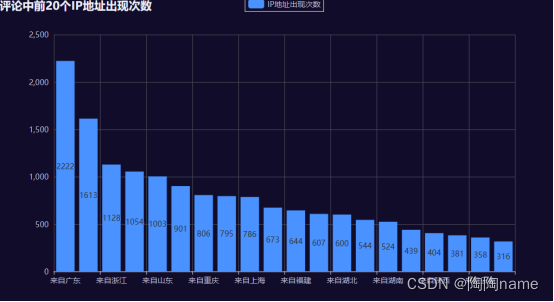
【爬虫实战】-爬取微博之夜盛典评论,爬取了1.7w条数据
前言: TaoTao之前在前几期推文中发布了一个篇weibo评论的爬虫。主要就是采集评论区的数据,包括评论、评论者ip、评论id、评论者等一些信息。然后有很多的小伙伴对这个代码很感兴趣。TaoTao也都给代码开源了。由于比较匆忙,所以没来得及去讲这…...

CST2024的License服务成功启动,仍报错——“The desired daemon is down...”,适用于任何版本!基础设置遗漏!
CST2024的License服务成功启动,仍报错——“The desired daemon is down…”,适用于任何版本!基础设置遗漏! CST2024的License服务成功启动后报错 若不能成功启动License服务,有可能是你的计算机名称带中文ÿ…...

matlab中any()函数用法
一、帮助文档中的介绍 B any(A) 沿着大小不等于 1 的数组 A 的第一维测试所有元素为非零数字还是逻辑值 1 (true)。实际上,any 是逻辑 OR 运算符的原生扩展。 二、解读 分两步走: ①确定维度;②确定运算规则 以下面二维数组为例 >>…...
Apache ECharts | 一个数据可视化图表库
文章目录 1、简介1.1、主要特点1.2、使用场景 2、安装方式一:从下载的源代码或编译产物安装方法二:从 npm 安装方法三:⭐定制安装echarts.js 3、使用 官网: 英语:https://echarts.apache.org/en/index.html 中文&a…...
m1 + swoole(hyperf) + yasd + phpstorm 安装和debug
参考文档 Mac M1安装报错 checking for boost... configure: error: lib boost not found. Try: install boost library Issue #89 swoole/yasd GitHub 1.安装boost库 brew install boostbrew link boost 2.下载yasd git clone https://github.com/swoole/yasd.git 3.编…...
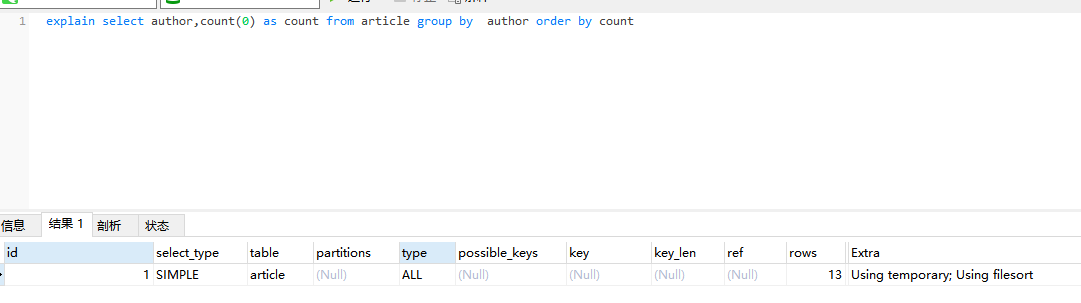
group by 查询慢的话,如何优化?
1、说明 根据一定的规则,进行分组。 group by可能会慢在哪里?因为它既用到临时表,又默认用到排序。有时候还可能用到磁盘临时表。 如果执行过程中,会发现内存临时表大小到达了上限(控制这个上限的参数就是tmp_table…...

【重学C语言】一、C语言简介
【重学C语言】一、C语言简介 什么是编程语言?编程语言 C语言发展史C语言标准变迁开发软件CLion安装步骤 VIsual Studio安装步骤 Clion 和 VS2022 绑定 电脑常识 什么是编程语言? 人类语言:语言就是人类进行沟通交流的表达方式,应…...
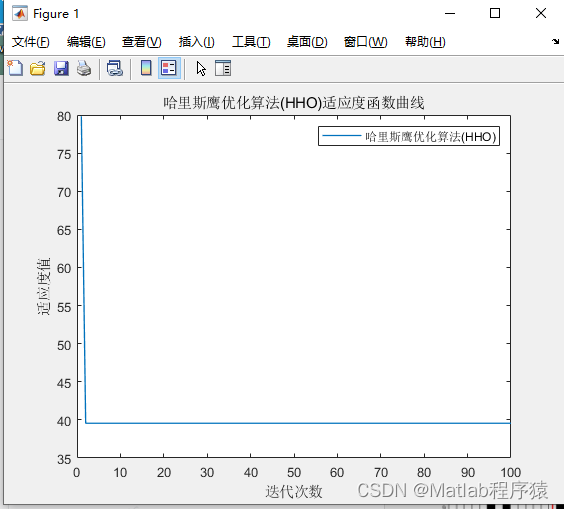
【MATLAB源码-第109期】基于matlab的哈里斯鹰优化算发(HHO)机器人栅格路径规划,输出做短路径图和适应度曲线。
操作环境: MATLAB 2022a 1、算法描述 哈里斯鹰优化算法(Harris Hawk Optimization, HHO)是一种受自然界捕食行为启发的优化算法。它基于哈里斯鹰的捕猎策略和行为模式,主要用于解决各种复杂的优化问题。这个算法的核心特征在于…...

【网络】每天掌握一个Linux命令 - iftop
在Linux系统中,iftop是网络管理的得力助手,能实时监控网络流量、连接情况等,帮助排查网络异常。接下来从多方面详细介绍它。 目录 【网络】每天掌握一个Linux命令 - iftop工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景…...

uni-app学习笔记二十二---使用vite.config.js全局导入常用依赖
在前面的练习中,每个页面需要使用ref,onShow等生命周期钩子函数时都需要像下面这样导入 import {onMounted, ref} from "vue" 如果不想每个页面都导入,需要使用node.js命令npm安装unplugin-auto-import npm install unplugin-au…...

UE5 学习系列(三)创建和移动物体
这篇博客是该系列的第三篇,是在之前两篇博客的基础上展开,主要介绍如何在操作界面中创建和拖动物体,这篇博客跟随的视频链接如下: B 站视频:s03-创建和移动物体 如果你不打算开之前的博客并且对UE5 比较熟的话按照以…...

【项目实战】通过多模态+LangGraph实现PPT生成助手
PPT自动生成系统 基于LangGraph的PPT自动生成系统,可以将Markdown文档自动转换为PPT演示文稿。 功能特点 Markdown解析:自动解析Markdown文档结构PPT模板分析:分析PPT模板的布局和风格智能布局决策:匹配内容与合适的PPT布局自动…...
)
postgresql|数据库|只读用户的创建和删除(备忘)
CREATE USER read_only WITH PASSWORD 密码 -- 连接到xxx数据库 \c xxx -- 授予对xxx数据库的只读权限 GRANT CONNECT ON DATABASE xxx TO read_only; GRANT USAGE ON SCHEMA public TO read_only; GRANT SELECT ON ALL TABLES IN SCHEMA public TO read_only; GRANT EXECUTE O…...

Cloudflare 从 Nginx 到 Pingora:性能、效率与安全的全面升级
在互联网的快速发展中,高性能、高效率和高安全性的网络服务成为了各大互联网基础设施提供商的核心追求。Cloudflare 作为全球领先的互联网安全和基础设施公司,近期做出了一个重大技术决策:弃用长期使用的 Nginx,转而采用其内部开发…...

令牌桶 滑动窗口->限流 分布式信号量->限并发的原理 lua脚本分析介绍
文章目录 前言限流限制并发的实际理解限流令牌桶代码实现结果分析令牌桶lua的模拟实现原理总结: 滑动窗口代码实现结果分析lua脚本原理解析 限并发分布式信号量代码实现结果分析lua脚本实现原理 双注解去实现限流 并发结果分析: 实际业务去理解体会统一注…...

解决本地部署 SmolVLM2 大语言模型运行 flash-attn 报错
出现的问题 安装 flash-attn 会一直卡在 build 那一步或者运行报错 解决办法 是因为你安装的 flash-attn 版本没有对应上,所以报错,到 https://github.com/Dao-AILab/flash-attention/releases 下载对应版本,cu、torch、cp 的版本一定要对…...

Axios请求超时重发机制
Axios 超时重新请求实现方案 在 Axios 中实现超时重新请求可以通过以下几种方式: 1. 使用拦截器实现自动重试 import axios from axios;// 创建axios实例 const instance axios.create();// 设置超时时间 instance.defaults.timeout 5000;// 最大重试次数 cons…...

ip子接口配置及删除
配置永久生效的子接口,2个IP 都可以登录你这一台服务器。重启不失效。 永久的 [应用] vi /etc/sysconfig/network-scripts/ifcfg-eth0修改文件内内容 TYPE"Ethernet" BOOTPROTO"none" NAME"eth0" DEVICE"eth0" ONBOOT&q…...
