day04打卡
day04打卡
面试题 02.07. 链表相交
时间复杂度:O(N),空间复杂度:O(1)
第一想法:求出两个链表长度,走差距步,再遍历找有没有相交
/*** Definition for singly-linked list.* struct ListNode {* int val;* ListNode *next;* ListNode(int x) : val(x), next(NULL) {}* };*/
class Solution {
public:ListNode *getIntersectionNode(ListNode *headA, ListNode *headB) {ListNode* a = headA, * b = headB;//求出 两个链表的长度int lenA = 0, lenB = 0;while(a != NULL) {lenA++;a = a->next;}while(b != NULL){lenB++;b = b->next;}a = headA, b = headB;//让两个链表长度统一//让a做长的链表if(lenA < lenB){swap(lenA, lenB);swap(a, b);}int n = lenA - lenB;//a走差距步while(n--){a = a->next;}//遍历链表,看看有没有相交while(a != NULL){if(a == b) return a;else {a = a->next;b = b->next;}}return NULL;}
};
19. 删除链表的倒数第 N 个结点
时间复杂度:O(N),空间复杂度:O(1)
第一想法:双指针,快指针先走n步,再同时走,走到快指针到空时,修改慢指针的连接即可
/*** Definition for singly-linked list.* struct ListNode {* int val;* ListNode *next;* ListNode() : val(0), next(nullptr) {}* ListNode(int x) : val(x), next(nullptr) {}* ListNode(int x, ListNode *next) : val(x), next(next) {}* };*/
class Solution {
public:ListNode* removeNthFromEnd(ListNode* head, int n) {ListNode* newHead = new ListNode;newHead->next = head;ListNode* fast = head, * slow = newHead;//快指针先走n步while(n--) fast = fast->next;//同时走,快指针到空时,slow就是倒数第n个节点while(fast != nullptr){fast = fast->next;slow = slow->next;}slow->next = slow->next->next;ListNode* ret = newHead->next;delete newHead;return ret;}
};
24. 两两交换链表中的节点 - 力扣(LeetCode)
时间复杂度:O(N),空间复杂度:O(1)
第一想法:迭代,设置一个虚拟头结点,设定三个指针,prev,cur,next。修改链表关系即可
困难:没有把握好三个指针的连接关系
看了题解:画图实现了三个指针的链接关系和递归解法
/*** Definition for singly-linked list.* struct ListNode {* int val;* ListNode *next;* ListNode() : val(0), next(nullptr) {}* ListNode(int x) : val(x), next(nullptr) {}* ListNode(int x, ListNode *next) : val(x), next(next) {}* };*/
class Solution {
public:ListNode* swapPairs(ListNode* head) {//迭代// if(head == nullptr || head->next == nullptr) return head;// ListNode* newHead = new ListNode;// newHead->next = head;// ListNode* prev = newHead, * cur = head, * next = head->next;// while(cur != nullptr && next != nullptr)// {// prev->next = next;// cur->next = next->next;// next->next = cur;// //交换节点// prev = cur;// cur = cur->next;// if(cur) next = cur->next;// }// return newHead->next;//递归//递归出口if(head == nullptr || head->next == nullptr) return head;//子问题ListNode* newHead = swapPairs(head->next->next);ListNode* ret = head->next;head->next = newHead;ret->next = head;return ret;}
};
相关文章:

day04打卡
day04打卡 面试题 02.07. 链表相交 时间复杂度:O(N),空间复杂度:O(1) 第一想法:求出两个链表长度,走差距步,再遍历找有没有相交 /*** Definition for singly-linked list.* struct ListNode {* int…...

语义分割miou指标计算详解
文章目录 1. 语义分割的评价指标2. 混淆矩阵计算2.1 np.bincount的使用2.2 混淆矩阵计算 3. 语义分割指标计算3.1 IOU计算方式1(推荐)方式2 3.2 Precision 计算3.3 总体的Accuracy计算3.4 Recall 计算3.5 MIOU计算 参考 MIoU全称为Mean Intersection over Union,平均…...
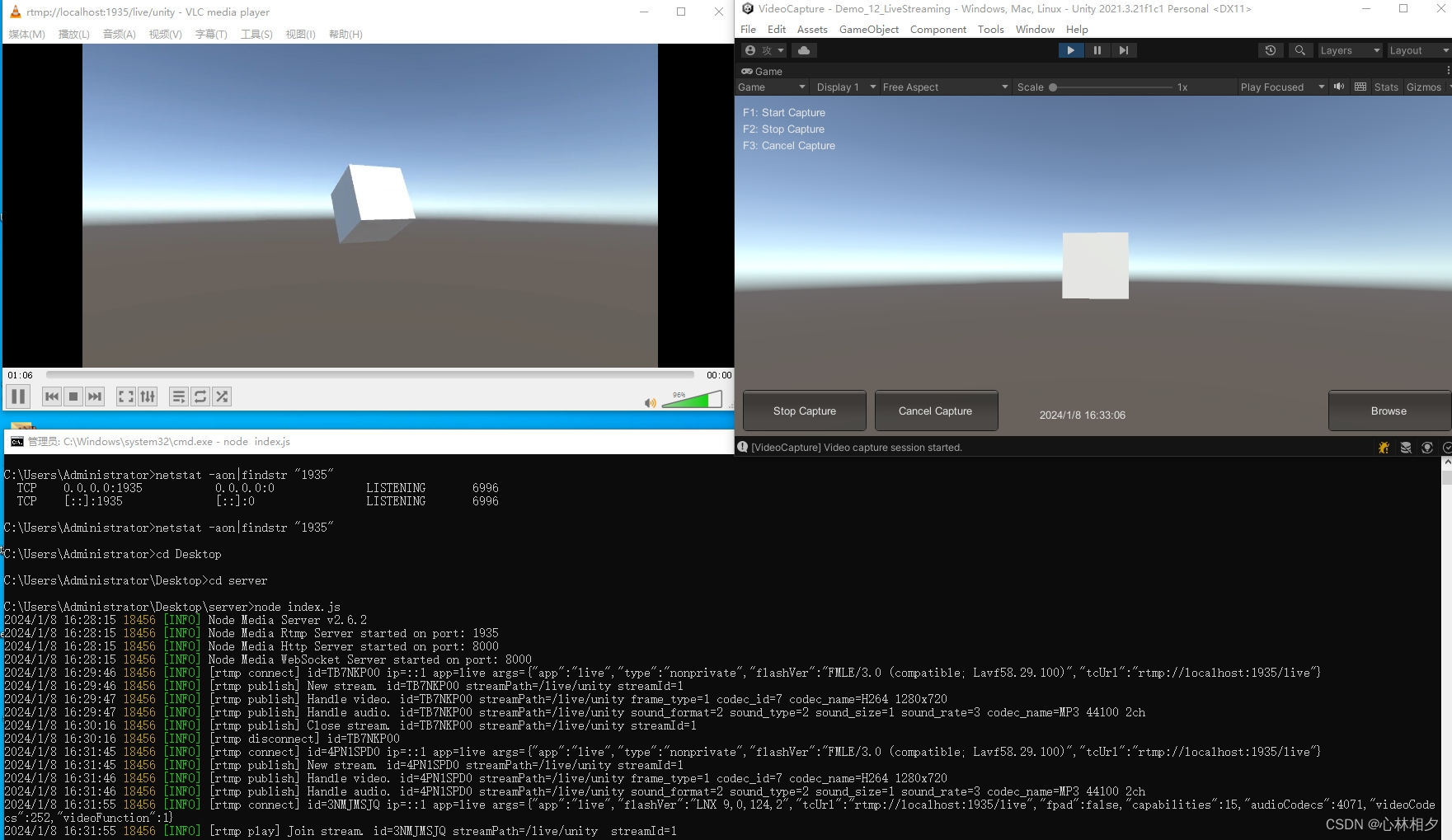
Unity3d 实现直播功能(无需sdk接入)
Unity3d 实现直播功能 需要插件 :VideoCapture 插件地址(免费的就行) 原理:客户端通过 VideoCapture 插件实现推流nodejs视频流转服务进行转发,播放器实现rtmp拉流 废话不多说,直接上 CaptureSource我选择的是屏幕录制,也可以是其他源 CaptureType选择LIVE–直播形式 LiveSt…...
计算机缺失msvcr100.dll如何修复?分享五种实测靠谱的方法
在计算机系统的日常运行与维护过程中,我们可能会遇到一种特定的故障场景,即系统中关键性动态链接库文件msvcr100.dll的丢失。msvcr100.dll是Microsoft Visual C Redistributable Package的一部分,对于许多基于Windows的应用程序来说ÿ…...
面试宝典进阶之redis缓存面试题
R1、【初级】Redis常用的数据类型有哪些? (1)String(字符串) (2)Hash(哈希) (3)List(列表) (4)Se…...

调试(c语言)
前言: 我们在写程序的时候可能多多少少都会出现一些bug,使我们的程序不能正常运行,所以为了更快更好的找到并修复bug,使这些问题迎刃而解,学习好如何调试代码是每个学习编程的人所必备的技能。 1. 什么是bug…...
opencv-4.8.0编译及使用
1 编译 opencv的编译总体来说比较简单,但必须记住一点:opencv的版本必须和opencv_contrib的版本保持一致。例如opencv使用4.8.0,opencv_contrib也必须使用4.8.0。 进入opencv和opencv_contrib的github页面后,默认看到的是git分支&…...

Jmeter 性能-监控服务器
Jmeter监控Linux需要三个文件 JMeterPlugins-Extras.jar (包:JMeterPlugins-Extras-1.4.0.zip) JMeterPlugins-Standard.jar (包:JMeterPlugins-Standard-1.4.0.zip) ServerAgent-2.2.3.zip 1、Jemter 安装插件 在插件管理中心的搜索Servers Perform…...
Excel学习
文章目录 学习链接Excel1. Excel的两种形式2. 常见excel操作工具3.POI1. POI的概述2. POI的应用场景3. 使用1.使用POI创建excel2.创建单元格写入内容3.单元格样式处理4.插入图片5.读取excel并解析图解POI 4. 基于模板输出POI报表5. 自定义POI导出工具类ExcelAttributeExcelExpo…...

【技能---labelme软件的安装及其使用--ubuntu】
文章目录 概要Labelme 是什么?Labelme 能干啥? Ubuntu20.04安装Labelme1.Anaconda的安装2.Labelme的安装3.Labelme的使用 概要 图像检测需要自己的数据集,为此需要对一些数据进行数据标注,这里提供了一种图像的常用标注工具——la…...

回归预测 | Matlab实现SSA-CNN-LSTM-Attention麻雀优化卷积长短期记忆神经网络注意力机制多变量回归预测(SE注意力机制)
回归预测 | Matlab实现SSA-CNN-LSTM-Attention麻雀优化卷积长短期记忆神经网络注意力机制多变量回归预测(SE注意力机制) 目录 回归预测 | Matlab实现SSA-CNN-LSTM-Attention麻雀优化卷积长短期记忆神经网络注意力机制多变量回归预测(SE注意力…...

css垂直水平居中的几种实现方式
垂直水平居中的几种实现方式 一、固定宽高: 1、定位 margin-top margin-left .box-container{position: relative;width: 300px;height: 300px;}.box-container .box {width: 200px; height: 100px;position: absolute; left: 50%; top: 50%;margin-top: -50px;…...

OpenHarmony之hdc
OpenHarmony之hdc 简介 hdc(OpenHarmony Device Connector)是 OpenHarmony 为开发人员提供的用于调试的命令行工具,通过该工具可以在Windows/Linux/MacOS等系统上与开发机或者模拟器进行交互。 类似于Android的adb,和adb类似&a…...
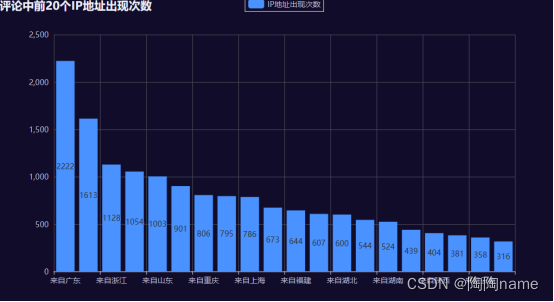
【爬虫实战】-爬取微博之夜盛典评论,爬取了1.7w条数据
前言: TaoTao之前在前几期推文中发布了一个篇weibo评论的爬虫。主要就是采集评论区的数据,包括评论、评论者ip、评论id、评论者等一些信息。然后有很多的小伙伴对这个代码很感兴趣。TaoTao也都给代码开源了。由于比较匆忙,所以没来得及去讲这…...

CST2024的License服务成功启动,仍报错——“The desired daemon is down...”,适用于任何版本!基础设置遗漏!
CST2024的License服务成功启动,仍报错——“The desired daemon is down…”,适用于任何版本!基础设置遗漏! CST2024的License服务成功启动后报错 若不能成功启动License服务,有可能是你的计算机名称带中文ÿ…...

matlab中any()函数用法
一、帮助文档中的介绍 B any(A) 沿着大小不等于 1 的数组 A 的第一维测试所有元素为非零数字还是逻辑值 1 (true)。实际上,any 是逻辑 OR 运算符的原生扩展。 二、解读 分两步走: ①确定维度;②确定运算规则 以下面二维数组为例 >>…...
Apache ECharts | 一个数据可视化图表库
文章目录 1、简介1.1、主要特点1.2、使用场景 2、安装方式一:从下载的源代码或编译产物安装方法二:从 npm 安装方法三:⭐定制安装echarts.js 3、使用 官网: 英语:https://echarts.apache.org/en/index.html 中文&a…...
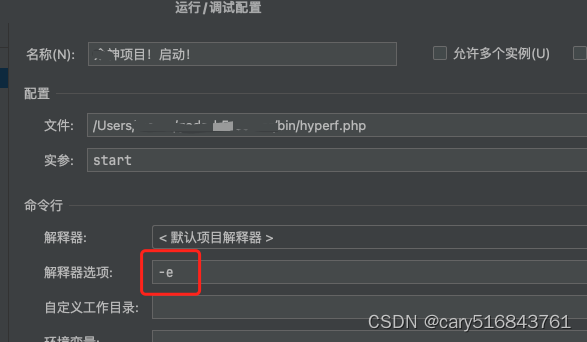
m1 + swoole(hyperf) + yasd + phpstorm 安装和debug
参考文档 Mac M1安装报错 checking for boost... configure: error: lib boost not found. Try: install boost library Issue #89 swoole/yasd GitHub 1.安装boost库 brew install boostbrew link boost 2.下载yasd git clone https://github.com/swoole/yasd.git 3.编…...
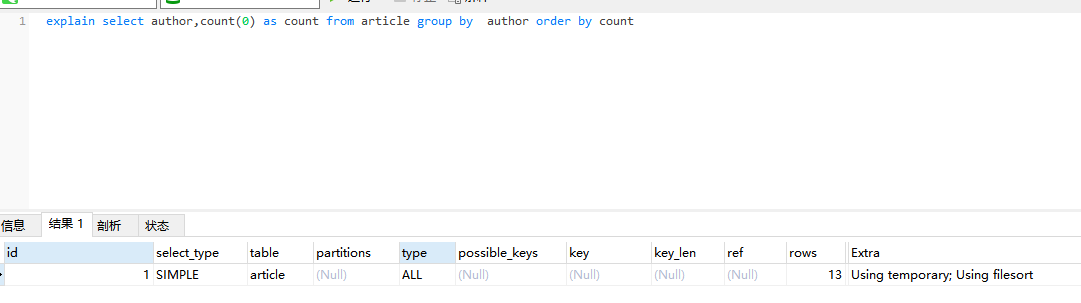
group by 查询慢的话,如何优化?
1、说明 根据一定的规则,进行分组。 group by可能会慢在哪里?因为它既用到临时表,又默认用到排序。有时候还可能用到磁盘临时表。 如果执行过程中,会发现内存临时表大小到达了上限(控制这个上限的参数就是tmp_table…...

【重学C语言】一、C语言简介
【重学C语言】一、C语言简介 什么是编程语言?编程语言 C语言发展史C语言标准变迁开发软件CLion安装步骤 VIsual Studio安装步骤 Clion 和 VS2022 绑定 电脑常识 什么是编程语言? 人类语言:语言就是人类进行沟通交流的表达方式,应…...

MFC内存泄露
1、泄露代码示例 void X::SetApplicationBtn() {CMFCRibbonApplicationButton* pBtn GetApplicationButton();// 获取 Ribbon Bar 指针// 创建自定义按钮CCustomRibbonAppButton* pCustomButton new CCustomRibbonAppButton();pCustomButton->SetImage(IDB_BITMAP_Jdp26)…...

页面渲染流程与性能优化
页面渲染流程与性能优化详解(完整版) 一、现代浏览器渲染流程(详细说明) 1. 构建DOM树 浏览器接收到HTML文档后,会逐步解析并构建DOM(Document Object Model)树。具体过程如下: (…...

【学习笔记】深入理解Java虚拟机学习笔记——第4章 虚拟机性能监控,故障处理工具
第2章 虚拟机性能监控,故障处理工具 4.1 概述 略 4.2 基础故障处理工具 4.2.1 jps:虚拟机进程状况工具 命令:jps [options] [hostid] 功能:本地虚拟机进程显示进程ID(与ps相同),可同时显示主类&#x…...

三分算法与DeepSeek辅助证明是单峰函数
前置 单峰函数有唯一的最大值,最大值左侧的数值严格单调递增,最大值右侧的数值严格单调递减。 单谷函数有唯一的最小值,最小值左侧的数值严格单调递减,最小值右侧的数值严格单调递增。 三分的本质 三分和二分一样都是通过不断缩…...

PHP 8.5 即将发布:管道操作符、强力调试
前不久,PHP宣布了即将在 2025 年 11 月 20 日 正式发布的 PHP 8.5!作为 PHP 语言的又一次重要迭代,PHP 8.5 承诺带来一系列旨在提升代码可读性、健壮性以及开发者效率的改进。而更令人兴奋的是,借助强大的本地开发环境 ServBay&am…...

【从零开始学习JVM | 第四篇】类加载器和双亲委派机制(高频面试题)
前言: 双亲委派机制对于面试这块来说非常重要,在实际开发中也是经常遇见需要打破双亲委派的需求,今天我们一起来探索一下什么是双亲委派机制,在此之前我们先介绍一下类的加载器。 目录 编辑 前言: 类加载器 1. …...

Kubernetes 网络模型深度解析:Pod IP 与 Service 的负载均衡机制,Service到底是什么?
Pod IP 的本质与特性 Pod IP 的定位 纯端点地址:Pod IP 是分配给 Pod 网络命名空间的真实 IP 地址(如 10.244.1.2)无特殊名称:在 Kubernetes 中,它通常被称为 “Pod IP” 或 “容器 IP”生命周期:与 Pod …...

密码学基础——SM4算法
博客主页:christine-rr-CSDN博客 专栏主页:密码学 📌 【今日更新】📌 对称密码算法——SM4 目录 一、国密SM系列算法概述 二、SM4算法 2.1算法背景 2.2算法特点 2.3 基本部件 2.3.1 S盒 2.3.2 非线性变换 编辑…...

多元隐函数 偏导公式
我们来推导隐函数 z z ( x , y ) z z(x, y) zz(x,y) 的偏导公式,给定一个隐函数关系: F ( x , y , z ( x , y ) ) 0 F(x, y, z(x, y)) 0 F(x,y,z(x,y))0 🧠 目标: 求 ∂ z ∂ x \frac{\partial z}{\partial x} ∂x∂z、 …...

leetcode73-矩阵置零
leetcode 73 思路 记录 0 元素的位置:遍历整个矩阵,找出所有值为 0 的元素,并将它们的坐标记录在数组zeroPosition中置零操作:遍历记录的所有 0 元素位置,将每个位置对应的行和列的所有元素置为 0 具体步骤 初始化…...
