鸿蒙开发现在就业前景怎样?
随着科技的不断进步,鸿蒙系统逐渐崭露头角,成为智能设备领域的一颗新星。作为华为自主研发的操作系统,鸿蒙系统拥有着广阔的市场前景和就业机会。那么,鸿蒙开发的就业前景究竟怎样呢?
一、市场需求持续增长
随着鸿蒙系统的不断推广和应用,市场对鸿蒙开发人才的需求也在持续增长。从智能手机、智能家居到智能交通、智慧城市等领域,鸿蒙系统的应用场景越来越广泛,需要更多的开发人才来满足市场需求。

二、技术要求高
鸿蒙开发需要具备较高的技术水平,要求开发者熟练掌握C/C++、Java等编程语言,同时还需要熟悉操作系统原理、分布式系统架构、云计算和人工智能等方面的知识。因此,对于具备相关技能和经验的开发者来说,鸿蒙开发具有较高的技术门槛。

三、就业机会多样化
随着鸿蒙系统的不断推广和应用,就业机会也在不断增加。除了华为自身需要大量的鸿蒙开发人才外,许多其他企业也开始涉足鸿蒙系统开发领域,需要大量的专业人才。因此,鸿蒙开发的就业机会呈现出多样化的特点。
四、薪资水平较高
由于鸿蒙开发需要较高的技术水平和丰富的经验,因此薪资水平也相对较高。根据市场调查数据显示,具备一定经验的鸿蒙开发工程师的年薪普遍在几十万到数百万不等。

五、未来发展前景广阔
随着5G、物联网、人工智能等技术的不断发展,智能设备的应用场景将会越来越广泛,鸿蒙系统作为智能设备领域的重要操作系统之一,未来发展前景广阔。因此,对于具备相关技能和经验的开发者来说,鸿蒙开发具有较大的发展潜力。
鸿蒙开发的就业前景呈现出市场需求持续增长、技术要求高、就业机会多样化、薪资水平较高以及未来发展前景广阔等特点。对于具备相关技能和经验的开发者来说,选择从事鸿蒙开发领域将是一个具有较大发展潜力的职业选择。
码牛课堂推出鸿蒙路线图,助你笑傲职场
①全方位,更合理的学习路径
路线图包括ArkTS基础语法、鸿蒙应用APP开发、鸿蒙能力集APP开发、次开发多端部署开发、物联网开发等九大模块,六大实战项目贯穿始终,由浅入深,层层递进,深入理解鸿蒙开发原理!
②多层次,更多的鸿蒙原生应用
路线图将包含完全基于鸿蒙内核开发的应用,比如一次开发多端部署、自由流转、元服务、端云一体化等,多方位的学习内容让学生能够高效掌握鸿蒙开发,少走弯路,真正理解并应用鸿蒙的核心技术和理念。
③实战化,更贴合企业需求的技术点
学习路线图中的每一个技术点都能够紧贴企业需求,经过多次真实实践,每一个知识点、每一个项目,都是码牛课堂鸿蒙研发团队精心打磨和深度解析的成果,注重对学生的细致教学,每一步都确保学生能够真正理解和掌握。

路线图适合人群
- IT开发人员:想要拓展职业边界,享受新技术溢价红利;
- 零基础小白:鸿蒙爱好者,希望从0到1学习,增加一项技能。
为了能让大家更好的学习鸿蒙 (OpenHarmony) 开发技术,这边特意整理了《鸿蒙 (OpenHarmony)开发学习手册》(共计890页),希望对大家有所帮助:https://qr21.cn/FV7h05
《鸿蒙 (OpenHarmony)开发学习手册》
入门必看:https://qr21.cn/FV7h05
- 应用开发导读(ArkTS)
- ……

HarmonyOS 概念:https://qr21.cn/FV7h05
- 系统定义
- 技术架构
- 技术特性
- 系统安全

如何快速入门?:https://qr21.cn/FV7h05
- 基本概念
- 构建第一个ArkTS应用
- 构建第一个JS应用
- ……

开发基础知识:https://qr21.cn/FV7h05
- 应用基础知识
- 配置文件
- 应用数据管理
- 应用安全管理
- 应用隐私保护
- 三方应用调用管控机制
- 资源分类与访问
- 学习ArkTS语言
- ……

基于ArkTS 开发:https://qr21.cn/FV7h05
1.Ability开发
2.UI开发
3.公共事件与通知
4.窗口管理
5.媒体
6.安全
7.网络与链接
8.电话服务
9.数据管理
10.后台任务(Background Task)管理
11.设备管理
12.设备使用信息统计
13.DFX
14.国际化开发
15.折叠屏系列
16.……

相关文章:

鸿蒙开发现在就业前景怎样?
随着科技的不断进步,鸿蒙系统逐渐崭露头角,成为智能设备领域的一颗新星。作为华为自主研发的操作系统,鸿蒙系统拥有着广阔的市场前景和就业机会。那么,鸿蒙开发的就业前景究竟怎样呢? 一、市场需求持续增长 随着鸿蒙…...
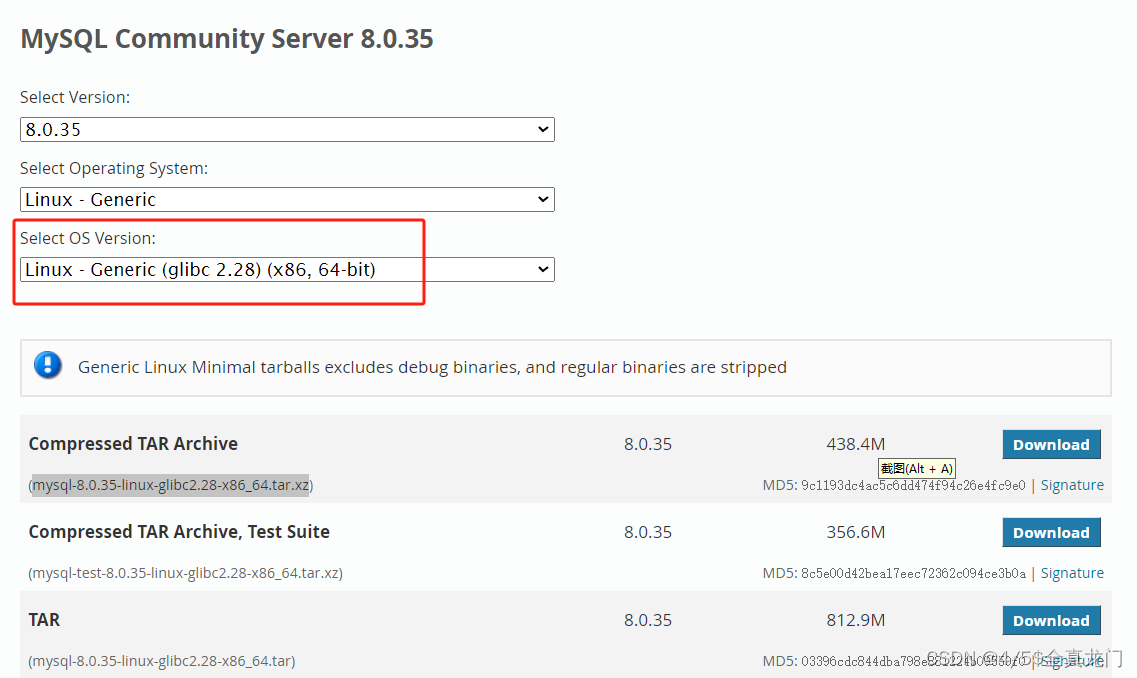
试用统信服务器操作系统UOS 20
作者:田逸(formyz) 试用统信Linux操作系统UOS,想了解一下用已有的Linux经验能否轻松驾驭它。以便在某些场景下,可以多一种选择。本次试验在Proxmox VE 8(以下简称PVE 8)平台下进行,采…...
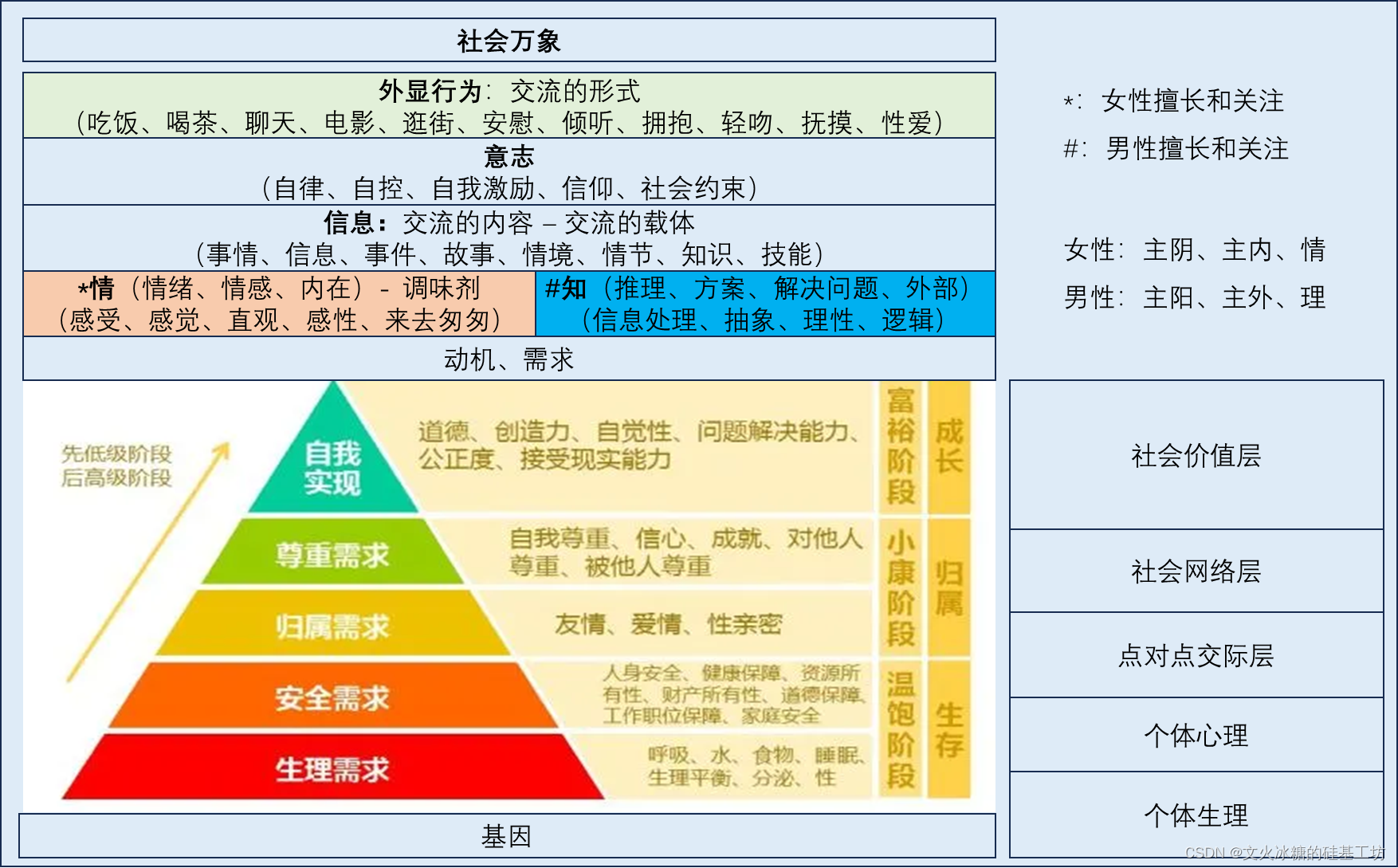
[情商-11]:人际交流的心理架构与需求层次模型
目录 前言: 一、心理架构 1.1 个体生理层 1.2 个体心理层 1.3 点对点人际交流层 1.4 社会网络层 1.5 社会价值层 二、人的需求层次模型 2.1 需求(欲望)层次模型 2.2 基因与人需求之间的关系 2.3 个体生理需求 2.4 个体的心理需求…...

【.NET Core】Lazy<T> 实现延迟加载详解
【.NET Core】Lazy 实现延迟加载详解 文章目录 【.NET Core】Lazy<T> 实现延迟加载详解一、概述二、Lazy<T>是什么三、Lazy基本用法3.1 构造时使用默认的初始化方式3.2 构造时使用指定的委托初始化 四、Lazy.Value使用五、Lazy扩展用法5.1 实现延迟属性5.2 Lazy实现…...
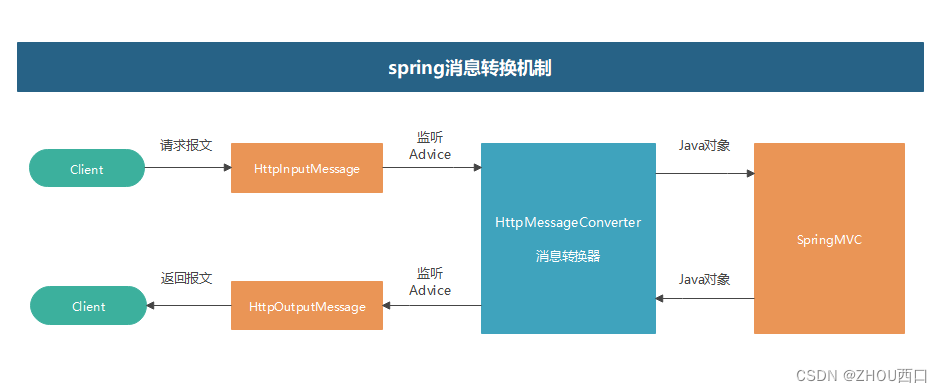
坑记(HttpInputMessage)
一、背景知识 public interface HttpInputMessage extends HttpMessage Represents an HTTP input message, consisting of headers and a readable body.Typically implemented by an HTTP request on the server-side, or a response on the client-side.Since: 3.0 Author:…...

day04打卡
day04打卡 面试题 02.07. 链表相交 时间复杂度:O(N),空间复杂度:O(1) 第一想法:求出两个链表长度,走差距步,再遍历找有没有相交 /*** Definition for singly-linked list.* struct ListNode {* int…...

语义分割miou指标计算详解
文章目录 1. 语义分割的评价指标2. 混淆矩阵计算2.1 np.bincount的使用2.2 混淆矩阵计算 3. 语义分割指标计算3.1 IOU计算方式1(推荐)方式2 3.2 Precision 计算3.3 总体的Accuracy计算3.4 Recall 计算3.5 MIOU计算 参考 MIoU全称为Mean Intersection over Union,平均…...
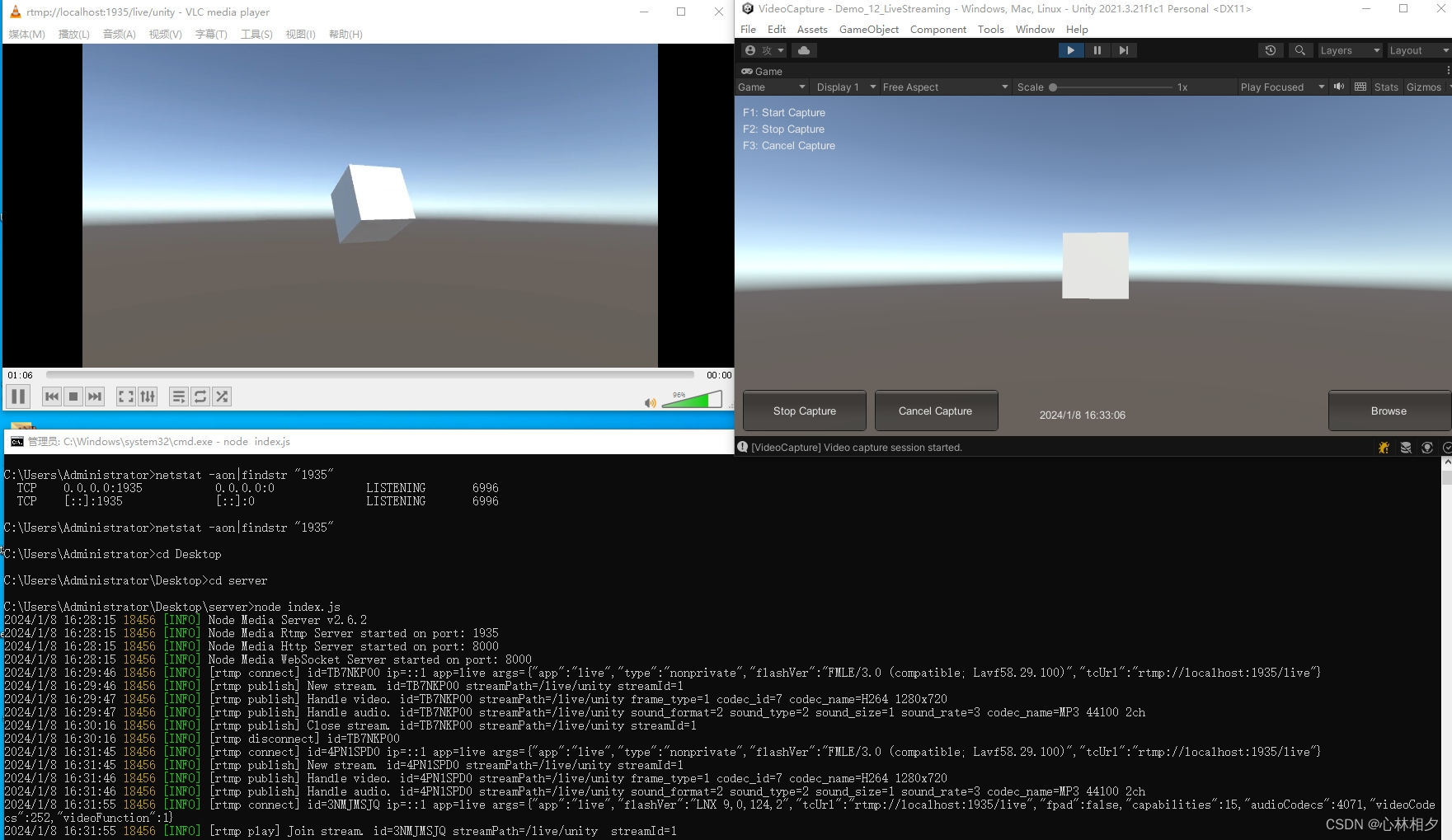
Unity3d 实现直播功能(无需sdk接入)
Unity3d 实现直播功能 需要插件 :VideoCapture 插件地址(免费的就行) 原理:客户端通过 VideoCapture 插件实现推流nodejs视频流转服务进行转发,播放器实现rtmp拉流 废话不多说,直接上 CaptureSource我选择的是屏幕录制,也可以是其他源 CaptureType选择LIVE–直播形式 LiveSt…...
计算机缺失msvcr100.dll如何修复?分享五种实测靠谱的方法
在计算机系统的日常运行与维护过程中,我们可能会遇到一种特定的故障场景,即系统中关键性动态链接库文件msvcr100.dll的丢失。msvcr100.dll是Microsoft Visual C Redistributable Package的一部分,对于许多基于Windows的应用程序来说ÿ…...
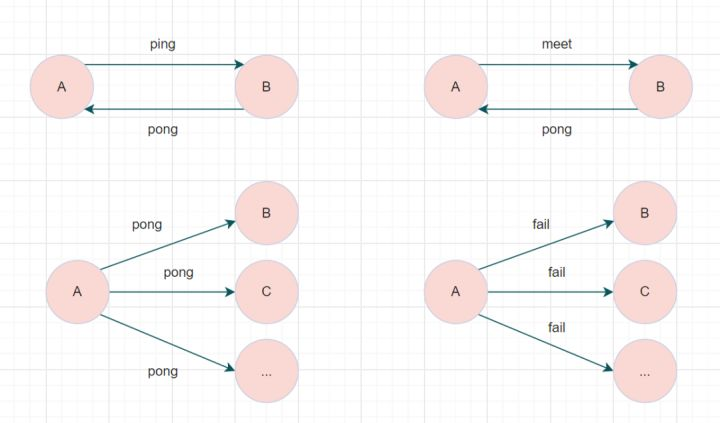
面试宝典进阶之redis缓存面试题
R1、【初级】Redis常用的数据类型有哪些? (1)String(字符串) (2)Hash(哈希) (3)List(列表) (4)Se…...

调试(c语言)
前言: 我们在写程序的时候可能多多少少都会出现一些bug,使我们的程序不能正常运行,所以为了更快更好的找到并修复bug,使这些问题迎刃而解,学习好如何调试代码是每个学习编程的人所必备的技能。 1. 什么是bug…...
opencv-4.8.0编译及使用
1 编译 opencv的编译总体来说比较简单,但必须记住一点:opencv的版本必须和opencv_contrib的版本保持一致。例如opencv使用4.8.0,opencv_contrib也必须使用4.8.0。 进入opencv和opencv_contrib的github页面后,默认看到的是git分支&…...

Jmeter 性能-监控服务器
Jmeter监控Linux需要三个文件 JMeterPlugins-Extras.jar (包:JMeterPlugins-Extras-1.4.0.zip) JMeterPlugins-Standard.jar (包:JMeterPlugins-Standard-1.4.0.zip) ServerAgent-2.2.3.zip 1、Jemter 安装插件 在插件管理中心的搜索Servers Perform…...
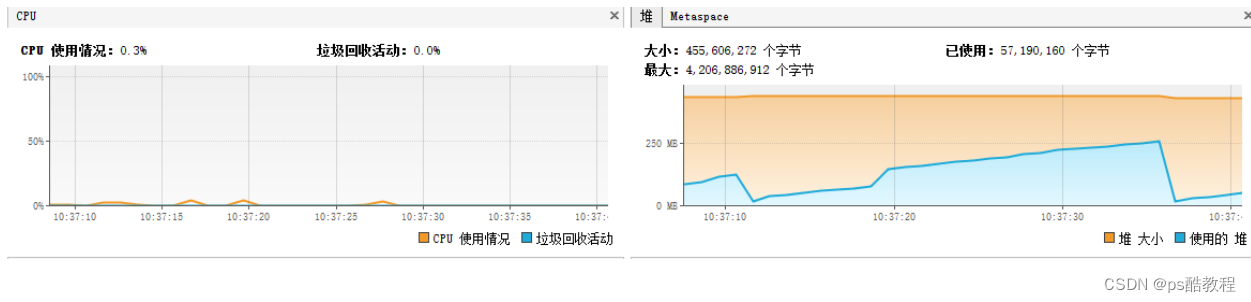
Excel学习
文章目录 学习链接Excel1. Excel的两种形式2. 常见excel操作工具3.POI1. POI的概述2. POI的应用场景3. 使用1.使用POI创建excel2.创建单元格写入内容3.单元格样式处理4.插入图片5.读取excel并解析图解POI 4. 基于模板输出POI报表5. 自定义POI导出工具类ExcelAttributeExcelExpo…...

【技能---labelme软件的安装及其使用--ubuntu】
文章目录 概要Labelme 是什么?Labelme 能干啥? Ubuntu20.04安装Labelme1.Anaconda的安装2.Labelme的安装3.Labelme的使用 概要 图像检测需要自己的数据集,为此需要对一些数据进行数据标注,这里提供了一种图像的常用标注工具——la…...

回归预测 | Matlab实现SSA-CNN-LSTM-Attention麻雀优化卷积长短期记忆神经网络注意力机制多变量回归预测(SE注意力机制)
回归预测 | Matlab实现SSA-CNN-LSTM-Attention麻雀优化卷积长短期记忆神经网络注意力机制多变量回归预测(SE注意力机制) 目录 回归预测 | Matlab实现SSA-CNN-LSTM-Attention麻雀优化卷积长短期记忆神经网络注意力机制多变量回归预测(SE注意力…...

css垂直水平居中的几种实现方式
垂直水平居中的几种实现方式 一、固定宽高: 1、定位 margin-top margin-left .box-container{position: relative;width: 300px;height: 300px;}.box-container .box {width: 200px; height: 100px;position: absolute; left: 50%; top: 50%;margin-top: -50px;…...

OpenHarmony之hdc
OpenHarmony之hdc 简介 hdc(OpenHarmony Device Connector)是 OpenHarmony 为开发人员提供的用于调试的命令行工具,通过该工具可以在Windows/Linux/MacOS等系统上与开发机或者模拟器进行交互。 类似于Android的adb,和adb类似&a…...
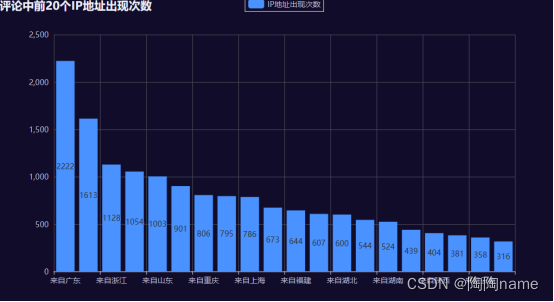
【爬虫实战】-爬取微博之夜盛典评论,爬取了1.7w条数据
前言: TaoTao之前在前几期推文中发布了一个篇weibo评论的爬虫。主要就是采集评论区的数据,包括评论、评论者ip、评论id、评论者等一些信息。然后有很多的小伙伴对这个代码很感兴趣。TaoTao也都给代码开源了。由于比较匆忙,所以没来得及去讲这…...

CST2024的License服务成功启动,仍报错——“The desired daemon is down...”,适用于任何版本!基础设置遗漏!
CST2024的License服务成功启动,仍报错——“The desired daemon is down…”,适用于任何版本!基础设置遗漏! CST2024的License服务成功启动后报错 若不能成功启动License服务,有可能是你的计算机名称带中文ÿ…...

树莓派超全系列教程文档--(61)树莓派摄像头高级使用方法
树莓派摄像头高级使用方法 配置通过调谐文件来调整相机行为 使用多个摄像头安装 libcam 和 rpicam-apps依赖关系开发包 文章来源: http://raspberry.dns8844.cn/documentation 原文网址 配置 大多数用例自动工作,无需更改相机配置。但是,一…...

SCAU期末笔记 - 数据分析与数据挖掘题库解析
这门怎么题库答案不全啊日 来简单学一下子来 一、选择题(可多选) 将原始数据进行集成、变换、维度规约、数值规约是在以下哪个步骤的任务?(C) A. 频繁模式挖掘 B.分类和预测 C.数据预处理 D.数据流挖掘 A. 频繁模式挖掘:专注于发现数据中…...
指令的指南)
在Ubuntu中设置开机自动运行(sudo)指令的指南
在Ubuntu系统中,有时需要在系统启动时自动执行某些命令,特别是需要 sudo权限的指令。为了实现这一功能,可以使用多种方法,包括编写Systemd服务、配置 rc.local文件或使用 cron任务计划。本文将详细介绍这些方法,并提供…...

Spring Boot面试题精选汇总
🤟致敬读者 🟩感谢阅读🟦笑口常开🟪生日快乐⬛早点睡觉 📘博主相关 🟧博主信息🟨博客首页🟫专栏推荐🟥活动信息 文章目录 Spring Boot面试题精选汇总⚙️ **一、核心概…...
)
Angular微前端架构:Module Federation + ngx-build-plus (Webpack)
以下是一个完整的 Angular 微前端示例,其中使用的是 Module Federation 和 npx-build-plus 实现了主应用(Shell)与子应用(Remote)的集成。 🛠️ 项目结构 angular-mf/ ├── shell-app/ # 主应用&…...

08. C#入门系列【类的基本概念】:开启编程世界的奇妙冒险
C#入门系列【类的基本概念】:开启编程世界的奇妙冒险 嘿,各位编程小白探险家!欢迎来到 C# 的奇幻大陆!今天咱们要深入探索这片大陆上至关重要的 “建筑”—— 类!别害怕,跟着我,保准让你轻松搞…...

多模态图像修复系统:基于深度学习的图片修复实现
多模态图像修复系统:基于深度学习的图片修复实现 1. 系统概述 本系统使用多模态大模型(Stable Diffusion Inpainting)实现图像修复功能,结合文本描述和图片输入,对指定区域进行内容修复。系统包含完整的数据处理、模型训练、推理部署流程。 import torch import numpy …...

Vite中定义@软链接
在webpack中可以直接通过符号表示src路径,但是vite中默认不可以。 如何实现: vite中提供了resolve.alias:通过别名在指向一个具体的路径 在vite.config.js中 import { join } from pathexport default defineConfig({plugins: [vue()],//…...

DeepSeek源码深度解析 × 华为仓颉语言编程精粹——从MoE架构到全场景开发生态
前言 在人工智能技术飞速发展的今天,深度学习与大模型技术已成为推动行业变革的核心驱动力,而高效、灵活的开发工具与编程语言则为技术创新提供了重要支撑。本书以两大前沿技术领域为核心,系统性地呈现了两部深度技术著作的精华:…...

拟合问题处理
在机器学习中,核心任务通常围绕模型训练和性能提升展开,但你提到的 “优化训练数据解决过拟合” 和 “提升泛化性能解决欠拟合” 需要结合更准确的概念进行梳理。以下是对机器学习核心任务的系统复习和修正: 一、机器学习的核心任务框架 机…...
