每日一题——LeetCode1128.等价多米诺骨牌对的数量

先尝试暴力解法:
var numEquivDominoPairs = function(dominoes) {var count=0for(let i=0;i<dominoes.length-1;i++){for(let j=i+1;j<dominoes.length;j++){if((dominoes[i][0]==dominoes[j][0] && dominoes[i][1]==dominoes[j][1]) || (dominoes[i][0]==dominoes[j][1] && dominoes[i][1]==dominoes[j][0])){count++}}}return count
};可惜时间超限:

直接参考官方解法,太巧妙了:
不妨直接让每一个二元对都变为指定的格式,即第一维必须不大于第二维。这样两个二元对「等价」当且仅当两个二元对完全相同。
注意到二元对中的元素均不大于 9,因此我们可以将每一个二元对拼接成一个两位的正整数,即 (x,y)→10x+y(x, y) 。这样就无需使用哈希表统计元素数量,而直接使用长度为 100的数组即可。
作者:力扣官方题解
链接:1128 官方题解
var numEquivDominoPairs = function(dominoes) {const num = new Array(100).fill(0);let ret = 0;for (const domino of dominoes) {const val = domino[0] < domino[1] ? domino[0] * 10 + domino[1] : domino[1] * 10 + domino[0];ret += num[val];num[val]++;}return ret;
};
消耗时间和内存情况:

相关文章:

每日一题——LeetCode1128.等价多米诺骨牌对的数量
先尝试暴力解法: var numEquivDominoPairs function(dominoes) {var count0for(let i0;i<dominoes.length-1;i){for(let ji1;j<dominoes.length;j){if((dominoes[i][0]dominoes[j][0] && dominoes[i][1]dominoes[j][1]) || (dominoes[i][0]dominoes…...
关联规则分析(Apriori算法2
目录 1.核心术语:2.强关联规则:小结: 1.核心术语: 支持度(Support):指项集出现的频繁程度(相当于项集出现的概率) 最小支持度有绝对值和占比两种表示方式 置信度&#…...
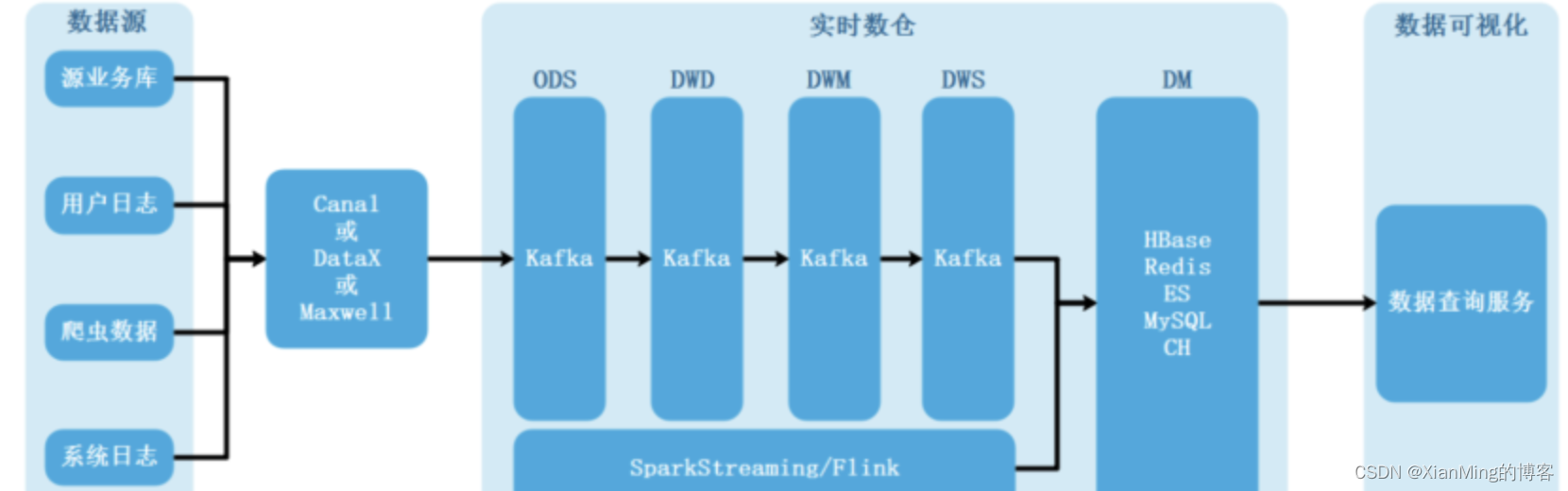
数据仓库(2)-认识数仓
1、数据仓库是什么 数据仓库 ,由数据仓库之父比尔恩门(Bill Inmon)于1990年提出,主要功能仍是将组织透过资讯系统之联机事务处理(OLTP)经年累月所累积的大量资料,透过数据仓库理论所特有的资料储存架构,做…...

C#编程-实现委托
实现委托 委托是可以存储对方法的引用的对象。在C#中,委托允许您动态地改变类中方法的引用。 考虑咖啡售货机的示例,它配置不同口味的咖啡,例如卡布奇诺咖啡和黑咖啡。在选择所需口味的咖啡时,售货机决定混合各种成分,例如奶粉、咖啡粉、热水、卡布奇诺咖啡粉。所有的材…...
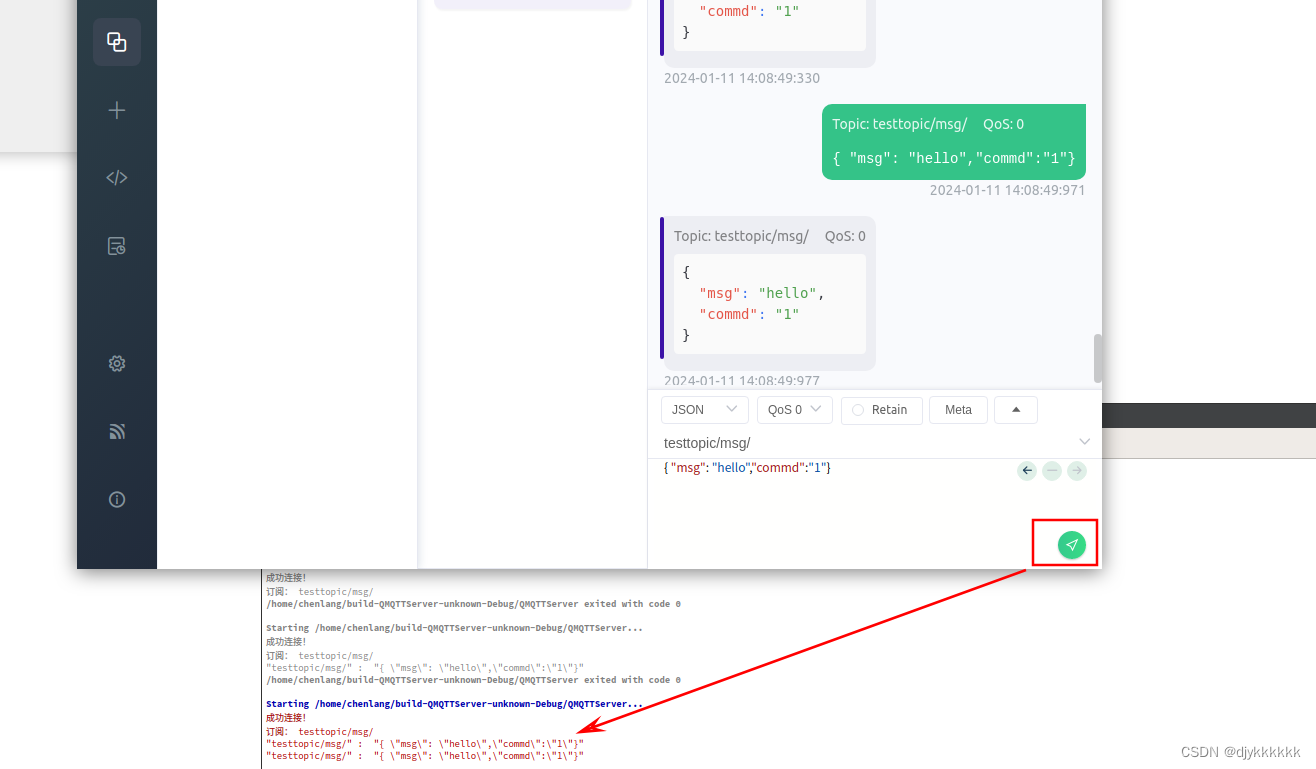
Ubuntu18.04 Qt 实现MQTT
什么是MQTT? 作用是什么(适用场景)? 与其他通讯协议相比,优缺点在那里? 一.安装 MQTT 服务器 使用 EMQ X(开源且可视化管理) 下载 EMQX 下载的是 emqx-5.0.26-ubuntu18.04-…...

【软件测试】学习笔记-不同视角的软件性能与性能指标
本篇文章探讨新的测试主题:性能测试,因为性能测试的专业性很强,所以我会以从0到1的入门者视角,系统性地阐述性能测试的方法以及应用领域,用实例去诠释各种性能指标。 本篇文章站在全局的视角,帮你梳理软件性…...
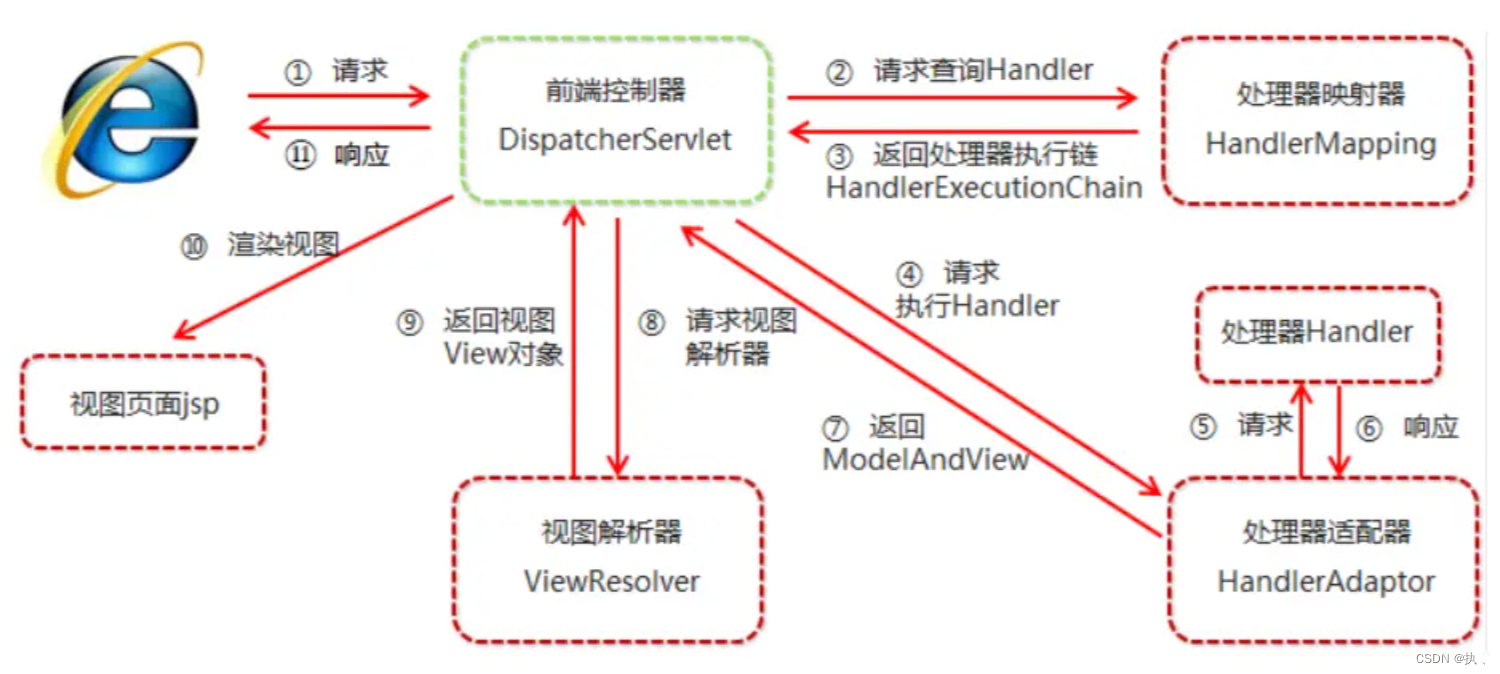
Spring MVC组件
1.DispatcherServlet前端控制器 用户请求到达前端控制器,它就相当于mvc模式中的c,dispatcherServlet 是整个流程控制的中心,由它调用其它组件处理用户的请求,dispatcherServlet 的存在降低了组件之间的耦合性。 2.HandlerMappin…...

vue文件在<template>中使用多个<el-main>报错(已解决)
目录 1.原理 2. 根据你的需求,自定义每个 组件的内容。你可以在 标签内部插入文本、其他组件、样式等。 3. 根据需要添加样式或其他属性到每个 组件。你可以使用 class、style 或其他属性来自定义每个组件的外观和行为。 4.一个可以运行的总代码如下 5.我的一…...
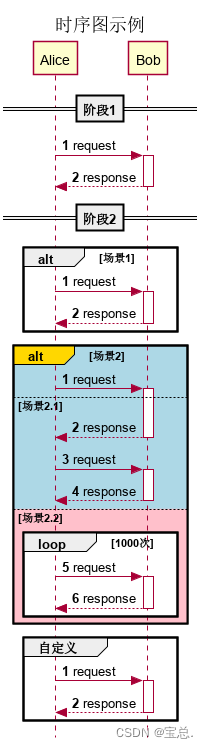
【PlantUML】- 时序图
写在前面 本篇文章,我们来介绍一下PlantUML的时序图。这个相对类图来讲,比较简单,也不需要布局。读完文章,相信你就能实际操作了。 目录 写在前面一、基本概念二、具体步骤1.环境说明2.元素3.语法4.示例 三、参考资料写在后面系列…...

openai自定义API操作 API (openai.custom):OpenAI API 实现电商平台的智能库存管理
在电商行业中,库存管理是至关重要的环节之一。一个高效的库存管理系统可以确保商品的正常供应,避免缺货或积压现象,从而提高销售效率和客户满意度。然而,传统的库存管理方式往往存在一些问题,如数据不准确、响应不及时…...
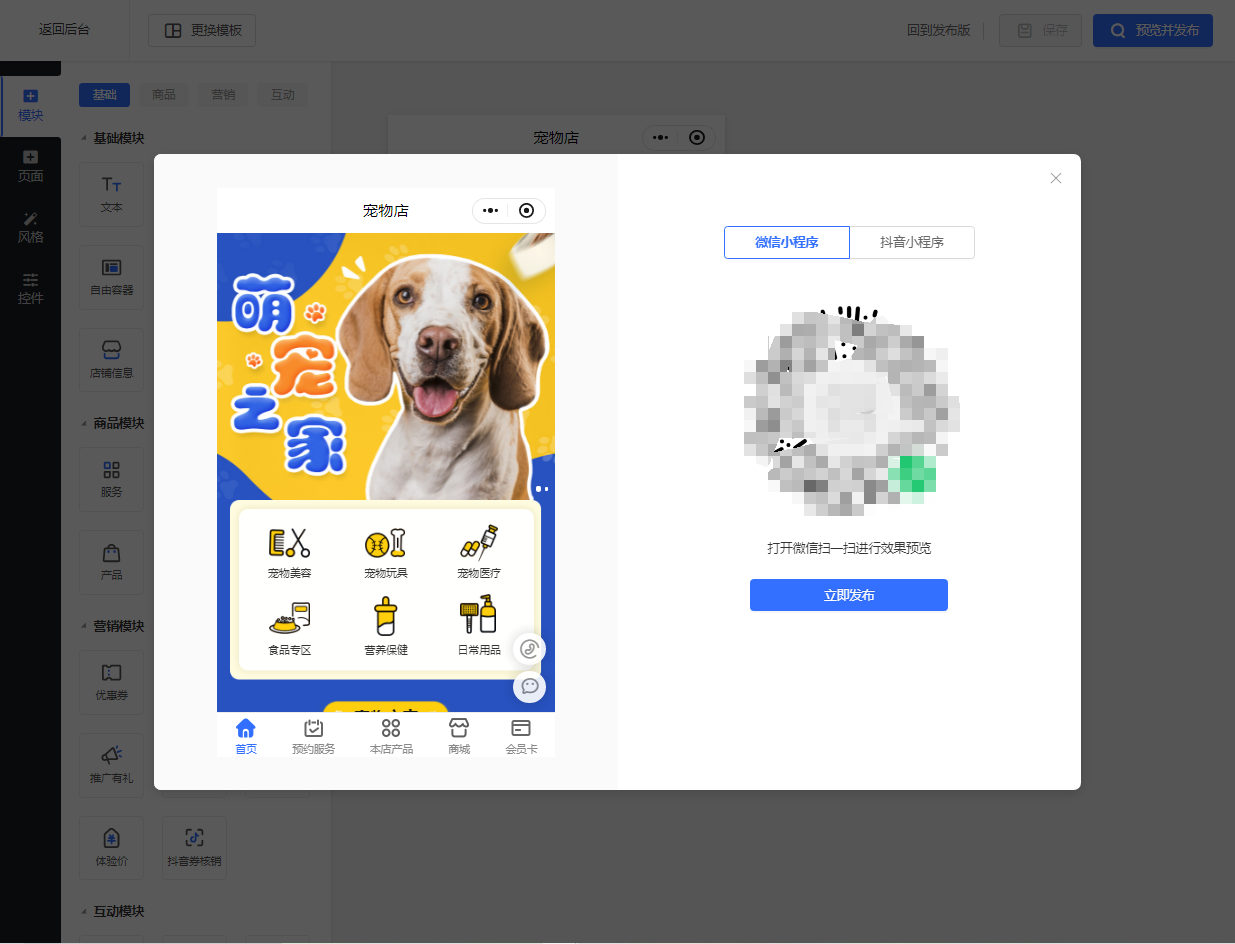
宠物服务新篇章:预约小程序带来的变革
随着科技的进步和互联网的普及,小程序已经成为了一种非常受欢迎的应用形式。对于宠物门店来说,开发一个预约小程序可以大大提高客户体验和管理效率。下面是一份宠物门店预约小程序的开发指南。 浏览器搜索乔拓云,登录乔拓云网后台,…...

谷歌最新医学领域LLM大模型:AMIE
2024年1月11日Google 研究院发布最新医疗大模型AMIE:用于诊断医学推理和对话的研究人工智能系统。 文章链接:Articulate Medical Intelligence Explorer (AMIE) giuthub:目前代码未开源 关于大模型之前有过一篇总结:大语言模型(L…...

路由器02_静态路由DHCP
一、静态路由 1、静态路由特点 由管理员手工配置,是单向的,缺乏灵活性 2、默认路由 默认路由是一种比较特殊静态路由,一般用于末节(末梢)网络,直接指定目标为任何地方 二、静态…...

Mysql 递归查询所有子节点,hutool树形结构封装
工作中经常会有像目录,部门的多级结构,记录一下查询自己点的方式,留着复制粘贴 方式1: SELECT* FROMcus_department WHEREFIND_IN_SET( id, pid ) > 0;UNIONSELECTcd.* FROM( SELECT * FROM cus_department WHERE pid IS …...

【代码随想录04】24. 两两交换链表中的节点 19. 删除链表的倒数第 N 个结点 面试题 02.07. 链表相交 142. 环形链表 II
24. 两两交换链表中的节点 题目描述 给你一个链表,两两交换其中相邻的节点,并返回交换后链表的头节点。你必须在不修改节点内部的值的情况下完成本题(即,只能进行节点交换)。 做题思路 可以设置虚拟头结点cur和画图…...

Pandas实战100例 | 案例 25: 计算相关系数
案例 25: 计算相关系数 知识点讲解 在统计分析中,了解变量之间的关系是非常重要的。相关系数是衡量变量之间线性相关程度的一种方法。Pandas 提供了 corr 方法来计算列之间的相关系数。 相关系数: 相关系数的值范围在 -1 到 1 之间。接近 1 表示正相关࿰…...

vue文本识别“\n“换行问题的解决方式
一、通过 css属性 实现 设置 white-space: pre-wrap; 代码如下: <div style"white-space: pre-wrap;">({含有\n的字符串}}</div> 扩展: white-space属性值: 值描述normal默认。空白会被浏览器忽略。pre空白会被浏…...
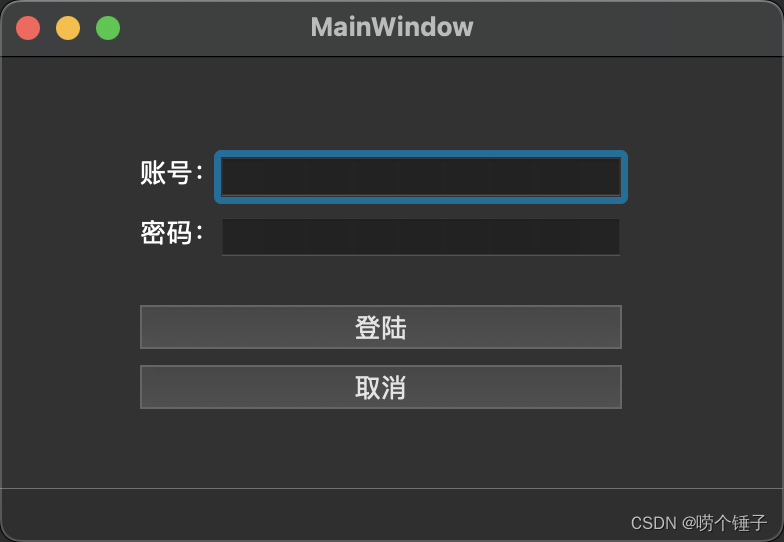
【QT-UI】
1.使用手动连接,将登录框中的取消按钮使用qt4版本的连接到自定义的槽函数中,在自定义的槽函数中调用关闭函数 #include "mainwindow.h" #include "ui_mainwindow.h"MainWindow::MainWindow(QWidget *parent): QMainWindow(parent), …...

MyBatisPlus逆向工程
依赖 <!--Mybatis-plus逆向生成器依赖--><dependency><groupId>com.baomidou</groupId><artifactId>mybatis-plus-generator</artifactId><version>3.4.1</version></dependency><!--Mybatis-plus逆向生成器的Freema…...
层)
创建ESP32开源WiFi MAC(介质访问控制)层
内置WiFi 内置的 WiFi.h 库将使我们能够轻松使用 ESP32 板的 WiFi 功能。 连接到 Wi-Fi 接入点: #include <WiFi.h>const char* ssid "yourNetworkName"; const char* password "yourNetworkPassword";void setup(){Serial.begin(11…...

Vue3 + Element Plus + TypeScript中el-transfer穿梭框组件使用详解及示例
使用详解 Element Plus 的 el-transfer 组件是一个强大的穿梭框组件,常用于在两个集合之间进行数据转移,如权限分配、数据选择等场景。下面我将详细介绍其用法并提供一个完整示例。 核心特性与用法 基本属性 v-model:绑定右侧列表的值&…...

Cesium1.95中高性能加载1500个点
一、基本方式: 图标使用.png比.svg性能要好 <template><div id"cesiumContainer"></div><div class"toolbar"><button id"resetButton">重新生成点</button><span id"countDisplay&qu…...

2024年赣州旅游投资集团社会招聘笔试真
2024年赣州旅游投资集团社会招聘笔试真 题 ( 满 分 1 0 0 分 时 间 1 2 0 分 钟 ) 一、单选题(每题只有一个正确答案,答错、不答或多答均不得分) 1.纪要的特点不包括()。 A.概括重点 B.指导传达 C. 客观纪实 D.有言必录 【答案】: D 2.1864年,()预言了电磁波的存在,并指出…...

质量体系的重要
质量体系是为确保产品、服务或过程质量满足规定要求,由相互关联的要素构成的有机整体。其核心内容可归纳为以下五个方面: 🏛️ 一、组织架构与职责 质量体系明确组织内各部门、岗位的职责与权限,形成层级清晰的管理网络…...

第25节 Node.js 断言测试
Node.js的assert模块主要用于编写程序的单元测试时使用,通过断言可以提早发现和排查出错误。 稳定性: 5 - 锁定 这个模块可用于应用的单元测试,通过 require(assert) 可以使用这个模块。 assert.fail(actual, expected, message, operator) 使用参数…...

【AI学习】三、AI算法中的向量
在人工智能(AI)算法中,向量(Vector)是一种将现实世界中的数据(如图像、文本、音频等)转化为计算机可处理的数值型特征表示的工具。它是连接人类认知(如语义、视觉特征)与…...
详解:相对定位 绝对定位 固定定位)
css的定位(position)详解:相对定位 绝对定位 固定定位
在 CSS 中,元素的定位通过 position 属性控制,共有 5 种定位模式:static(静态定位)、relative(相对定位)、absolute(绝对定位)、fixed(固定定位)和…...

c#开发AI模型对话
AI模型 前面已经介绍了一般AI模型本地部署,直接调用现成的模型数据。这里主要讲述讲接口集成到我们自己的程序中使用方式。 微软提供了ML.NET来开发和使用AI模型,但是目前国内可能使用不多,至少实践例子很少看见。开发训练模型就不介绍了&am…...

均衡后的SNRSINR
本文主要摘自参考文献中的前两篇,相关文献中经常会出现MIMO检测后的SINR不过一直没有找到相关数学推到过程,其中文献[1]中给出了相关原理在此仅做记录。 1. 系统模型 复信道模型 n t n_t nt 根发送天线, n r n_r nr 根接收天线的 MIMO 系…...

在web-view 加载的本地及远程HTML中调用uniapp的API及网页和vue页面是如何通讯的?
uni-app 中 Web-view 与 Vue 页面的通讯机制详解 一、Web-view 简介 Web-view 是 uni-app 提供的一个重要组件,用于在原生应用中加载 HTML 页面: 支持加载本地 HTML 文件支持加载远程 HTML 页面实现 Web 与原生的双向通讯可用于嵌入第三方网页或 H5 应…...
