二分图最大匹配——匈牙利算法详解
文章目录
- 零、前言
- 一、红娘牵线
- 二、二分图最大匹配
- 2.1概念
- 2.2交替路
- 2.3增广路
- 2.4匈牙利算法
- 2.4.1算法原理
- 2.4.2算法示例
- 2.4.3代码实现
- 3.OJ练习
- 3.1模板
- 3.2棋盘覆盖
- 3.3車的放置
零、前言
关于二分图的基本知识见:二分图及染色法判定
一、红娘牵线
一位红娘近日遇到一群暧昧男女,被请求成全他们,经验丰富的红娘观察到一名男生可能有多名青睐的女生,一名女生也可能有多名青睐的男生,但是出于道德伦理要求,显然只能两两男女配对,为了尽可能使大家满意,她要尽可能地成全多对男女。经过观察,她发现这些男女间地暧昧关系如下(连线代表互相青睐):
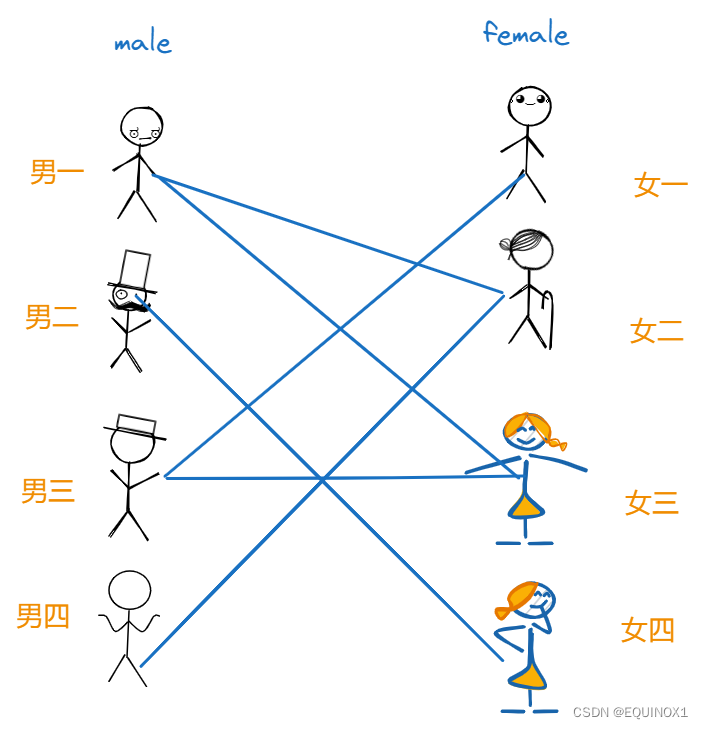
红娘根据经验快速地进行了一次配对,男一配女二,男儿配女四,男三配女三。
(下图红色连线代表配对,此时女一和男四没有配对)
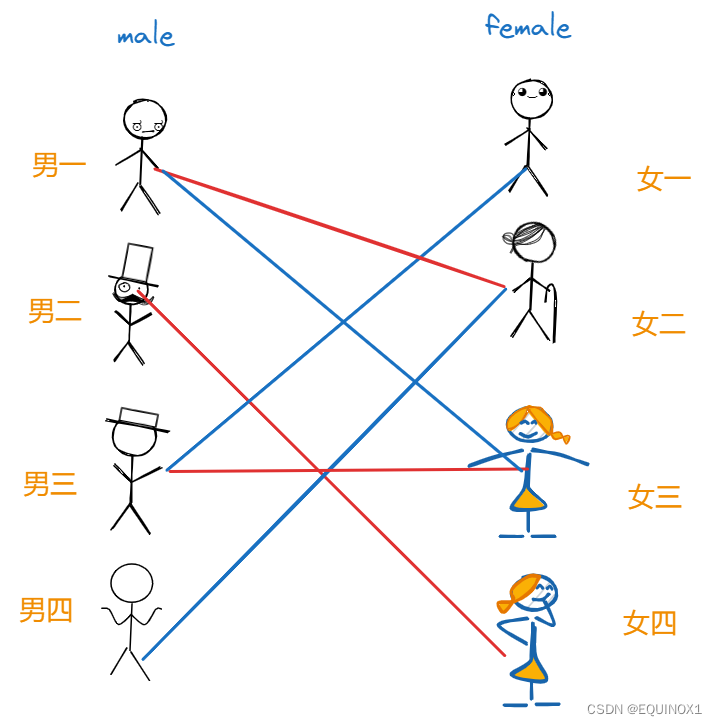
配对的三对男女自然很满意,此时女一和男四悻悻地来找红娘,说他们两个怎么办,红娘看二人不愿凑合都想有心仪的归宿,男四只愿跟女二在一起,女一只愿跟男三在一起。
红娘于是只得回头看已经配对的三对男女,发现男一似乎对女三也有意思,但是女三已经跟男三配对了,于是红娘私底下找到男三,问他愿不愿意将女三让给男一,自己可以帮他跟女一牵线,男三一看这敢情好,直接答应,于是男三的对象变为了女一,男一的对象变为了女三,男四趁虚而入,和女二配对,于是有了下面的局面:
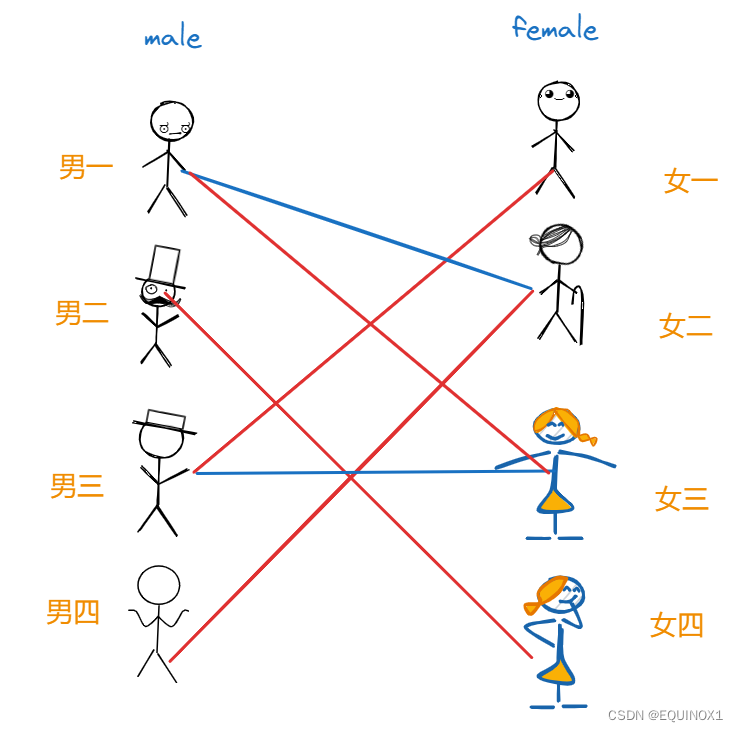
至此,每个人都有和自己的心仪对象之一配了对,中间虽有ntr波折,但结局皆大欢喜。
二、二分图最大匹配
2.1概念
“任意两条边都没有公共端点”的边的集合被称为图的一组匹配。在二分图中,包含边数最多的一组匹配被称为二分图的最大匹配。
上面的红娘牵线其实就是二分图的最大匹配的形象示例。
我们称匹配的边为匹配边,匹配边的两个端点为匹配点,相应的自然有了非匹配边和非匹配点的概念。
2.2交替路
从一个非匹配点出发,依次经过非匹配边、匹配边、非匹配边形成的路径叫交替路。
2.3增广路
从一个未匹配点出发,走交替路,若能到达另一个未匹配点,则这条交替路称为增广路。
增广路显然有如下性质:
- 长度len为奇数
- 路径上第1、3、5……len条边是非匹配边,第2、4……len - 1条边是匹配边
正因为以上性质,如果我们把路径上所有边的状态取反,原来的匹配边变成非匹配边,原来的非匹配边变成匹配边,那么得到的新的边集仍然是一组匹配,并且匹配边数+1.
从而得到以下推论:
二分图的一组匹配是最大匹配,当且仅当图中不存在包含该匹配的增广路。
2.4匈牙利算法
**匈牙利算法(Hungary Algorithm)**又称牛头人算法增广路算法,用于计算二分图的最大匹配。
2.4.1算法原理
算法流程十分简单:
- 设匹配边集S = Ø,即所有边都是非匹配边
- 找到增广路path,将增广路上所有边状态取反,得到更大的匹配S‘
- 重复2,直到没有增广路
算法的关键在于如何找到增广路。
我们将二分图的点分为左部节点和右部节点,匈牙利算法依次尝试给给每一个左部节点u寻找一个匹配的右部节点v。右部节点v能和左部节点u匹配需要满足以下两个条件之一:
- v本身就是非匹配点
- 此时u~v为长度为1的增广路
- v已经跟左部节点u’匹配,但是从u‘出发能找到另一个右部节点v’和其匹配。
- 此时uvu‘~v’就是一条增广路
在具体的程序实现中,我们采用深度优先搜索的框架,递归的从u出发去找增广路,若找到,则在回溯时,正好把路径上的匹配状态取反。另外,可以用全局标记数组来维护节点的访问情况,避免重复搜索。
匈牙利算法的正确性基于贪心策略,它的一个重要特点是:当一个节点成为匹配点后,至多因为找到增广路而更换匹配对象,但是绝不会再变回非匹配点。
对于每个左部节点,寻找增广路最多遍历整张二分图一次。因此,该算法的时间复杂度为O(nm),其中n为点数目,m为边数目。
2.4.2算法示例
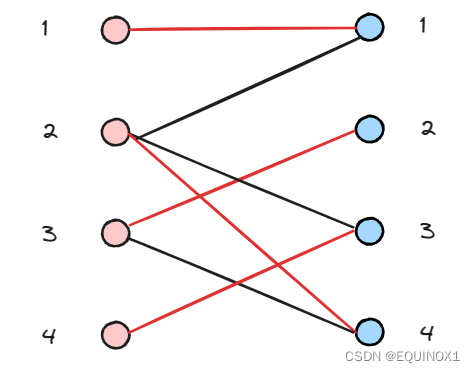
有二分图如下,左部节点1、2、3、4,右部节点1、2、3、4
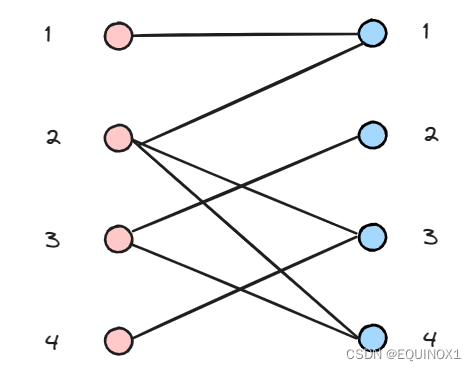
左1匹配右1
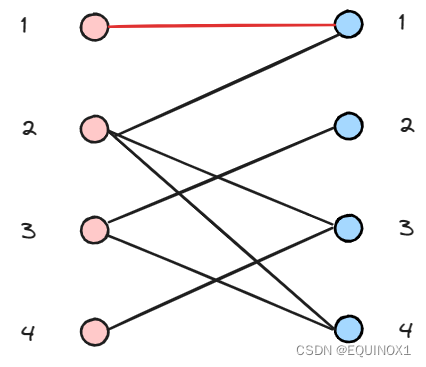
左2尝试匹配右1失败
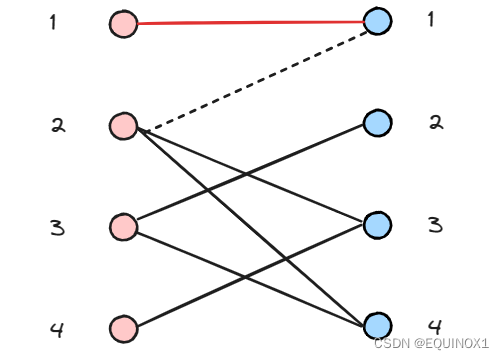
左2匹配右3

左3匹配右2
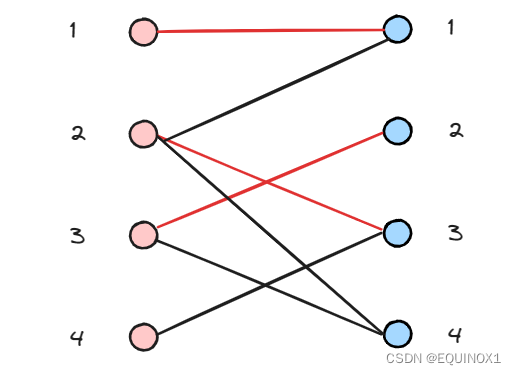
左4尝试匹配右3,递归左2尝试匹配右1失败
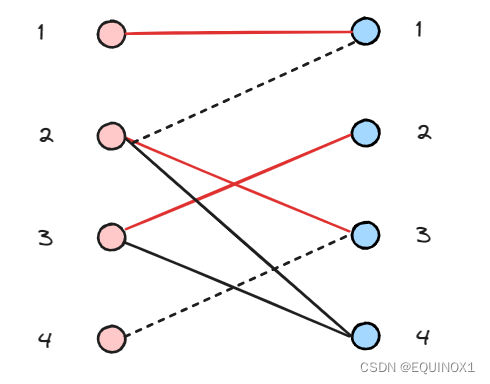
左2继续尝试匹配右4,成功找到增广路

回溯时把增广路取反,左4得以匹配右3
2.4.3代码实现
bool dfs(int u)
{for (int i = head[u]; ~i; i = edges[i].nxt){int v = edges[i].v;if (vis[v])continue;vis[v] = 1;if (!match[v] || dfs(match[v])){match[v] = u;return true;}}return false;
}
//main
for (int i = 1; i <= n; i++)
{memset(vis, 0, sizeof(vis));if (dfs(i))cnt++;
}
3.OJ练习
二分图匹配的模型有两个要素:
1.节点能分成独立的两个集合,每个集合内部有0条边。
2.每个节点只能与1条匹配边相连。
我们把它简称为“0要素”和“1要素”。在把实际问题抽象成二分图匹配时,我们就要寻找题目中具有这种“0”和“1”性质的对象,从而发现模型构建的突破口。
3.1模板
P3386 【模板】二分图最大匹配 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)
洛谷模板题,检验以下自己的匈牙利算法板子是否正确,以便于在后续问题中使用。
#include <iostream>
#include <cstring>
#include <queue>
#include <algorithm>
#include <string>
using namespace std;
using pii = pair<int, int>;
#define N 510
#define M 50010
struct edge
{int v, nxt;
} edges[M << 1];
int head[N], match[N]{0}, idx = 0, n, m, e, a, b, cnt = 0;
bool vis[N];
void addedge(int u, int v)
{edges[idx] = {v, head[u]};head[u] = idx++;
}
bool dfs(int u)
{for (int i = head[u]; ~i; i = edges[i].nxt){int v = edges[i].v;if (vis[v])continue;vis[v] = 1;if (!match[v] || dfs(match[v])){match[v] = u;return true;}}return false;
}
signed main()
{ios::sync_with_stdio(false);cin.tie(0), cout.tie(0);// freopen("in.txt", "r", stdin);// freopen("out.txt", "w", stdout);memset(head, -1, sizeof(head));cin >> n >> m >> e;for (int i = 1; i <= e; i++){cin >> a >> b;addedge(a, b);}for (int i = 1; i <= n; i++){memset(vis, 0, sizeof(vis));if (dfs(i))cnt++;}cout << cnt;return 0;
}
3.2棋盘覆盖
372. 棋盘覆盖 - AcWing题库
首先对于一个矩阵而言,我们根据行列坐标相加的奇偶性可以对其进行二染色,并且任何一个格子和其四个方向上的相邻格子颜色不同。
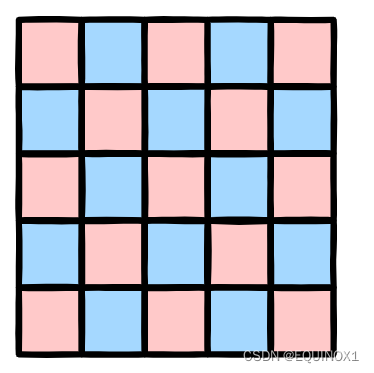
这样我们就可以将问题抽象为二分图匹配问题。
0要素:同色格子之间无边 1要素:每个格子只能被一张骨牌覆盖
一个骨牌一定是覆盖了两个颜色不同的方格,我们按照颜色将格子分为左部点和右部点,被骨牌覆盖的两个左右部点即为一个匹配,求最多的骨牌数目就是求最大匹配。
基本上还是板子题,由于数据量很小所以用了邻接矩阵,由于有的格子不能放置,所以要加个条件。
奇数格子还是偶数格子作为左部点没有区别。
直接看代码:
#include <iostream>
#include <cstring>
#include <queue>
#include <algorithm>
#include <string>
using namespace std;
using pii = pair<int, int>;
#define N 110
#define M 50010
int n, t, a, b, cnt = 0, dir[5]{1, 0, -1, 0, 1};pii match[N][N];
bool g[N][N], vis[N][N];
bool dfs(int x, int y)
{for (int i = 0; i < 4; i++){int nx = x + dir[i], ny = y + dir[i + 1];int pos = (nx - 1) * n + ny;if (nx < 1 || ny < 1 || nx > n || ny > n || vis[nx][ny] || g[nx][ny])continue;vis[nx][ny] = 1;if (match[nx][ny].first == -1 || dfs(match[nx][ny].first, match[nx][ny].second)){match[nx][ny] = {x, y};return true;}}return false;
}
signed main()
{ios::sync_with_stdio(false);cin.tie(0), cout.tie(0);memset(g, 0, sizeof(g));memset(match, -1, sizeof(match));cin >> n >> t;while (t--){cin >> a >> b;g[a][b] = 1;}for (int i = 1; i <= n; i++){for (int j = (i & 1) ? 1 : 2; j <= n; j += 2){if (!g[i][j]){memset(vis, 0, sizeof(vis));if (dfs(i, j))cnt++;}}}cout << cnt;return 0;
}
3.3車的放置
373. 車的放置 - AcWing题库
1要素:每行每列只能有一个车,对于(i,j)放置车,相当于i行j列都被占用,即i行和j列连边
0要素:一个车不能既在第i行又在第j行,所以行与行之间无边
#include <iostream>
#include <cstring>
#include <queue>
#include <algorithm>
#include <string>
using namespace std;
using pii = pair<int, int>;
#define N 210
#define M 50010
int n, m, t, a, b, cnt = 0, dir[5]{1, 0, -1, 0, 1};int match[N]{0};
bool g[N][N]{0}, vis[N];
bool dfs(int i)
{for (int j = 1; j <= m; j++){if (g[i][j] || vis[j])continue;vis[j] = 1;if (!match[j] || dfs(match[j])){match[j] = i;return true;}}return false;
}
signed main()
{ios::sync_with_stdio(false);cin.tie(0), cout.tie(0);cin >> n >> m >> t;while (t--){cin >> a >> b;g[a][b] = 1;}for (int i = 1; i <= n; i++){memset(vis, 0, sizeof(vis));if (dfs(i))cnt++;}cout << cnt;return 0;
}
相关文章:

二分图最大匹配——匈牙利算法详解
文章目录 零、前言一、红娘牵线二、二分图最大匹配2.1概念2.2交替路2.3增广路2.4匈牙利算法2.4.1算法原理2.4.2算法示例2.4.3代码实现 3.OJ练习3.1模板3.2棋盘覆盖3.3車的放置 零、前言 关于二分图的基本知识见:二分图及染色法判定 一、红娘牵线 一位红娘近日遇到一…...

【AI视野·今日Robot 机器人论文速览 第七十一期】Fri, 5 Jan 2024
AI视野今日CS.Robotics 机器人学论文速览 Fri, 5 Jan 2024 Totally 11 papers 👉上期速览✈更多精彩请移步主页 Daily Robotics Papers Machine Learning in Robotic Ultrasound Imaging: Challenges and Perspectives Authors Yuan Bi, Zhongliang Jiang, Felix D…...

xtu oj 1334 Least Common Multiple
题目描述 一个集合,任取3个不同的元素,求其最小公倍数中最小的值是多少? 输入 第一行是样例数T(1≤T≤100)。 每个样例的第一行是一个整数n(3≤n≤50),表示集合元素的个数。 每个样例的第二行是n个整数a1,a2,…,an,1≤ai≤106。…...
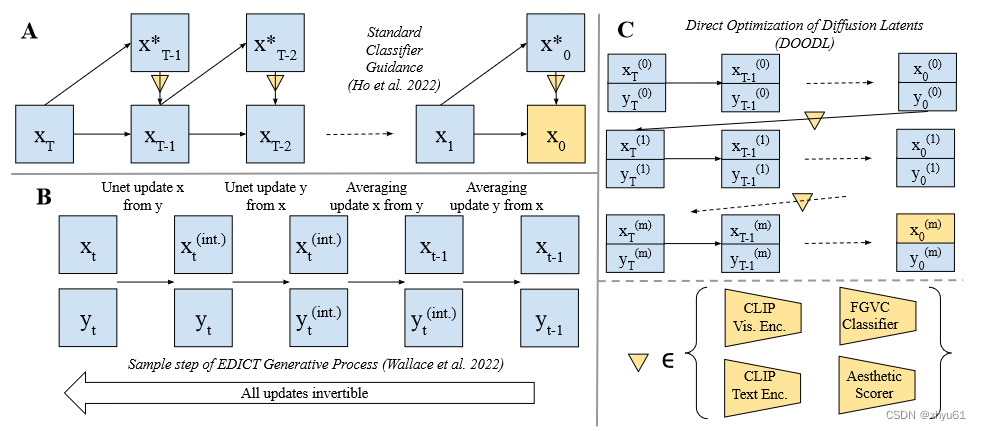
【论文笔记】End-to-End Diffusion Latent Optimization Improves Classifier Guidance
Abstract Classifier guidance为图像生成带来了控制,但是需要训练新的噪声感知模型(noise-aware models)来获得准确的梯度,或使用最终生成的一步去噪近似,这会导致梯度错位(misaligned gradients)和次优控制(sub-optimal control)。 梯度错位…...
【HarmonyOS4.0】第四篇-ArkUI基础实战
一、ArkUI框架简介 ArkUI开发框架是方舟开发框架的简称,它是一套构建 HarmonyOS / OpenHarmony 应用界面的声明式UI开发框架,它使用极简的UI信息语法、丰富的UI组件以及实时界面语言工具,帮助开发者提升应用界面开发效率 30%,开发…...

每日一题——LeetCode1128.等价多米诺骨牌对的数量
先尝试暴力解法: var numEquivDominoPairs function(dominoes) {var count0for(let i0;i<dominoes.length-1;i){for(let ji1;j<dominoes.length;j){if((dominoes[i][0]dominoes[j][0] && dominoes[i][1]dominoes[j][1]) || (dominoes[i][0]dominoes…...
关联规则分析(Apriori算法2
目录 1.核心术语:2.强关联规则:小结: 1.核心术语: 支持度(Support):指项集出现的频繁程度(相当于项集出现的概率) 最小支持度有绝对值和占比两种表示方式 置信度&#…...
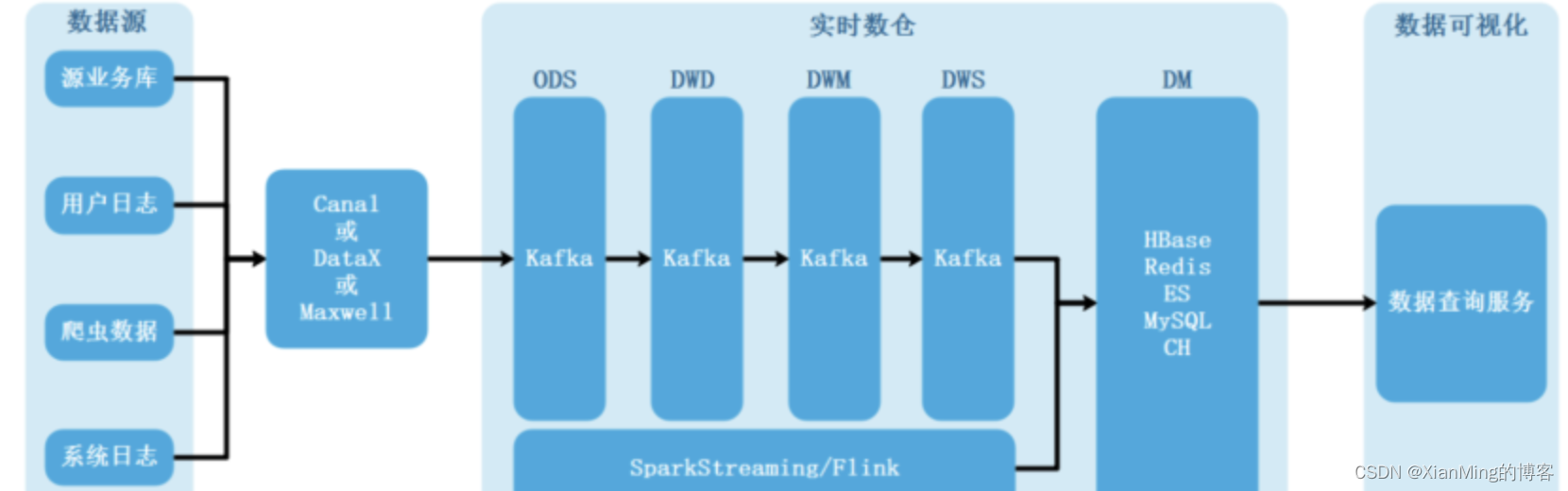
数据仓库(2)-认识数仓
1、数据仓库是什么 数据仓库 ,由数据仓库之父比尔恩门(Bill Inmon)于1990年提出,主要功能仍是将组织透过资讯系统之联机事务处理(OLTP)经年累月所累积的大量资料,透过数据仓库理论所特有的资料储存架构,做…...

C#编程-实现委托
实现委托 委托是可以存储对方法的引用的对象。在C#中,委托允许您动态地改变类中方法的引用。 考虑咖啡售货机的示例,它配置不同口味的咖啡,例如卡布奇诺咖啡和黑咖啡。在选择所需口味的咖啡时,售货机决定混合各种成分,例如奶粉、咖啡粉、热水、卡布奇诺咖啡粉。所有的材…...
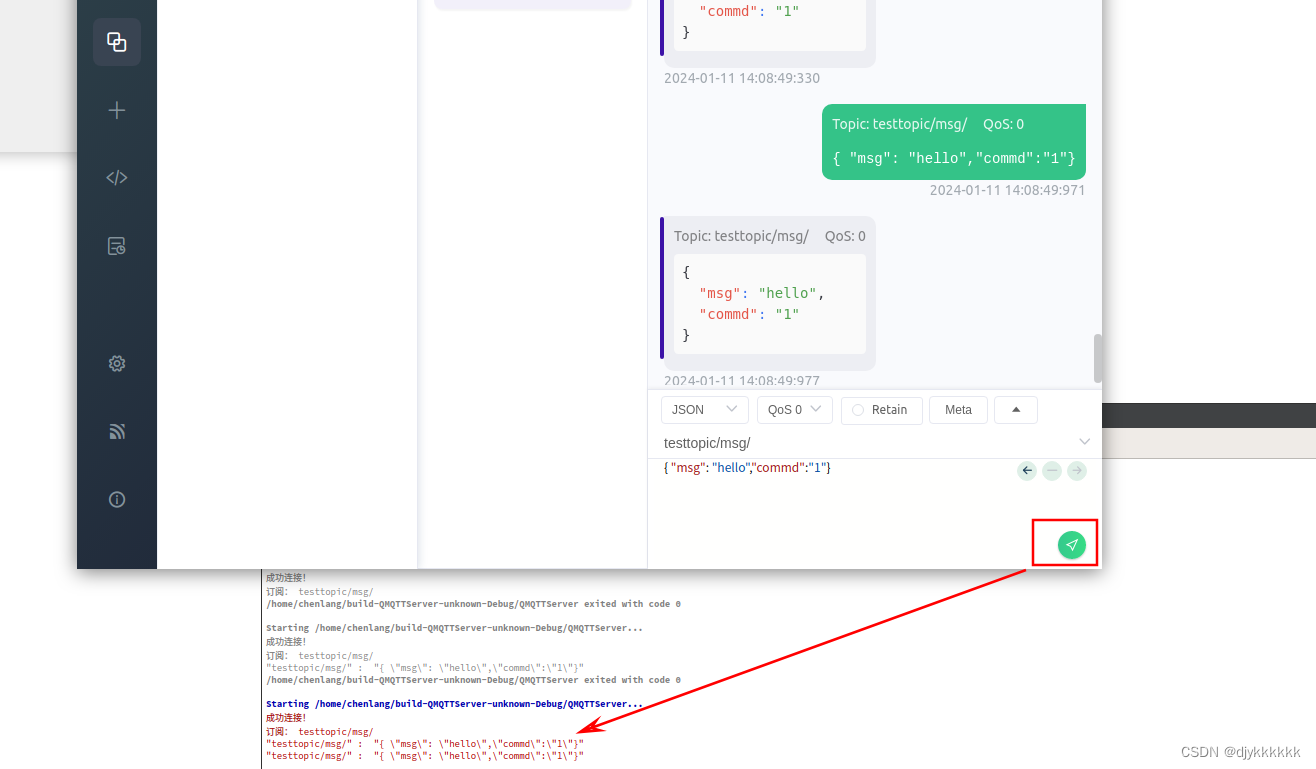
Ubuntu18.04 Qt 实现MQTT
什么是MQTT? 作用是什么(适用场景)? 与其他通讯协议相比,优缺点在那里? 一.安装 MQTT 服务器 使用 EMQ X(开源且可视化管理) 下载 EMQX 下载的是 emqx-5.0.26-ubuntu18.04-…...

【软件测试】学习笔记-不同视角的软件性能与性能指标
本篇文章探讨新的测试主题:性能测试,因为性能测试的专业性很强,所以我会以从0到1的入门者视角,系统性地阐述性能测试的方法以及应用领域,用实例去诠释各种性能指标。 本篇文章站在全局的视角,帮你梳理软件性…...
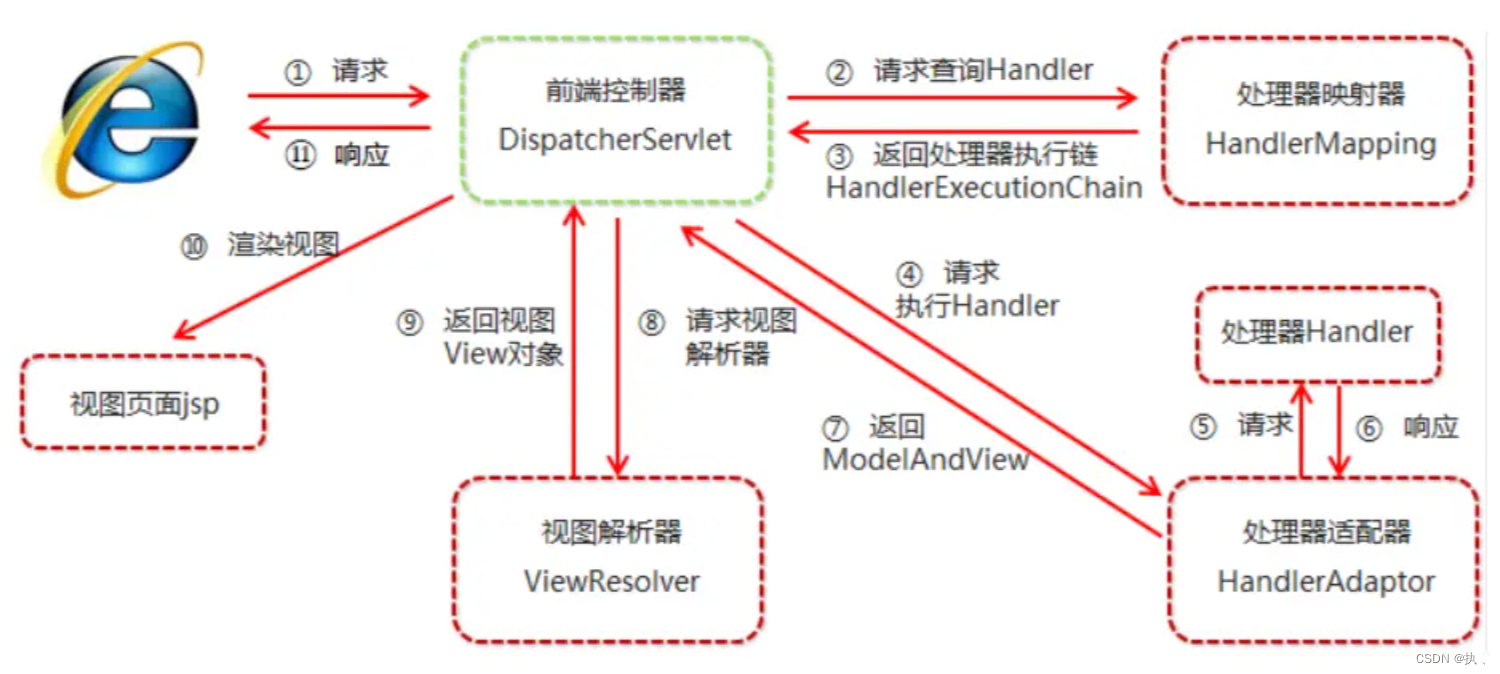
Spring MVC组件
1.DispatcherServlet前端控制器 用户请求到达前端控制器,它就相当于mvc模式中的c,dispatcherServlet 是整个流程控制的中心,由它调用其它组件处理用户的请求,dispatcherServlet 的存在降低了组件之间的耦合性。 2.HandlerMappin…...

vue文件在<template>中使用多个<el-main>报错(已解决)
目录 1.原理 2. 根据你的需求,自定义每个 组件的内容。你可以在 标签内部插入文本、其他组件、样式等。 3. 根据需要添加样式或其他属性到每个 组件。你可以使用 class、style 或其他属性来自定义每个组件的外观和行为。 4.一个可以运行的总代码如下 5.我的一…...
【PlantUML】- 时序图
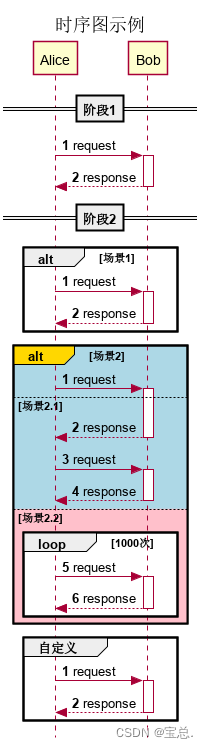
写在前面 本篇文章,我们来介绍一下PlantUML的时序图。这个相对类图来讲,比较简单,也不需要布局。读完文章,相信你就能实际操作了。 目录 写在前面一、基本概念二、具体步骤1.环境说明2.元素3.语法4.示例 三、参考资料写在后面系列…...

openai自定义API操作 API (openai.custom):OpenAI API 实现电商平台的智能库存管理
在电商行业中,库存管理是至关重要的环节之一。一个高效的库存管理系统可以确保商品的正常供应,避免缺货或积压现象,从而提高销售效率和客户满意度。然而,传统的库存管理方式往往存在一些问题,如数据不准确、响应不及时…...
宠物服务新篇章:预约小程序带来的变革
随着科技的进步和互联网的普及,小程序已经成为了一种非常受欢迎的应用形式。对于宠物门店来说,开发一个预约小程序可以大大提高客户体验和管理效率。下面是一份宠物门店预约小程序的开发指南。 浏览器搜索乔拓云,登录乔拓云网后台,…...

谷歌最新医学领域LLM大模型:AMIE
2024年1月11日Google 研究院发布最新医疗大模型AMIE:用于诊断医学推理和对话的研究人工智能系统。 文章链接:Articulate Medical Intelligence Explorer (AMIE) giuthub:目前代码未开源 关于大模型之前有过一篇总结:大语言模型(L…...

路由器02_静态路由DHCP
一、静态路由 1、静态路由特点 由管理员手工配置,是单向的,缺乏灵活性 2、默认路由 默认路由是一种比较特殊静态路由,一般用于末节(末梢)网络,直接指定目标为任何地方 二、静态…...

Mysql 递归查询所有子节点,hutool树形结构封装
工作中经常会有像目录,部门的多级结构,记录一下查询自己点的方式,留着复制粘贴 方式1: SELECT* FROMcus_department WHEREFIND_IN_SET( id, pid ) > 0;UNIONSELECTcd.* FROM( SELECT * FROM cus_department WHERE pid IS …...

【代码随想录04】24. 两两交换链表中的节点 19. 删除链表的倒数第 N 个结点 面试题 02.07. 链表相交 142. 环形链表 II
24. 两两交换链表中的节点 题目描述 给你一个链表,两两交换其中相邻的节点,并返回交换后链表的头节点。你必须在不修改节点内部的值的情况下完成本题(即,只能进行节点交换)。 做题思路 可以设置虚拟头结点cur和画图…...

AI-调查研究-01-正念冥想有用吗?对健康的影响及科学指南
点一下关注吧!!!非常感谢!!持续更新!!! 🚀 AI篇持续更新中!(长期更新) 目前2025年06月05日更新到: AI炼丹日志-28 - Aud…...

在HarmonyOS ArkTS ArkUI-X 5.0及以上版本中,手势开发全攻略:
在 HarmonyOS 应用开发中,手势交互是连接用户与设备的核心纽带。ArkTS 框架提供了丰富的手势处理能力,既支持点击、长按、拖拽等基础单一手势的精细控制,也能通过多种绑定策略解决父子组件的手势竞争问题。本文将结合官方开发文档,…...

AtCoder 第409场初级竞赛 A~E题解
A Conflict 【题目链接】 原题链接:A - Conflict 【考点】 枚举 【题目大意】 找到是否有两人都想要的物品。 【解析】 遍历两端字符串,只有在同时为 o 时输出 Yes 并结束程序,否则输出 No。 【难度】 GESP三级 【代码参考】 #i…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个医院挂号小程序
一、开发准备 环境搭建: 安装DevEco Studio 3.0或更高版本配置HarmonyOS SDK申请开发者账号 项目创建: File > New > Create Project > Application (选择"Empty Ability") 二、核心功能实现 1. 医院科室展示 /…...

服务器硬防的应用场景都有哪些?
服务器硬防是指一种通过硬件设备层面的安全措施来防御服务器系统受到网络攻击的方式,避免服务器受到各种恶意攻击和网络威胁,那么,服务器硬防通常都会应用在哪些场景当中呢? 硬防服务器中一般会配备入侵检测系统和预防系统&#x…...

ServerTrust 并非唯一
NSURLAuthenticationMethodServerTrust 只是 authenticationMethod 的冰山一角 要理解 NSURLAuthenticationMethodServerTrust, 首先要明白它只是 authenticationMethod 的选项之一, 并非唯一 1 先厘清概念 点说明authenticationMethodURLAuthenticationChallenge.protectionS…...

成都鼎讯硬核科技!雷达目标与干扰模拟器,以卓越性能制胜电磁频谱战
在现代战争中,电磁频谱已成为继陆、海、空、天之后的 “第五维战场”,雷达作为电磁频谱领域的关键装备,其干扰与抗干扰能力的较量,直接影响着战争的胜负走向。由成都鼎讯科技匠心打造的雷达目标与干扰模拟器,凭借数字射…...

网络编程(UDP编程)
思维导图 UDP基础编程(单播) 1.流程图 服务器:短信的接收方 创建套接字 (socket)-----------------------------------------》有手机指定网络信息-----------------------------------------------》有号码绑定套接字 (bind)--------------…...

C++八股 —— 单例模式
文章目录 1. 基本概念2. 设计要点3. 实现方式4. 详解懒汉模式 1. 基本概念 线程安全(Thread Safety) 线程安全是指在多线程环境下,某个函数、类或代码片段能够被多个线程同时调用时,仍能保证数据的一致性和逻辑的正确性…...

AspectJ 在 Android 中的完整使用指南
一、环境配置(Gradle 7.0 适配) 1. 项目级 build.gradle // 注意:沪江插件已停更,推荐官方兼容方案 buildscript {dependencies {classpath org.aspectj:aspectjtools:1.9.9.1 // AspectJ 工具} } 2. 模块级 build.gradle plu…...
