计算机图形学作业:三维线段的图形变换
1. 将三维空间某线段 P1P2进行如下的操作,请按要求回答问题:
(1) 沿 X 轴、Y 轴和 Z 轴分别平移 dx、dy 和 dz 的长度,给出相应的变换矩阵。
变换矩阵为:
T=100001000010dxdydz1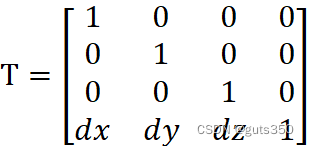
(2) 绕 X 轴旋转 alpha 度角,绕 Y 轴旋转 Beta 度角,绕 Z轴旋转 theta 度角,给出相应的变换矩阵。
变换矩阵(逆时针旋转)为:
T=10000cosαsinα00-sinαcosα00001 cosβ0-sinβ00100sinβ0cosβ00001cosθsinθ00-sinθcosθ0000100001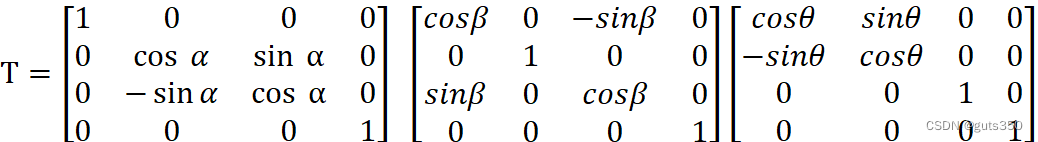
(3) 在保持 P1 点位置不变的情况下,将线段放大 s 倍,给出相应的变换矩阵。
设P1 点坐标为(x1,y1,z1)
变换矩阵为:
T=100001000010-x1-y1-z11 s0000s0000s00001100001000010x1y1z11
4) 依次完成(1)(2)(3)步的操作,给出相应的变换矩阵。
首先,沿 X 轴、Y 轴和 Z 轴分别平移 dx、dy 和 dz 的长度(设P1 点坐标为(x1,y1,z1)):
T=100001000010dxdydz1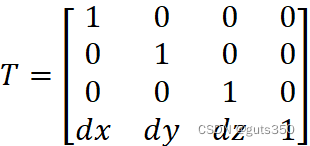
故
x'y'z'1=xyz1T![]()
然后,绕 X 轴旋转 alpha 度角,绕 Y 轴旋转 Beta 度角,绕 Z轴旋转 theta 度角:
令
R=10000cosαsinα00-sinαcosα00001 cosβ0-sinβ00100sinβ0cosβ00001cosθsinθ00-sinθcosθ0000100001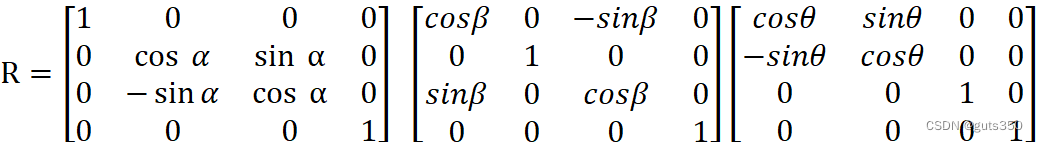
故
x''y''z''1=x'y'z'1R![]()
最后,保持 P1 点位置不变的情况下,将线段放大 s 倍,给出相应的变换矩阵:
设P1 点坐标此时为(x1’’,y1’’,z1’’),则
S=100001000010-x1''-y1''-z1''1 s0000s0000s00001100001000010x1''y1''z1''1
故
x'''y'''z'''1=x''y''z''1S![]()
(5) 以空间某线段 P3(x3,y3,z3)P4(x4,y4,z4)为轴旋转 alpha 度角,给出相应的变换矩阵。
1:平移旋转轴端点P3与坐标原点重合,相应变换矩阵为:
T=100001000010-x3-y3-z31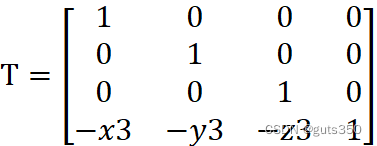
2:将旋转轴P3P4绕x轴逆时针旋转θ 度角使其落在xOz坐标平面上,然后绕y轴逆时针旋转β 度角使其与z轴重合,相应的变换矩阵为:
RXY=10000cosθsinθ00-sinθcosθ00001 cosβ0sinβ00100-sinβ0cosβ00001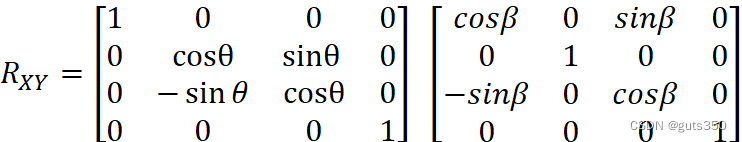
3:再绕z轴旋转α度角,相应的变换矩阵为:
RZ=cosαsinα00-sinαcosα0000100001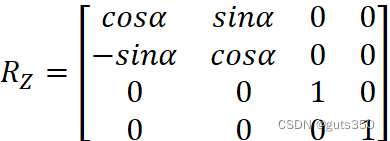
4:进行步骤2旋转变换的逆变换,相应的变换矩阵为:
RXY-1= cosβ0sinβ00100-sinβ0cosβ00001-110000cosθsinθ00-sinθcosθ00001-1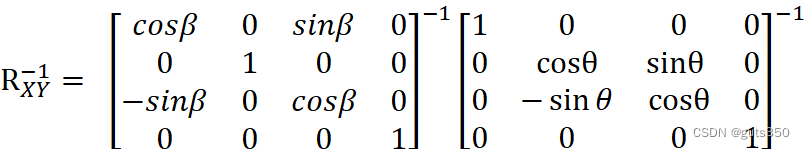
5:进行步骤1平移变换的逆变换,相应的变换矩阵为:
T'=100001000010x3y3z31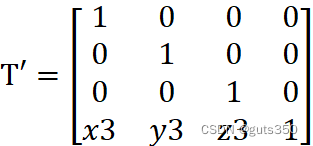
所以,以空间某线段 P3(x3,y3,z3)P4(x4,y4,z4)为轴旋转 alpha 度角,相应的变换矩阵为:
R=TRXYRZRXY-1T'![]()
相关文章:
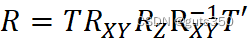
计算机图形学作业:三维线段的图形变换
1. 将三维空间某线段 P1P2进行如下的操作,请按要求回答问题: (1) 沿 X 轴、Y 轴和 Z 轴分别平移 dx、dy 和 dz 的长度,给出相应的变换矩阵。 变换矩阵为: T100001000010dxdydz1 (2)…...
)
Linux mren命令教程:批量重命名文件(附实际操作案例和注意事项)
Linux mren命令介绍 mren(全称multiple rename),它是用来对多个文件进行重命名的工具。这个命令在一次操作中可以批量改变多个文件的名称,特别是在需要对大量文件进行重命名时,mren将节省大量的时间和努力。 Linux m…...

LLVM系列(1): 在微软Visual Studio下编译LLVM
参考链接: Getting Started with the LLVM System using Microsoft Visual Studio — LLVM 18.0.0git documentation 1.安装visualstudio,版本需要大于vs2019 本机环境已安装visual studio2022,省略 2安装Makefile,版本需要大…...

分布式系统的三字真经CAP
文章目录 前言C(Consistency 数据一致性)A(Availability 服务可用性)P(Partition Tolerance 分区容错性)CAP理论最后 前言 你好,我是醉墨居士,我一起探索一下分布式系统的三字真经C…...

大模型背景下计算机视觉年终思考小结(一)
1. 引言 在过去的十年里,出现了许多涉及计算机视觉的项目,举例如下: 使用射线图像和其他医学图像领域的医学诊断应用使用卫星图像分析建筑物和土地利用率相关应用各种环境下的目标检测和跟踪,如交通流统计、自然环境垃圾检测估计…...
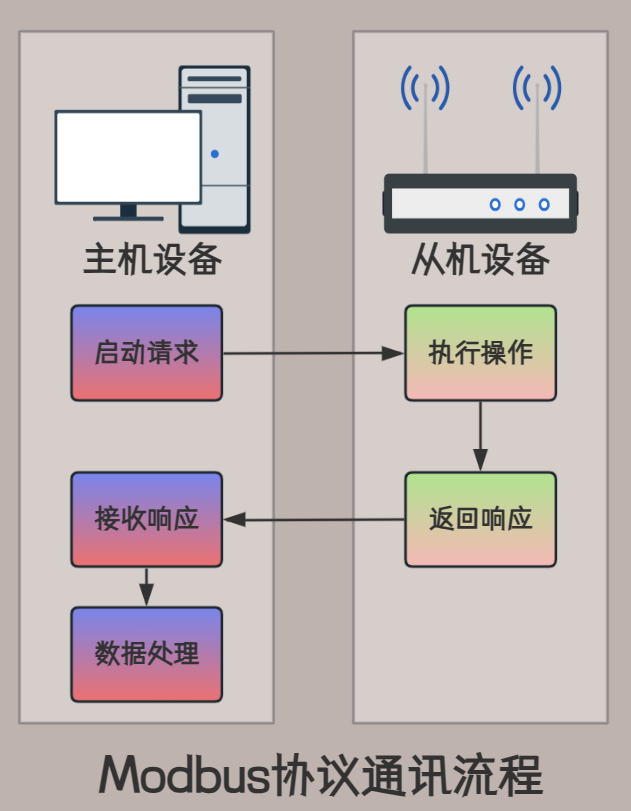
Modbus协议学习第一篇之基础概念
什么是“协议” 大白话解释:协议是用来正确传递消息数据而设立的一种规则。传递消息的双方(两台计算机)在通信时遵循同一种协议,即可理解彼此传递的消息数据。 Modbus协议模型 Modbus协议模型较为简单,使用一种称为应用…...
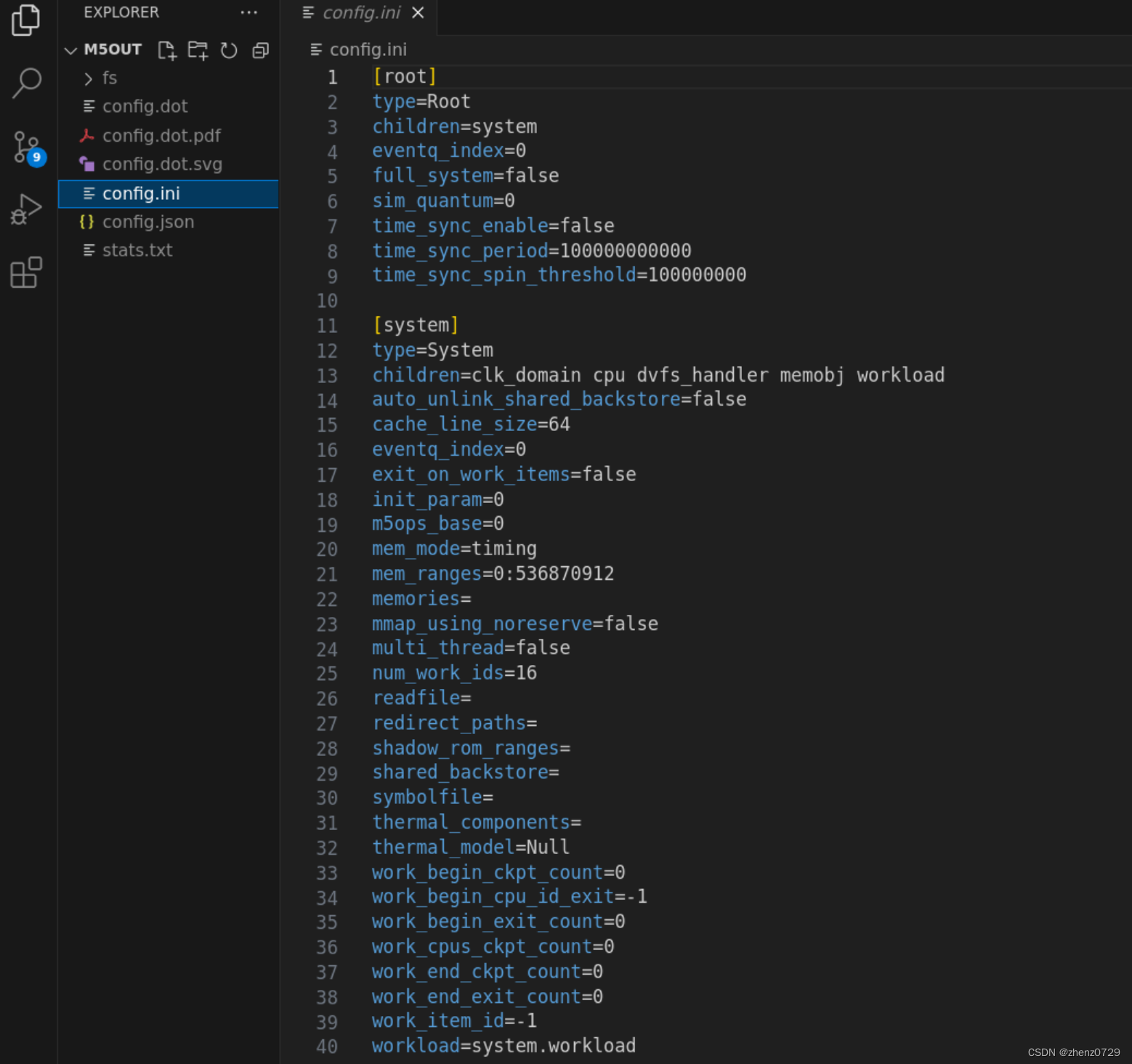
gem5学习(12):理解gem5 统计信息和输出——Understanding gem5 statistics and output
目录 一、config.ini 二、config.json 三、stats.txt 官方教程:gem5: Understanding gem5 statistics and output 在运行 gem5 之后,除了仿真脚本打印的仿真信息外,还会在根目录中名为 m5out 的目录中生成三个文件: config.i…...

索引的概述和使用
1、概述 索引占用存储空间,并不是越多越好,太多的索引会影响系统性能 索引分类 聚集索引: 逻辑顺序和物理顺序是一致的(表中行数的位置决定了该行在内存中存储的位置),因此效率优先于非聚集索引ÿ…...

力扣210. 课程表 II
深度优先遍历 思路: 搜索逻辑参见力扣207.课程表需要课程安排的顺序,课程搜索完成时,将其存储起来即可;存储课程的顺序需要注意: 输入依赖中 [A, B]图中表示 B -> A ,表示先 B 后 A&#x…...
[Docker] Mac M1系列芯片上完美运行Docker
docker pull qinchz/dm8-arm64 container_name: dm8ports:- "5236:5236"mem_limit: 1gmemswap_limit: 1gvolumes:- /data/dm8:/home/dmdba/data 数据库实例参数已修改,接近oracle使用习惯 #字符集 utf-8 CHARSET1 #VARCHAR 类型对象的长度以字符为单位 …...

CompletableFuture、ListenableFuture高级用列
CompletableFuture 链式 public static void main(String[] args) throws Exception {CompletableFuture<Integer> thenCompose T1().thenCompose(Compress::T2).thenCompose(Compress::T3);Integer result thenCompose.get();System.out.println(result);}// 假设这些…...
什么是云服务器,阿里云优势如何?
阿里云服务器ECS英文全程Elastic Compute Service,云服务器ECS是一种安全可靠、弹性可伸缩的云计算服务,阿里云提供多种云服务器ECS实例规格,如经济型e实例、通用算力型u1、ECS计算型c7、通用型g7、GPU实例等,阿里云百科aliyunbai…...

HCIA-Datacom题库(自己整理分类的)_15_VRP平台多选【9道题】
1.VRP操作平台存在哪些命令行视图? 用户视图 接口视图 协议视图 系统视图 2.以下哪些存储介质是华为路由器常用的存储介质 SDRAM NVRAM Flash Hard Disk SD Card 解析:Hard Disk是硬盘,一般网络设备没有。 3.VRP支持通过哪几种方式对路由器…...

html5基础入门
html5基础语法与标签 前言前端开发零基础入门介绍前端开发行业介绍:大前端时代:前端开发主要技术介绍学习方法IDE简介vscode快捷键: 总结 HTML语法与基础标签互联网基本原理HTTP协议(请求、响应)什么是前端、后端&…...
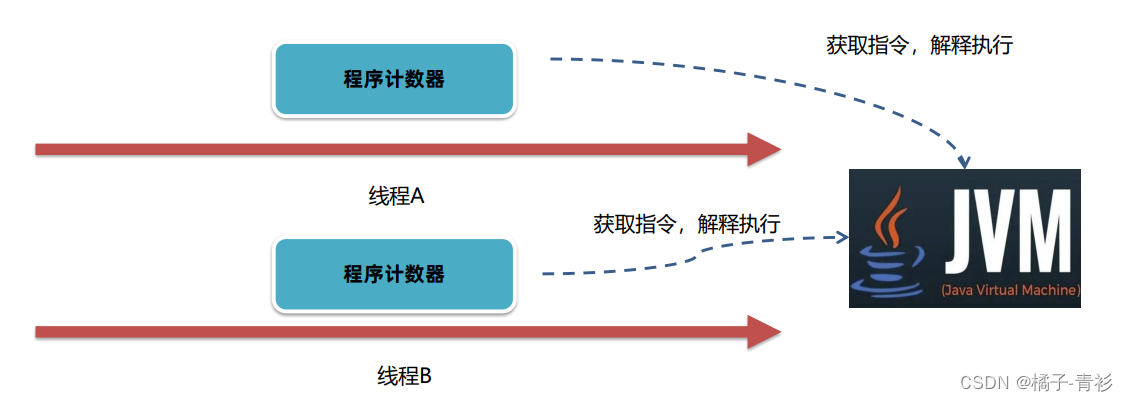
JVM工作原理与实战(十五):运行时数据区-程序计数器
专栏导航 JVM工作原理与实战 RabbitMQ入门指南 从零开始了解大数据 目录 专栏导航 前言 一、运行时数据区 二、程序计数器 总结 前言 JVM作为Java程序的运行环境,其负责解释和执行字节码,管理内存,确保安全,支持多线程和提供…...

计算机体系结构----存储系统
本文严禁转载,仅供学习使用。参考资料来自中国科学院大学计算机体系结构课程PPT以及《Digital Design and Computer Architecture》、《超标量处理器设计》、同济大学张晨曦教授资料。如有侵权,联系本人修改。 1.1 引言 1.1.1虚拟和物理内存 程序员看到…...
)
华为OD机试2024年最新题库(Python)
我是一名软件开发培训机构老师,我的学生已经有上百人通过了华为OD机试,学生们每次考完试,会把题目拿出来一起交流分享。 重要:2024年1月-5月,考的都是OD统一考试(C卷),题库已经整理…...

【打卡】牛客网:BM84 最长公共前缀
自己写的: 题目要求时间复杂度是o(n*len),说明可以遍历所有的字符。 空间复杂度o(1),说明不能用字符串存储公共前缀,所以用下标来记录。 调试过程: 大概花了20min。 我调试前的做法是,在while循环中&…...
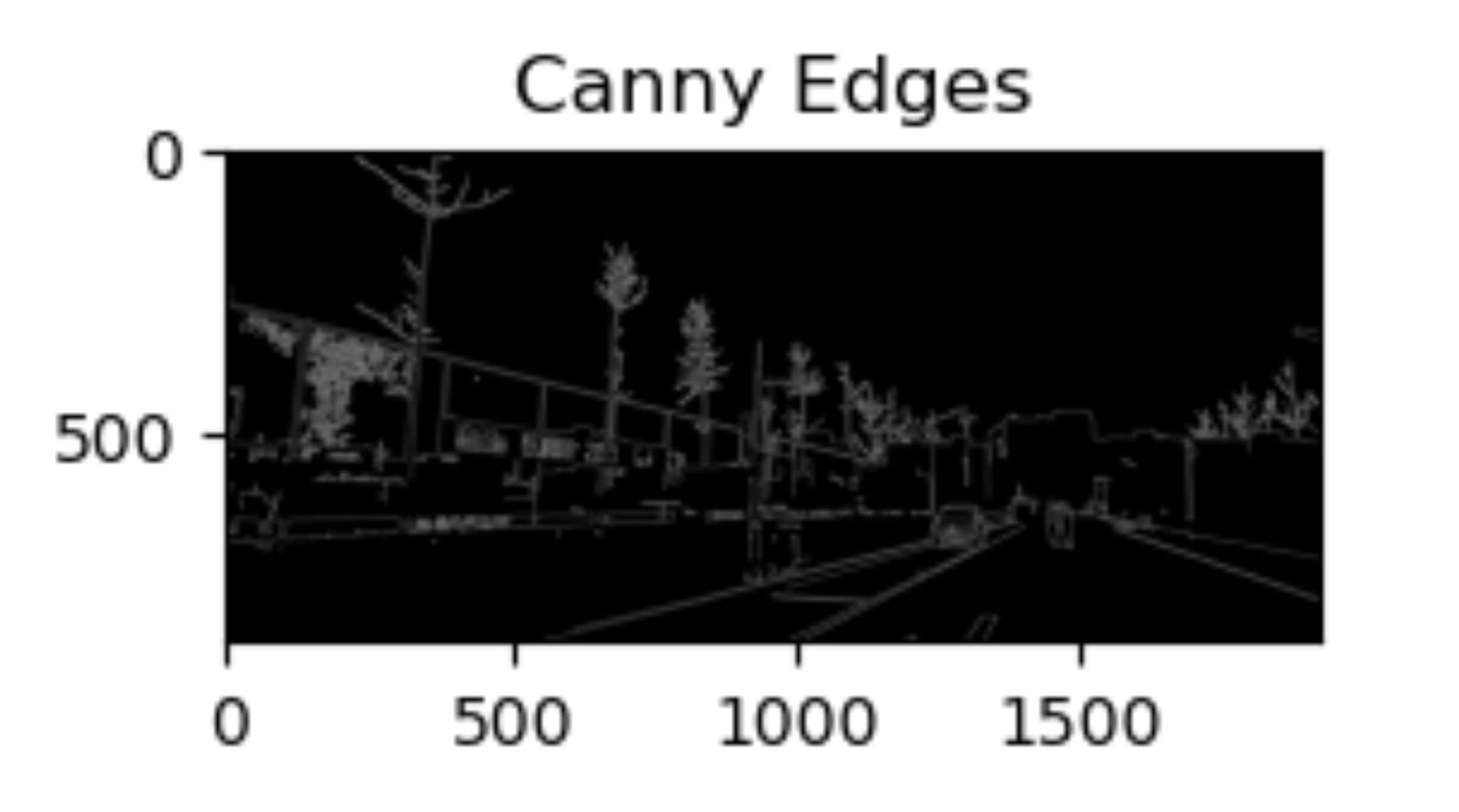
我在Vscode学OpenCV 图像处理三(图像梯度--边缘检测【图像梯度、Sobel 算子、 Scharr 算子、 Laplacian 算子、Canny 边缘检测】)
文章目录 一、图像梯度1.1 介绍1.2 涉及函数 二、高频强调滤波器2.1 Sobel 算子2.1.1 Sobel 理论基础2.1.2 Sobel 算子及函数使用(1)对参数取绝对值(2)控制dx,dy方向的求导阶数1. **计算 x 方向边缘(梯度&a…...
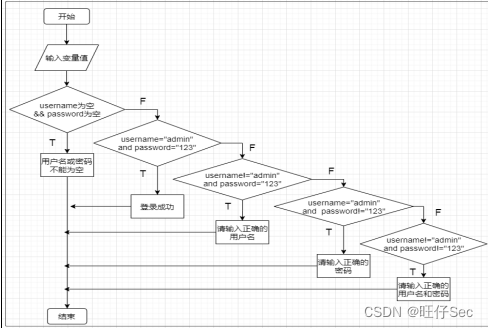
2023年全国职业院校技能大赛软件测试赛题—单元测试卷⑤
单元测试 一、任务要求 题目1:根据下列流程图编写程序实现相应处理,执行j10*x-y返回文字“j1:”和计算值,执行j(x-y)*(10⁵%7)返回文字“j2:”和计算值,执行jy*log(x10)返回文字“j3:”和计算值…...

React hook之useRef
React useRef 详解 useRef 是 React 提供的一个 Hook,用于在函数组件中创建可变的引用对象。它在 React 开发中有多种重要用途,下面我将全面详细地介绍它的特性和用法。 基本概念 1. 创建 ref const refContainer useRef(initialValue);initialValu…...

Oracle查询表空间大小
1 查询数据库中所有的表空间以及表空间所占空间的大小 SELECTtablespace_name,sum( bytes ) / 1024 / 1024 FROMdba_data_files GROUP BYtablespace_name; 2 Oracle查询表空间大小及每个表所占空间的大小 SELECTtablespace_name,file_id,file_name,round( bytes / ( 1024 …...

Vue2 第一节_Vue2上手_插值表达式{{}}_访问数据和修改数据_Vue开发者工具
文章目录 1.Vue2上手-如何创建一个Vue实例,进行初始化渲染2. 插值表达式{{}}3. 访问数据和修改数据4. vue响应式5. Vue开发者工具--方便调试 1.Vue2上手-如何创建一个Vue实例,进行初始化渲染 准备容器引包创建Vue实例 new Vue()指定配置项 ->渲染数据 准备一个容器,例如: …...

华为OD机试-食堂供餐-二分法
import java.util.Arrays; import java.util.Scanner;public class DemoTest3 {public static void main(String[] args) {Scanner in new Scanner(System.in);// 注意 hasNext 和 hasNextLine 的区别while (in.hasNextLine()) { // 注意 while 处理多个 caseint a in.nextIn…...

鱼香ros docker配置镜像报错:https://registry-1.docker.io/v2/
使用鱼香ros一件安装docker时的https://registry-1.docker.io/v2/问题 一键安装指令 wget http://fishros.com/install -O fishros && . fishros出现问题:docker pull 失败 网络不同,需要使用镜像源 按照如下步骤操作 sudo vi /etc/docker/dae…...

【Oracle】分区表
个人主页:Guiat 归属专栏:Oracle 文章目录 1. 分区表基础概述1.1 分区表的概念与优势1.2 分区类型概览1.3 分区表的工作原理 2. 范围分区 (RANGE Partitioning)2.1 基础范围分区2.1.1 按日期范围分区2.1.2 按数值范围分区 2.2 间隔分区 (INTERVAL Partit…...

视频行为标注工具BehaviLabel(源码+使用介绍+Windows.Exe版本)
前言: 最近在做行为检测相关的模型,用的是时空图卷积网络(STGCN),但原有kinetic-400数据集数据质量较低,需要进行细粒度的标注,同时粗略搜了下已有开源工具基本都集中于图像分割这块,…...

GitFlow 工作模式(详解)
今天再学项目的过程中遇到使用gitflow模式管理代码,因此进行学习并且发布关于gitflow的一些思考 Git与GitFlow模式 我们在写代码的时候通常会进行网上保存,无论是github还是gittee,都是一种基于git去保存代码的形式,这样保存代码…...

在Mathematica中实现Newton-Raphson迭代的收敛时间算法(一般三次多项式)
考察一般的三次多项式,以r为参数: p[z_, r_] : z^3 (r - 1) z - r; roots[r_] : z /. Solve[p[z, r] 0, z]; 此多项式的根为: 尽管看起来这个多项式是特殊的,其实一般的三次多项式都是可以通过线性变换化为这个形式…...

mac 安装homebrew (nvm 及git)
mac 安装nvm 及git 万恶之源 mac 安装这些东西离不开Xcode。及homebrew 一、先说安装git步骤 通用: 方法一:使用 Homebrew 安装 Git(推荐) 步骤如下:打开终端(Terminal.app) 1.安装 Homebrew…...
