逻辑回归(解决分类问题)
定义:逻辑回归是一种用于解决分类问题的统计学习方法。它通过对数据进行建模,预测一个事件发生的概率。逻辑回归通常用于二元分类问题,即将数据分为两个类别。它基于线性回归模型,但使用了逻辑函数(也称为S形函数)来将输出限制在0到1之间,表示事件发生的概率。逻辑回归可以通过最大似然估计或梯度下降等方法来进行参数估计,从而得到一个可以用于分类的模型。
一、逻辑回归入门
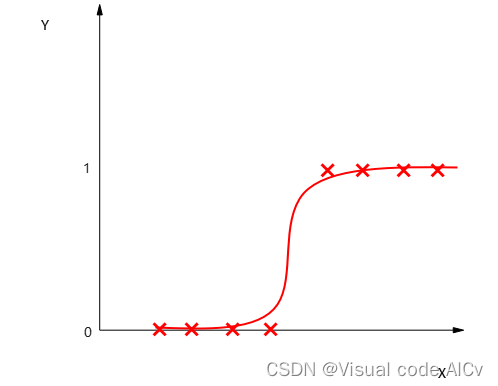
在分类肿瘤的例子中,我们将肿瘤分为恶性肿瘤和良性肿瘤。 对于恶性肿瘤赋值1(yes),对良性肿瘤赋值0(no)。并在坐标系中表示出其数据集以及对应的拟合曲线如下:

二、逻辑函数(对数几率函数)
沿用上面的例子,假设原始数据集有一个值为0.7,我们应该如何来在坐标系中表示呢? 我们需要引用一个逻辑函数来描述这些位于0~1中间的数据。
在所有的二分类问题中,我们需要将实值Z准华为0/1的值,最理想的函数肯定是分段函数(单位阶跃函数):
但是分段函数不连续,因此不能单调可微调函数转化为线性模型。所以我们希望找到一个用于替代分段函数的“近似替代函数”,希望它能够单调可微。逻辑函数(Sigmoid function)正是这样一个函数:
(1)
当我们将逻辑函数作为带入(1)式中可得:
(2)
经过变换后得到:
(3)
若将y视作样本x为正例(恶性肿瘤)的可能性,则1-y是其反比的可能性,两者的比值称为几率(odds),反映了x作为正例的相对可能性。按照通俗的话来说,我们可以视逻辑回归的输出结果为对于给定的输入x情况下输出y=1的概率。
还是以肿瘤的例子说明:其中x为肿瘤尺寸,y为良性肿瘤0和恶性肿瘤1,如果从上述(2)中得到y=0.7,则说明对于x有70%的概率为恶性肿瘤。 
逻辑函数常见形式:
三、决策边界
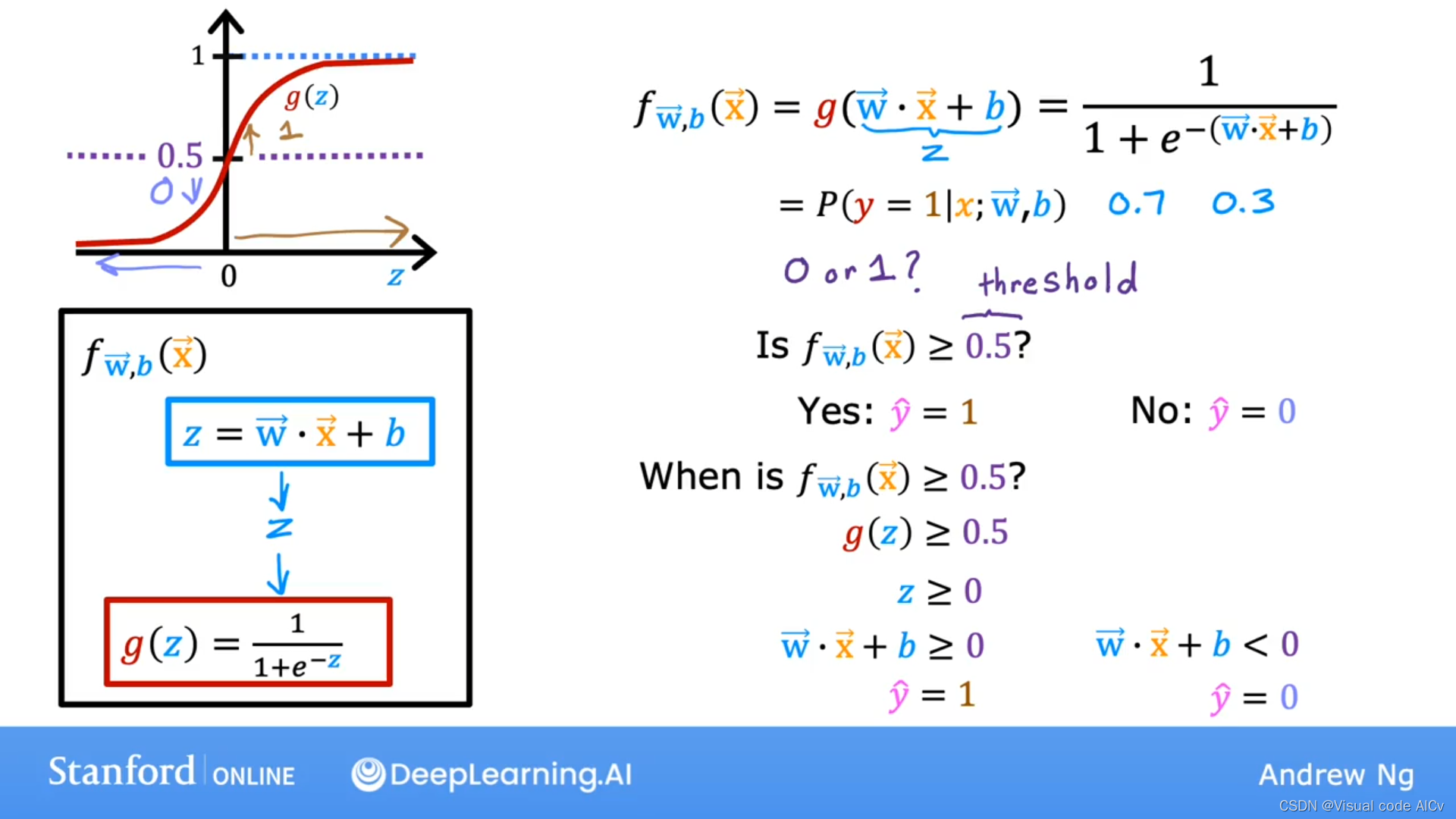
在分类问题中,通过逻辑回归得到的输出只会是确定的整数;我们必须找到一个介于0~1之间的阈值flag作为决策边界。
判断的基本形式如下:通过样本值与flag进行比较来分类;
Is
Yes:
No:
因此,我们需要确定何时的点;
有逻辑函数的基本变形形式可知在此时必有:
因此我们可以将作为决策边界
非线性的决策边界
分析决策边界的函数我们不难发现,对于非线性的决策边界我们可以综合多项式回归的知识进行求解。如下图中,使用作为决策边界。

对于多元线性回归也可以同样推导
相关文章:

逻辑回归(解决分类问题)
定义:逻辑回归是一种用于解决分类问题的统计学习方法。它通过对数据进行建模,预测一个事件发生的概率。逻辑回归通常用于二元分类问题,即将数据分为两个类别。它基于线性回归模型,但使用了逻辑函数(也称为S形函数&…...

论文阅读:Feature Refinement to Improve High Resolution Image Inpainting
项目地址:https://github.com/geomagical/lama-with-refiner 论文地址:https://arxiv.org/abs/2109.07161 发表时间:2022年6月29日 项目体验地址:https://colab.research.google.com/github/advimman/lama/blob/master/colab/LaMa…...

结构型设计模式——适配器模式
适配器模式 这个更加好理解,就是做适配功能的类,例如,现在手机没有了圆形耳机接口,只有Type-C接口,因此你如果还想要使用圆形耳机的话需要买个圆形接口转Type-C的转换器(适配器),这…...
三菱FX系列PLC定长切割控制(线缆裁切)
三菱PLC绝对定位指令DDRVA实现往复运动控制详细介绍请查看下面文章链接: https://rxxw-control.blog.csdn.net/article/details/135570157https://rxxw-control.blog.csdn.net/article/details/135570157这篇博客我们介绍线缆行业的定长切割控制相关算法。 未完待…...
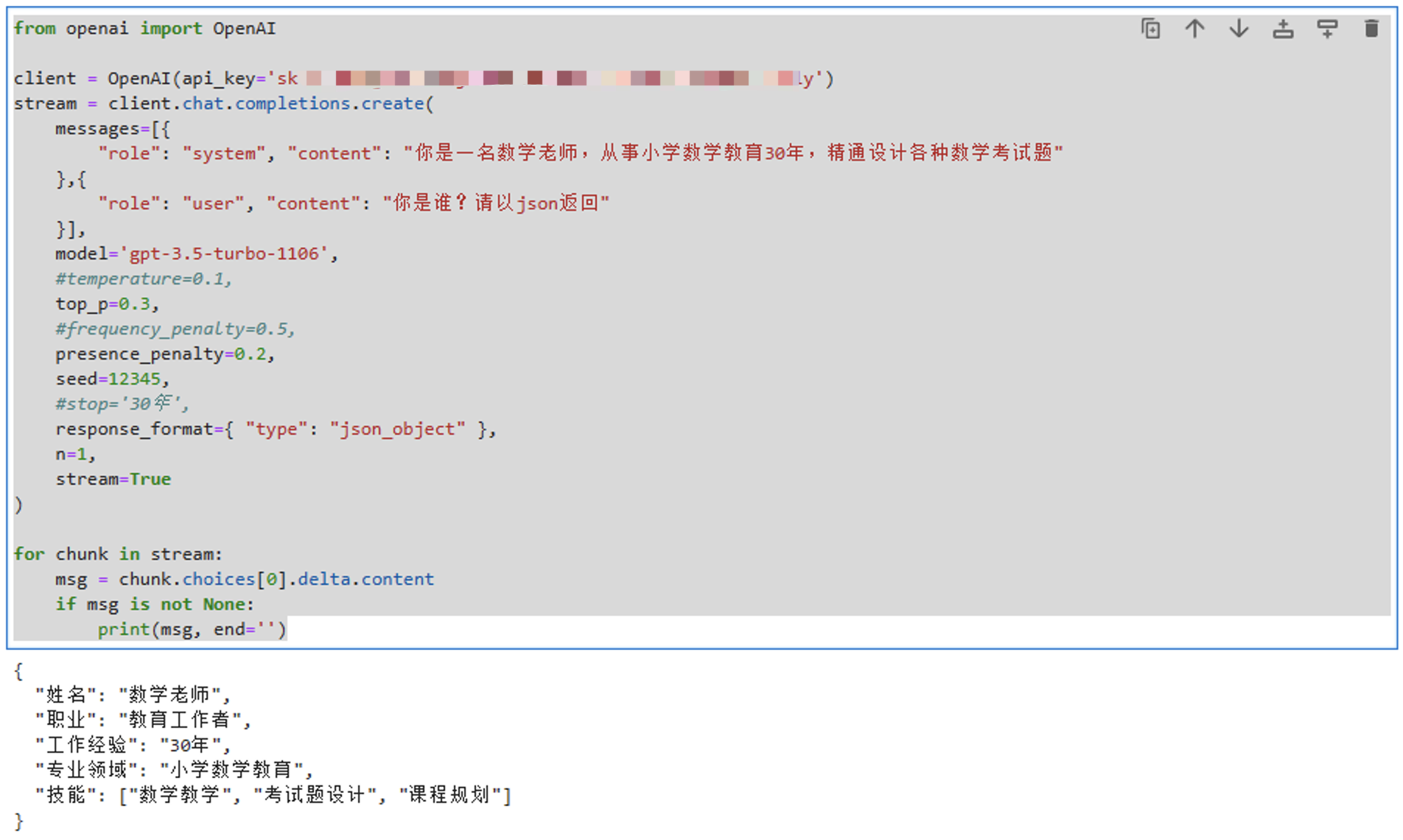
GPT编程:运行第一个聊天程序
环境搭建 很多机器学习框架和类库都是使用Python编写的,OpenAI提供的很多例子也是Python编写的,所以为了方便学习,我们这个教程也使用Python。 Python环境搭建 Python环境搭建有很多种方法,我们这里需要使用 Python 3.10 的环境…...

NLP论文阅读记录 - WOS | ROUGE-SEM:使用ROUGE结合语义更好地评估摘要
文章目录 前言0、论文摘要一、Introduction1.1目标问题1.2相关的尝试1.3本文贡献 二.相关工作三.本文方法四 实验效果4.1数据集4.2 对比模型4.3实施细节4.4评估指标4.5 实验结果4.6 细粒度分析 五 总结 前言 ROUGE-SEM: Better evaluation of summarization using ROUGE combin…...
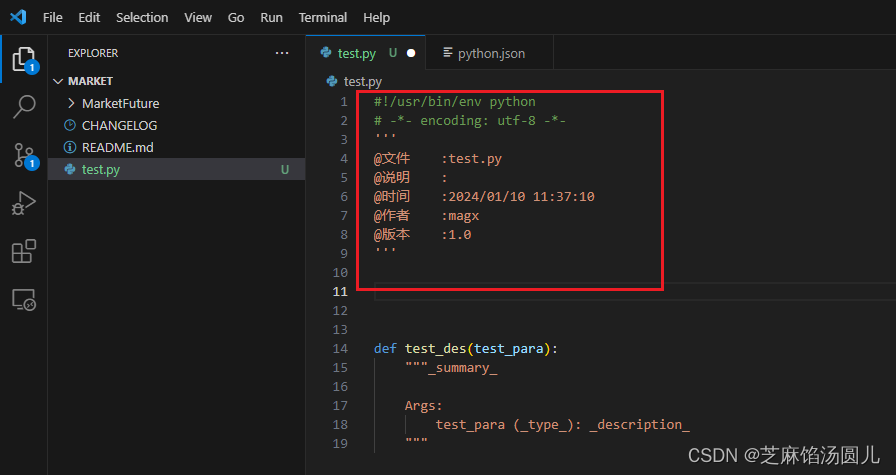
vscode 创建文件自动添加注释信息
随机记录 目录 1. 背景介绍 2. "Docstring Generator"扩展 2.1 安装 2.2 设置注释信息 3. 自动配置py 文件头注释 1. 背景介绍 在VS Code中,您可以使用扩展来为新创建的Python文件自动添加头部注释信息。有几个常用的扩展可以实现此功能࿰…...
JVM内存区域详解,一文弄懂JVM内存【内存分布、回收算法、垃圾回收器】
视频讲解地址 学习文档 一、内存区域 区域描述线程私有如何溢出程序计数器为了线程切换后能恢复到正确的执行位置,每个线程都要有一个独立的程序计数器。✅唯一一个不会内存溢出的地方虚拟机栈1. 每个方法执行的时候,Java虚拟机都会同步创建一个栈帧用于…...
uniapp搜索附近蓝牙信标(iBeacon)
一、 iBeacon介绍 iBeacon是苹果在2013年WWDC上推出一项基于蓝牙4.0(Bluetooth LE | BLE | Bluetooth Smart)的精准微定位技术,在iPhone 4S后支持。当你的手持设备靠近一个Beacon基站时,设备就能够感应到Beacon信号,范…...

Redis 常见数据结构以及使用场景分析
Java面试题目录 Redis 常见数据类型以及使用场景分析 Redis中有string、list、hash、set、sorted set、bitmap这6种数据类型。 string可以用来做缓存,分布式锁,计数器等。 list可以实现消息队列,分页查询等。 hash适合存储对象结构。 set 可…...

LMDeploy 大模型量化部署实践
LMDeploy 大模型量化部署实践 大模型部署背景模型部署定义产品形态计算设备 大模型特点大模型挑战大模型部署方案 LMDeploy简介推理性能核心功能-量化核心功能-推理引擎TurboMind核心功能 推理服务 api-server 案例(安装、部署、量化) 大模型部署背景 模型部署 定义 将训练好…...

15个为你的品牌增加曝光的维基百科推广方法-华媒舍
维基百科是全球最大的免费在线百科全书,拥有庞大的用户群体和高质量的内容。在如今竞争激烈的市场中,利用维基百科推广品牌和增加曝光度已成为许多企业的重要策略。本文将介绍15种方法,帮助你有效地利用维基百科推广品牌,提升曝光…...
启动redis出现Creating Server TCP listening socket 127.0.0.1:6379: bind: No error异常
1.进入redis安装目录,地址栏输入cmd 2.输入命令 redis-server.exe redis.windows.conf redis启动失败 解决,输入命令 #第一步 redis-cli.exe#第二步 shutdown#第三步 exit第四步 redis-server.exe redis.windows.conf 显示以下图标即成功...

响应式编程Reactor优化Callback回调地狱
1. Reactor是什么 Reactor 是一个基于Reactive Streams规范的响应式编程框架。它提供了一组用于构建异步、事件驱动、响应式应用程序的工具和库。Reactor 的核心是 Flux(表示一个包含零到多个元素的异步序列)和 Mono表示一个包含零或一个元素的异步序列…...
React项目实战--------极客园项目PC端
项目介绍:主要将学习到的项目内容进行总结(有需要项目源码的可以私信我) 关于我的项目的配置如下,请注意下载的每个版本不一样,写的api也不一样 一、项目介绍 1.资料 1)短信接收&M端演示:…...
,q(q <= 1e5)次询问,求向前走d最少要几次)
Jerry每次能向前或向后走n*n步(始终不能超过初始位置1e5),q(q <= 1e5)次询问,求向前走d最少要几次
题目 思路:因为有走的过程不能超初始位置1e5的限制,所以不能直接用奇数最多两次,4的倍数最多两次的结论。spfa,平方数的dis为1,然后推出其他数的dis #include<bits/stdc.h> using namespace std; #define int …...

【Spring Boot 3】【Flyway】数据库版本管理
【Spring Boot 3】【Flyway】数据库版本管理 背景介绍开发环境开发步骤及源码工程目录结构总结背景 软件开发是一门实践性科学,对大多数人来说,学习一种新技术不是一开始就去深究其原理,而是先从做出一个可工作的DEMO入手。但在我个人学习和工作经历中,每次学习新技术总是…...
)
蓝桥杯基础数据结构(java版)
引言 数据结构数据结构。所以数据结构是一个抽象的概念。其目的是为了更好的组织数据方便数据存储。下面我们来看一些简单的数据储存方式 输入和输出 这里先介绍java的输入和输出。简单引入,不过多详细介绍,等我单一写一篇的时候这里会挂上链接 简单的…...

39 C++ 模版中的参数如果 是 vector,list等集合类型如何处理呢?
在前面写的例子中,模版参数一般都是 int,或者一个类Teacher,假设我们现在有个需求:模版的参数要是vector,list这种结合类型应该怎么写呢? //当模版中的类型是 vector ,list 等集合类型的时候的处…...
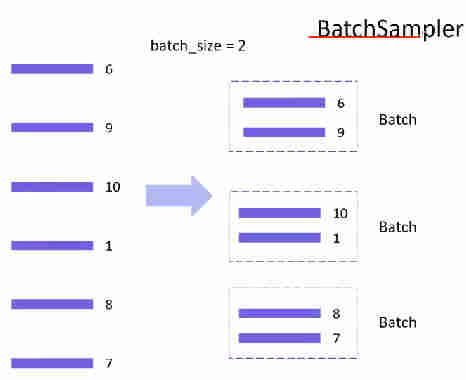
5.Pytorch模型单机多GPU训练原理与实现
文章目录 Pytorch的单机多GPU训练1)多GPU训练介绍2)pytorch中使用单机多GPU训练DistributedDataParallel(DDP)相关变量及含义a)初始化b)数据准备c)模型准备d)清理e)运行 3)使用DistributedDataParallel训练模型的一个简单实例 欢迎访问个人网络日志🌹🌹知…...

铭豹扩展坞 USB转网口 突然无法识别解决方法
当 USB 转网口扩展坞在一台笔记本上无法识别,但在其他电脑上正常工作时,问题通常出在笔记本自身或其与扩展坞的兼容性上。以下是系统化的定位思路和排查步骤,帮助你快速找到故障原因: 背景: 一个M-pard(铭豹)扩展坞的网卡突然无法识别了,扩展出来的三个USB接口正常。…...

第19节 Node.js Express 框架
Express 是一个为Node.js设计的web开发框架,它基于nodejs平台。 Express 简介 Express是一个简洁而灵活的node.js Web应用框架, 提供了一系列强大特性帮助你创建各种Web应用,和丰富的HTTP工具。 使用Express可以快速地搭建一个完整功能的网站。 Expre…...

DockerHub与私有镜像仓库在容器化中的应用与管理
哈喽,大家好,我是左手python! Docker Hub的应用与管理 Docker Hub的基本概念与使用方法 Docker Hub是Docker官方提供的一个公共镜像仓库,用户可以在其中找到各种操作系统、软件和应用的镜像。开发者可以通过Docker Hub轻松获取所…...

测试markdown--肇兴
day1: 1、去程:7:04 --11:32高铁 高铁右转上售票大厅2楼,穿过候车厅下一楼,上大巴车 ¥10/人 **2、到达:**12点多到达寨子,买门票,美团/抖音:¥78人 3、中饭&a…...
)
GitHub 趋势日报 (2025年06月08日)
📊 由 TrendForge 系统生成 | 🌐 https://trendforge.devlive.org/ 🌐 本日报中的项目描述已自动翻译为中文 📈 今日获星趋势图 今日获星趋势图 884 cognee 566 dify 414 HumanSystemOptimization 414 omni-tools 321 note-gen …...

SpringTask-03.入门案例
一.入门案例 启动类: package com.sky;import lombok.extern.slf4j.Slf4j; import org.springframework.boot.SpringApplication; import org.springframework.boot.autoconfigure.SpringBootApplication; import org.springframework.cache.annotation.EnableCach…...

【笔记】WSL 中 Rust 安装与测试完整记录
#工作记录 WSL 中 Rust 安装与测试完整记录 1. 运行环境 系统:Ubuntu 24.04 LTS (WSL2)架构:x86_64 (GNU/Linux)Rust 版本:rustc 1.87.0 (2025-05-09)Cargo 版本:cargo 1.87.0 (2025-05-06) 2. 安装 Rust 2.1 使用 Rust 官方安…...

在 Visual Studio Code 中使用驭码 CodeRider 提升开发效率:以冒泡排序为例
目录 前言1 插件安装与配置1.1 安装驭码 CodeRider1.2 初始配置建议 2 示例代码:冒泡排序3 驭码 CodeRider 功能详解3.1 功能概览3.2 代码解释功能3.3 自动注释生成3.4 逻辑修改功能3.5 单元测试自动生成3.6 代码优化建议 4 驭码的实际应用建议5 常见问题与解决建议…...

倒装芯片凸点成型工艺
UBM(Under Bump Metallization)与Bump(焊球)形成工艺流程。我们可以将整张流程图分为三大阶段来理解: 🔧 一、UBM(Under Bump Metallization)工艺流程(黄色区域ÿ…...

门静脉高压——表现
一、门静脉高压表现 00:01 1. 门静脉构成 00:13 组成结构:由肠系膜上静脉和脾静脉汇合构成,是肝脏血液供应的主要来源。淤血后果:门静脉淤血会同时导致脾静脉和肠系膜上静脉淤血,引发后续系列症状。 2. 脾大和脾功能亢进 00:46 …...
