AnnData:单细胞和空间组学分析的数据基石
AnnData:单细胞和空间组学分析的数据基石
今天我们来系统学习一下单细胞分析的标准数据类型——AnnData!
AnnData就是有注释的数据,全称是Annotated Data。
AnnData是为了矩阵类型数据设计的,也就是长得和表格一样的数据。比如说我们有 n n n个样本(观测值),每个样本用一个 d d d维的向量表示,这个向量的每一个维度表示着一个特征。也就是说,这是一个 n × d n \times d n×d的矩阵。
举个例子,在scRNA-seq数据中,每一行表示一个带有barcode的细胞,每一列表示带有gene id的基因。而且数据还不只这一个矩阵,每个细胞和基因可能会有额外的信息(metadata),比如:①细胞的来源;②基因是否甲基化等等。此外还有一些非结构化的metadata,比如画图用的一些参数(调色板等)。
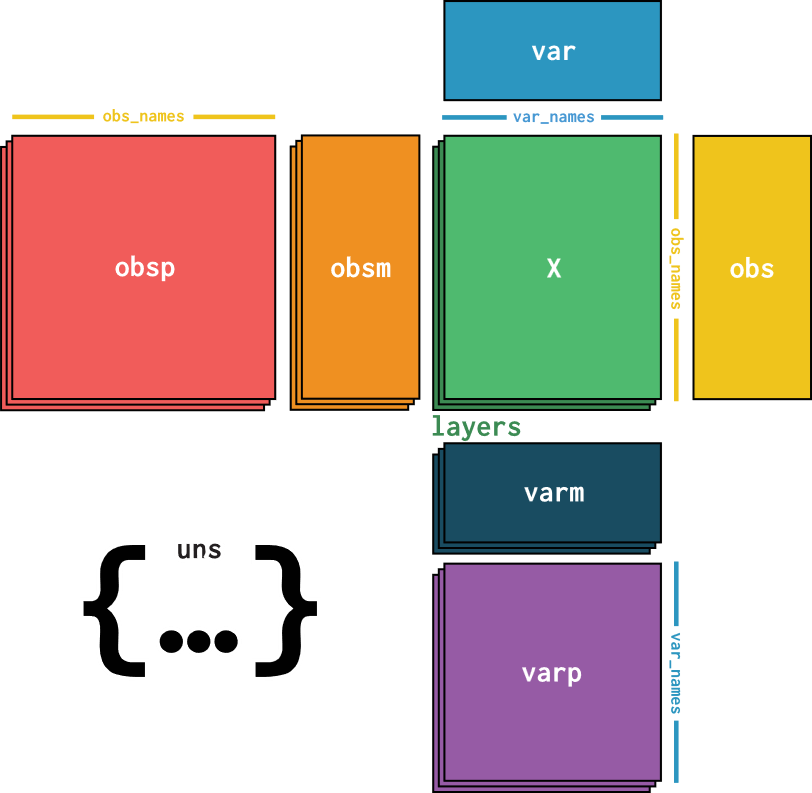
目前来说,似乎除了AnnData,没有其他的数据结构可以做到:
- 处理稀疏性
- 处理非结构化的数据
- 处理样本和特征的metadata
- 容易上手
AnnData的论文也发在了nature biotechnology上!

安装与导入
# !pip install anndata
import numpy as np
import pandas as pd
import anndata as ad
from scipy.sparse import csr_matrix
print(ad.__version__)
0.10.4
初始化AnnData
我们来创建一个AnnData对象吧,首先我们通过NumPy随机生成一些数据,然后再用csr_matrix()转换成稀疏矩阵。
我们生成的数据是一个大小为100*2000数据符合泊松分布的矩阵,可以假装是100个细胞和2000个基因的counts矩阵。
泊松分布(Poisson distribution)是一种离散概率分布,它用于表示在固定时间或空间区间内发生某事件的概率,假设这些事件以已知的恒定平均速率独立发生。泊松分布通常用于模拟那些发生次数较少但有大量独立机会发生的事件。
我们使用泊松分布生成随机数可能是因为我们想模拟一个细胞的基因表达,而这其实也算以某个固定的平均速率发生,而且每个事件的发生是差不多独立的。
泊松分布适合于模拟生物学实验中的计数数据,如RNA测序中每个基因的counts,因为这些counts可以看作是在固定时间内发生的事件数量。
λ=1,代表着事件发生的平均次数是1,这样会比较稀疏
counts = csr_matrix(np.random.poisson(1, size=(100, 2000)), dtype=np.float32)
# 使用NumPy库生成一个形状为100x2000的数组,数组中的每个元素都是从参数为1的泊松分布中随机抽取的数值。
# 将上述生成的数组转换为压缩稀疏行(CSR)格式的稀疏矩阵。
# CSR格式是一种高效存储和操作稀疏矩阵的方式,特别是当矩阵中大部分元素为零时。
adata = ad.AnnData(counts)
# 创建了一个AnnData对象,它是anndata库中的一个核心数据结构,用于存储带注释的多维数据。
# 在这里,counts稀疏矩阵被用作AnnData对象的主数据矩阵X。
adata
AnnData object with n_obs × n_vars = 100 × 2000
上面的输出是总结了一下样本和特征有多少,如果想看我们的数据就可以通过adata.X。
adata.X
<100x2000 sparse matrix of type '<class 'numpy.float32'>'with 125993 stored elements in Compressed Sparse Row format>
现在我们来设置一下样本和特征的名字,这也算是建立索引的步骤。
# 设置观测值名称,每个名称格式为"Cell_序号"
adata.obs_names = [f"Cell_{i:d}" for i in range(adata.n_obs)]
# 使用列表推导式创建了一个新的列表,列表中的每个元素都是以"Cell_"开头,后面跟着一个整数序号的字符串。
# 这个序号从0开始,一直到adata.n_obs(观测值的数量)减1。
adata.var_names = [f"Gene_{i:d}" for i in range(adata.n_vars)]
print(adata.obs_names[:10])
Index(['Cell_0', 'Cell_1', 'Cell_2', 'Cell_3', 'Cell_4', 'Cell_5', 'Cell_6','Cell_7', 'Cell_8', 'Cell_9'],dtype='object')
取子集
这么多数据,我们一般会关注自己想要的,索引方式非常方便。直接用列表把样本和特征的名字一放就行。
adata[["Cell_1", "Cell_10"], ["Gene_5", "Gene_1900"]]
View of AnnData object with n_obs × n_vars = 2 × 2
加点额外的metadata
样本/特征
细胞有类别、基因也不仅仅只有counts,怎么加额外的特征呢?这也很简单,就搞一个和样本或者特征一样长的向量赋值即可。
So we have the core of our object and now we’d like to add metadata at both the observation and variable levels. This is pretty simple with AnnData, both adata.obs and adata.var are Pandas DataFrames.
ct = np.random.choice(["B", "T", "Monocyte"], size=(adata.n_obs,))
adata.obs["cell_type"] = pd.Categorical(ct) # Categoricals are preferred for efficiency
adata.obs
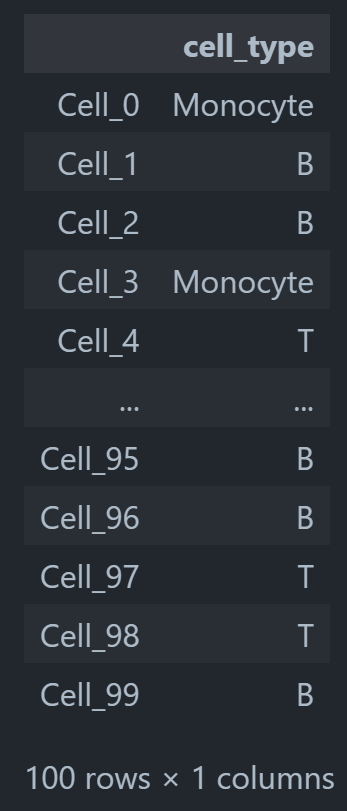
我们可以发现,我们的数据描述也变了,多了一个obs: 'cell_type',这也就是我们刚刚定义的细胞类型。
adata
AnnData object with n_obs × n_vars = 100 × 2000obs: 'cell_type'
通过metadata取子集
我们可以用我们刚刚为细胞加的特征cell_type来选择我们想要的数据,比如我们想要所有B细胞的数据。
bdata = adata[adata.obs.cell_type == "B"]
bdata
View of AnnData object with n_obs × n_vars = 36 × 2000obs: 'cell_type'
样本和特征水平的多维度metadata(矩阵)
我们有时候想加的metadata不是一个向量能描述的,它可能是个矩阵。比如细胞的UMAP降维结果,降到2维就是一个细胞个数*2维的矩阵。这时候我们就可以用obsm或者varm来添加就行。
adata.obsm["X_umap"] = np.random.normal(0, 1, size=(adata.n_obs, 2))
# 生成一个100*2的正态分布随机数矩阵
adata.varm["gene_stuff"] = np.random.normal(0, 1, size=(adata.n_vars, 5))
adata.obsm
AxisArrays with keys: X_umap
再看看我们的adata,又更新了。
adata
AnnData object with n_obs × n_vars = 100 × 2000obs: 'cell_type'obsm: 'X_umap'varm: 'gene_stuff'
关于.obsm/.varm的额外说明:
- .obsm和.varm可以存储来自不同来源的矩阵。这些数据可以是Pandas DataFrame、scipy稀疏矩阵或numpy数组。也就是说,我们可以将这些不同类型的数据结构直接存储在.obsm或.varm中,而无需进行转换。
- 当使用scanpy进行单细胞分析时,.obsm和.varm中的值(列)不容易直接用于绘图。相比之下,.obs中的项可以更容易地被绘制在UMAP等降维图上。例如,如果我们有UMAP坐标存储在.obsm中,我们可能需要将它们转移到.obs中,以便使用scanpy的绘图功能。
非结构化的metadata
非结构化,就是随便什么数据都行,不管是列表、字典还是什么其他的,只要是对于我们数据分析有用的都可以放进来,就放在.uns里面就行。
adata.uns["random"] = [1, 2, 3]
adata.uns
OrderedDict([('random', [1, 2, 3])])
adata
AnnData object with n_obs × n_vars = 100 × 2000obs: 'cell_type'obsm: 'X_umap'varm: 'gene_stuff'
欸,非结构化metadata的就没有直接显示。
Layers
最后得说一下layers,这个非常有用。我们经常会对原始数据进行处理,比如标准化、对数化等等。这些可以转换后的数据可以存储在layer中。
adata.layers["log_transformed"] = np.log1p(adata.X)
adata
AnnData object with n_obs × n_vars = 100 × 2000obs: 'cell_type'uns: 'random'obsm: 'X_umap'varm: 'gene_stuff'layers: 'log_transformed'
还原回DataFrames
直接使用.to_df()即可,还可以指定layer。
adata.to_df(layer="log_transformed")

你看,dataframe的行列索引也都是我们的.obs_names/.var_names。
保存结果
AnnData提供了一种基于HDF5的持久化文件格式:h5ad。这种格式专门设计用于存储AnnData对象,使得数据可以高效地被读取和写入。
当AnnData对象中有包含少量类别的字符串列时,如果这些字符串列还没有被转换为分类数据类型(categoricals),AnnData会自动将它们转换为分类数据类型。分类数据类型是pandas库中的一种数据类型,用于表示具有固定数量类别的变量,这种类型在内存使用和性能上比普通字符串类型更优。
例如,如果我们有一列,全是字符串,它只包含几个不同的值(如"yes"和"no"),AnnData会自动将这个列的数据类型转换为分类数据类型,这样可以提高数据处理的效率和速度。
adata.write('my_results.h5ad', compression="gzip")
!ls -lh | grep my_results.h5ad
-rw-rw-r-- 1 659K Jan 14 15:31 my_results.h5ad
结语
这次只是学习了AnnData最基础的知识,之后会介绍AnnData进阶的操作。
参考资料:Getting started with anndata — anndata 0.11.0.dev46+g0219fef documentation
如果觉得还不错,记得点赞+收藏哟!谢谢大家的阅读!( ̄︶ ̄)↗
相关文章:

AnnData:单细胞和空间组学分析的数据基石
AnnData:单细胞和空间组学分析的数据基石 今天我们来系统学习一下单细胞分析的标准数据类型——AnnData! AnnData就是有注释的数据,全称是Annotated Data。 AnnData是为了矩阵类型数据设计的,也就是长得和表格一样的数据。比如…...

C语言中的 `string.h` 头文件包含的函数
C语言中的 string.h 头文件包含了许多与字符串或数字相关的函数。这些函数可以用于字符串的复制、连接、搜索、比较等操作。 常用字符串函数 函数名功能strlen()返回字符串的长度strcpy()将一个字符串复制到另一个字符串中strncpy()将最多 n 个字符从一个字符串复制到另一个字…...

kotlin的抽象类和抽象方法
在 Kotlin 中,抽象类和抽象方法是面向对象编程中的概念,用于实现抽象和多态性。抽象类无法实例化,这意味着我们无法创建抽象类的对象。与其他类不同,抽象类总是打开的,因此我们不需要使用open关键字。 抽象类ÿ…...
)
2022年面经记录(base杭州)
duandian科技(笔试未通过) 笔试题:leetCode热题第20题有效的括号 面后感:没怎么刷算法题,js 基础不扎实 laiweilai(三面未通过) 一面:笔试题 写一个函数,获取url中的指定…...

安装Docker图形管理界面portainer
安装Docker图形管理界面portainer 映射data文件夹根据自己环境更换 docker run -d --name portainer -p 9000:9000 -v /var/run/docker.sock:/var/run/docker.sock -v /yourpath/docker/portainer:/data --restartalways portainer/portainer-ce:latest好好享受吧!…...

Linux学习记录——사십 高级IO(1)
文章目录 1、IO2、同、异步IO(5种IO类型)3、其它高级IO4、非阻塞IO 其它IO类型的实现在这篇之后的三篇 1、IO input,output。调用read或recv接口时,如果对方长时间不向我方接收缓冲区拷贝数据,我们的进程就只能阻塞&a…...

【代码随想录】2
数组篇 二分查找 int search(int* nums, int numsSize, int target) { int left0; int rightnumsSize-1; while(left<right) {int mlddle(leftright)/2;if(nums[mlddle]>target){rightmlddle-1;}else if(nums[mlddle]<target){leftmlddle1;}else{return mlddle;}} r…...

TCP性能分析
ref: TCP性能和发送接收窗口、Buffer的关系 | plantegg...
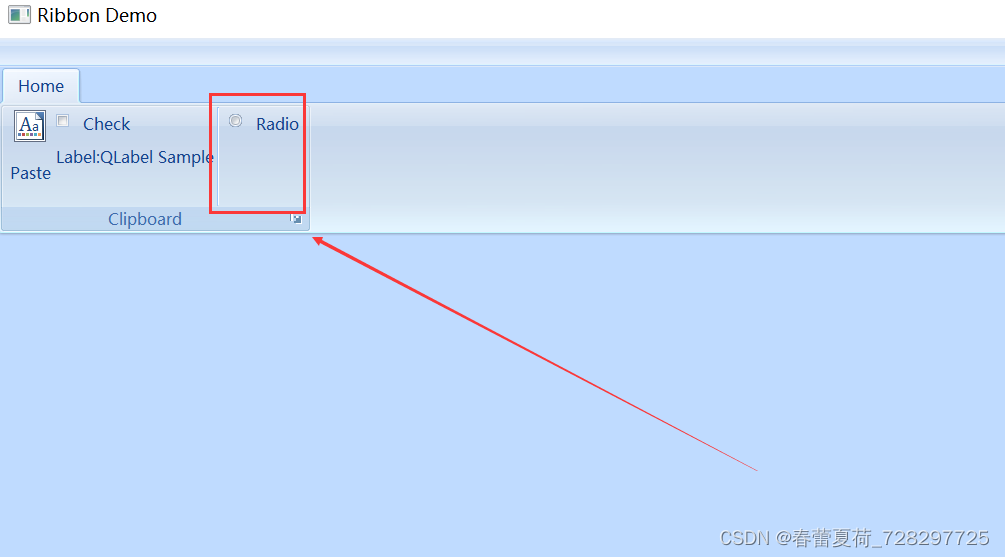
RibbonGroup 添加QRadioButton
RibbonGroup添加QRadioButton: QRadioButton * pRadio new QRadioButton(tr("Radio")); pRadio->setToolTip(tr("Radio")); groupClipboard->addWidget(pRadio); connect(pRadio, SIGNAL(clicked(…...

一篇文章掌握WebService服务、工作原理、核心组件、主流框架
目录 1、WebService定义 解决问题: 2、WebService的工作原理 2.1 实现一个完整的Web服务包括以下步骤 2.2 调用方式 3、Web Service的核心组件 3.1 XML 3.2 SOAP 3.3 WSDL 3.4 UDDI 4、主流框架 4.1 AXIS(已淘汰) 4.2 XFire 4.3 CXF 5、Soap协议详解…...

观成科技-加密C2框架EvilOSX流量分析
工具简介 EvilOSX是一款开源的,由python编写专门为macOS系统设计的C2工具,该工具可以利用自身释放的木马来实现一系列集成功能,如键盘记录、文件捕获、浏览器历史记录爬取、截屏等。EvilOSX主要使用HTTP协议进行通信,通信内容为特…...

PCL 计算异面直线的距离
目录 一、算法原理二、代码实现三、结果展示四、相关链接本文由CSDN点云侠原创,PCL 计算异面直线的距离,爬虫自重。如果你不是在点云侠的博客中看到该文章,那么此处便是不要脸的爬虫与GPT。 一、算法原理 设置直线 A B AB A...
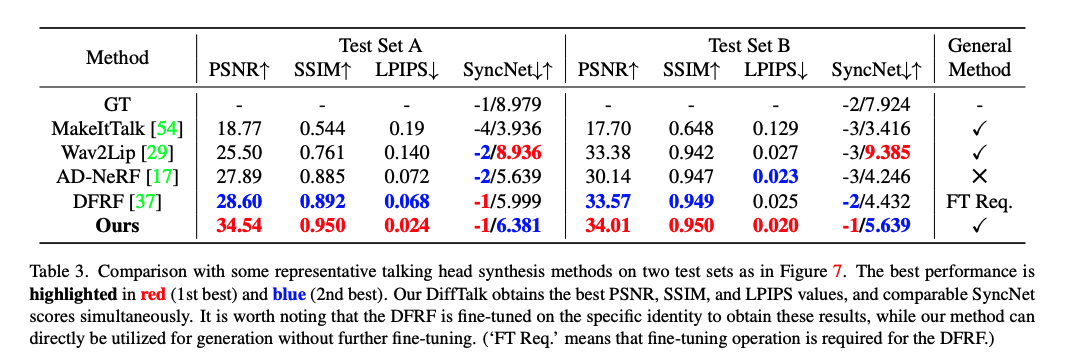
【数字人】9、DiffTalk | 使用扩散模型基于 audio-driven+对应人物视频 合成说话头(CVPR2023)
论文:DiffTalk: Crafting Diffusion Models for Generalized Audio-Driven Portraits Animation 代码:https://sstzal.github.io/DiffTalk/ 出处:CVPR2023 特点:需要音频对应人物的视频来合成新的说话头视频,嘴部抖…...
完成源示例
本主题演示如何创作和使用自己的完成源类,类似于 .NET 的 TaskCompletionSource。 completion_source 示例的源代码 下面的列表中的代码作为示例提供。 其目的是说明如何编写自己的版本。 例如,支持取消和错误传播不在此示例的范围内。 #include <w…...

业务和流程的关系
背景 概念不清,沟通就容易出现问题,最可怕会出现跑偏情况如何解决,数字化落地过程,程序是死的,最怕灵活,所以在沟通和编码,设计中,很重要的一点就是解决概念,澄清问题&a…...
【河海大学论文LaTeX+VSCode全指南】
河海大学论文LaTeXVSCode全指南 前言一、 LaTeX \LaTeX{} LATEX的安装二、VScode的安装三、VScode的配置四、验证五、优化 前言 LaTeX \LaTeX{} LATEX在论文写作方面具有传统Word无法比拟的优点,VScode作为一个轻量化的全功能文本编辑器,由于其极强的…...

学习python仅此一篇就够了(文件操作:读,写,追加)
python文件操作 文件编码 编码技术即:翻译的规则,记录了如何将内容翻译成二进制,以及如何将二进制翻译回可识别内容。 计算机中有许多可用编码: UTF-8 GBK BUG5 文件的读取操作 open()函数 在pyth…...

vue中 ref 和 $refs的使用
1. 作用 利用 ref 和 $refs 可以用于 获取 dom 元素, 或 组件实例 2. 获取 dom 使用步骤: 2.1 目标标签添加属性 :ref <div ref"chartRef">我是渲染图表的容器</div>2.2 通过$ref:获取标签 mounted() {console.log(this.$re…...

Centos7升级openssl到openssl1.1.1
Centos7升级openssl到openssl1.1.1 1、先查看openssl版本:openssl version 2、Centos7升级openssl到openssl1.1.1 升级步骤 #1、更新所有现有的软件包列表并安装最新的软件包: $sudo yum update #2、接下来,我们需要从源代码编译和构建OpenS…...
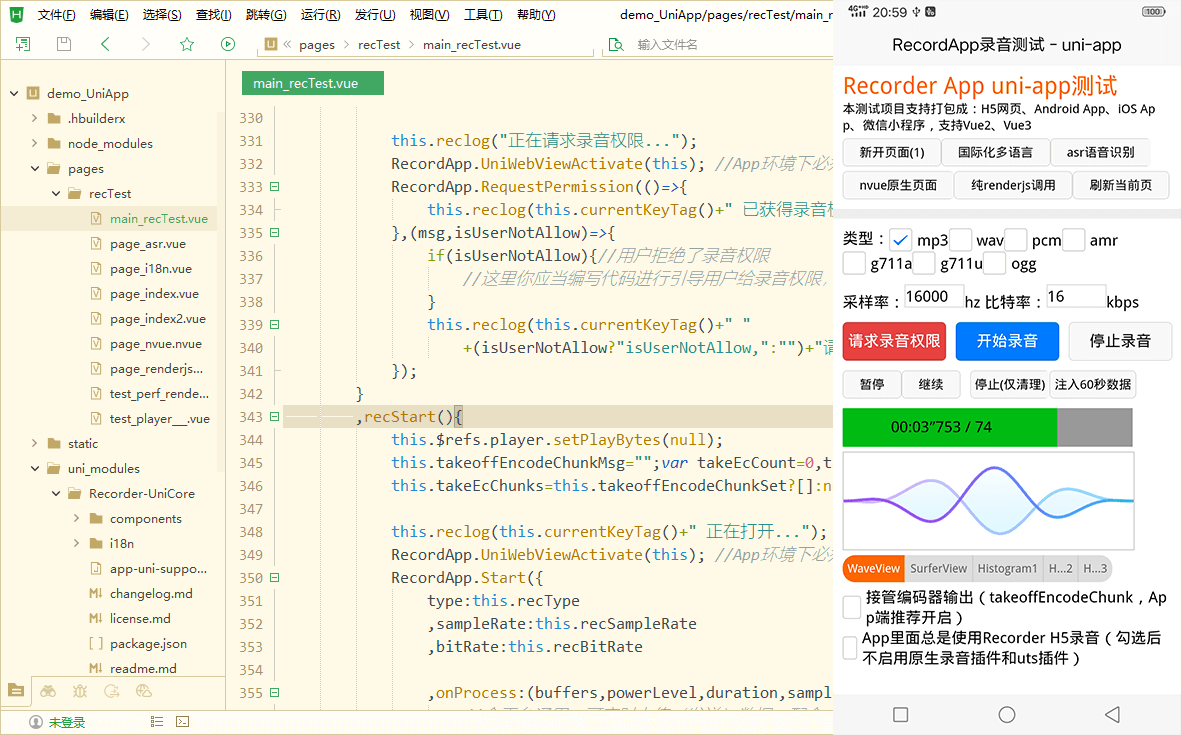
uniapp中实现H5录音和上传、实时语音识别(兼容App小程序)和波形可视化
文章目录 Recorder-UniCore插件特性集成到项目中调用录音上传录音ASR语音识别 在uniapp中使用Recorder-UniCore插件可以实现跨平台录音功能,uniapp自带的recorderManager接口不支持H5、录音格式和实时回调onFrameRecorded兼容性不好,用Recorder插件可避免…...

零门槛NAS搭建:WinNAS如何让普通电脑秒变私有云?
一、核心优势:专为Windows用户设计的极简NAS WinNAS由深圳耘想存储科技开发,是一款收费低廉但功能全面的Windows NAS工具,主打“无学习成本部署” 。与其他NAS软件相比,其优势在于: 无需硬件改造:将任意W…...

(十)学生端搭建
本次旨在将之前的已完成的部分功能进行拼装到学生端,同时完善学生端的构建。本次工作主要包括: 1.学生端整体界面布局 2.模拟考场与部分个人画像流程的串联 3.整体学生端逻辑 一、学生端 在主界面可以选择自己的用户角色 选择学生则进入学生登录界面…...

基于服务器使用 apt 安装、配置 Nginx
🧾 一、查看可安装的 Nginx 版本 首先,你可以运行以下命令查看可用版本: apt-cache madison nginx-core输出示例: nginx-core | 1.18.0-6ubuntu14.6 | http://archive.ubuntu.com/ubuntu focal-updates/main amd64 Packages ng…...

Linux相关概念和易错知识点(42)(TCP的连接管理、可靠性、面临复杂网络的处理)
目录 1.TCP的连接管理机制(1)三次握手①握手过程②对握手过程的理解 (2)四次挥手(3)握手和挥手的触发(4)状态切换①挥手过程中状态的切换②握手过程中状态的切换 2.TCP的可靠性&…...

NFT模式:数字资产确权与链游经济系统构建
NFT模式:数字资产确权与链游经济系统构建 ——从技术架构到可持续生态的范式革命 一、确权技术革新:构建可信数字资产基石 1. 区块链底层架构的进化 跨链互操作协议:基于LayerZero协议实现以太坊、Solana等公链资产互通,通过零知…...

k8s业务程序联调工具-KtConnect
概述 原理 工具作用是建立了一个从本地到集群的单向VPN,根据VPN原理,打通两个内网必然需要借助一个公共中继节点,ktconnect工具巧妙的利用k8s原生的portforward能力,简化了建立连接的过程,apiserver间接起到了中继节…...

Fabric V2.5 通用溯源系统——增加图片上传与下载功能
fabric-trace项目在发布一年后,部署量已突破1000次,为支持更多场景,现新增支持图片信息上链,本文对图片上传、下载功能代码进行梳理,包含智能合约、后端、前端部分。 一、智能合约修改 为了增加图片信息上链溯源,需要对底层数据结构进行修改,在此对智能合约中的农产品数…...

Java + Spring Boot + Mybatis 实现批量插入
在 Java 中使用 Spring Boot 和 MyBatis 实现批量插入可以通过以下步骤完成。这里提供两种常用方法:使用 MyBatis 的 <foreach> 标签和批处理模式(ExecutorType.BATCH)。 方法一:使用 XML 的 <foreach> 标签ÿ…...

JVM虚拟机:内存结构、垃圾回收、性能优化
1、JVM虚拟机的简介 Java 虚拟机(Java Virtual Machine 简称:JVM)是运行所有 Java 程序的抽象计算机,是 Java 语言的运行环境,实现了 Java 程序的跨平台特性。JVM 屏蔽了与具体操作系统平台相关的信息,使得 Java 程序只需生成在 JVM 上运行的目标代码(字节码),就可以…...

根目录0xa0属性对应的Ntfs!_SCB中的FileObject是什么时候被建立的----NTFS源代码分析--重要
根目录0xa0属性对应的Ntfs!_SCB中的FileObject是什么时候被建立的 第一部分: 0: kd> g Breakpoint 9 hit Ntfs!ReadIndexBuffer: f7173886 55 push ebp 0: kd> kc # 00 Ntfs!ReadIndexBuffer 01 Ntfs!FindFirstIndexEntry 02 Ntfs!NtfsUpda…...
