奇异值分解在图形压缩中的应用
奇异值分解在图形压缩中的应用
在研究奇异值分解的工程应用之前,我们得明白什么是奇异值?什么是奇异向量?
奇异值与奇异向量
概念:奇异值描述了矩阵在一组特定向量上的行为,奇异向量描述了其最大的作用方向。
奇异值分解(SVD)
矩阵A的分解涉及一个 m × n m \times n m×n的矩阵 Σ \Sigma Σ,其中 Σ \Sigma Σ= [ D 0 0 0 ] \begin{bmatrix} D &0\\0&0\end{bmatrix} [D000],D是一个 r × r r\times r r×r的方阵 ( r ≤ m , r ≤ n ) ( r \leq m , r\leq n) (r≤m,r≤n)
定理:设A是秩为 r r r的 m × n m\times n m×n的矩阵,那么存在一个类似于 Σ \Sigma Σ的矩阵,其中 D D D的对角线元素是 A A A的前 r r r个奇异值, σ 1 ≥ σ 2 ≥ σ 3 ≥ . . . ≥ σ r > 0 \sigma_1 \geq\sigma_2 \geq\sigma_3 \geq... \geq\sigma_r>0 σ1≥σ2≥σ3≥...≥σr>0并且存在一个 m × m m\times m m×m的正交矩阵 U U U 和一个 n × n n\times n n×n的正交矩阵 V T V^T VT使得 A = U Σ V T A=U\Sigma V^T A=UΣVT
奇异值分解计算过程
我们先假设一个矩阵 A = [ 2 3 0 2 ] A = \begin{bmatrix} 2 & 3 \\ \ 0 & 2\end{bmatrix} A=[2 032]
设 U = [ u 1 u 2 u 3 . . . ] U=[u_1 u_2 u_3 ...] U=[u1u2u3...] , ∑ = d i a g [ σ 1 σ 2 σ 3 . . . ] \sum = diag[\sigma_1 \sigma_2 \sigma_3 ...] ∑=diag[σ1σ2σ3...] , V = [ v 1 v 2 v 3 . . . ] T V=\begin{bmatrix} v_1 \\ v_2\\ v_3 \\ ...\end{bmatrix}^T V= v1v2v3... T
其中 U U U代表A的正交矩阵; ∑ \sum ∑代表A的由奇异值组成的左奇异向量矩阵; V V V代表A的右奇异向量矩阵。
求A的 U , ∑ , V U , \sum , V U,∑,V.
- 计算 A T A A^TA ATA
A T A = [ 2 0 3 2 ] [ 2 3 0 2 ] = [ 13 6 6 4 ] A^TA =\begin{bmatrix} 2&0\\3&2 \end{bmatrix} \begin{bmatrix} 2&3\\0&2\end{bmatrix}= \begin{bmatrix} 13&6\\6&4 \end{bmatrix} ATA=[2302][2032]=[13664] - 计算 A T A A^TA ATA的奇异值 σ \sigma σ
σ 1 2 σ 2 2 = d e t A T A = 16 σ 1 2 + σ 2 2 = t r A T A = 17 ∴ σ 1 2 = 16 , σ 2 2 = 1 ∴ σ 1 = 4 , σ 2 = 1 ∴ Σ = [ 4 0 0 1 ] \sigma_1^2\sigma_2^2 = det A^TA = 16 \\ \sigma_1^2 + \sigma_2^2 = tr A^TA = 17 \\ \therefore \sigma_1^2 =16, \sigma_2^2= 1\\ \therefore \sigma_1 =4, \sigma_2= 1\\ \therefore \Sigma=\begin{bmatrix} 4&0\\0&1 \end{bmatrix} σ12σ22=detATA=16σ12+σ22=trATA=17∴σ12=16,σ22=1∴σ1=4,σ2=1∴Σ=[4001] - 将 σ 1 , σ 2 \sigma_1,\sigma_2 σ1,σ2带入 A T A A^TA ATA中求其特征向量
v 1 = [ 1 5 2 5 ] , v 2 = [ − 2 5 1 5 ] ∴ V = [ 1 5 − 2 5 2 5 1 5 ] \\ v_1= \begin{bmatrix} \frac{1}{\sqrt5} \\\\ \frac{2}{\sqrt5} \end{bmatrix} , v_2= \begin{bmatrix} -\frac{2}{\sqrt5}\\\\\frac{1}{\sqrt5} \end{bmatrix} \\\therefore V= \begin{bmatrix} \frac{1}{\sqrt5}&-\frac{2}{\sqrt5} \\\\ \frac{2}{\sqrt5}&\frac{1}{\sqrt5}\end{bmatrix} v1= 5152 ,v2= −5251 ∴V= 5152−5251 - 构造标准正交向量
u i = 1 σ i A v i ∴ u 1 = 1 σ 1 A v 1 = 1 4 [ 2 3 0 2 ] [ 1 5 2 5 ] = [ 2 5 1 5 ] ∴ u 2 = 1 σ 2 A v 2 = 1 1 [ 2 3 0 2 ] [ − 2 5 1 5 ] = [ − 1 5 2 5 ] ∴ U = ( u 1 , u 2 ) = [ 2 5 − 1 5 1 5 2 5 ] u_i=\frac{1}{\sigma_i}Av_i \\ \therefore u_1=\frac{1}{\sigma_1}Av_1=\frac{1}{4}\begin{bmatrix} 2&3\\\\0&2\end {bmatrix} \begin{bmatrix} \frac{1}{\sqrt5} \\\\ \frac{2}{\sqrt5} \end{bmatrix} =\begin{bmatrix} \frac{2}{\sqrt5}\\ \\ \frac{1}{\sqrt5} \end {bmatrix} \\ \therefore u_2=\frac{1}{\sigma_2}Av_2=\frac{1}{1}\begin{bmatrix} 2&3\\\\0&2\end {bmatrix} \begin{bmatrix} - \frac{2}{\sqrt5} \\\\ \frac{1}{\sqrt5} \end{bmatrix} =\begin{bmatrix} -\frac{1}{\sqrt5}\\ \\ \frac{2}{\sqrt5} \end {bmatrix} \\ \therefore U=(u_1,u_2)=\begin{bmatrix} \frac{2}{\sqrt5} & -\frac{1}{\sqrt5} \\ \\ \frac{1}{\sqrt5} &\frac{2}{\sqrt5} \end{bmatrix} ui=σi1Avi∴u1=σ11Av1=41 2032 5152 = 5251 ∴u2=σ21Av2=11 2032 −5251 = −5152 ∴U=(u1,u2)= 5251−5152 - 写出表达式
A = U Σ V T = [ 2 5 − 1 5 1 5 2 5 ] [ 4 0 0 1 ] [ 1 5 2 5 − 2 5 1 5 ] A=U\Sigma V^T=\begin{bmatrix} \frac{2}{\sqrt5} & -\frac{1}{\sqrt5} \\ \\ \frac{1}{\sqrt5} &\frac{2}{\sqrt5} \end{bmatrix} \begin{bmatrix} 4 & 0 \\\\ \ 0 & 1\end{bmatrix} \begin{bmatrix} \frac{1}{\sqrt5}& \frac{2}{\sqrt5}\\\\ -\frac{2}{\sqrt5}&\frac{1}{\sqrt5}\end{bmatrix} A=UΣVT= 5251−5152 4 001 51−525251
利用奇异值分解(SVD)进行图片压缩
首先我们先找一张图片来进行实验。

通道分离
对于JPG格式的彩色图片,拥有3个颜色通道,R(红)、G(绿)、B(蓝),那么可以尝试将每个颜色通道进行分离,产生3个形状均为图像高 x 宽 的单通道剧展,即imageR,imageG,imageB。
进行通道分离,将imageArray数组中的每个通道分别单独取出来,得到3个高 × \times × 宽的二维数组。这3个二维数组中每个位置上的取值就是对应像素的某个颜色通道的取值,代码如下:
import numpy as np
from PIL import ImageoriginalImage = Image.open(r'teriri.jpg', 'r')
imageArray = np.array(originalImage)
R = imageArray[:, :, 0]
G = imageArray[:, :, 1]
B = imageArray[:, :, 2]
print(R)
print(G)
print(B)
运行结果如下:
[[207 207 207 … 141 141 141]
[207 207 207 … 141 141 141]
[207 207 207 … 141 141 141]
…
[246 247 248 … 239 239 239]
[246 247 248 … 239 239 239]
[246 247 248 … 239 239 239]]
[[198 198 198 … 126 126 126]
[198 198 198 … 126 126 126]
[198 198 198 … 126 126 126]
…
[233 234 235 … 235 235 235]
[233 234 235 … 235 235 235]
[233 234 235 … 235 235 235]]
[[215 215 215 … 149 147 147]
[215 215 215 … 149 147 147]
[215 215 215 … 149 147 147]
…
[230 231 233 … 203 203 203]
[230 231 233 … 203 203 203]
[230 231 233 … 203 203 203]]
至此,我们成功得到了3个二维ndarray数组,将R、G、B三个通道成功进行了分离。
矩阵压缩
对每个单通道矩阵进行奇异值分解,按照压缩的实际需要取前k个奇异值,进行3个单通道的矩阵的压缩,最后分别形成3个压缩后的矩阵:imageRC,imageGC,imageBC,代码如下:
def imgCompress(channel,percent):U,sigma,V_T = np.linalg.svd(channel)m = U.shape[0]n = V_T.shape[0]reChannel = np.zeros((m,n))for k in range (len(sigma)):reChannel = reChannel + sigma[k] * np.dot(U[:,k].reshape(m,1),V_T[k,:].reshape(1,n))if float(k) / len(sigma) > percent:reChannel[reChannel < 0] = 0reChannel[reChannel > 255] = 255breakreturn np.rint(reChannel).astype("unit8")
图像重建
将经过奇异值分解处理的3个单通道矩阵合并,从而重构出压缩后的彩色图像。
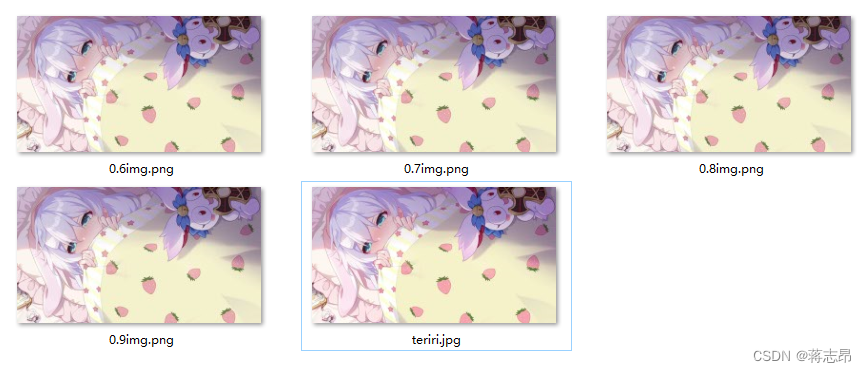
for p in [0.001, 0.005, 0.01, 0.02, 0.03, 0.04, 0.05, 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9]:#p表示取所有奇异值的前多少比例reR = imgCompress(R,p)reG = imgCompress(G,p)reB = imgCompress(B,p)reI = np.stack((reR,reG,reB),2)Image.fromarray(reI).save("{}".format(p)+"img.png")
整体运行结果如下:
比例为0.001至0.04
>0.05至0.5
0.6至原图
总结:
- 取前0.1%奇异值重建的图像是一个非常模糊的,基本只能看到大体轮廓。
- 取前1%奇异值重建的图像就可以看到一个比较清晰的图片了。
- 随着比例的提升,图片越来越清晰,到30%的时候就基本与原图一致了。
相关文章:
奇异值分解在图形压缩中的应用
奇异值分解在图形压缩中的应用 在研究奇异值分解的工程应用之前,我们得明白什么是奇异值?什么是奇异向量? 奇异值与奇异向量 概念:奇异值描述了矩阵在一组特定向量上的行为,奇异向量描述了其最大的作用方向。 奇异值…...

C++深入学习之STL:1、容器部分
标准模板库STL的组成 主要由六大基本组件组成:容器、迭代器、算法、适配器、函数对象(仿函数)以及空间配置器。 容器:就是用来存数据的,也称为数据结构。 本文要详述的是容器主要如下: 序列式容器:vector、list 关联…...

Javascript——vue下载blob文档流
<el-table-column label"操作" fixed"right" width"150" showOverflowTooltip><template slot-scope"scope"><el-button type"text" v-has"stbsd-gjcx-down" class"edit-button" click&…...

C# 的SequenceEqual
SequenceEqual 是 LINQ 扩展方法之一,用于比较两个序列(如数组、列表等)的元素是否相等。 该方法的详细定义如下: public static bool SequenceEqual<TSource>(this IEnumerable<TSource> first, IEnumerable<TS…...
)
第九部分 使用函数 (一)
目录 一、简介 二、函数的调用语法 一、简介 在 Makefile 中可以使用函数来处理变量,从而让我们的命令或是规则更为的灵活和具 有智能。make 所支持的函数也不算很多,不过已经足够我们的操作了。函数调用后,函数 的返回值可以当做变量来使用…...
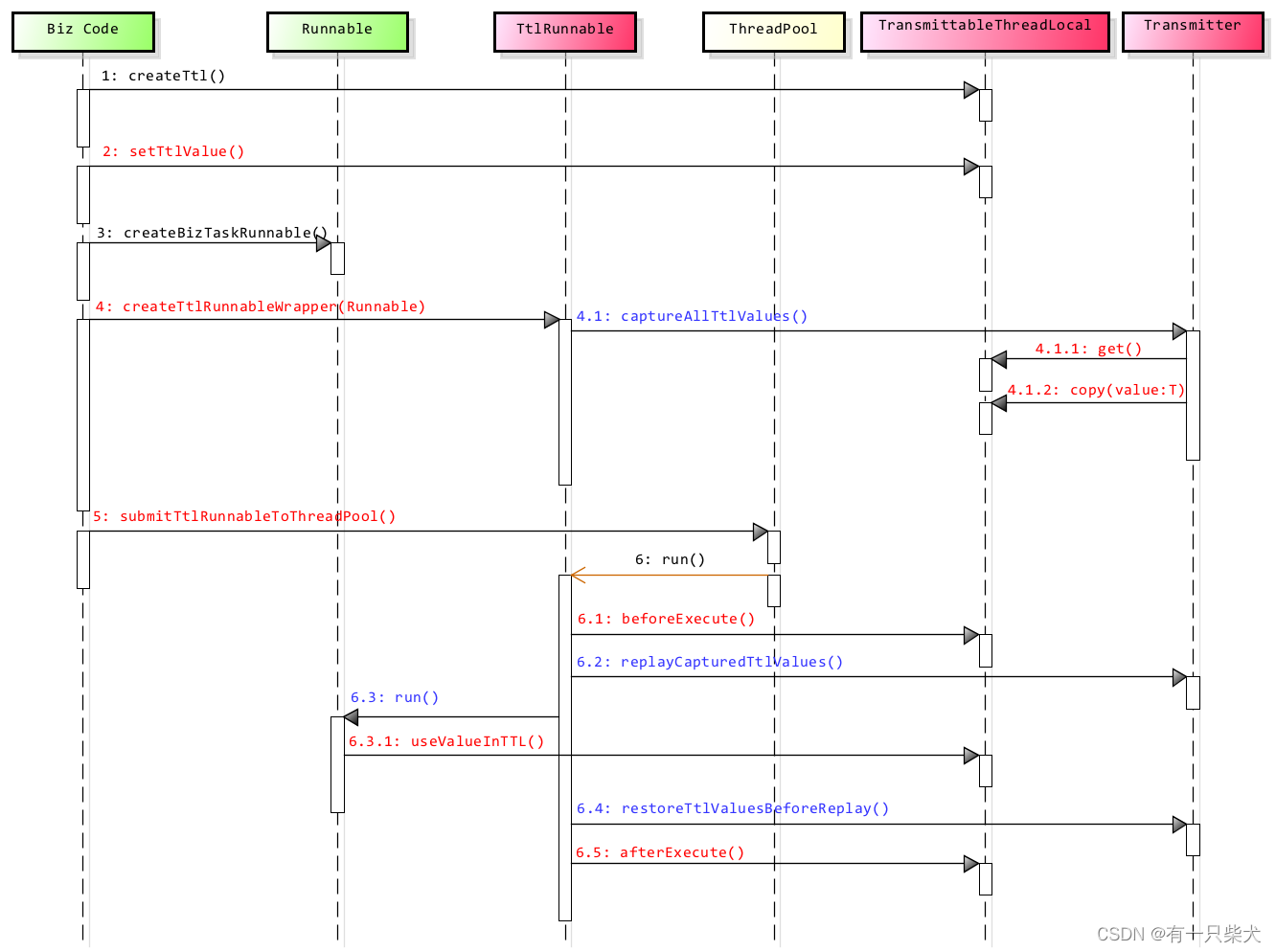
【JUC进阶】14. TransmittableThreadLocal
目录 1、前言 2、TransmittableThreadLocal 2.1、使用场景 2.2、基本使用 3、实现原理 4、小结 1、前言 书接上回《【JUC进阶】13. InheritableThreadLocal》,提到了InheritableThreadLocal虽然能进行父子线程的值传递,但是如果在线程池中&#x…...

基于C++的ORM框架sqlpp11入门介绍(附MySQL运行实例)
基本介绍 sqlpp11 是 C 的类型安全的 SQL 模版库。 Sqlpp11的官方下载地址是, GitHub - rbock/sqlpp11: A type safe SQL template library for C 在这里,可以找到官方的详细介绍文档, https://github.com/rbock/sqlpp11/tree/main/docs…...

对写文章的想法
一些思考 思考初心现在错觉想说的话 最后 思考 在CSDN里面写文章已经快半年了啊,虽然更得不多,但每一篇都花费很多时间,写的时候能帮自己查漏补缺,这边找找资料补充一下,都能去拓展自己的知识面,让自己的文…...
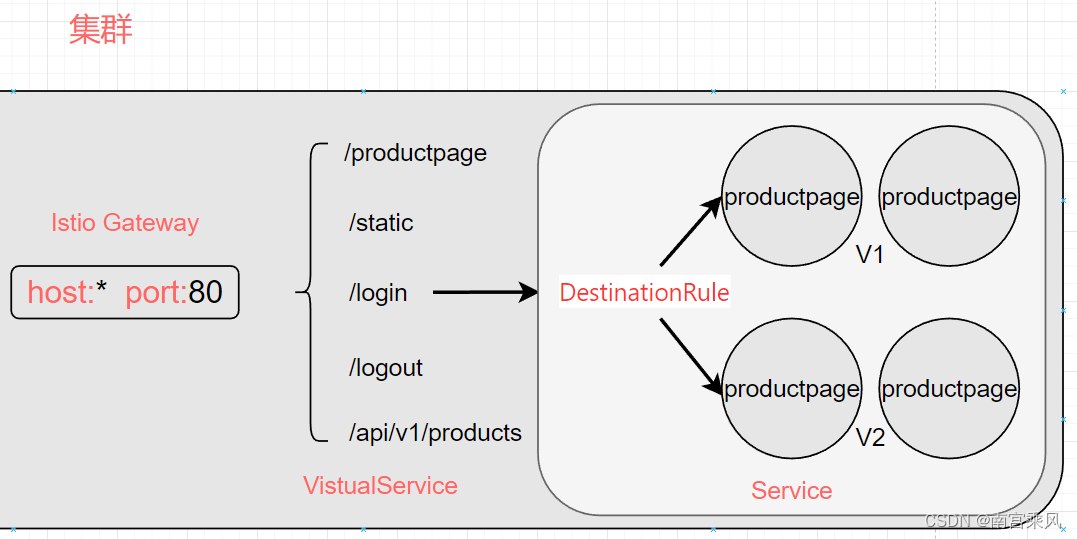
Istio安装和基础原理
1、Istio简介 Istio 是一个开源服务网格,它透明地分层到现有的分布式应用程序上。 Istio 强大的特性提供了一种统一和更有效的方式来保护、连接和监视服务。 Istio 是实现负载平衡、服务到服务身份验证和监视的路径——只需要很少或不需要更改服务代码。它强大的控…...

C++核心编程——基于多态的企业职工系统
本专栏记录C学习过程包括C基础以及数据结构和算法,其中第一部分计划时间一个月,主要跟着黑马视频教程,学习路线如下,不定时更新,欢迎关注。 当前章节处于: ---------第1阶段-C基础入门 ---------第2阶段实战…...
Nginx服务安装
Nginx(发音为[engine x])专为性能优化而开发,其最知名的优点是它的稳定性和低系统资源消 耗,以及对HTTP并发连接的高处理能力(单台物理服务器可支持30000~50000个并发请求)。正因 为如此,大量提供社交网络、…...

微信小程序canvas画布实现矩形元素自由缩放、移动功能
一、获取画布信息并绘制背景 .whml <canvas class="canvas" type="2d" id="myCanvas" bindtouchstart="get_rect_touch_position" bindtouchmove="move_or_scale" bind:tap="finish_edit_check"/> 定义c…...

一文搞懂 Python 3 中的数据类型
介绍 在 Python 中,与所有编程语言一样,数据类型用于对一种特定类型的数据进行分类。这很重要,因为您使用的特定数据类型将决定您可以为其分配哪些值以及您可以对其执行哪些操作(包括可以对其执行哪些操作)。 1. 数字…...
学习笔记之——3D Gaussian Splatting源码解读
之前博客对3DGS进行了学习与调研 学习笔记之——3D Gaussian Splatting及其在SLAM与自动驾驶上的应用调研-CSDN博客文章浏览阅读450次。论文主页3D Gaussian Splatting是最近NeRF方面的突破性工作,它的特点在于重建质量高的情况下还能接入传统光栅化,优…...
Flink standalone集群部署配置
文章目录 简介软件依赖部署方案二、安装1.下载并解压2.ssh免密登录3.修改配置文件3.启动集群4.访问 Web UI 简介 Flink独立模式(Standalone)是部署 Flink 最基本也是最简单的方式:所需要的所有 Flink 组件, 都只是操作系统上运行…...
 方法和 extend()方法的区别和用法)
Python: + 运算符、append() 方法和 extend()方法的区别和用法
在Python中,有几种常见的方式可以向列表中添加元素,其中包括使用 运算符、append() 方法和 extend() 方法。 使用 运算符: 运算符用于合并两个列表。 通过创建一个新列表,包含两个被合并的列表的元素。不会修改原始列表&…...
【MySQL】mysql集群
文章目录 一、mysql日志错误日志查询日志二进制日志慢查询日志redo log和undo log 二、mysql集群主从复制原理介绍配置命令 读写分离原理介绍配置命令 三、mysql分库分表垂直拆分水平拆分 一、mysql日志 MySQL日志 是记录 MySQL 数据库系统运行过程中不同事件和操作的信息的文件…...
zabbix监控windows主机
下载安装zabbix agent安装包 Zabbix官网下载地址: https://www.zabbix.com/cn/download_agents?version5.0LTS&release5.0.40&osWindows&os_versionAny&hardwareamd64&encryptionOpenSSL&packagingMSI&show_legacy0 这里使用zabbix agent2 安装 …...

单例模式的八种写法、单例和并发的关系
文章目录 1.单例模式的作用2.单例模式的适用场景3.饿汉式静态常量(可用)静态代码块(可用) 4.懒汉式线程不安全(不可用)同步方法(线程安全,但不推荐用)同步代码块…...

基于实时Linux+FPGA实现NI CompactRIO系统详解
利用集成的软件工具链,结合信号调理I/O模块,轻松构建和部署实时应用程序。 什么是CompactRIO? CompactRIO系统提供了高处理性能、传感器专用I/O和紧密集成的软件工具,使其成为工业物联网、监测和控制应用的理想之选。实时处理器提…...
详解)
后进先出(LIFO)详解
LIFO 是 Last In, First Out 的缩写,中文译为后进先出。这是一种数据结构的工作原则,类似于一摞盘子或一叠书本: 最后放进去的元素最先出来 -想象往筒状容器里放盘子: (1)你放进的最后一个盘子(…...

C++_核心编程_多态案例二-制作饮品
#include <iostream> #include <string> using namespace std;/*制作饮品的大致流程为:煮水 - 冲泡 - 倒入杯中 - 加入辅料 利用多态技术实现本案例,提供抽象制作饮品基类,提供子类制作咖啡和茶叶*//*基类*/ class AbstractDr…...

java_网络服务相关_gateway_nacos_feign区别联系
1. spring-cloud-starter-gateway 作用:作为微服务架构的网关,统一入口,处理所有外部请求。 核心能力: 路由转发(基于路径、服务名等)过滤器(鉴权、限流、日志、Header 处理)支持负…...
)
进程地址空间(比特课总结)
一、进程地址空间 1. 环境变量 1 )⽤户级环境变量与系统级环境变量 全局属性:环境变量具有全局属性,会被⼦进程继承。例如当bash启动⼦进程时,环 境变量会⾃动传递给⼦进程。 本地变量限制:本地变量只在当前进程(ba…...

.Net框架,除了EF还有很多很多......
文章目录 1. 引言2. Dapper2.1 概述与设计原理2.2 核心功能与代码示例基本查询多映射查询存储过程调用 2.3 性能优化原理2.4 适用场景 3. NHibernate3.1 概述与架构设计3.2 映射配置示例Fluent映射XML映射 3.3 查询示例HQL查询Criteria APILINQ提供程序 3.4 高级特性3.5 适用场…...

ElasticSearch搜索引擎之倒排索引及其底层算法
文章目录 一、搜索引擎1、什么是搜索引擎?2、搜索引擎的分类3、常用的搜索引擎4、搜索引擎的特点二、倒排索引1、简介2、为什么倒排索引不用B+树1.创建时间长,文件大。2.其次,树深,IO次数可怕。3.索引可能会失效。4.精准度差。三. 倒排索引四、算法1、Term Index的算法2、 …...

MySQL 8.0 OCP 英文题库解析(十三)
Oracle 为庆祝 MySQL 30 周年,截止到 2025.07.31 之前。所有人均可以免费考取原价245美元的MySQL OCP 认证。 从今天开始,将英文题库免费公布出来,并进行解析,帮助大家在一个月之内轻松通过OCP认证。 本期公布试题111~120 试题1…...

springboot整合VUE之在线教育管理系统简介
可以学习到的技能 学会常用技术栈的使用 独立开发项目 学会前端的开发流程 学会后端的开发流程 学会数据库的设计 学会前后端接口调用方式 学会多模块之间的关联 学会数据的处理 适用人群 在校学生,小白用户,想学习知识的 有点基础,想要通过项…...

R 语言科研绘图第 55 期 --- 网络图-聚类
在发表科研论文的过程中,科研绘图是必不可少的,一张好看的图形会是文章很大的加分项。 为了便于使用,本系列文章介绍的所有绘图都已收录到了 sciRplot 项目中,获取方式: R 语言科研绘图模板 --- sciRplothttps://mp.…...

Bean 作用域有哪些?如何答出技术深度?
导语: Spring 面试绕不开 Bean 的作用域问题,这是面试官考察候选人对 Spring 框架理解深度的常见方式。本文将围绕“Spring 中的 Bean 作用域”展开,结合典型面试题及实战场景,帮你厘清重点,打破模板式回答,…...

