leetcode每日一题44
130. 被围绕的区域
图论
dfs/bfs
dfs代码框架
void dfs(参数) {if (终止条件) {存放结果;return;}for (选择:本节点所连接的其他节点) {处理节点;dfs(图,选择的节点); // 递归回溯,撤销处理结果}
}
思路:本题要求找到被x围绕的陆地,所以边界的陆地O肯定不符合条件。那么我们只要从周边找到陆地O然后 通过 dfs或者bfs 将周边靠陆地且相邻的陆地O都变成A,然后再去重新遍历地图的时候,把剩下的O变成X,再把所有的A变成O。
- 确认递归函数,参数
一般情况,深搜需要 二维数组数组结构保存所有路径,需要一维数组保存单一路径,这种保存结果的数组,我们可以定义一个全局变量,避免让我们的函数参数过多。
因为需要上下左右遍历,所以构建一个方向坐标
int dir[4][2] = {-1, 0, 0, -1, 1, 0, 0, 1};
递归函数参数为地图,还有当前坐标x,y
void dfs(vector<vector<char>>& board, int x, int y) - 确认终止条件
终止添加不仅是结束本层递归,同时也是我们收获结果的时候。
另外,其实很多dfs写法,没有写终止条件,其实终止条件写在了, 下面dfs递归的逻辑里了,也就是不符合条件,直接不会向下递归。
这个代码的终止条件就是写在递归逻辑里的。
当前方向超出边界,停止当前方向的遍历
for(int i=0;i<4;i++){nextx=x+dir[i][0];nexty=y+dir[i][1];if(nextx<0||nextx>=board.size()||nexty<0||nexty>=board[0].size())continue;}
- 处理目前搜索节点出发的路径
把当前节点改为A
没必要回溯,得到坐标且坐标没有过界,则判断该节点是否是X或者A,若是,则停止当前方向的遍历
若不是,就继续递归
class Solution {
public:int dir[4][2] = {-1, 0, 0, -1, 1, 0, 0, 1}; void dfs(vector<vector<char>>& board, int x, int y){board[x][y]='A';for(int i=0;i<4;i++){int nextx=x+dir[i][0];int nexty=y+dir[i][1];if(nextx<0||nextx>=board.size()||nexty<0||nexty>=board[0].size())continue;if(board[nextx][nexty]=='X'||board[nextx][nexty]=='A')continue;dfs(board, nextx, nexty);}return;}void solve(vector<vector<char>>& board) {int n=board.size(), m=board[0].size();for(int i=0;i<n;i++){if(board[i][0]=='O')dfs(board,i,0);if(board[i][m-1]=='O')dfs(board,i,m-1);}for(int j=0;j<m;j++){if(board[0][j]=='O')dfs(board,0,j);if(board[n-1][j]=='O')dfs(board,n-1,j);}for(int i=0;i<n;i++)for(int j=0;j<m;j++){if (board[i][j] == 'O') board[i][j] = 'X';if (board[i][j] == 'A') board[i][j] = 'O';}return;}
};131. 分割回文串
回溯
切割问题类似组合问题
for循环表示在哪里切下第1刀
递归表示在第一刀的基础上,下面的几刀在哪切
- 递归函数的返回值以及参数
定义两个全局变量,一个用来存放符合条件单一结果,一个用来存放符合条件结果的集合。
vector<vector<string>> result;
vector<string> path;
函数里有两个参数,字符串s,还有记录本层递归的中从哪里开始切的startIndex
void backtracking (const string& s, int startIndex) - 递归函数终止条件
字符串切完了就终止,把当前路径存到结果里
if(startIndex>=s.length()){result.push_back(path);return;
}
- 单层搜索的逻辑
从startIndex开始,遍历startIndex后面所有的位置。如果startIndex到当前位置的字符串是回文子串,则加入当前路径。否则跳过
然后递归当前位置的下一个位置为下一个递归的startIndex
递归结束,回溯,弹出当前字符串
for(int i=startIndex; i<s.length();i++)
{if(isPalindrome(s, startIndex, i)){string str = s.substr(startIndex, i - startIndex + 1);path.push_back(str);}else continue;backtracking(s, i+1);path.pop_back();
}
然后要写是否是回文子串
双指针,一前一后对比
bool isPalindrome(const string& s, int startIndex, int end)
{for(int i=startIndex, int j=end;i<j; i++,j--){if(s[i]!=s[j])return false;}return true;
}
整体代码
class Solution {
public:bool isPalindrome(const string& s, int startIndex, int end){for(int i=startIndex,j=end;i<j; i++,j--){if(s[i]!=s[j])return false;}return true;}vector<vector<string>> result;vector<string> path;void backtracking (const string& s, int startIndex) {if(startIndex>=s.length()){result.push_back(path);return;}for(int i=startIndex; i<s.length();i++){if(isPalindrome(s, startIndex, i)){string str = s.substr(startIndex, i - startIndex + 1);path.push_back(str);}else continue;backtracking(s, i+1);path.pop_back();}return;}vector<vector<string>> partition(string s) {result.clear();path.clear();backtracking(s, 0);return result;}
};
相关文章:

leetcode每日一题44
130. 被围绕的区域 图论 dfs/bfs dfs代码框架 void dfs(参数) {if (终止条件) {存放结果;return;}for (选择:本节点所连接的其他节点) {处理节点;dfs(图,选择的节点); // 递归回溯,撤销处理结果} }思路:本题要求找到被x围绕的陆…...

idea写sql语句快捷键提醒,mapper注解开发,mybatis
第一步:注入SQL语言 1.显示上下文操作(没有这个选项的话就选中sql然后直接alt回车快捷键)2.注入语言或引用 3.mysql 第二步:配置MySQL数据库连接 1.首先点击侧边的数据库,再点击上面的加号 2.点击数据源ÿ…...

002 Golang-channel-practice
第二题: 创建一个生产器和接收器,再建立一个无缓冲的channel。生产器负责把数据放进管道里,接收器负责把管道里面的数据打印出来。这里我们开5个协程把数据打印出来。 直接上代码! package mainimport ("fmt" )func …...
MFC为对话框资源添加类
VC6新建一个对话框类型的工程; 建立之后资源中默认有2个对话框,一个是主对话框,About这个是默认建立的关于版权信息的; 然后主对话框有对应的.h和.cpp文件;可以在其中进行编程; 默认建立的有一个 关于 对话框; 在资源中新插入一个对话框,IDD_DIALOG1是对话框ID; 新加…...
SpringBoot新手入门完整教程和项目示例
文章目录 SpringBoot新手入门完整教程和项目示例1、SpringBoot简介2、Spring Boot的核心功能?(优点)3、SpringBoot与SpringMVC 的区别?4、构建SpringBoot项目4.1、在官网自动生成下载spring boot项目4.2、手动使用maven创建Spring…...
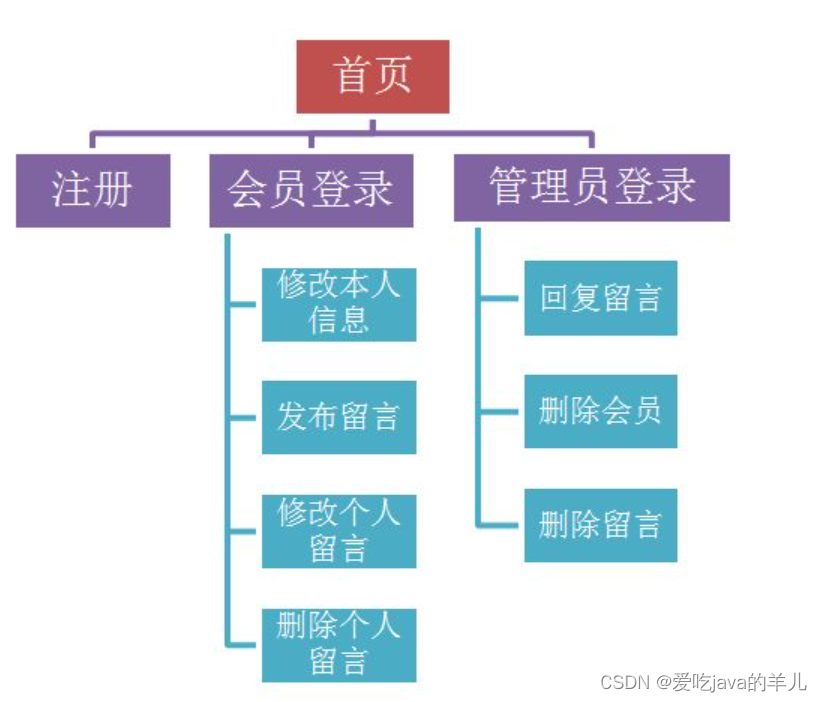
PHP留言板实现
完整教程PHP留言板 登陆界面 一个初学者的留言板(登录和注册)_php留言板登录注册-CSDN博客 留言板功能介绍 百度网盘 请输入提取码 进入百度网盘后,输入提取码:knxt,即可下载项目素材和游客访问页面的模板文件。 &…...
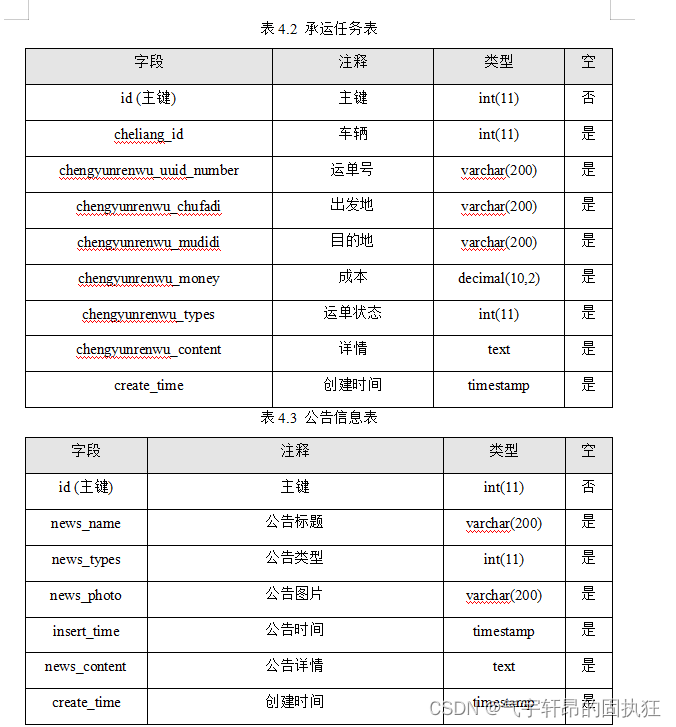
ssm+vue的物流配送人员车辆调度管理系统的设计与实现(有报告)。Javaee项目,ssm vue前后端分离项项目。
演示视频: ssmvue的物流配送人员车辆调度管理系统的设计与实现(有报告)。Javaee项目,ssm vue前后端分离项目。 项目介绍: 采用M(model)V(view)C(controller&…...
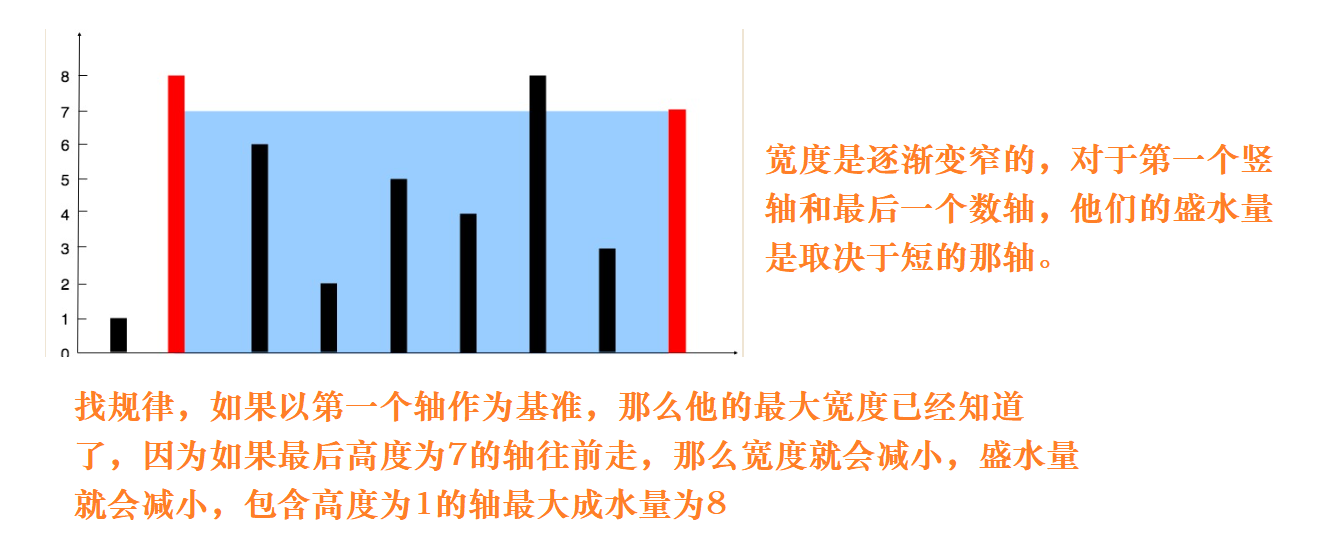
day1·算法-双指针
今天是第一天,GUNDOM带你学算法,跟上我的节奏吗,一起闪击蓝桥杯! 正文展开,今天先上点小菜供大家想用,如有错误或者建议直接放评论区,我会一个一个仔细查看的哦。 双方指针问题一般是在数组中…...

在vue中,切换页面之后如何关闭定时器
在vue中,使用了element-ui的框架,点击左侧切换内部页面。 有些页面使用了定时器,在其换到其他页面的时候,希望能够关闭这些定期请求和复杂操作。 那么,切换页面之后如何关闭定时器?vue的创建流程中没找到能…...
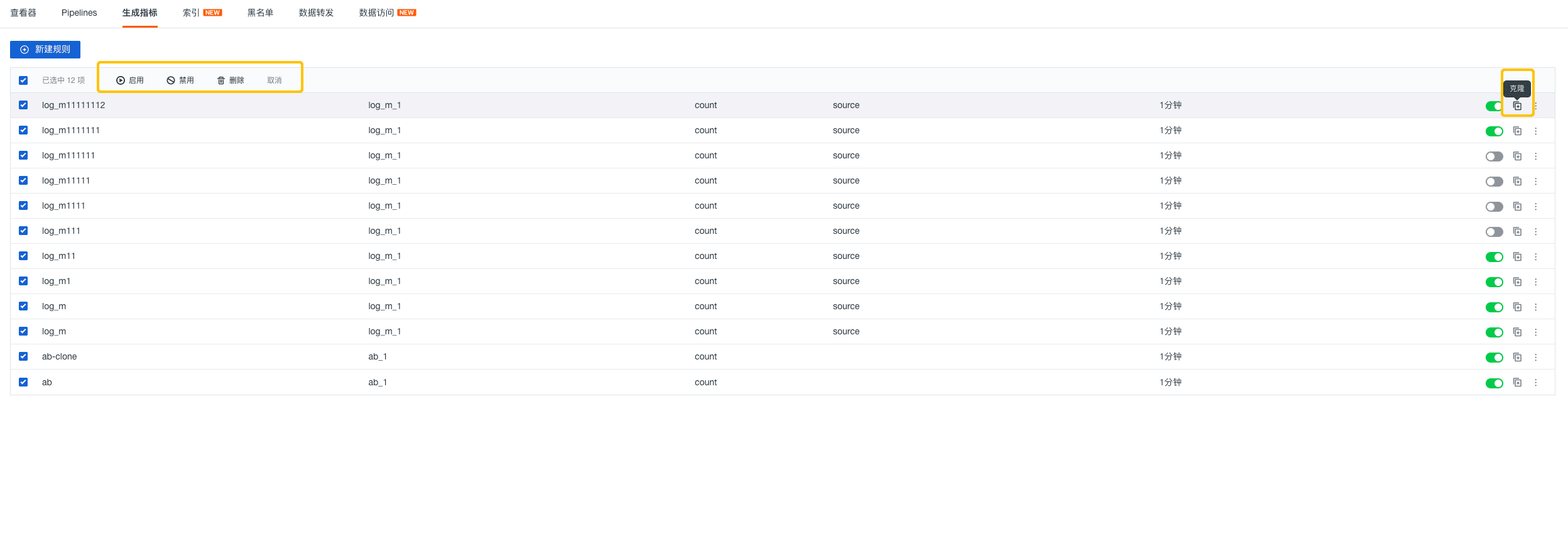
观测云产品更新 | 日志、场景仪表板、监控器等
观测云更新 用户访问监测 (RUM ) 公网 Dataway 支持 ip 转换成地理位置信息。 日志 > 查看器详情页 1、新增 BPF 网络日志采集及日志详情页,支持 Json 格式转化; 2、上述 1 中的日志详情页中新增可读的展示模式,…...
【JupyterLab】在 conda 虚拟环境中 JupyterLab 的安装与使用
【JupyterLab】在 conda 虚拟环境中 JupyterLab 的安装与使用 1 JupyterLab 介绍2 安装2.1 Jupyter Kernel 与 conda 虚拟环境 3 使用3.1 安装中文语言包(Optional)3.2 启动3.3 常用快捷键3.3.1 命令模式下 3.4 远程访问个人计算机3.4.1 局域网下 1 JupyterLab 介绍 官方文档: …...
HTML--JavaScript--引入方式
啊哈~~~基础三剑看到第三剑,JavaScript HTML用于控制网页结构 CSS用于控制网页的外观 JavaScript用于控制网页的行为 JavaScript引入方式 引入的三种方式: 外部JavaScript 内部JavaScript 元素事件JavaScript 引入外部JavaScript 一般情况下网页最好…...
)
第28关 k8s监控实战之Prometheus(七)
大家好,我是博哥爱运维。 今天继续Prometheus的课程,在之前的几节课里面,我带大家认识并部署了prometheus服务,并将一些服务做好了监控,同时通过grafana展示监控数据图表出来。对于怎么使用promql语法,也教…...

SSC | Blue Prism报告:2024年智能自动化(IA)7大趋势预测
近日,RPA行业领导者SS&C | Blue Prism发布《2024智能自动化(IA)趋势与预测》报告。报告中提到,智能自动化(IA)与流程管理的有效融合,是实现数字化转型成功的核心。采用业务流程管理…...
el-tree定义左边箭头,包括下级出现连线
效果图: 代码: <template><div class"agency-wrap"><el-treeclass"filter-tree":data"detailList":props"defaultProps"default-expand-allnode-click"onClickNode":filter-node-me…...

C++ 多线程顺序打印
打印要求: 三个打印线程顺序进行。 线程要求如下: 线程A:打印A 线程B:打印B 线程C:打印C 打印结果: A B C A B C A B C A B C A B C 法一:需要锁和共享变量 #include <iostream>…...

x-cmd pkg | duf - df 命令的现代化替代品
目录 简介用户首次快速实验指南技术特点竞品和相关作品进一步探索 简介 Duf (Disk Usage/Free Utility)是一个磁盘分析工具。其直观的输出和多样化的自定义选项,帮助用户更好地管理和优化存储资源。 用户首次快速实验指南 使用 x duf 即可自…...

202406读书笔记|《沉睡的线条世界》——翻山越岭,只为与你分享点滴的快乐
《沉睡的线条世界》登登登Dn绘著,简简单单的小画,简简单单的线条,简简单单的语言,温馨又有一点暖心。 怎样的你都好,做最真实的自己。 部分节选如下: 愿你我永远有热情,永远能为生活的每一个小惊…...
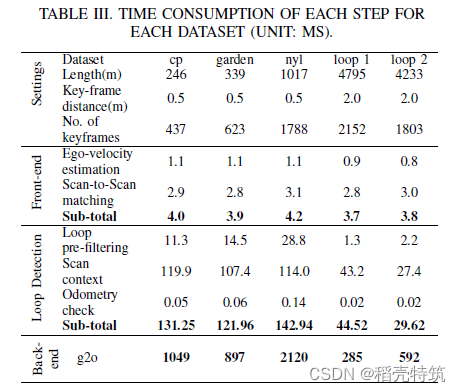
[论文阅读]4DRadarSLAM: A 4D Imaging Radar SLAM System for Large-scale Environments
目录 1.摘要和引言: 2. 系统框架: 2.1 前端: 2.2 回环检测: 2.3 后端: 3.实验和分析: 4.结论 1.摘要和引言: 这篇论文介绍了一种名为“4DRadarSLAM”的新型4D成像雷达SLAM系统࿰…...

Python: vars()详细解释
vars() 是一个内置函数,用于返回一个对象的 __dict__ 属性。它接受一个对象作为参数,如果省略参数,它返回当前局部作用域的字典。 具体而言,vars() 的行为取决于参数的类型: 1. 没有参数: 如果没有提供参…...
: K8s 核心概念白话解读(上):Pod 和 Deployment 究竟是什么?)
云原生核心技术 (7/12): K8s 核心概念白话解读(上):Pod 和 Deployment 究竟是什么?
大家好,欢迎来到《云原生核心技术》系列的第七篇! 在上一篇,我们成功地使用 Minikube 或 kind 在自己的电脑上搭建起了一个迷你但功能完备的 Kubernetes 集群。现在,我们就像一个拥有了一块崭新数字土地的农场主,是时…...

利用ngx_stream_return_module构建简易 TCP/UDP 响应网关
一、模块概述 ngx_stream_return_module 提供了一个极简的指令: return <value>;在收到客户端连接后,立即将 <value> 写回并关闭连接。<value> 支持内嵌文本和内置变量(如 $time_iso8601、$remote_addr 等)&a…...

Redis相关知识总结(缓存雪崩,缓存穿透,缓存击穿,Redis实现分布式锁,如何保持数据库和缓存一致)
文章目录 1.什么是Redis?2.为什么要使用redis作为mysql的缓存?3.什么是缓存雪崩、缓存穿透、缓存击穿?3.1缓存雪崩3.1.1 大量缓存同时过期3.1.2 Redis宕机 3.2 缓存击穿3.3 缓存穿透3.4 总结 4. 数据库和缓存如何保持一致性5. Redis实现分布式…...

大数据零基础学习day1之环境准备和大数据初步理解
学习大数据会使用到多台Linux服务器。 一、环境准备 1、VMware 基于VMware构建Linux虚拟机 是大数据从业者或者IT从业者的必备技能之一也是成本低廉的方案 所以VMware虚拟机方案是必须要学习的。 (1)设置网关 打开VMware虚拟机,点击编辑…...

MMaDA: Multimodal Large Diffusion Language Models
CODE : https://github.com/Gen-Verse/MMaDA Abstract 我们介绍了一种新型的多模态扩散基础模型MMaDA,它被设计用于在文本推理、多模态理解和文本到图像生成等不同领域实现卓越的性能。该方法的特点是三个关键创新:(i) MMaDA采用统一的扩散架构…...

基于Docker Compose部署Java微服务项目
一. 创建根项目 根项目(父项目)主要用于依赖管理 一些需要注意的点: 打包方式需要为 pom<modules>里需要注册子模块不要引入maven的打包插件,否则打包时会出问题 <?xml version"1.0" encoding"UTF-8…...

AI书签管理工具开发全记录(十九):嵌入资源处理
1.前言 📝 在上一篇文章中,我们完成了书签的导入导出功能。本篇文章我们研究如何处理嵌入资源,方便后续将资源打包到一个可执行文件中。 2.embed介绍 🎯 Go 1.16 引入了革命性的 embed 包,彻底改变了静态资源管理的…...

LLMs 系列实操科普(1)
写在前面: 本期内容我们继续 Andrej Karpathy 的《How I use LLMs》讲座内容,原视频时长 ~130 分钟,以实操演示主流的一些 LLMs 的使用,由于涉及到实操,实际上并不适合以文字整理,但还是决定尽量整理一份笔…...

代码规范和架构【立芯理论一】(2025.06.08)
1、代码规范的目标 代码简洁精炼、美观,可持续性好高效率高复用,可移植性好高内聚,低耦合没有冗余规范性,代码有规可循,可以看出自己当时的思考过程特殊排版,特殊语法,特殊指令,必须…...

Canal环境搭建并实现和ES数据同步
作者:田超凡 日期:2025年6月7日 Canal安装,启动端口11111、8082: 安装canal-deployer服务端: https://github.com/alibaba/canal/releases/1.1.7/canal.deployer-1.1.7.tar.gz cd /opt/homebrew/etc mkdir canal…...
