【算法与数据结构】343、LeetCode整数拆分
文章目录
- 一、题目
- 二、解法
- 三、完整代码
所有的LeetCode题解索引,可以看这篇文章——【算法和数据结构】LeetCode题解。
一、题目
二、解法
思路分析:博主做这道题的时候一直在思考,如何找到 k k k个正整数, k k k究竟为多少合适。从数学的逻辑上来说,将 n n n均分为 k k k个数之后, k k k个数的乘积为最大(类似于相同周长下,正方形的面积大于长方形,严格的数学证明不深究了)。本题如果用动态规划的方式,令 d p [ i ] dp[i] dp[i]表示为最大的整数乘积,那么一定可以找到一个 d p [ i − j ] dp[i-j] dp[i−j],使得 d p [ i − j ] ∗ j dp[i-j]*j dp[i−j]∗j最大,并赋值给 d p [ i ] dp[i] dp[i]。而 d p [ i − j ] dp[i-j] dp[i−j]又可以进行类似操作,那么可以一直追溯到 d p [ 0 ] , d p [ 1 ] , d p [ 2 ] dp[0],dp[1],dp[2] dp[0],dp[1],dp[2]。当然,本题当中 d p [ 0 ] , d p [ 1 ] dp[0],dp[1] dp[0],dp[1]没有意义, d p [ 2 ] = 1 dp[2]=1 dp[2]=1。除了 d p [ i − j ] ∗ j dp[i-j]*j dp[i−j]∗j可以得到 d p [ i ] dp[i] dp[i]以外, ( i − j ) ∗ j (i-j)*j (i−j)∗j也可以得到 d p [ i ] dp[i] dp[i],然后我们在每次递归的过程中比较上次的 d p [ i ] dp[i] dp[i]找到最大值。因此, d p [ i ] = m a x ( d p [ i ] , m a x ( d p [ i − j ] ∗ j , ( i − j ) ∗ j ) ) dp[i]=max(dp[i], max(dp[i-j]*j, (i-j)*j)) dp[i]=max(dp[i],max(dp[i−j]∗j,(i−j)∗j))。同时,因为0和1没有意义, i i i从3开始循环,到 n n n。 j j j只要循环到 i / 2 i/2 i/2即可。
程序如下:
class Solution {
public:int integerBreak(int n) {vector<int> dp(n + 1);dp[2] = 1;for (int i = 3; i <= n; i++) {for (int j = 1; j <= i / 2; j++) {dp[i] = max(dp[i], max((i - j) * j, dp[i - j] * j));}}return dp[n];}
};
复杂度分析:
- 时间复杂度: O ( n 2 ) O(n^2) O(n2)。
- 空间复杂度: O ( n ) O(n) O(n)。
三、完整代码
# include <iostream>
# include <vector>
using namespace std;class Solution {
public:int integerBreak(int n) {vector<int> dp(n + 1);dp[2] = 1;for (int i = 3; i <= n; i++) {for (int j = 1; j <= i / 2; j++) {dp[i] = max(dp[i], max((i - j) * j, dp[i - j] * j));}}return dp[n];}
};int main() {Solution s1;int n = 10;int result = s1.integerBreak(n);cout << result << endl;system("pause");return 0;
}
end
相关文章:

【算法与数据结构】343、LeetCode整数拆分
文章目录 一、题目二、解法三、完整代码 所有的LeetCode题解索引,可以看这篇文章——【算法和数据结构】LeetCode题解。 一、题目 二、解法 思路分析:博主做这道题的时候一直在思考,如何找到 k k k个正整数, k k k究竟为多少合适。…...

中级Python面试问题
文章目录 专栏导读1、xrange 和 range 函数有什么区别?2、什么是字典理解?举个例子3、元组理解吗?如果是,怎么做,如果不是,为什么?4、 列表和元组的区别?5、浅拷贝和深拷贝有什么区别…...
Lede(OpenWrt)安装和双宽带叠加
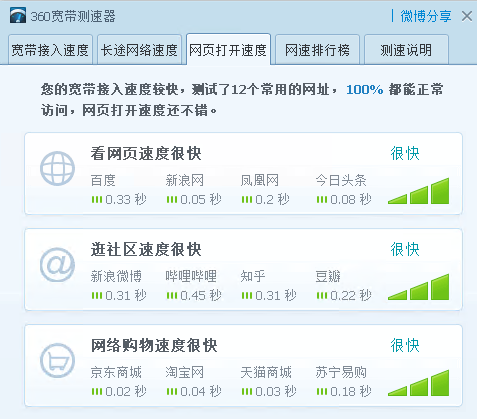
文章目录 一、Lede介绍1. 简介2. 相关网站 二、Lede安装1. 编译环境2. SHELL编译步骤3. 腾讯云自动化助手 三、Lede配置1. 电信接口配置2. 联通接口配置3. 多线多播配置4. 网速测试效果 一、Lede介绍 1. 简介 LEDE是一个专为路由器和嵌入式设备设计的自由和开源的操作系统。 …...

HTML+JS + layer.js +qrcode.min.js 实现二维码弹窗
HTMLJSVUE qrcode.min.js 实现二维码生成 引入qrcode.js创建二维码显示位置编写JS 引入qrcode.js <script type"text/javascript" src"https://static.runoob.com/assets/qrcode/qrcode.min.js"></script>创建二维码显示位置 id 作为 定位标识…...
leetcode 142 环形链表II
题目 给定一个链表的头节点 head ,返回链表开始入环的第一个节点。 如果链表无环,则返回 null。 如果链表中有某个节点,可以通过连续跟踪 next 指针再次到达,则链表中存在环。 为了表示给定链表中的环,评测系统内部使…...

电阻表示方法和电路应用
电阻 电阻的表示方法 直标法 直标法是将电阻器的类别及主要技术参数的数值直接标注在电阻器表面上 通常用3位阿拉伯数字来标注片状电阻的阻值,其中第1位数代表阻值的第1位有效数;第2位数代表阻值的第二位有效数字;第3位数代表阻值倍率&…...
论文笔记(三十九)Learning Human-to-Robot Handovers from Point Clouds
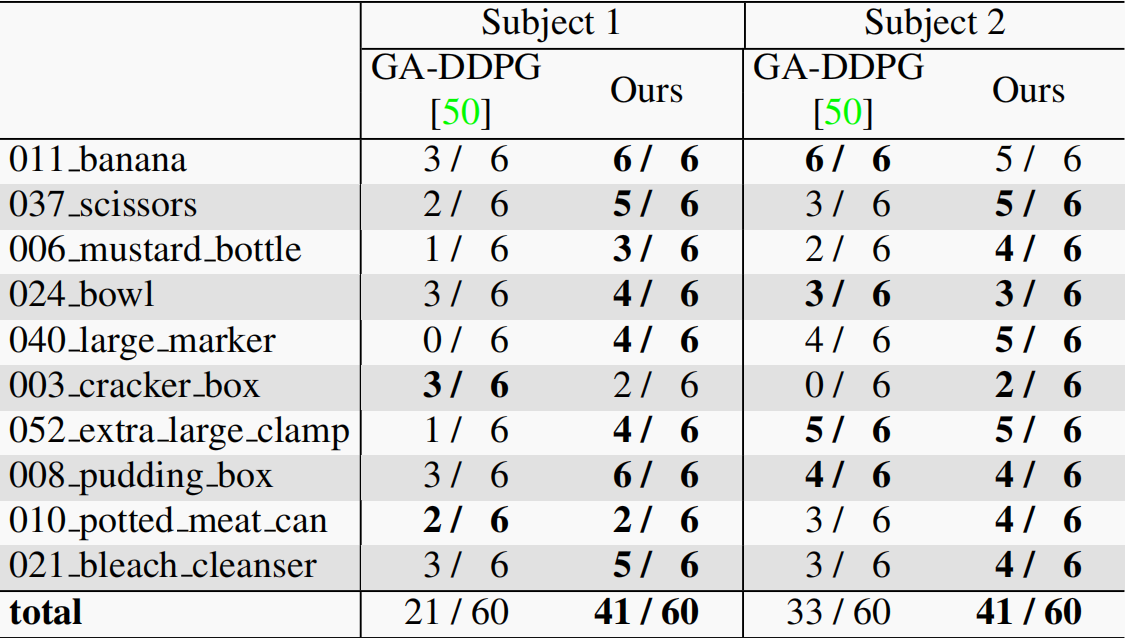
Learning Human-to-Robot Handovers from Point Clouds 文章概括摘要1. 介绍2. 相关工作3. 背景3.1. 强化学习3.2. 移交模拟基准 4. 方法4.1. Handover Environment4.2. 感知4.3. 基于视觉的控制4.4. 师生两阶段培训 (Two-Stage Teacher-Student Training) 5. 实验5.1. 模拟评估…...

浅学Linux之旅 day2 Linux系统及系统安装介绍
答案在时间,耐心是生活的关键 ——24.1.15 一、Linux系统介绍 林纳斯.托瓦兹在1991年开发了Linux内核(开源免费) Linux系统组成 Linux内核 系统库 系统程序 Linux内核和Linux发行版 Linux内核 -> 开源免费,林纳斯开发 Linux发行…...

探索未来餐饮:构建创新连锁餐饮系统的技术之旅
随着数字化时代的发展,连锁餐饮系统的设计和开发不再仅仅关乎订单处理,更是一场充满技术创新的冒险。在本文中,我们将深入研究连锁餐饮系统的技术实现,带你探索未来餐饮业的数字化美食之旅。 1. 构建强大的后端服务 在设计连锁…...
Unity组件开发--AB包打包工具
1.项目工程路径下创建文件夹:ABundles 2.AB包打包脚本: using System.Collections.Generic; using System.IO; using UnityEditor; using UnityEditor.SceneManagement; using UnityEngine; using UnityEngine.SceneManagement;public class AssetBundle…...
毕业设计:基于python微博舆情分析系统+可视化+Django框架 K-means聚类算法(源码)✅
毕业设计:2023-2024年计算机专业毕业设计选题汇总(建议收藏) 毕业设计:2023-2024年最新最全计算机专业毕设选题推荐汇总 🍅感兴趣的可以先收藏起来,点赞、关注不迷路,大家在毕设选题ÿ…...

xbox如何提升下载速度?
提高Xbox的下载速度可以通过以下几种方法: 连接稳定的网络:使用有线以太网连接而不是无线连接,因为有线连接通常更稳定且速度更快。 关闭正在运行的游戏和应用程序:运行游戏或应用程序会消耗网络资源和处理能力,关闭它…...

day13 滑动窗口最大值 前K个高频元素
题目1:239 滑动窗口最大值 题目链接:239 滑动窗口最大值 题意 长度为K的滑动窗口从整数数组的最左侧移动到最右侧,每次只移动1位,求滑动窗口中的最大值 不能使用优先级队列,如果使用大顶堆,最终要pop的…...

Unity——VContainer的依赖注入
一、IOC控制反转和DI依赖倒置 1、IOC框架核心原理是依赖倒置原则 C#设计模式的六大原则 使用这种思想方式,可以让我们无需关心对象的生成方式,只需要告诉容器我需要的对象即可,而告诉容器我需要对象的方式就叫做DI(依赖注入&…...

【面试突击】Spring 面试实战
🌈🌈🌈🌈🌈🌈🌈🌈 欢迎关注公众号(通过文章导读关注:【11来了】),及时收到 AI 前沿项目工具及新技术 的推送 发送 资料 可领取 深入理…...
)
【Linux】Ubuntu 22.04 上安装最新版 Nextcloud Hub 7 (28.0.1)
在 Ubuntu 22.04 上安装 PHP 版本 安装多个 PHP 版本的最简单方法是使用来自 Debian 开发人员 Ondřej Sur 的 PPA。要添加此 PPA,请在终端中运行以下命令。如果要从 PPA 安装软件,则需要 software-properties-common 包。它会自动安装在 Ubuntu 桌面上,但可能会在您的 Ubuntu…...
PHP项目如何自动化测试
开发和测试 测试和开发具有同等重要的作用 从一开始,测试和开发就是相向而行的。测试是开发团队的一支独立的、重要的支柱力量。 测试要具备独立性 独立分析业务需求,独立配置测试环境,独立编写测试脚本,独立开发测试工具。没有…...
WEB 3D技术 three.js 3D贺卡(1) 搭建基本项目环境
好 今天 我也是在网上学的 带着大家一起来做个3D贺卡 首先 我们要创建一个vue3的项目、 先创建一个文件夹 装我们的项目 终端执行 vue create 项目名称 例如 我的名字想叫 greetingCards 就是 vue create greetingcards因为这个名录 里面是全部都小写的 然后 下面选择 vue3 …...

短视频IP运营流程架构SOP模板PPT
【干货资料持续更新,以防走丢】 短视频IP运营流程架构SOP模板PPT 部分资料预览 资料部分是网络整理,仅供学习参考。 抖音运营资料合集(完整资料包含以下内容) 目录 抖音15秒短视频剧本创作公式 在抖音这个短视频平台上&#…...
python爬虫之线程与多进程知识点记录
一、线程 1、概念 线程 在一个进程的内部,要同时干多件事,就需要同时运行多个“子任务”,我们把进程内的这些“子任务”叫做线程 是操作系统能够进行运算调度的最小单位。它被包含在进程之中,是进程中的实际运作单位。一条线程指…...

挑战杯推荐项目
“人工智能”创意赛 - 智能艺术创作助手:借助大模型技术,开发能根据用户输入的主题、风格等要求,生成绘画、音乐、文学作品等多种形式艺术创作灵感或初稿的应用,帮助艺术家和创意爱好者激发创意、提高创作效率。 - 个性化梦境…...

Flask RESTful 示例
目录 1. 环境准备2. 安装依赖3. 修改main.py4. 运行应用5. API使用示例获取所有任务获取单个任务创建新任务更新任务删除任务 中文乱码问题: 下面创建一个简单的Flask RESTful API示例。首先,我们需要创建环境,安装必要的依赖,然后…...
:OpenBCI_GUI:从环境搭建到数据可视化(下))
脑机新手指南(八):OpenBCI_GUI:从环境搭建到数据可视化(下)
一、数据处理与分析实战 (一)实时滤波与参数调整 基础滤波操作 60Hz 工频滤波:勾选界面右侧 “60Hz” 复选框,可有效抑制电网干扰(适用于北美地区,欧洲用户可调整为 50Hz)。 平滑处理&…...

在鸿蒙HarmonyOS 5中实现抖音风格的点赞功能
下面我将详细介绍如何使用HarmonyOS SDK在HarmonyOS 5中实现类似抖音的点赞功能,包括动画效果、数据同步和交互优化。 1. 基础点赞功能实现 1.1 创建数据模型 // VideoModel.ets export class VideoModel {id: string "";title: string ""…...

SCAU期末笔记 - 数据分析与数据挖掘题库解析
这门怎么题库答案不全啊日 来简单学一下子来 一、选择题(可多选) 将原始数据进行集成、变换、维度规约、数值规约是在以下哪个步骤的任务?(C) A. 频繁模式挖掘 B.分类和预测 C.数据预处理 D.数据流挖掘 A. 频繁模式挖掘:专注于发现数据中…...

渗透实战PortSwigger靶场-XSS Lab 14:大多数标签和属性被阻止
<script>标签被拦截 我们需要把全部可用的 tag 和 event 进行暴力破解 XSS cheat sheet: https://portswigger.net/web-security/cross-site-scripting/cheat-sheet 通过爆破发现body可以用 再把全部 events 放进去爆破 这些 event 全部可用 <body onres…...

今日科技热点速览
🔥 今日科技热点速览 🎮 任天堂Switch 2 正式发售 任天堂新一代游戏主机 Switch 2 今日正式上线发售,主打更强图形性能与沉浸式体验,支持多模态交互,受到全球玩家热捧 。 🤖 人工智能持续突破 DeepSeek-R1&…...

Xen Server服务器释放磁盘空间
disk.sh #!/bin/bashcd /run/sr-mount/e54f0646-ae11-0457-b64f-eba4673b824c # 全部虚拟机物理磁盘文件存储 a$(ls -l | awk {print $NF} | cut -d. -f1) # 使用中的虚拟机物理磁盘文件 b$(xe vm-disk-list --multiple | grep uuid | awk {print $NF})printf "%s\n"…...

webpack面试题
面试题:webpack介绍和简单使用 一、webpack(模块化打包工具)1. webpack是把项目当作一个整体,通过给定的一个主文件,webpack将从这个主文件开始找到你项目当中的所有依赖文件,使用loaders来处理它们&#x…...
)
41道Django高频题整理(附答案背诵版)
解释一下 Django 和 Tornado 的关系? Django和Tornado都是Python的web框架,但它们的设计哲学和应用场景有所不同。 Django是一个高级的Python Web框架,鼓励快速开发和干净、实用的设计。它遵循MVC设计,并强调代码复用。Django有…...
