『 C++ 』AVL树详解 ( 万字 )
🦈STL容器类型

在STL的容器中,分为几种容器:
- 序列式容器(Sequence Containers):
- 这些容器以线性顺序存储元素,保留了元素的插入顺序。
- 支持随机访问,因此可以使用索引或迭代器快速访问任何位置的元素。
- 主要的序列式容器包括vector、list、deque、array和forward_list。
- 关联式容器(Associative Containers):
- 这些容器不保留元素的插入顺序,而是根据元素的键进行排序和组织。
- 元素以键值对的形式存储,键通常用于快速查找元素。
- 主要的关联式容器包括set、multiset、map和multimap。
- 无序关联容器(Unordered Associative Containers):
- 这些容器也是键值对容器,但与关联式容器不同,它们不维护元素的排序顺序。
- 使用哈希表(hash table)来组织元素,以便快速查找。
- 主要的无序关联容器包括unordered_set、unordered_multiset、unordered_map和unordered_multimap。
- 容器适配器(Container Adapters):
- 容器适配器是一种特殊类型的容器,它们提供了一种不同于传统容器的接口,通常用于特定的数据结构需求。
- stack是一个适配器,提供了栈(后进先出)的操作。
- queue是一个适配器,提供了队列(先进先出)的操作。
- priority_queue是一个适配器,提供了优先队列的操作,通常用于实现优先级队列。
🦈键值对

键值对,顾名思义其用来表示具有一一对应的关系的一种结构,该结构中一般只包含两个成员变量,即Key与Value;
在STL中存在一种这样的容器template <class T1, class T2> struct pair;;
这个容器是一个类模板,其源码中的底层构造大致为:
template <class T1, class T2>
struct pair {typedef T1 first_type;typedef T2 second_type;T1 first;T2 second;pair() : first(T1()), second(T2()) {}pair(const T1& a, const T2& b) : first(a), second(b) {}
};
可以看到模板参数共有两个分别为T1与T2;
其成员变量只有两个分别为first与second从而能够使该容器具有key与value一对一的关系;
🦈AVL树概念

AVL树(Adelson-Velsky and Landis Tree)它是一种自平衡的二叉搜索树,由苏联的数学家Georgy Adelson-Velsky和Evgenii Landis于1962年首次提出;
AVL树又被称为高度平衡搜索二叉树,它是基于搜索二叉树的基础上的高度平衡搜索二叉树,其性质主要为:
- 它可能是一棵空树(空树可以被看作是一棵AVL树)
- 若该树的左子树不为空,则左子树的所有节点的值都小于根节点的值;若该树的右子树不为空时,该右子树的所有节点都大于根节点的值(搜索二叉树的条件);
- 其左子树与右子树的高度差不超过1;
- AVL树的左右子树也一样为AVL树,意思是每棵’AVL树中的所有子树都应该符合该条件;

以该图为例,该图即为一棵AVL树,其每个节点的左右子树高度差都不超过1;
那么在AVL树的结构中就有几个需要注意的点:
- 如何判断左右子树高度差?
- 如何在插入过程中判断AVL树在插入之后其树的结构是否符合AVL树的规则?
- 当AVL树出现不平衡的状态应该如何调整致使树从不平衡变回AVL树?
🦈AVL树的节点结构

在实现容器或数据结构的过程中可以尽量的使用模板来保证其泛型;对于一棵简单的AVL实现可以根据需要(key模型 或 是key,value模型)来确定实现该数据结构的模板参数个数;
而该篇文章的AVL树实现将针对后者,即key,value模型来进行实现;
AVL树中的节点一般为三叉链结构,即节点内存在三个指针来控制指向,分别为:
_left节点,指向节点的左子树;_right节点,指向节点的右子树;_parent节点,指向节点的父亲节点;
设定义一个变量使用pair<T1,T2>容器来存放插入的数据,其中pair<T1,T2>中的T1对应着key,value模型中的key,T2对应着模型中的value数据;
同时可以设置一个平衡因子变量,以平衡因子的变化来判断该树是否要进行调整,当该树不平衡时则使用某种方式将该树调整回平衡状态,使其结构恢复为AVL树;
template<class K,class V>
struct AVLTreeNode{pair<K, V> _kv;//AVLTreeNode<K, V> *_left;//指向左子树AVLTreeNode<K, V> *_right;//指向右子树AVLTreeNode<K, V> *_parent;//指向其父亲节点int _bf ;//平衡因子AVLTreeNode(const pair<K,V> &kv):_kv(kv),_left(nullptr),_right(nullptr),_parent(nullptr),_bf(0){}
};
🦈AVL树的结构定义

从上文可知,AVL树可以看作是一棵搜索二叉树,其为基于搜索二叉树在此基础上对树做了平衡的操作使其在结构上变得平衡不至于在极端情况下出现"歪脖子树"的情况;
AVL树的定义与平衡搜索二叉树的结构上呈现类似;
template<class K,class V>
class AVLTree{typedef AVLTreeNode<K,V> Node;//将节点进行typedef
public:bool Insert(const K& key);
protected:
private:Node *_root = nullptr;//节点指针
};该篇文章中重点实现AVL树中的插入操作;
🦈AVL树的插入操作

AVL树的插入操作与搜索二叉树的插入操作类似,唯独不同的是AVL树在进行插入操作时需要对树的结构进行判断,即判断插入过后该树是否还符合AVL树的规则(节点的左右子树高度差不超过1);
当树的结构规则被破坏时则需要采用一些特定的方式对树的结构进行调整;
🐡节点插入逻辑

新节点所插入的位置必是为空节点nullprtr,判断所插入数据pair<K,V>中的key值是否大于当前节点;
-
大于当前节点
当所插入数据的
key值大于当前节点数据说明需要插入在该节点的右子树区域; -
小于当前节点
当所插入数据的
key值小于当前节点数据说明需要插入在该节点的左子树区域; -
等于当前节点
当所插入数据的
key值等于当前节点中的数据时,根据搜索二叉树的定义即数据的唯一性,该数据的值已经存在于该树中,该新节点不予插入,返回false;
bool Insert(const std::pair<K,V>& kv){if (_root == nullptr){_root = new Node(kv);return true;}Node *parent = nullptr;Node *cur = _root;//while (cur){/*当cur节点为空时表示该位置可以进行插入*//*插入*/if (cur->_kv.first < kv.first) {parent = cur;cur = cur->_right;}else if (cur->_kv.first > kv.first){parent = cur;cur = cur->_left;}else{//cur->_kv.first == kv.firstreturn false;}}/*与所插入的叶子节点进行链接*/cur = new Node(kv);if (parent->_kv.first < kv.first){parent->_right = cur;}else{parent->_left = cur;}cur->_parent = parent;/*更新平衡因子...判断树的结构规则是否符合AVL树的规则1.符合 不影响下一个节点的插入2.不符合 使用旋转的方式对树进行调整*/return true;}//Insert函数反括号🐡判断树是否符合AVL树的规则

判断树是否符合AVL树的规则有两种:
-
创建子函数
每当插入一个数据时调用子函数来判断树的整体结构是否符合
节点的左右子树高度差不超过1; -
使用平衡因子
使用平衡因子的方式即将AVL树节点的结构中加入一个变量来判断节点的平衡因子;
当平衡因子为
0时表示该节点左右子树高度差为0;当平衡因子为
1或-1时表示该节点的左右子树高度差为1;当平衡因子为
2或-2时表示该节点的左右子树高度差为2,已经不平衡,需要进行特定操作使其恢复AVL树的平衡状态;
在本文中所使用的方式为方式二,即采用平衡因子的方式来对树的节点进行判断;
在上文中提到了对与新节点的插入;
若是搜索二叉树对新节点进行插入时则不需要再对树的结构进行判断,但是在AVL树中则要对AVL树的结构进行判断;
当然再判断树的平衡因子前首先应该在插入节点之后对各个节点的平衡因子进行更新;
对于平衡因子的更新有三种情况:
-
新插入节点的平衡因子
新插入节点的平衡因子必定为0,因为其左右子树都为空节点
nullptr; -
新节点在节点的左子树中
当新节点在节点(新节点的祖先节点)的左子树中时,节点(新节点的祖先节点)的平衡因子需要进行
--; -
新节点在节点的右子树中
当新节点在节点(新节点的祖先节点)的右子树中时,节点(新节点的祖先节点)的平衡因子需要进行
++;
一般平衡因子的更新与平衡因子的检查(树结构的检查)是同一时间的,检查的情况也会出现四种情况:
-
平衡因子更新后为
0当平衡因子在更新过后为
0时则表示这次的插入对树(子树)的平衡状态反而起到了使其平衡的作用;在该次判断后可以直接跳出循环结束插入;
-
平衡因子更新后为
1当平衡因子更新过后为
1时表示这次的插入对树(子树)的平衡状态从完全平衡(左右高度差为0)变成了高度平衡(左右高度差为1),这个变化可能影响到了这个节点的其他的祖先节点,所以应该继续往上进行更新,判断其它的祖先节点是否被影响成非高度平衡状态(左右子树高度差为2); -
平衡因子更新后为
2当平衡因子更新过为
2时表示可以不用再继续向上遍历判断,因为该树(子树)已经不平衡,需要对该树(子树)进行处理;当处理结束之后可直接跳出循环结束插入操作;
-
平衡因子完全错乱
这种情况是避免平衡因子完全错乱;
当上面的三个条件都不满足时则表示平衡因子很可能已经混乱,整棵树的结构获取都变得不平衡,需要直接退出程序并对程序进行检查;
while (parent){if (cur == parent->_left){//新节点为其parent->_bf--;}else // if (cur == parent->_right){parent->_bf++;}/*判断树的结构是否符合AVL树的规则*/if (parent->_bf == 0){// 更新结束break;}else if (parent->_bf == 1 || parent->_bf == -1){/* 继续往上更新可能影响到了该节点的其他祖先节点应继续向上更新并对其祖先节点进行判断其子树是否存在不平衡的状态; */cur = parent;parent = parent->_parent;}else if (parent->_bf == 2 || parent->_bf == -2){/*子树不平衡需要进行旋转操作对树进行调整*/break;}else{/*平衡因子出现问题,对程序断死防止错误插入导致的更大问题*/assert(false);}
🐡旋转操作

AVL树中当其平衡因子的绝对值等于2时表示该节点左右子树的高度差为2,这时候表示这棵AVL树已经不平衡,需要对其进行调整;
那么当AVL树不平衡时如何对树进行操作?
- 采用旋转操作将树的结构进行调整使其变回高度平衡搜索二叉树(AVL树);
对于旋转操作中分为四种操作:
-
左单旋操作
以树(子树)中的某个指定节点作为轴点,对这棵树进行左单旋操作;
-
右单旋操作
以树(子树)中的某个指定节点作为轴点,对这棵树进行右单旋操作;
-
左右双旋操作
以树(子树)中的某个指定节点作为轴点,对这棵树进行左单旋操作;
再以该树(子树)中的另一个指定节点作为轴点,对这棵树进右单旋操作;
-
右左双旋操作
以树(子树)中的某个指定节点作为轴点,对这棵树进行左单旋操作;
再以该树(子树)中的另一个指定节点作为轴点,对这棵树进右单旋操作;
当一棵树(子树)中节点的平衡因子的绝对值为2时将会出现几种情况:
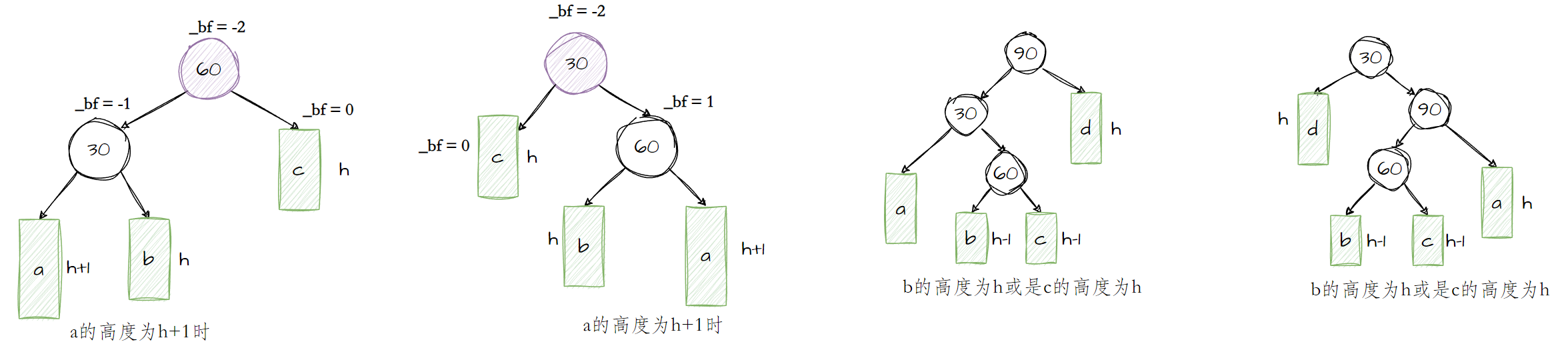
该图分别对应着几种需要进行旋转操作的情况;
那么如何理解几种旋转操作?
- 将以抽象图与实际图结合解释;
🦭右单旋操作

从上文可知,右单旋操作即为以树(子树)中的某个指定节点作为轴点,对这棵树进行右单旋操作;

该图为需要进行右单旋操作树(子树)的抽象图;
当子树a的高度由h变为h+1时由于60节点的左子树高于右子树,其平衡因子由-1变为-2;
a子树的高度变化影响到了其祖先节点;
具象图及变化操作:
-
h为0时
当
h高度为0时,其红色节点即为新增节点,在该处节点新增时将会触发右单旋操作的情况;只需将
cur节点所指向的右子树节点变成parent节点的左子树;parent节点变为cur节点的右子树;在该操作之后在
h高度为0的情况下三个节点的平衡因子都将转化为0,使树的结构恢复为AVL树的结构; -
h为1时
当
h高度为1时,两个红色节点的任意一个节点为新增节点时都将触发右单旋操作的情况;再该中情况中,只需要将
cur节点的右子树curright节点变为parent节点的左子树,再将parent节点变为cur节点的右子树即可;再该操作之后在
h高度为1的情况下parent节点与cur的平衡因子将变为0; -
h为2时相较上面两种场景当中,当
h为2时其的情况将会变得更多;以最单纯的抽象图为例:

当
h为2时,a子树的情况必定为情况①(只有当a子树为情况①时对a处进行新增节点才会触发右单旋操作);b子树与c子树的情况为①②③情况的其中一种;
以该图为例,其旋转操作不再进行赘述;
-
代码片段
void RotateR(Node *parent){ //左高右旋Node *cur = parent->_left;Node *curright = cur->_right;parent->_left = curright;if (curright)curright->_parent = parent;Node *ppnode = parent->_parent;cur->_right = parent;parent->_parent = cur;if (ppnode == nullptr){/*该树若是不为子树其cur节点将更新为根节点*/_root = cur;cur->_parent = nullptr;}else{if (ppnode->_left == parent){ppnode->_left = cur;}else{ppnode->_right = cur;}cur->_parent = ppnode;}parent->_bf = cur->_bf = 0;}
🦭左单旋操作

左单旋与右单旋的操作相反,其几种情况与右单旋的几种情况相同,只不过节点(子树)位置不同;
此处只对左单旋情况中的抽象图进行解析;

该图为例,该图即为需要对左单旋进行操作的情况;
当右子树高度高于左子树且平衡因子等于2时则需要对子树进行旋转操作;
旋转结束之后其cur节点与parent节点的平衡因子将恢复为0;
其结构整体恢复为AVL树的结构状态;
-
代码片段
void RotateL(Node* parent){//右高左旋Node *cur = parent->_right;Node *curleft = cur->_left;parent->_right = curleft;if (curleft){curleft->_parent = parent;}cur->_left = parent;Node *ppnode = parent->_parent;parent->_parent = cur;if (parent == _root){_root = cur;cur->_parent = nullptr;}else{if (ppnode->_left == parent){ppnode->_left = cur;}else{ppnode->_right = cur;}cur->_parent = ppnode;}parent->_bf = cur->_bf = 0;}
🦭左右双旋操作

左右双旋操作,顾名思义在这种情况种需要用到两种单旋的方式使树的结构恢复为以往的AVL树的状态;
-
抽象图

该图即为左右双旋操作的抽象图;
当这种情况时
b子树或者c子树的高度由h转变为h+1时都将破坏该AVL树的结构;当出现这种情况时即需要使用双旋操作来完成对树结构的恢复;
-
为什么当这种情况不能使用单旋操作对树的结构进行恢复?

以该抽象图为例,该抽象图中的
c子树的高度由h-1变为了h;对应的左子树的高度高于右子树,若是用单旋的话需要进行一个右单旋操作;
而再该种情况下若是使用右单旋操作,最终的结果还是一个不平衡的状态;
故在这种情况中不能使用单旋操作来解决AVL树中的不平衡状态;
根据上文所提,在该种情况中只能使用两种单旋操作的方式组合成双旋操作使得最终使得树的结构恢复为平衡状态;

该图即为左右双旋操作的大致操作流程;
从上面的抽象图中也可以衍生几个例子以加深对双旋操作的理解;
-
当树的高度
h为0
当红色节点为新增节点时需要触发左右双旋操作;
-
当树的高度
h为1
当红色节点或绿色节点为新增节点时需要触发左右双旋操作;
该处旋转演示为绿色节点;
-
当树的高度
h为2当树的高度
h为2时,将会有多种情况;
其中
a子树与d子树分别为①②③中的任意一种;下图为树的高度
h为2时的其中一种情况以及旋转方式;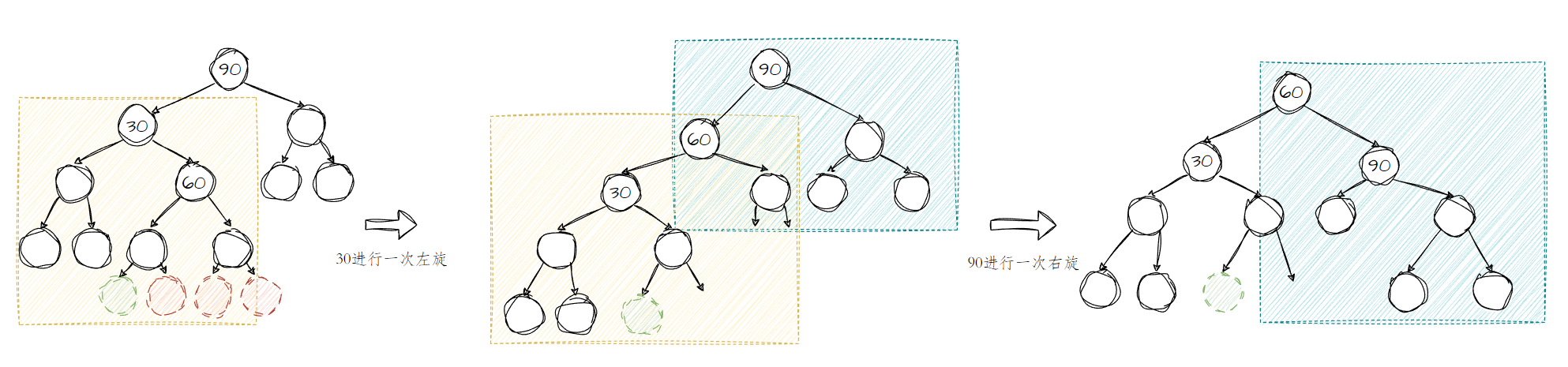
当绿色节点与红色节点其中一个节点为新增节点时需要进行左右双旋操作;
此处旋转操作演示以绿色节点为例;
-
代码段
void RotateLR(Node *parent){Node *cur = parent->_left;Node *curright = cur->_right;int bf = curright->_bf;RotateL(parent->_left);RotateR(parent);/*对平衡因子重新进行调整*/if (bf == 0){parent->_bf = 0;cur->_bf = 0;curright->_bf = 0;}else if (bf == -1){parent->_bf = 1;cur->_bf = 0;curright->_bf = 0;}else if (bf == 1){parent->_bf = 0;cur->_bf = -1;curright->_bf = 0;}}对于双旋操作来说,该操作只需要去调用单旋操作的接口即可;
但除此之外还需要对其中的平衡因子进行调整(在单旋中的平衡因子调整并不是双旋操作所期望的结果,故需要在最后对平衡因子进行调整);
🦭右左双旋操作

右左双旋操作与左右双旋操作相同,只不过调用左单旋接口与右单旋接口的顺序不同,其对应的平衡因子调整也与之不同;

该处直接对几种情况的具象图对右左双旋操作进行解析;
-
具象图情况
-
当树的高度
h为0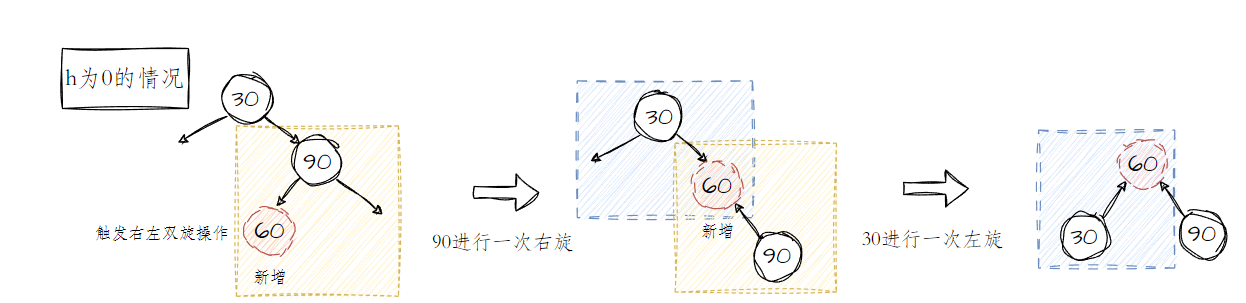
-
当树的高度
h为1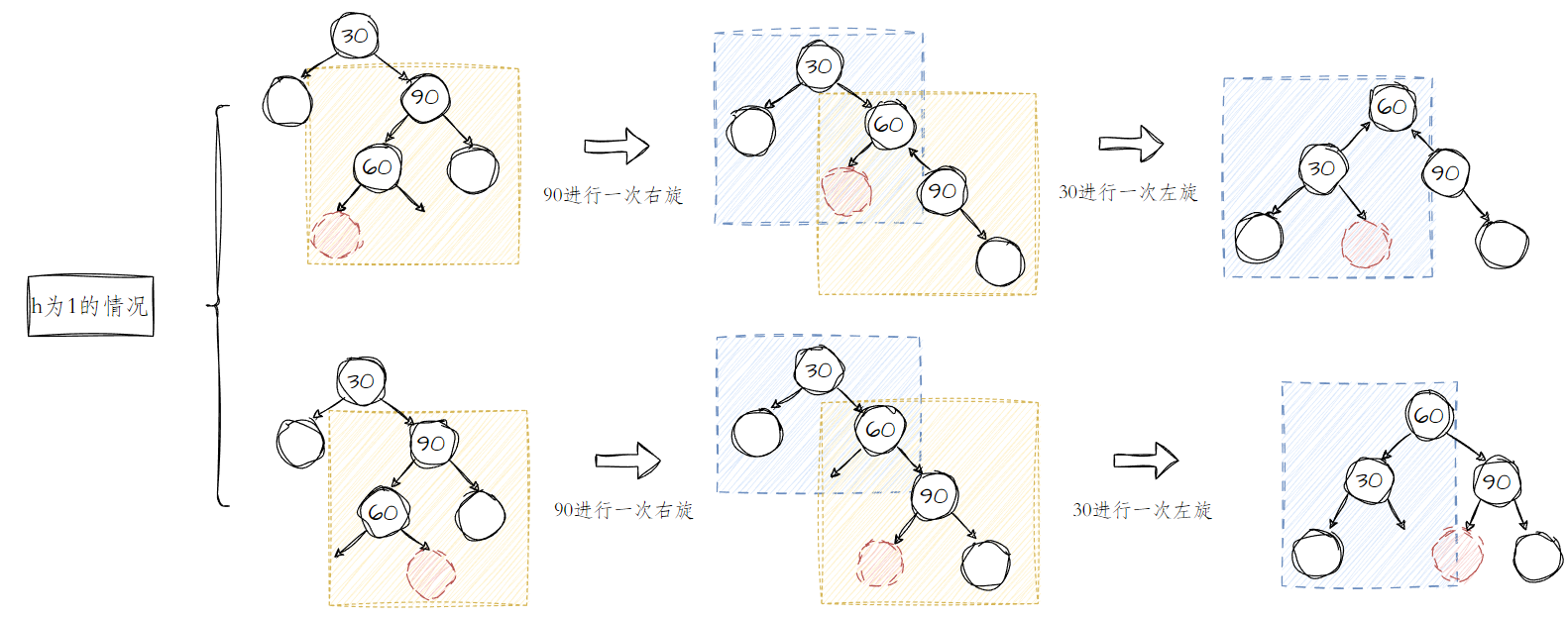
此处演示了其中的两种情况;
-
当树的高度
h为2该处可以类比于左右双旋操作,对此不再进行赘述;
-
-
代码段
void RotateRL(Node *parent){Node *cur = parent->_right;Node *curleft = cur->_left;int bf = curleft->_bf;RotateR(parent->_right);RotateL(parent);/*对平衡因子重新进行调整*/if (bf == 0){cur->_bf = 0;curleft->_bf = 0;parent->_bf = 0;}else if (bf == 1){cur->_bf = 0;curleft->_bf = 0;parent->_bf = -1;}else if (bf == -1){cur->_bf = 1;curleft->_bf = 0;parent->_bf = 0;}else{assert(false);}}
至此插入函数的逻辑到此结束;
🦈检查AVL树是否符合AVL树的规则

- 当插入结束后如何判断所插入的数据以及树的结构是否符合AVL树的性质?
如上题,如何在插入过后对AVL树的结构进行检查,确保在数据插入后能检查此AVL树的实现是否存在问题;
从该问题中可以以上文了解到AVL树的性质规则:
-
左右子树的高度差不超过
1; -
符合搜索二叉树的规则;
左右子树的高度差的判断可以使用两种方法,即采用递归的方式判断该树是否符合AVL树的规则;
由于该树是基于搜索二叉树的规则进行设置,故对于树的存储规则可以不用过分追究;
同时由于树节点的结构中存储了平衡因子,为了防止特殊情况的平衡因子异常导致的树的结构紊乱,应该在检查过程中添加对于平衡因子检查的控制,即一个节点的左右子树的高度差是否符合该节点的平衡因子;
-
代码段
bool IsBalance(){return IsBalance(_root);}bool IsBalance(Node *root){if(root == nullptr){return true;}int leftH = getHeight(root->_left); // the leftH is subtree height for left;int rightH = getHeight(root->_right);if(rightH - leftH != root->_bf){cout << "平衡因子异常:" << root->_kv.first << "->" << root->_bf << endl;return false;}//return abs(rightH - leftH) < 2 && IsBalance(root->_left) && IsBalance(root->_right);}
🦈最终代码

#pragma once#include<iostream>#include<assert.h>using namespace std;template<class K,class V>
struct AVLTreeNode{pair<K, V> _kv;AVLTreeNode<K, V> *_left;AVLTreeNode<K, V> *_right;AVLTreeNode<K, V> *_parent;int _bf ;AVLTreeNode(const pair<K,V> &kv):_kv(kv),_left(nullptr),_right(nullptr),_parent(nullptr),_bf(0){}};template<class K,class V>
class AVLTree{typedef AVLTreeNode<K,V> Node;public:bool Insert(const std::pair<K,V>& kv){if (_root == nullptr){_root = new Node(kv);return true;}Node *parent = nullptr;Node *cur = _root;while (cur){if (cur->_kv.first < kv.first){parent = cur;cur = cur->_right;}else if (cur->_kv.first > kv.first){parent = cur;cur = cur->_left;}else{return false;}}cur = new Node(kv);if (parent->_kv.first < kv.first){parent->_right = cur;}else{parent->_left = cur;}cur->_parent = parent;// ... 控制平衡// 更新平衡因子while (parent){if (cur == parent->_left){parent->_bf--;}else // if (cur == parent->_right){parent->_bf++;}if (parent->_bf == 0){// 更新结束break;}else if (parent->_bf == 1 || parent->_bf == -1){// 继续往上更新cur = parent;parent = parent->_parent;}else if (parent->_bf == 2 || parent->_bf == -2){// 子树不平衡了,需要旋转if (parent->_bf == 2 && cur->_bf == 1){RotateL(parent);}else if (parent->_bf == -2 && cur->_bf == -1){RotateR(parent);}else if (parent->_bf == 2 && cur->_bf == -1){RotateRL(parent);}else if (parent->_bf == -2 && cur->_bf == 1){RotateLR(parent);}break;}else{assert(false);}}return true;}//Insert函数反括号bool IsBalance(){return IsBalance(_root);}bool IsBalance(Node *root){if(root == nullptr){return true;}int leftH = getHeight(root->_left); // the leftH is subtree height for left;int rightH = getHeight(root->_right);if(rightH - leftH != root->_bf){cout << "平衡因子异常:" << root->_kv.first << "->" << root->_bf << endl;return false;}//return abs(rightH - leftH) < 2 && IsBalance(root->_left) && IsBalance(root->_right);}void InOrder(){_InOrder(_root);}protected:int getHeight(){return getHeight(_root);}int getHeight(Node *root){if(root == nullptr){return 0;}int left = getHeight(root->_left);int right = getHeight(root->_right);return left>right?left+1:right+1;}void RotateL(Node* parent){//右高左旋Node *cur = parent->_right;Node *curleft = cur->_left;parent->_right = curleft;if (curleft){curleft->_parent = parent;}cur->_left = parent;Node *ppnode = parent->_parent;parent->_parent = cur;if (parent == _root){_root = cur;cur->_parent = nullptr;}else{if (ppnode->_left == parent){ppnode->_left = cur;}else{ppnode->_right = cur;}cur->_parent = ppnode;}parent->_bf = cur->_bf = 0;}void RotateR(Node *parent){ //左高右旋Node *cur = parent->_left;Node *curright = cur->_right;parent->_left = curright;if (curright)curright->_parent = parent;Node *ppnode = parent->_parent;cur->_right = parent;parent->_parent = cur;if (ppnode == nullptr){_root = cur;cur->_parent = nullptr;}else{if (ppnode->_left == parent){ppnode->_left = cur;}else{ppnode->_right = cur;}cur->_parent = ppnode;}parent->_bf = cur->_bf = 0;}void RotateLR(Node *parent){Node *cur = parent->_left;Node *curright = cur->_right;int bf = curright->_bf;RotateL(parent->_left);RotateR(parent);if (bf == 0){parent->_bf = 0;cur->_bf = 0;curright->_bf = 0;}else if (bf == -1){parent->_bf = 1;cur->_bf = 0;curright->_bf = 0;}else if (bf == 1){parent->_bf = 0;cur->_bf = -1;curright->_bf = 0;}}void RotateRL(Node *parent){Node *cur = parent->_right;Node *curleft = cur->_left;int bf = curleft->_bf;RotateR(parent->_right);RotateL(parent);if (bf == 0){cur->_bf = 0;curleft->_bf = 0;parent->_bf = 0;}else if (bf == 1){cur->_bf = 0;curleft->_bf = 0;parent->_bf = -1;}else if (bf == -1){cur->_bf = 1;curleft->_bf = 0;parent->_bf = 0;}else{assert(false);}}void _InOrder(const Node *root){if (root == nullptr)return;_InOrder(root->_left);std::cout << root->_kv.first << " : " << root->_kv.second << std::endl;_InOrder(root->_right);}private:Node *_root = nullptr;
};相关文章:

『 C++ 』AVL树详解 ( 万字 )
🦈STL容器类型 在STL的容器中,分为几种容器: 序列式容器(Sequence Containers): 这些容器以线性顺序存储元素,保留了元素的插入顺序。 支持随机访问,因此可以使用索引或迭代器快速访问任何位置的元素。 主要的序列式…...

Python下载安装pip方法与步骤_pip国内镜像
前提:下载安装好 python 打开命令提示符winR->cmd(不需要进入 python,直接在终端输入指令执行即可,也可以再 pycharm 终端执行命令)加入要安装ipython,需要执行以下命令: pip install **<…...
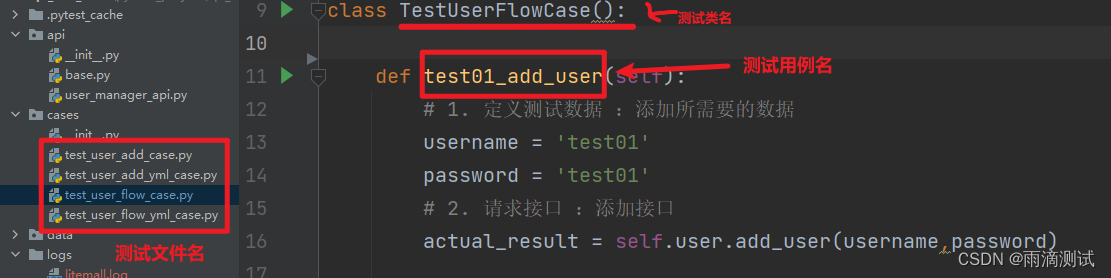
自动化测试框架pytest系列之基础概念介绍(一)
如果你要打算学习自动化测试 ,无论是web自动化、app自动化还是接口自动化 ,在学习的道路上,你几乎会遇到pytest这个测试框架,因为自动化编写没有测试框架,根本玩不了 。 如果你已经是一位自动化测试人员 ,…...

编码技巧:如何在Golang中高效解析和生成XML
编码技巧:如何在Golang中高效解析和生成XML 引言Golang中的XML基础解析XML文件生成XML文件错误处理和调试高级技巧和最佳实践总结 引言 在当今数据驱动的编程世界中,有效地处理各种数据格式是每个开发人员必备的技能之一。其中,XMLÿ…...

24校招,帆书测试开发工程师一面
前言 樊高读书是帆书的前身,我之前还看过他们的书,缘分闭环了 时间:25min 平台:飞书视频面试 过程 自我介绍为啥从后端转测试?通过实习经历,对测试有什么了解?讲一下游戏测试经历负责什么业…...

Java 方法以及在计算机内部的调用问题
修饰符 返回值类型 方法名( 形参列表 ){ 方法体代码(需要执行的功能代码) return 返回值; } 方法在内种没有先后顺序,但是不能把一个方法定义在另一个方法中。 方法的返回值类型写void(无返回申明)时,方法内不能使用return返回数…...
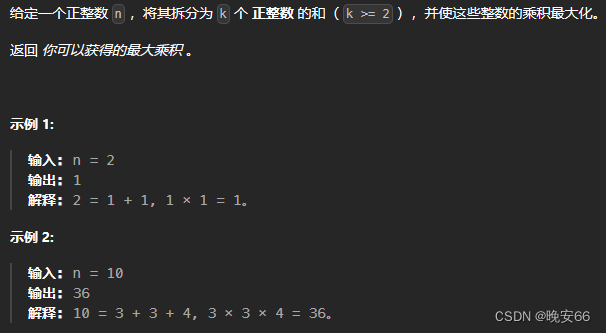
【算法与数据结构】343、LeetCode整数拆分
文章目录 一、题目二、解法三、完整代码 所有的LeetCode题解索引,可以看这篇文章——【算法和数据结构】LeetCode题解。 一、题目 二、解法 思路分析:博主做这道题的时候一直在思考,如何找到 k k k个正整数, k k k究竟为多少合适。…...

中级Python面试问题
文章目录 专栏导读1、xrange 和 range 函数有什么区别?2、什么是字典理解?举个例子3、元组理解吗?如果是,怎么做,如果不是,为什么?4、 列表和元组的区别?5、浅拷贝和深拷贝有什么区别…...
Lede(OpenWrt)安装和双宽带叠加
文章目录 一、Lede介绍1. 简介2. 相关网站 二、Lede安装1. 编译环境2. SHELL编译步骤3. 腾讯云自动化助手 三、Lede配置1. 电信接口配置2. 联通接口配置3. 多线多播配置4. 网速测试效果 一、Lede介绍 1. 简介 LEDE是一个专为路由器和嵌入式设备设计的自由和开源的操作系统。 …...

HTML+JS + layer.js +qrcode.min.js 实现二维码弹窗
HTMLJSVUE qrcode.min.js 实现二维码生成 引入qrcode.js创建二维码显示位置编写JS 引入qrcode.js <script type"text/javascript" src"https://static.runoob.com/assets/qrcode/qrcode.min.js"></script>创建二维码显示位置 id 作为 定位标识…...
leetcode 142 环形链表II
题目 给定一个链表的头节点 head ,返回链表开始入环的第一个节点。 如果链表无环,则返回 null。 如果链表中有某个节点,可以通过连续跟踪 next 指针再次到达,则链表中存在环。 为了表示给定链表中的环,评测系统内部使…...

电阻表示方法和电路应用
电阻 电阻的表示方法 直标法 直标法是将电阻器的类别及主要技术参数的数值直接标注在电阻器表面上 通常用3位阿拉伯数字来标注片状电阻的阻值,其中第1位数代表阻值的第1位有效数;第2位数代表阻值的第二位有效数字;第3位数代表阻值倍率&…...
论文笔记(三十九)Learning Human-to-Robot Handovers from Point Clouds
Learning Human-to-Robot Handovers from Point Clouds 文章概括摘要1. 介绍2. 相关工作3. 背景3.1. 强化学习3.2. 移交模拟基准 4. 方法4.1. Handover Environment4.2. 感知4.3. 基于视觉的控制4.4. 师生两阶段培训 (Two-Stage Teacher-Student Training) 5. 实验5.1. 模拟评估…...

浅学Linux之旅 day2 Linux系统及系统安装介绍
答案在时间,耐心是生活的关键 ——24.1.15 一、Linux系统介绍 林纳斯.托瓦兹在1991年开发了Linux内核(开源免费) Linux系统组成 Linux内核 系统库 系统程序 Linux内核和Linux发行版 Linux内核 -> 开源免费,林纳斯开发 Linux发行…...

探索未来餐饮:构建创新连锁餐饮系统的技术之旅
随着数字化时代的发展,连锁餐饮系统的设计和开发不再仅仅关乎订单处理,更是一场充满技术创新的冒险。在本文中,我们将深入研究连锁餐饮系统的技术实现,带你探索未来餐饮业的数字化美食之旅。 1. 构建强大的后端服务 在设计连锁…...
Unity组件开发--AB包打包工具
1.项目工程路径下创建文件夹:ABundles 2.AB包打包脚本: using System.Collections.Generic; using System.IO; using UnityEditor; using UnityEditor.SceneManagement; using UnityEngine; using UnityEngine.SceneManagement;public class AssetBundle…...
毕业设计:基于python微博舆情分析系统+可视化+Django框架 K-means聚类算法(源码)✅
毕业设计:2023-2024年计算机专业毕业设计选题汇总(建议收藏) 毕业设计:2023-2024年最新最全计算机专业毕设选题推荐汇总 🍅感兴趣的可以先收藏起来,点赞、关注不迷路,大家在毕设选题ÿ…...

xbox如何提升下载速度?
提高Xbox的下载速度可以通过以下几种方法: 连接稳定的网络:使用有线以太网连接而不是无线连接,因为有线连接通常更稳定且速度更快。 关闭正在运行的游戏和应用程序:运行游戏或应用程序会消耗网络资源和处理能力,关闭它…...

day13 滑动窗口最大值 前K个高频元素
题目1:239 滑动窗口最大值 题目链接:239 滑动窗口最大值 题意 长度为K的滑动窗口从整数数组的最左侧移动到最右侧,每次只移动1位,求滑动窗口中的最大值 不能使用优先级队列,如果使用大顶堆,最终要pop的…...

Unity——VContainer的依赖注入
一、IOC控制反转和DI依赖倒置 1、IOC框架核心原理是依赖倒置原则 C#设计模式的六大原则 使用这种思想方式,可以让我们无需关心对象的生成方式,只需要告诉容器我需要的对象即可,而告诉容器我需要对象的方式就叫做DI(依赖注入&…...

CTF show Web 红包题第六弹
提示 1.不是SQL注入 2.需要找关键源码 思路 进入页面发现是一个登录框,很难让人不联想到SQL注入,但提示都说了不是SQL注入,所以就不往这方面想了 先查看一下网页源码,发现一段JavaScript代码,有一个关键类ctfs…...

docker详细操作--未完待续
docker介绍 docker官网: Docker:加速容器应用程序开发 harbor官网:Harbor - Harbor 中文 使用docker加速器: Docker镜像极速下载服务 - 毫秒镜像 是什么 Docker 是一种开源的容器化平台,用于将应用程序及其依赖项(如库、运行时环…...

逻辑回归:给不确定性划界的分类大师
想象你是一名医生。面对患者的检查报告(肿瘤大小、血液指标),你需要做出一个**决定性判断**:恶性还是良性?这种“非黑即白”的抉择,正是**逻辑回归(Logistic Regression)** 的战场&a…...

Java 8 Stream API 入门到实践详解
一、告别 for 循环! 传统痛点: Java 8 之前,集合操作离不开冗长的 for 循环和匿名类。例如,过滤列表中的偶数: List<Integer> list Arrays.asList(1, 2, 3, 4, 5); List<Integer> evens new ArrayList…...

FFmpeg 低延迟同屏方案
引言 在实时互动需求激增的当下,无论是在线教育中的师生同屏演示、远程办公的屏幕共享协作,还是游戏直播的画面实时传输,低延迟同屏已成为保障用户体验的核心指标。FFmpeg 作为一款功能强大的多媒体框架,凭借其灵活的编解码、数据…...

《通信之道——从微积分到 5G》读书总结
第1章 绪 论 1.1 这是一本什么样的书 通信技术,说到底就是数学。 那些最基础、最本质的部分。 1.2 什么是通信 通信 发送方 接收方 承载信息的信号 解调出其中承载的信息 信息在发送方那里被加工成信号(调制) 把信息从信号中抽取出来&am…...

拉力测试cuda pytorch 把 4070显卡拉满
import torch import timedef stress_test_gpu(matrix_size16384, duration300):"""对GPU进行压力测试,通过持续的矩阵乘法来最大化GPU利用率参数:matrix_size: 矩阵维度大小,增大可提高计算复杂度duration: 测试持续时间(秒&…...

Android15默认授权浮窗权限
我们经常有那种需求,客户需要定制的apk集成在ROM中,并且默认授予其【显示在其他应用的上层】权限,也就是我们常说的浮窗权限,那么我们就可以通过以下方法在wms、ams等系统服务的systemReady()方法中调用即可实现预置应用默认授权浮…...

实现弹窗随键盘上移居中
实现弹窗随键盘上移的核心思路 在Android中,可以通过监听键盘的显示和隐藏事件,动态调整弹窗的位置。关键点在于获取键盘高度,并计算剩余屏幕空间以重新定位弹窗。 // 在Activity或Fragment中设置键盘监听 val rootView findViewById<V…...

CMake控制VS2022项目文件分组
我们可以通过 CMake 控制源文件的组织结构,使它们在 VS 解决方案资源管理器中以“组”(Filter)的形式进行分类展示。 🎯 目标 通过 CMake 脚本将 .cpp、.h 等源文件分组显示在 Visual Studio 2022 的解决方案资源管理器中。 ✅ 支持的方法汇总(共4种) 方法描述是否推荐…...
