数据结构——二叉树(先序、中序、后序及层次四种遍历(C语言版))超详细~ (✧∇✧) Q_Q
目录
二叉树的定义:
*特殊的二叉树:
二叉树的性质:
二叉树的声明:
二叉树的先序遍历:
二叉树的中序遍历:
二叉树的后序遍历:
二叉树的层序遍历:
二叉树的节点个数:
二叉树叶节点个数:
最后完整代码:
运行结果:
二叉树的定义:
- 二叉树是n(n≥0)个结点的有限集合:
① 或者为空二叉树,即n = 0。
② 或者由一个根结点和两个互不相交的被称为根的左子树和右子树组成。左子树和右子树又分别是一棵二叉树。 - 特点:①每个结点至多只有两棵子树 ②左右子树不能颠倒(二叉树是有序树)【注意区别:度为2的有序树】
一颗普通的二叉树(栗子):
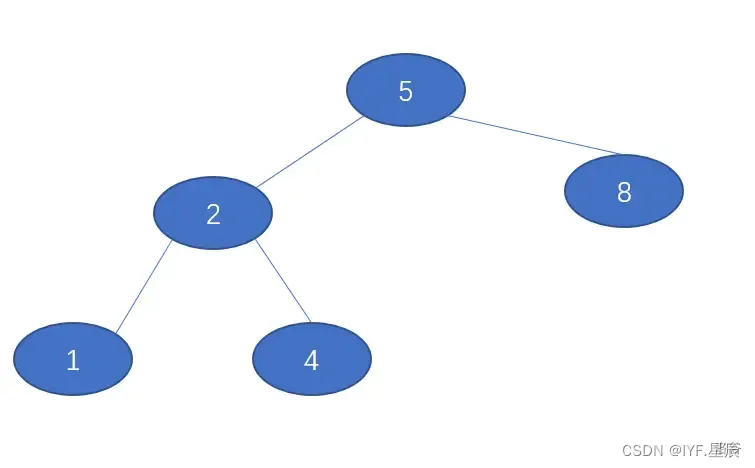
*特殊的二叉树:
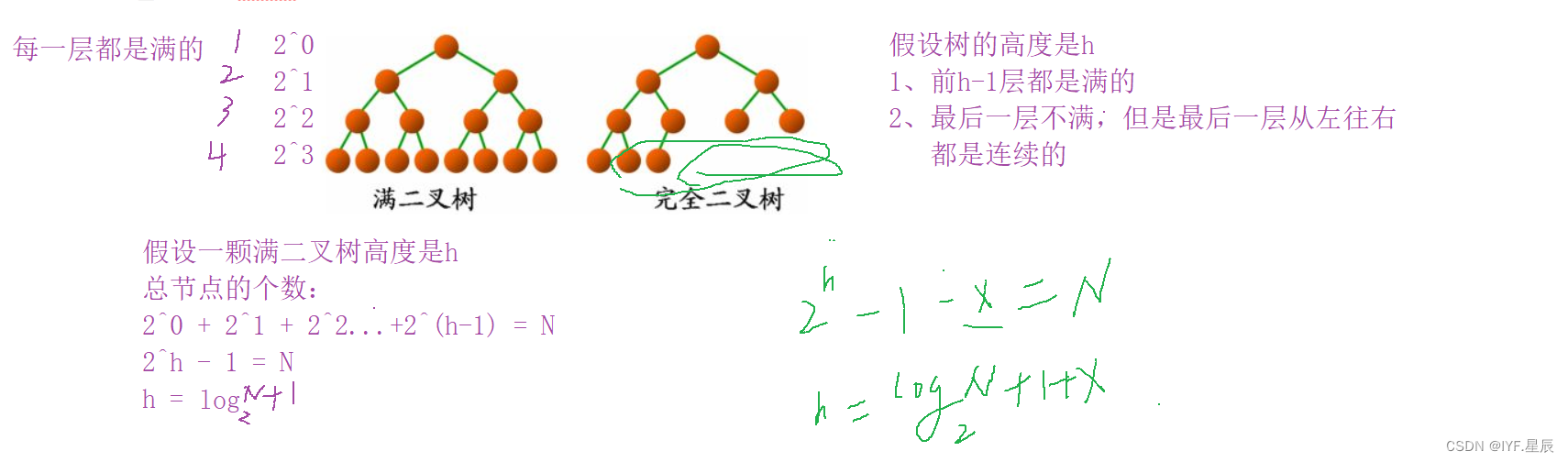
1.满二叉树:一个二叉树,如果每一个层的节点数都达到最大值,则这个二叉树就是满二叉树。也就是说,一个二叉树的层数为k,且节点总数是(2^k-1),则它就是满二叉树。
2.完全二叉树:完全二叉树是效率很高的数据结构,完全二叉树是由满二叉树而引出来的。对于深度为k的,有n个节点的二叉树,当且仅当其每一个节点与k都与其深度为k的满二叉树中编号从1至n的节点一一对应时称之为完全二叉树。注意满二叉树是一种特殊的完全二叉树。
二叉树的性质:
1.若规定根节点的层数为1,则一颗非空二叉树的第i层上最多有2^(i-1)个节点
2.若规定根节点的层数为1,则其深度为h的二叉树的最大节点数是2^h-1
3.对任何一颗二叉树,如果度为0期叶节点个数为n0,度为2的分支节点个数为n2,则有n0=n2+1;
即度为0的叶节点比度为2的分支节点多1
4.若规定根节点的层数为1,具有n个节点的满二叉树的深度h=log2(N+1).

二叉树的声明:
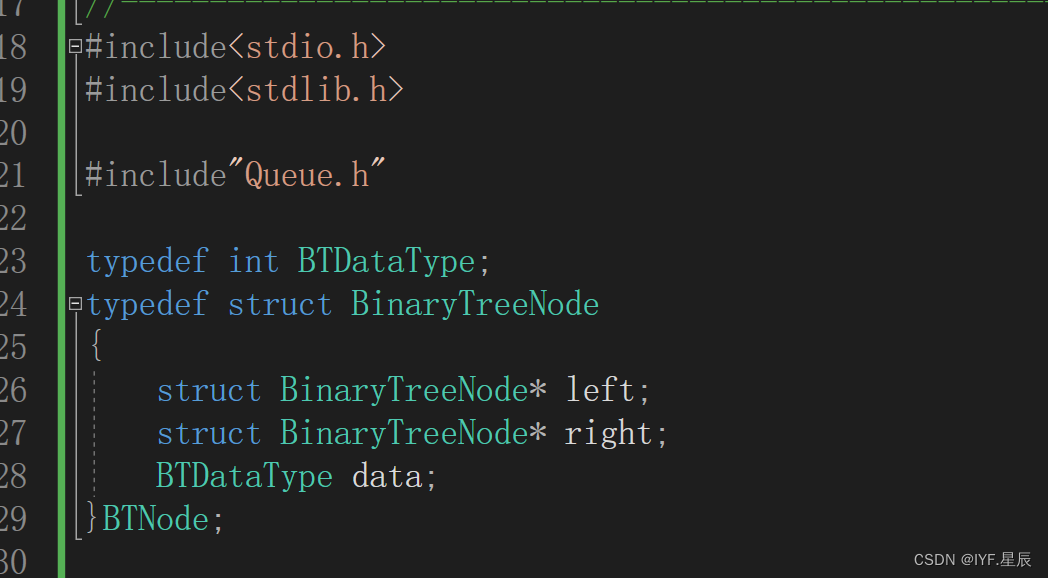
为了方便后续的操作与理解,这里给出二叉树的声明
二叉树的先序遍历:
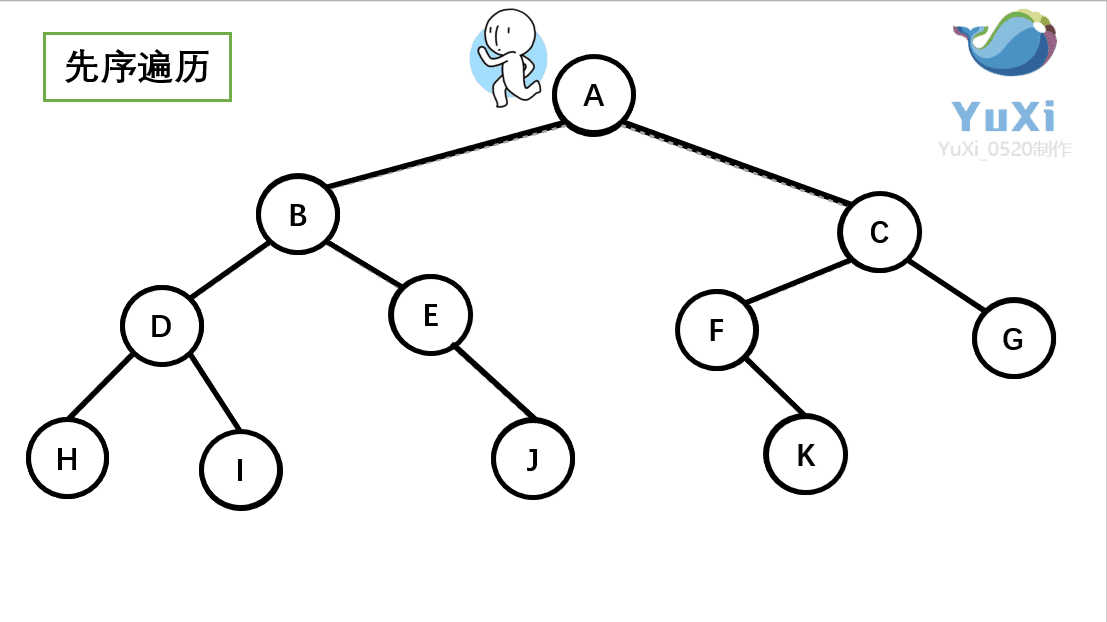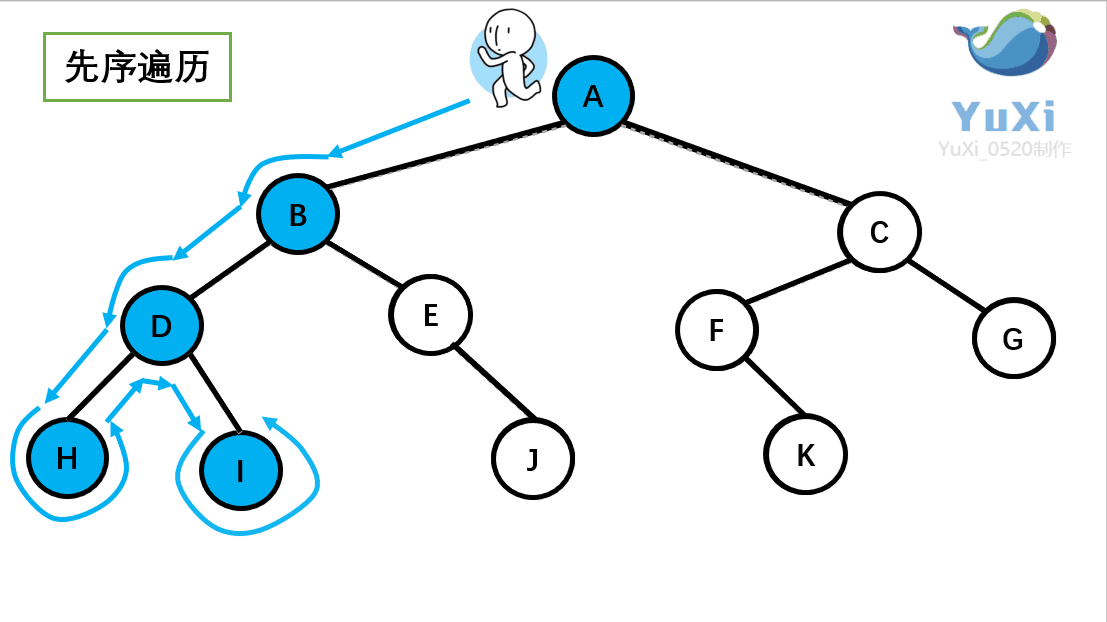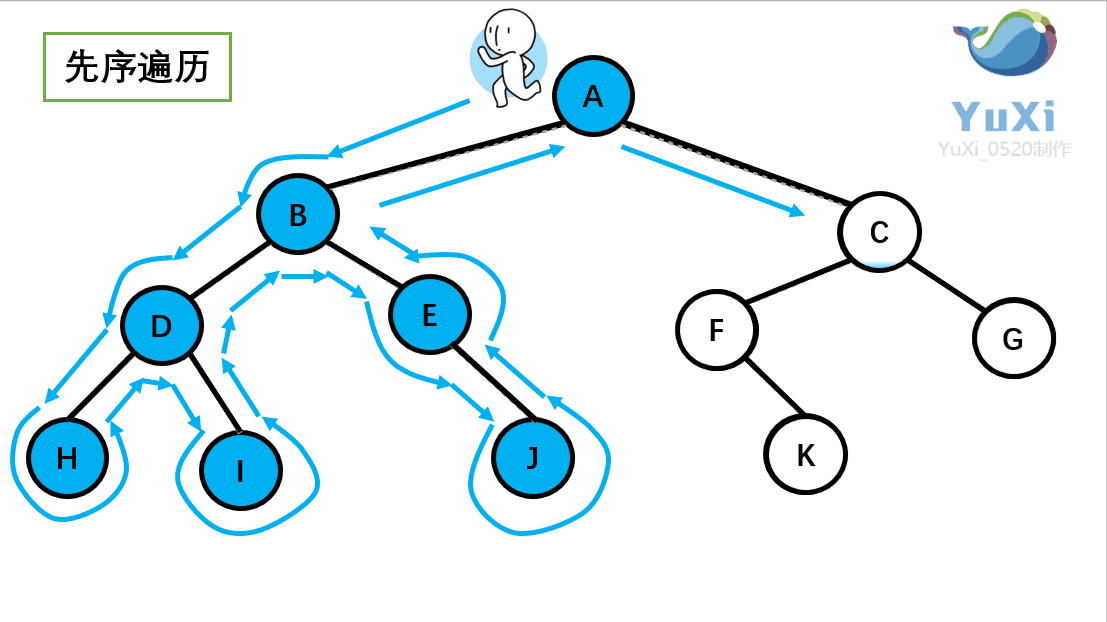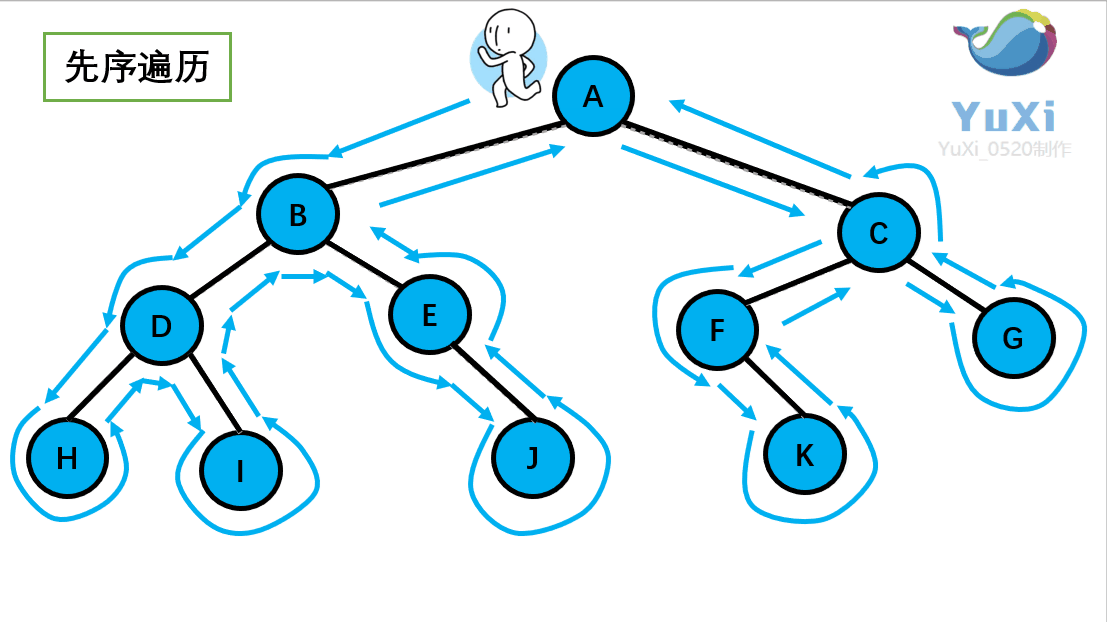
(1).先序遍历可以想象为,一个小人从一棵二叉树根节点为起点,沿着二叉树外沿,逆时针走一圈回到根节点,路上遇到的元素顺序,就是先序遍历的结果
代码解释:
void PrevOrder(BTNode* root) {if (root == NULL){printf("NULL ");return;}printf("%c ", root->data);PrevOrder(root->left);PrevOrder(root->right); }
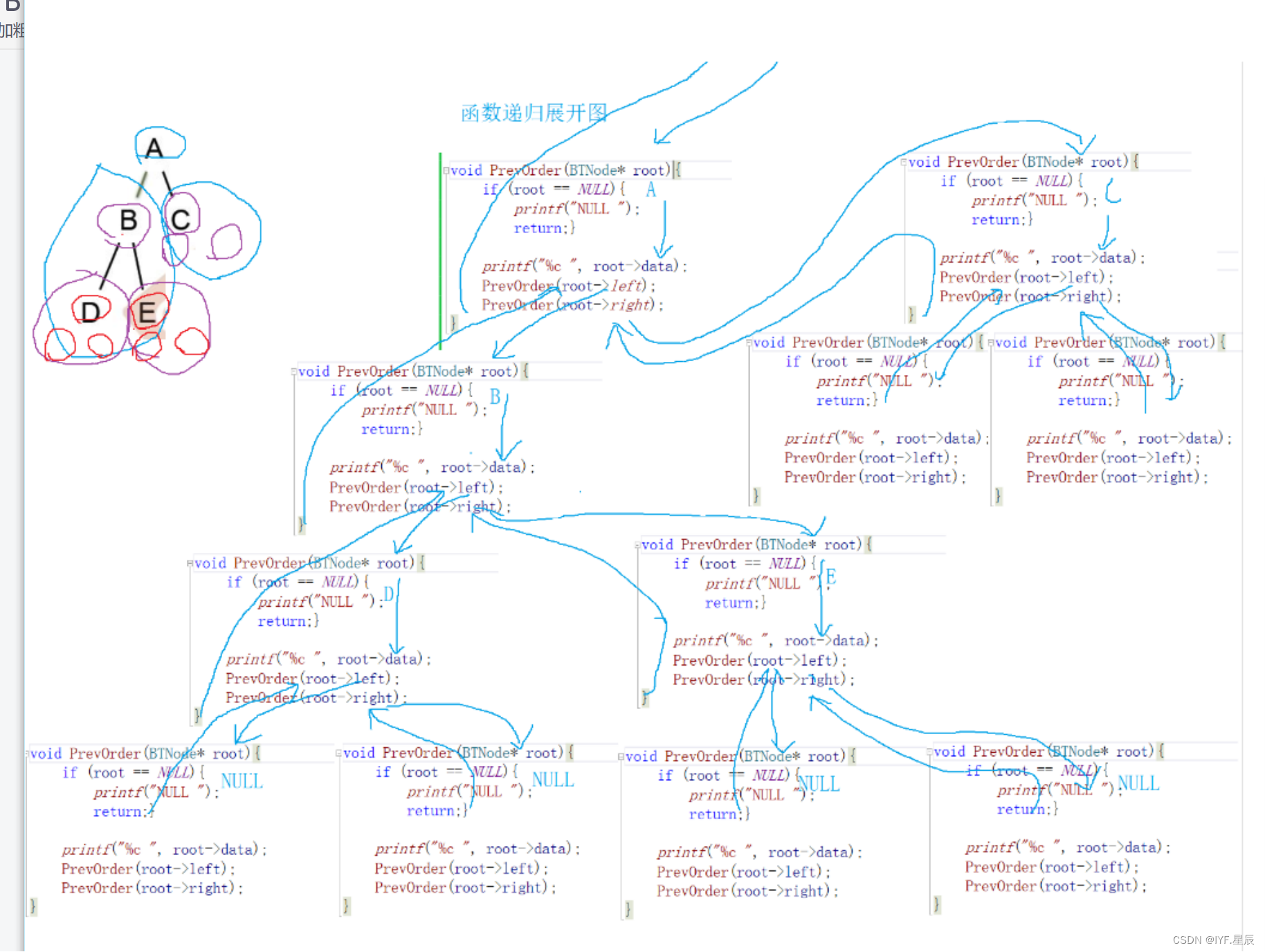
根,PrevOrder(root->left) 后PrevOrder(root->right). 即 根->左子树->右子树 的形式进行遍历。函数进行递推,直到把程序化为不可再分的小的字程序。后回溯依次打印对应数据信息(root->data).
二叉树的中序遍历:
(2).中序遍历可以看成,二叉树每个节点,垂直方向投影下来(可以理解为每个节点从最左边开始垂直掉到地上),然后从左往右数,得出的结果便是中序遍历的结果
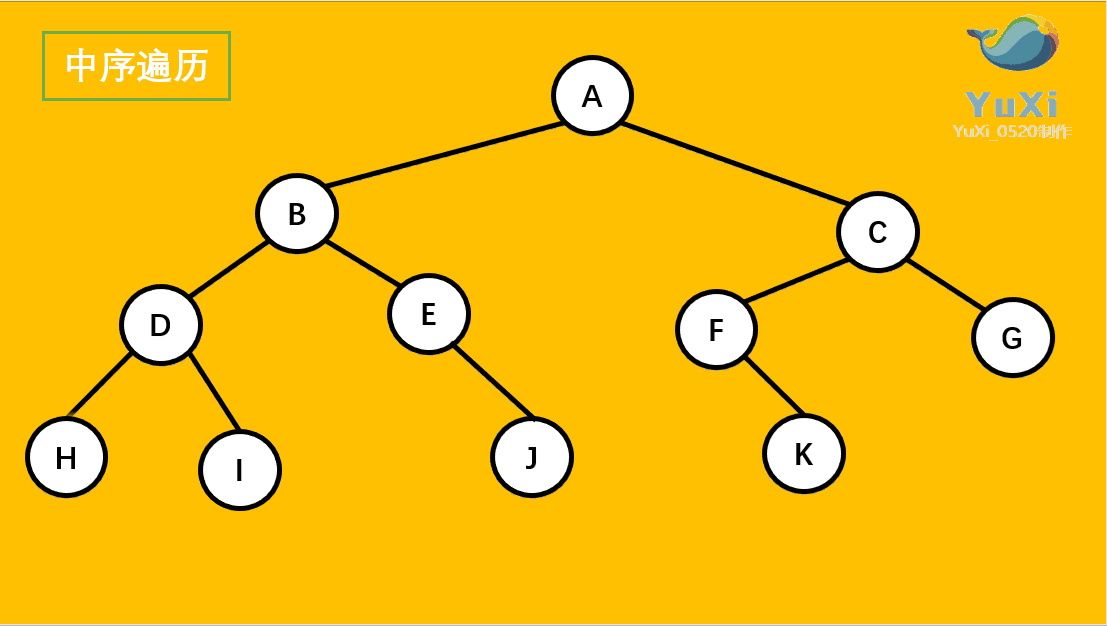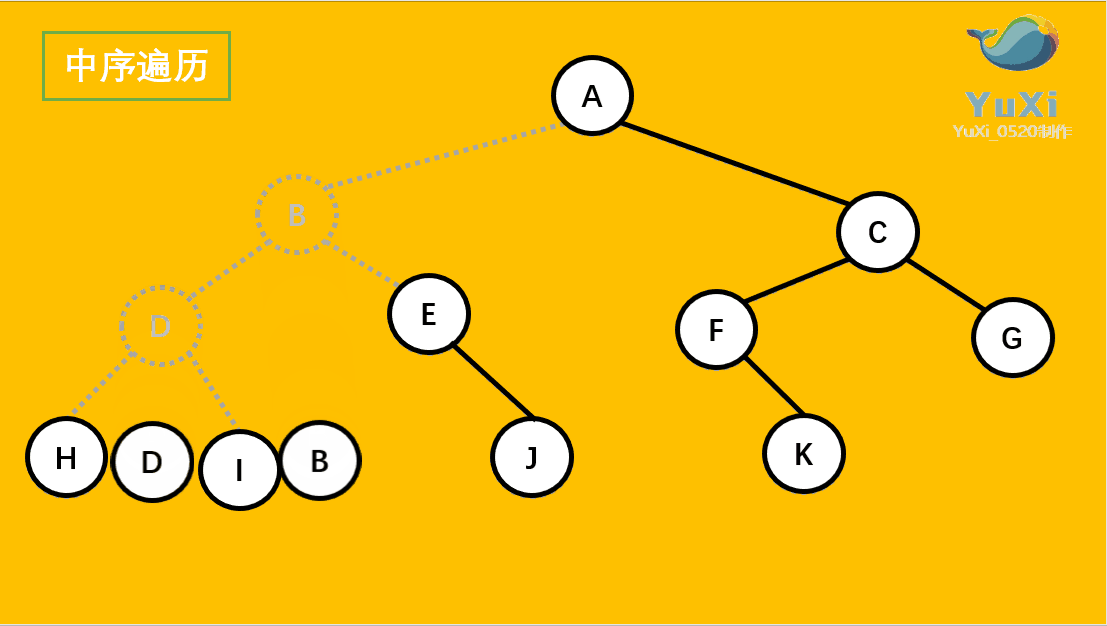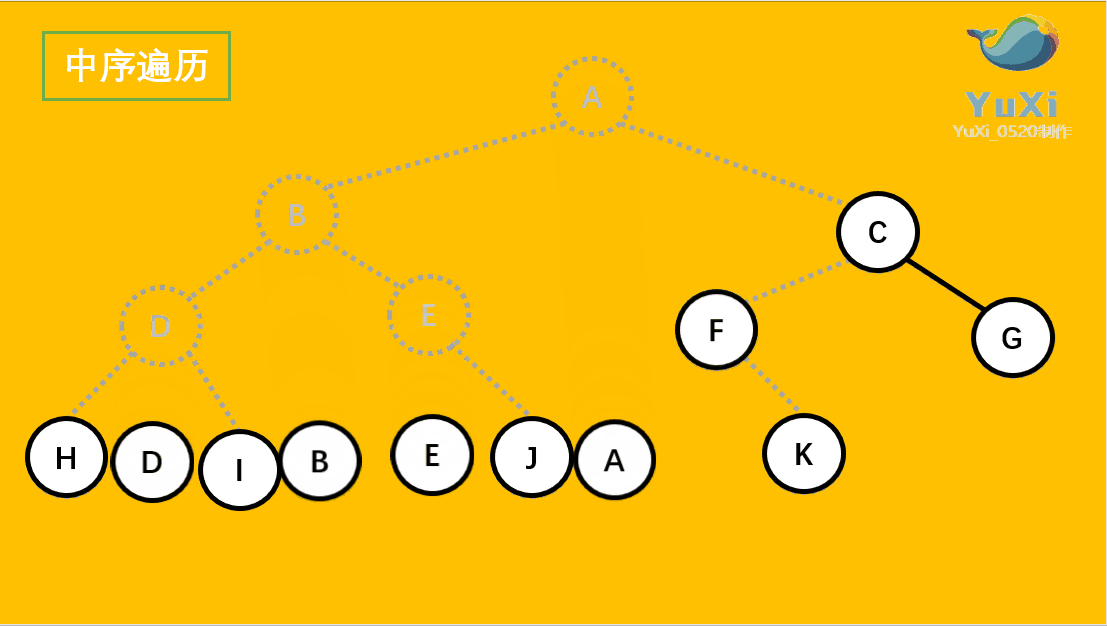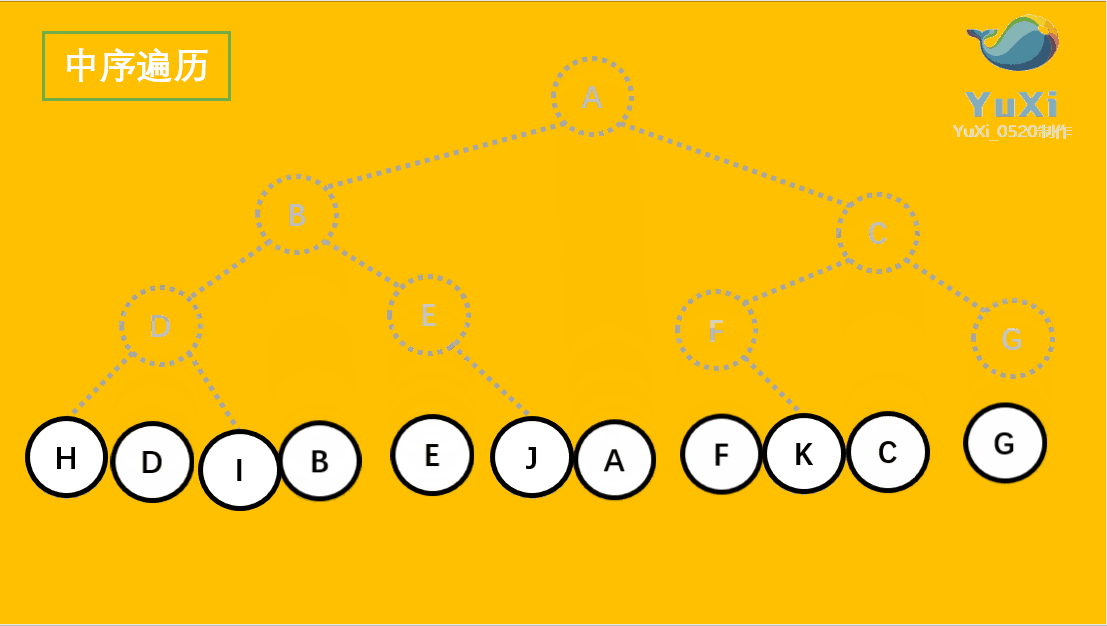
代码解释:
void InOrder(BTNode* root) {if (root == NULL){printf("NULL ");return;}InOrder(root->left);printf("%c ", root->data);InOrder(root->right); }
函数递归展开图与二叉树先序遍历类似.,这里就不在重复说明.
InOrder(root->left) 根 Inorder(root->right);即 左子树 根 右子树 的形式
二叉树的后序遍历:
(3).后序遍历就像是剪葡萄,我们要把一串葡萄剪成一颗一颗的。如果发现一剪刀就能剪下的葡萄(必须是一颗葡萄)(也就是葡萄要一个一个掉下来,不能一口气掉超过1个这样),就把它剪下来,组成的就是后序遍历了。
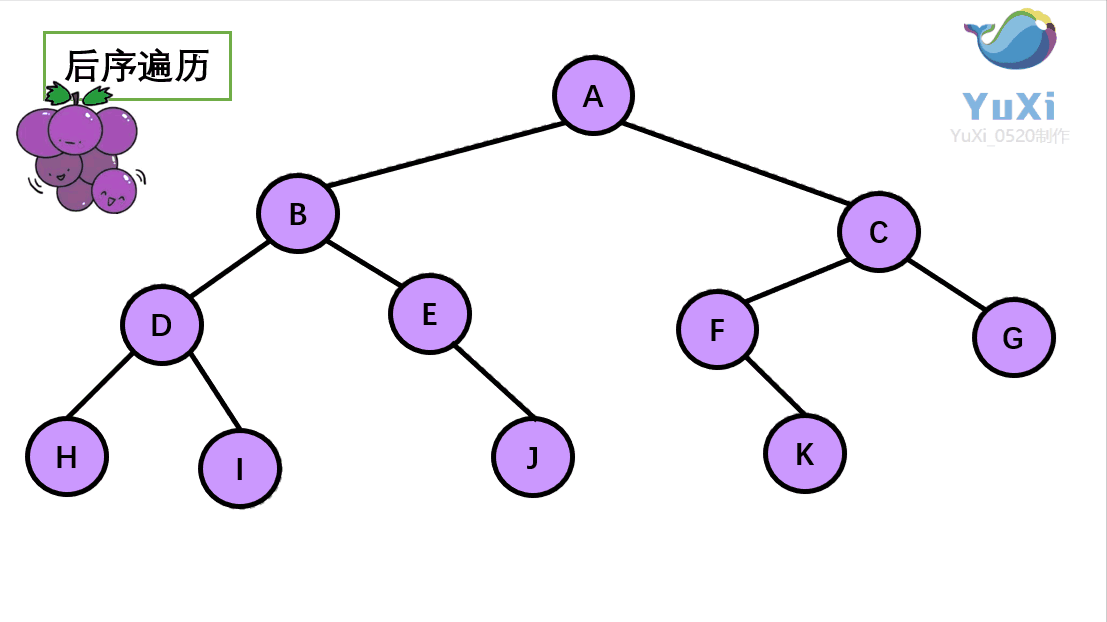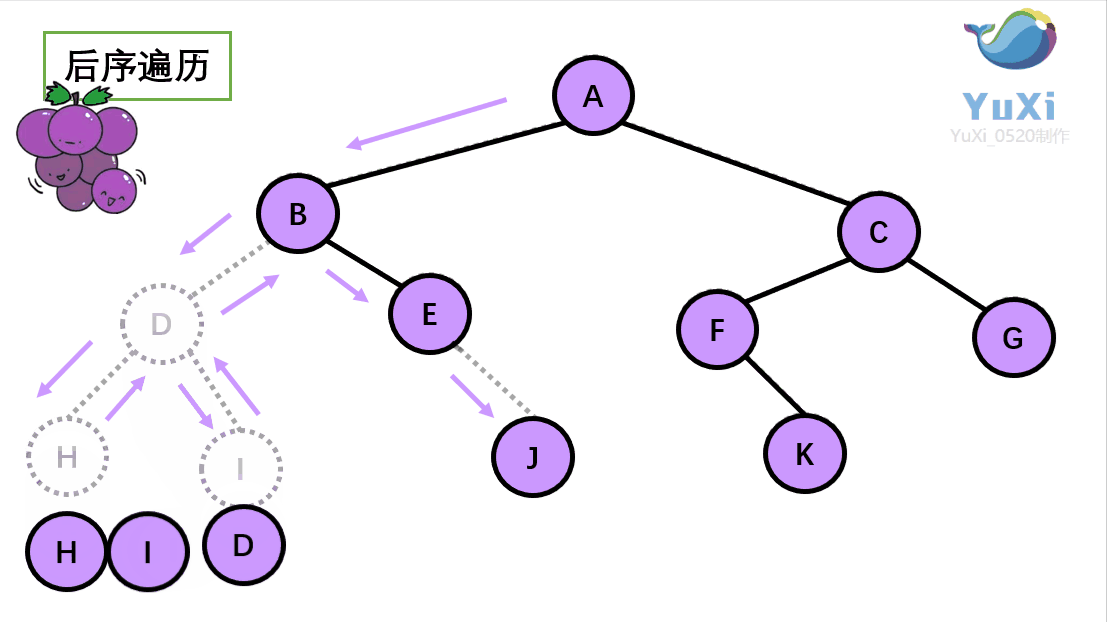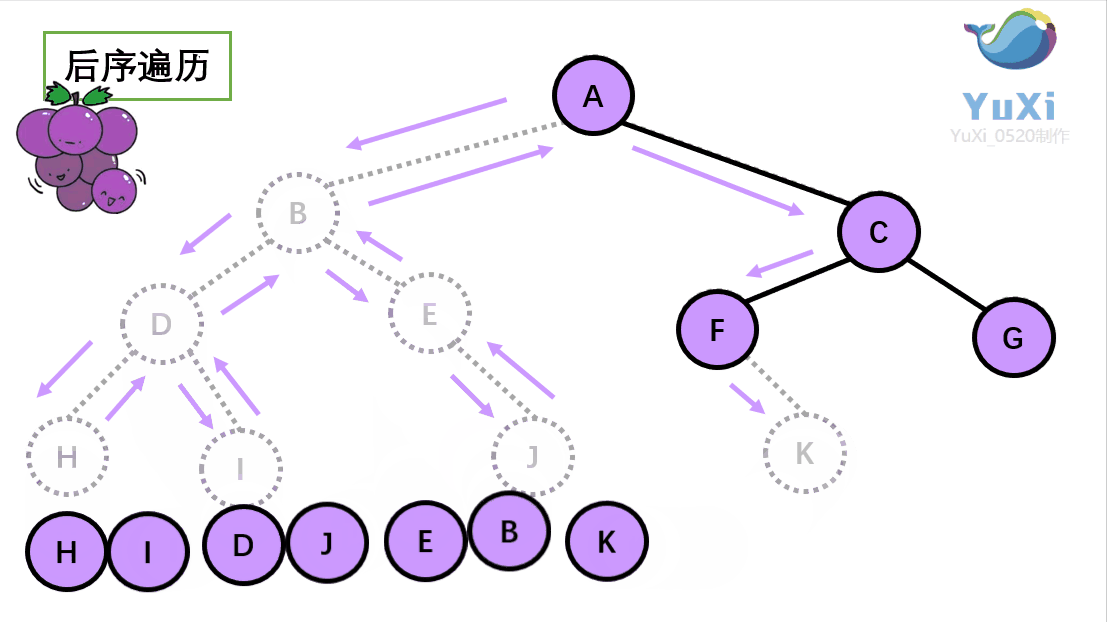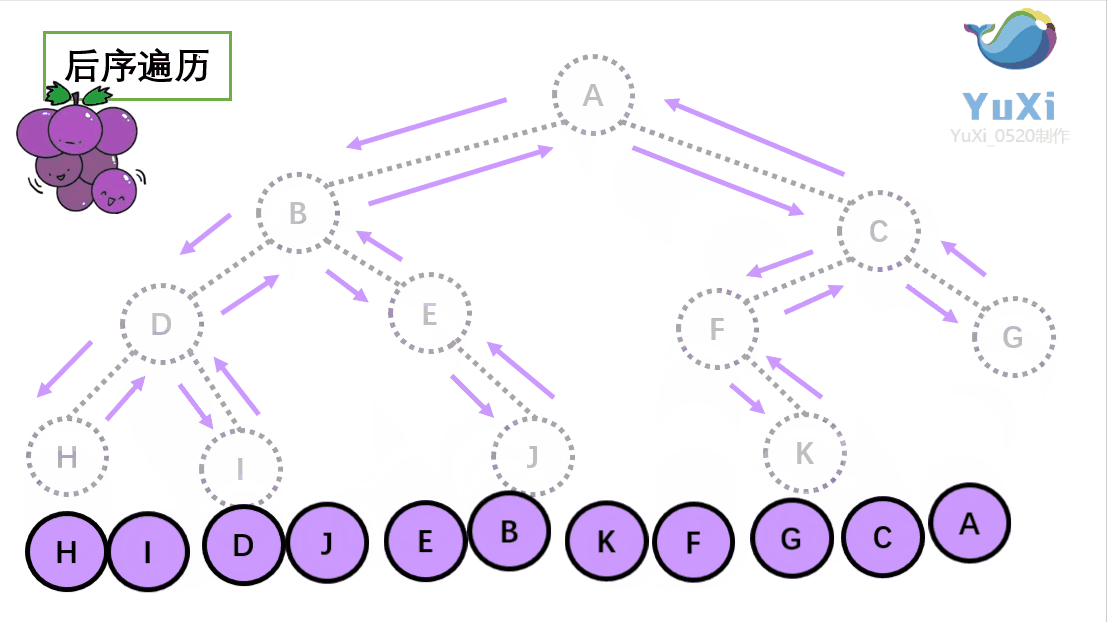
代码解释:
void PostOrder(BTNode* root) {if (root == NULL){printf("NULL ");return;}PostOrder(root->left);PostOrder(root->right);printf("%c ", root->data); }
PostOrder(root->left) PostOrder(root->right) 根;即 左子树 右子树 根 的形式
二叉树的层序遍历:
顾名思义,就是一层一层的进行遍历。
图解:
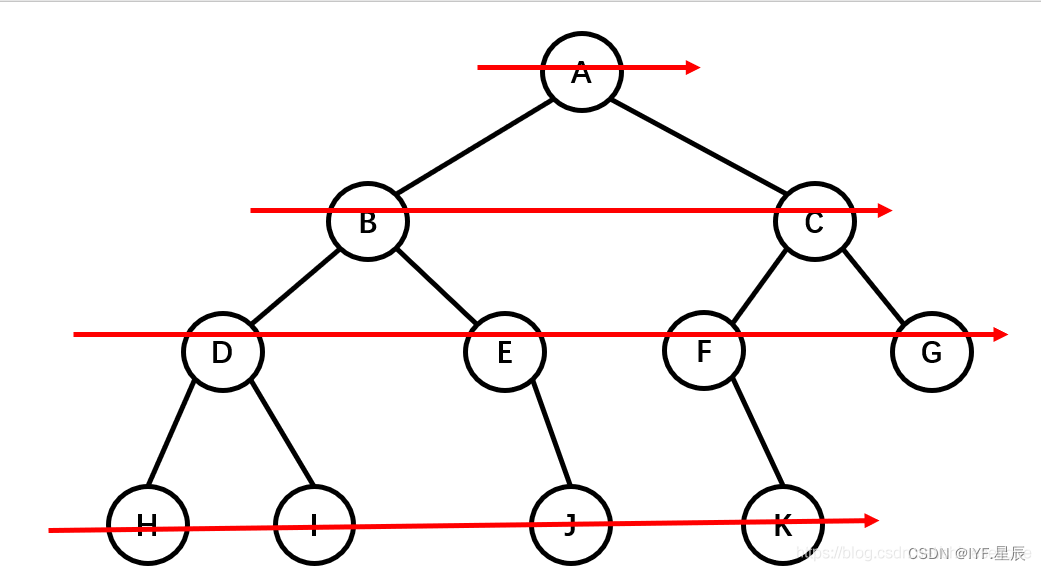
这里用到的队列先进先出的思想,核心思路就是上一层带下一层。如A先进队列,接着A出队列,带着B和C依次进队列,B出带DE,C出带FG……以此类推。
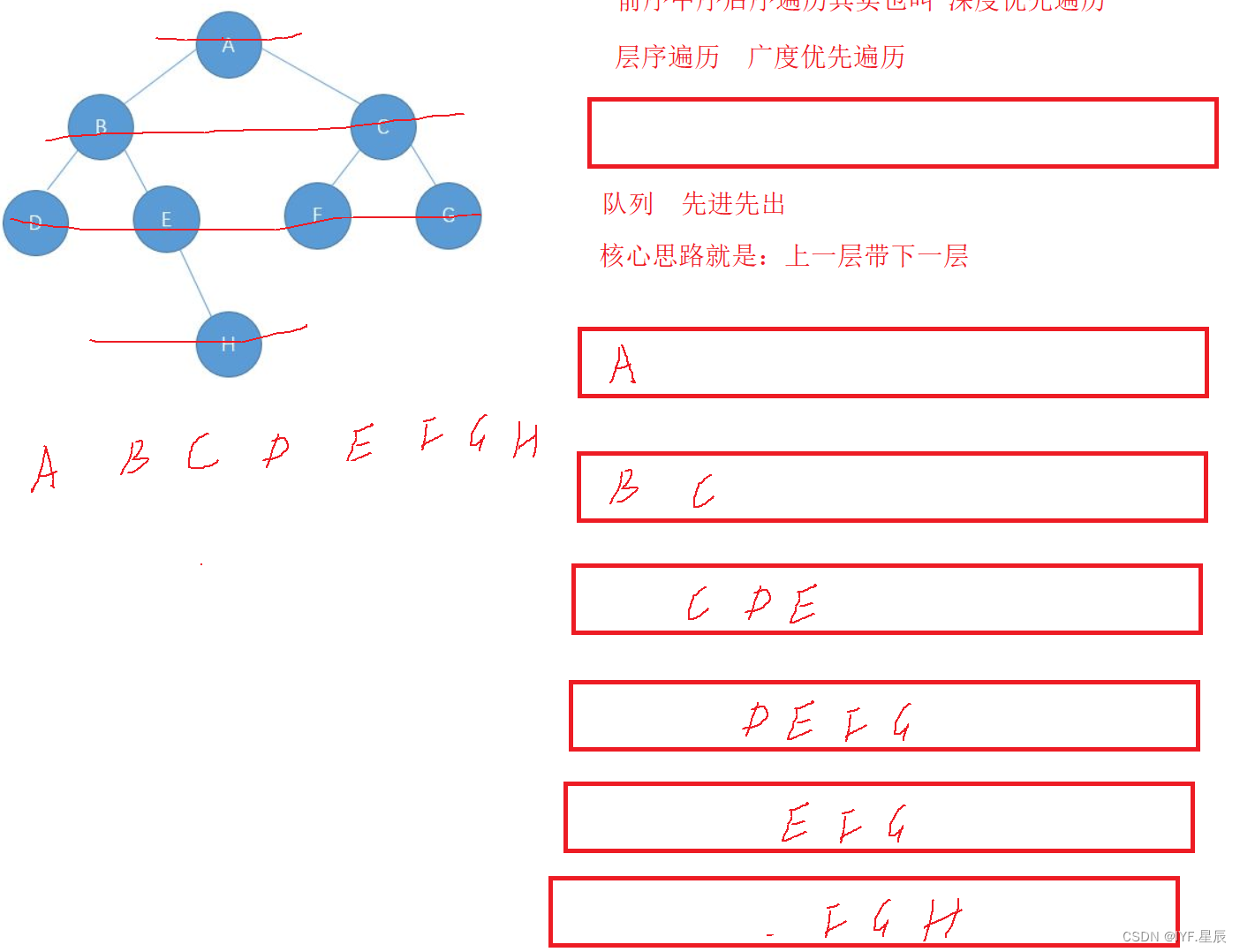
代码解释:
void LevelOrder(BTNode* root) {Queue q;QueueInit(&q);if (root)QueuePush(&q, root);while (!QueueEmpty(&q)){BTNode* front = QueueFront(&q);QueuePop(&q);printf("%c ", front->data);if (front->left){QueuePush(&q, front->left);}if (front->right){QueuePush(&q, front->right);}}printf("\n");QueueDestory(&q); }
初始化队列后,依次按上述的方式入数据和删除数据,最后就能得到相应的序列

二叉树的节点个数:
int TreeSize3(BTNode* root)
{return root == NULL ? 0 : TreeSize3(root->left) + TreeSize3(root->right) + 1;
}
分为最小的子程序即根的左右子树节点个数加本身。
也就是 TreeSize3(root->left)+TreeSize3(root->right)+1;
二叉树叶节点个数:
int TreeLeafSize(BTNode* root)
{if (root == NULL)return 0;if (root->left == NULL && root->right == NULL)return 1;return TreeLeafSize(root->left) + TreeLeafSize(root->right);
}最后完整代码:
#include<stdio.h>
#include<stdlib.h>#include"Queue.h"typedef int BTDataType;
typedef struct BinaryTreeNode
{struct BinaryTreeNode* left;struct BinaryTreeNode* right;BTDataType data;
}BTNode;void PrevOrder(BTNode* root)
{if (root == NULL){printf("NULL ");return;}printf("%c ", root->data);PrevOrder(root->left);PrevOrder(root->right);
}void InOrder(BTNode* root)
{if (root == NULL){printf("NULL ");return;}InOrder(root->left);printf("%c ", root->data);InOrder(root->right);
}void PostOrder(BTNode* root)
{if (root == NULL){printf("NULL ");return;}PostOrder(root->left);PostOrder(root->right);printf("%c ", root->data);
}
int size = 0;
void TreeSize1(BTNode* root)
{if (root == NULL){return;}else size++;TreeSize1(root->left);TreeSize1(root->right);
}void TreeSize2(BTNode* root,int* psize)
{if (root == NULL)return;else{++(*psize);}TreeSize2(root->left,psize);TreeSize2(root->right, psize);
}int TreeSize3(BTNode* root)
{return root == NULL ? 0 : TreeSize3(root->left) + TreeSize3(root->right) + 1;
}int TreeLeafSize(BTNode* root)
{if (root == NULL)return 0;if (root->left == NULL && root->right == NULL)return 1;return TreeLeafSize(root->left) + TreeLeafSize(root->right);
}void LevelOrder(BTNode* root)
{Queue q;QueueInit(&q);if (root)QueuePush(&q, root);while (!QueueEmpty(&q)){BTNode* front = QueueFront(&q);QueuePop(&q);printf("%c ", front->data);if (front->left){QueuePush(&q, front->left);}if (front->right){QueuePush(&q, front->right);}}printf("\n");QueueDestory(&q);
}int main()
{BTNode* A = (BTNode*)malloc(sizeof(BTNode));A->data = 'A';A->left = NULL;A->right = NULL;BTNode* C = (BTNode*)malloc(sizeof(BTNode));C->data = 'C';C->left = NULL;C->right = NULL;BTNode* B = (BTNode*)malloc(sizeof(BTNode));B->data = 'B';B->left = NULL;B->right = NULL;BTNode* D = (BTNode*)malloc(sizeof(BTNode));D->data = 'D';D->left = NULL;D->right = NULL;BTNode* E = (BTNode*)malloc(sizeof(BTNode));E->data = 'E';E->left = NULL;E->right = NULL;A->left = B;A->right = C;B->left = D;B->right = E;PrevOrder(A);printf("\n");PostOrder(A);printf("\n");LevelOrder(A);printf("TreeLeafSize:%d\n", TreeLeafSize(A));printf("TreeSize:%d\n", TreeSize3(A));printf("TreeSize:%d\n", TreeSize3(B));return 0;
}注意这里TreeSize1,TreeSize2,TreeSize3只是计算二叉树节点个数的三种方法。
这里创建的二叉树为:
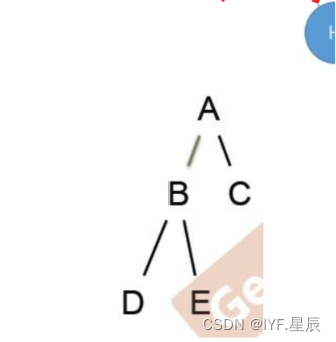
运行结果:
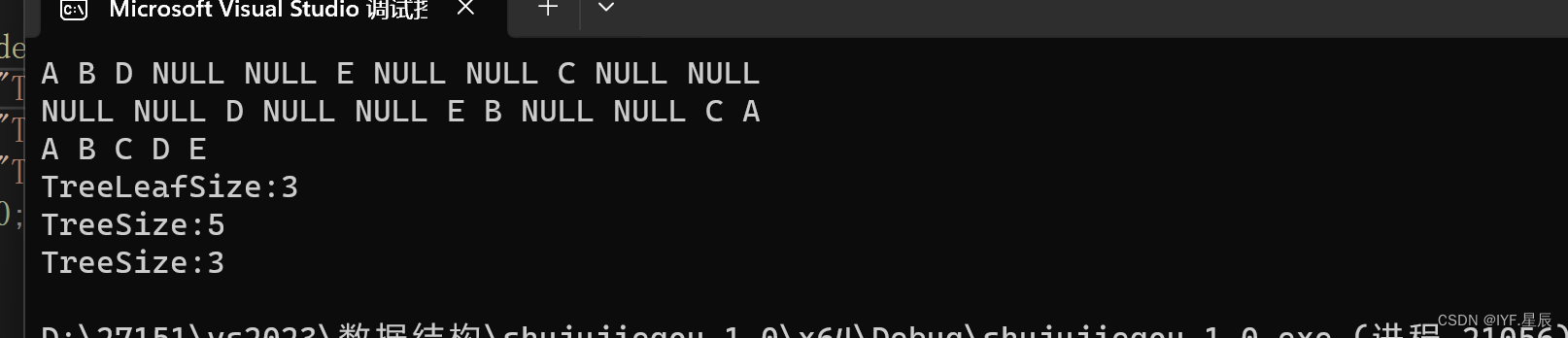
博客到这里也是结束了,喜欢的小伙伴可以点赞加关注支持下博主,这对我真的很重要~~

相关文章:

数据结构——二叉树(先序、中序、后序及层次四种遍历(C语言版))超详细~ (✧∇✧) Q_Q
目录 二叉树的定义: *特殊的二叉树: 二叉树的性质: 二叉树的声明: 二叉树的先序遍历: 二叉树的中序遍历: 二叉树的后序遍历: 二叉树的层序遍历: 二叉树的节点个数: 二叉…...
如何快速打造属于自己的接口自动化测试框架
1 接口测试 接口测试是对系统或组件之间的接口进行测试,主要是校验数据的交换,传递和控制管理过程,以及相互逻辑依赖关系。 接口自动化相对于UI自动化来说,属于更底层的测试,这样带来的好处就是测试收益更大ÿ…...

人工智能在数据安全中的应用场景
场景一:数据资产梳理 数据资产梳理是数据安全的基础。知道企业究竟有多少数据,这些数据在哪里?有哪些类型的数据?其中哪些是敏感数据?这些数据的敏感等级分别是什么?只有明确了保护的目标,才能…...

2024.1.16每日一题
LeetCode 2719.统计整数数目 2719. 统计整数数目 - 力扣(LeetCode) 题目描述 给你两个数字字符串 num1 和 num2 ,以及两个整数 max_sum 和 min_sum 。如果一个整数 x 满足以下条件,我们称它是一个好整数: num1 &l…...
python入门,数据容器的通用操作(len,max,min,sorted)
1.len统计容器内元素个数 2.max统计元素最大元素 3.min统计元素最小元素 4.容器的转化功能 list(容器)将给定容器转化为列表 字符串转列表将字符串内的每一个元素都取了出来作为列表的每一个元素 字典则只会取出它的key,value会消失 str&…...
运筹说 第67期 | 动态规划模型的建立与求解
通过前一期的学习,我们已经学会了动态规划的基本概念和基本原理。本期小编带大家学习动态规划模型的建立与求解。 动态规划模型的建立 一 概述 建立动态规划的模型,就是分析问题并建立问题的动态规划基本方程。 成功地应用动态规划方法的关键&#x…...

大模型压缩与优化的技术原理与创新方法
目录 前言1 模型压缩简介2 知识蒸馏3 模型剪枝3.1 结构化剪枝3.2 非结构化剪枝 4 模型量化4.1 浮点表示 vs 定点表示4.2 位数选择与性能影响4.3 量化技术 5 其他模型压缩方法5.1 Weight Sharing: 参数共享5.2 Low-rank Approximation: 低秩分解5.3 Architecture Search: 神经网…...
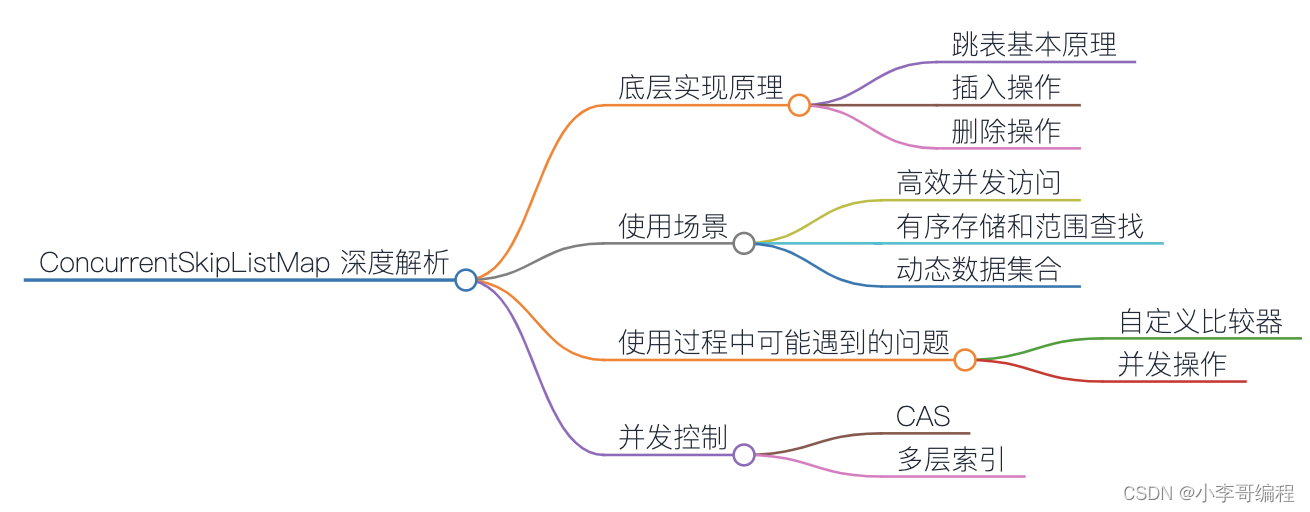
ConcurrentSkipListMap 深度解析
ConcurrentSkipListMap是Java集合框架中的一员,它实现了ConcurrentNavigableMap接口,基于跳表(Skip List)实现,并提供了高效的并发控制。在本文中,我们将深入研究ConcurrentSkipListMap的底层实现原理、适用…...

Vue学习笔记6--配置代理
一、axios Axios 是一个基于 promise 网络请求库,作用于node.js 和浏览器中。 它是 isomorphic 的(即同一套代码可以运行在浏览器和node.js中)。在服务端它使用原生 node.js http 模块, 而在客户端 (浏览端) 则使用 XMLHttpRequests。 二、配置代理 1. 方法一 在…...
-C++和QT编程第三天-C++类和对象高级应用(物联技术666))
嵌入式培训机构四个月实训课程笔记(完整版)-C++和QT编程第三天-C++类和对象高级应用(物联技术666)
链接:https://pan.baidu.com/s/1YRXI0WiABUlYaQXQDNfbyA?pwd=1688 提取码:1688 上午:类和对象高级应用(续) 下午:派生和继承 教学内容: 1、友元 类的私有成员只能在类定义的范围内使用,也就是说私有成员只能通过它的成员函数来访问但是,有时候需要在类的外部访问…...
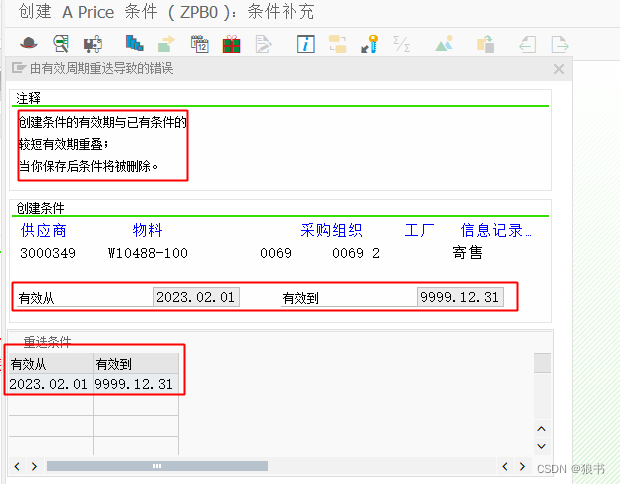
SAP中采购文档价格条件可以删除吗?
首先要声名,基于采购价格条件的严谨性和历史追朔需求,删除属于危险操作。不建议普通用户去执行操作。如果有兴趣,在测试系统中自行测试一下即可。正式系统中,还请慎重处理。 笔者公司日常不会去删除采购价格,日常处理…...
)
Baumer工业相机堡盟工业相机如何通过NEOAPI SDK设置硬件触发模式(C++)
Baumer工业相机堡盟工业相机如何通过NEOAPI SDK设置硬件触发模式(C) Baumer工业相机Baumer工业相机NEOAPI SDK和硬件触发模式的技术背景Baumer工业相机通过BGAPISDK设置硬件触发模式功能1.引用合适的类文件2.通过BGAPISDK在Line0上施加12V/24V电压信号实…...
-Linux网络编程第二天-tcp编程练习(物联技术666))
嵌入式培训机构四个月实训课程笔记(完整版)-Linux网络编程第二天-tcp编程练习(物联技术666)
点赞+关注,功德无量。更多配套资料,欢迎私信。 网盘链接:百度网盘 请输入提取码 WebServer编程: -------------------------------------- #include <stdio.h> #include <stdlib.h> #include <string.h> #i…...

【IC前端虚拟项目】MVU子模块DS文档编写与注意事项
【IC前端虚拟项目】数据搬运指令处理模块前端实现虚拟项目说明-CSDN博客 DS文档顾名思义就是Design Specification,设计规格文档,对应的就是我们实际一个模块的设计思路和细节: DS - Design Specification(设计规格):"DS" 表示设计规格,它是在架构规格之后,…...
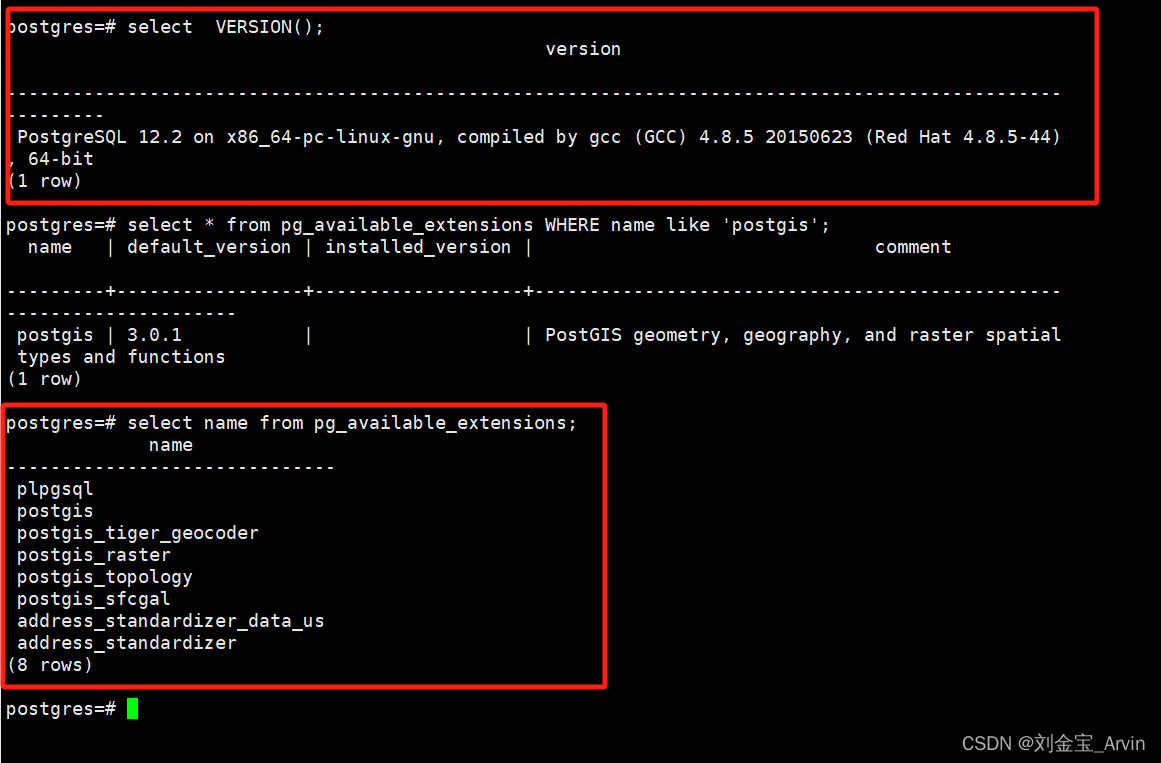
Postgresql 12.2 + PostGIS 3.0.1 安装部署
参考文档: 按照该文档安装即可,如果遇到报错,可以参考下文: https://blog.csdn.net/weixin_41166785/article/details/127674169 所需的安装包 在资源里面(我看下怎么可以不用积分下载) 1、no acceptable…...
MAC iterm 显示git分支名
要在Mac上的iTerm中显示Git分支名,您需要使用一个名为“Oh My Zsh”的插件。Oh My Zsh是一个流行的Zsh框架,它提供了许多有用的功能和插件,包括在终端中显示Git分支名。 以下是在iTerm中显示Git分支名的步骤: 1、安装Oh My Zsh&…...

智慧公厕:利用物联网、云计算和人工智能实现智能化管理与控制
智慧公厕是指利用传感感知、物联网、互联网、大数据、云计算、自动化控制等先进技术,实现对公厕的智能化管理与控制。通过以上高精尖的信息技术手段,可以实时监测厕所内人体活动状态、人体存在状态、空气质量情况、环境变化情况、设施设备运行状态等信息…...

【漏洞复现】Apache Tomcat AJP文件包含漏洞(CVE-2020-1938)
Nx01 产品简介 Apache Tomcat 是一个免费的开源 Web 应用服务器,在中小型企业和个人开发用户中有着广泛的应用。 Nx02 漏洞描述 默认情况下,Apache Tomcat会开启AJP连接器,由于AJP服务(8009端口)存在文件包含缺陷&…...
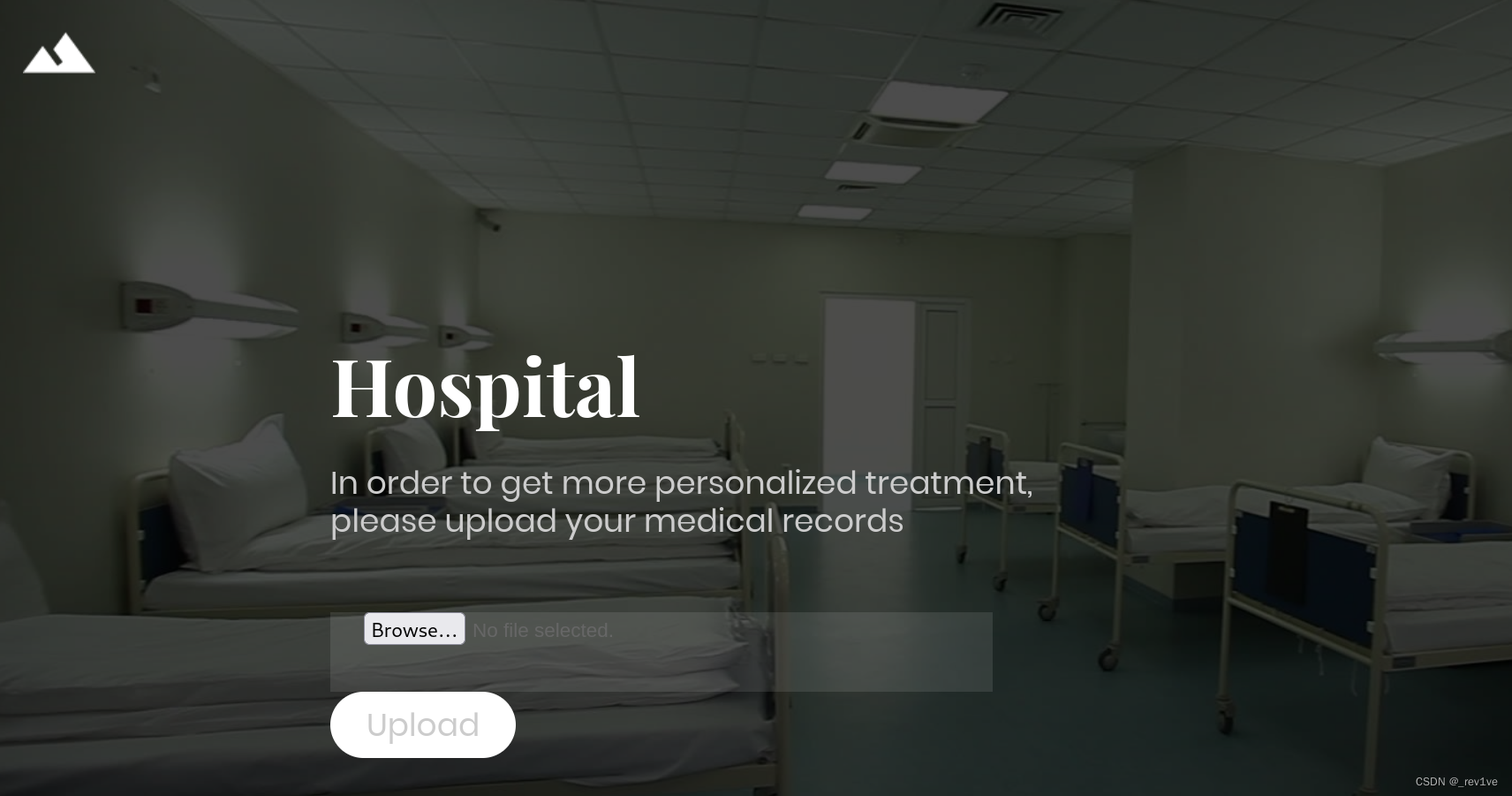
[渗透测试学习] Hospital - HackTheBox
文章目录 信息搜集getshell提权信息搜集 nmap扫描一下端口 发现8080端口和443端口有http服务 然后发现3389端口是启用了ms-wbt-server服务 在对443端口的扫描没有收获,并且只有邮箱登录界面无法注册 接着看向8080端口,我们随便注册用户登录后发现有文件上传功能 getshell …...
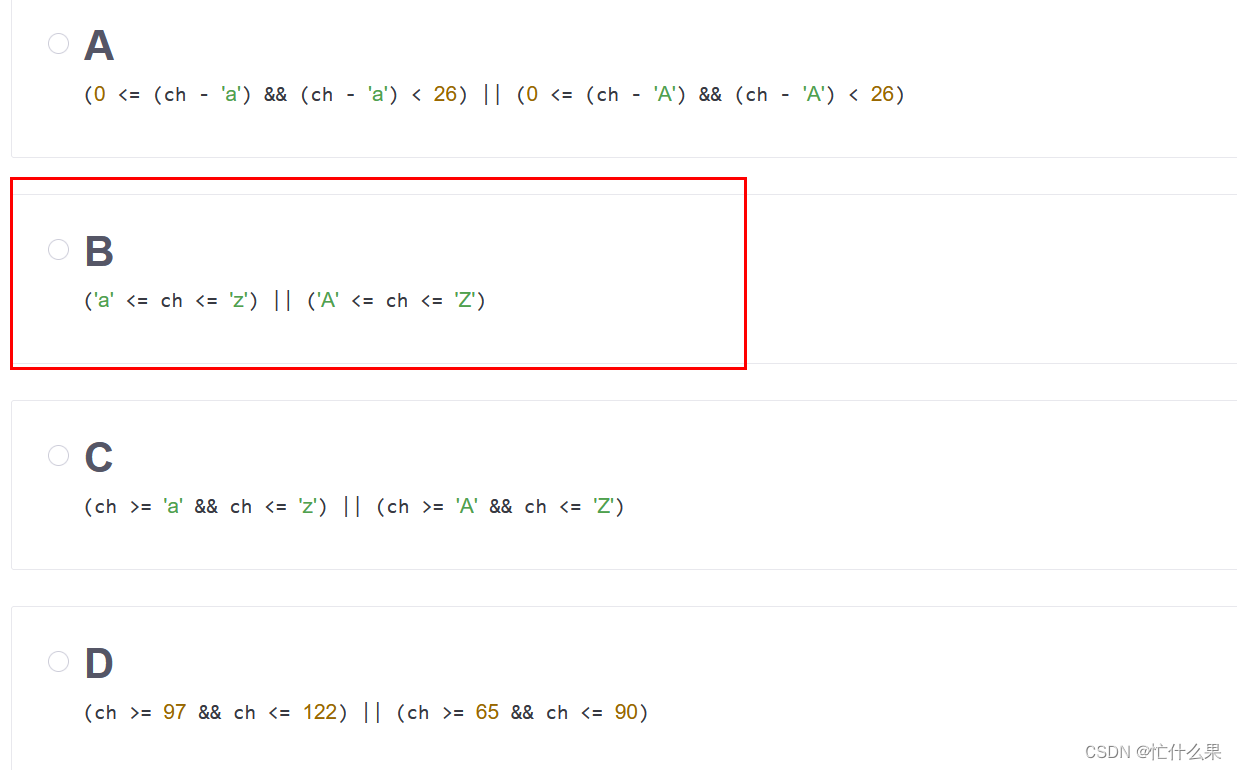
C技能树-学习笔记(1-2)C语言概述和数据类型
参考:https://edu.csdn.net/skill/c 1、输出 “Hello, World!” 字符串,请选出错误答案。 2、错误的print函数。 for … in …:是python的语法,C语言的写法是for (;😉 3、C标准 没有C19标准。 4、了解C编译管道 …...

Flask RESTful 示例
目录 1. 环境准备2. 安装依赖3. 修改main.py4. 运行应用5. API使用示例获取所有任务获取单个任务创建新任务更新任务删除任务 中文乱码问题: 下面创建一个简单的Flask RESTful API示例。首先,我们需要创建环境,安装必要的依赖,然后…...

label-studio的使用教程(导入本地路径)
文章目录 1. 准备环境2. 脚本启动2.1 Windows2.2 Linux 3. 安装label-studio机器学习后端3.1 pip安装(推荐)3.2 GitHub仓库安装 4. 后端配置4.1 yolo环境4.2 引入后端模型4.3 修改脚本4.4 启动后端 5. 标注工程5.1 创建工程5.2 配置图片路径5.3 配置工程类型标签5.4 配置模型5.…...

CVPR 2025 MIMO: 支持视觉指代和像素grounding 的医学视觉语言模型
CVPR 2025 | MIMO:支持视觉指代和像素对齐的医学视觉语言模型 论文信息 标题:MIMO: A medical vision language model with visual referring multimodal input and pixel grounding multimodal output作者:Yanyuan Chen, Dexuan Xu, Yu Hu…...

SciencePlots——绘制论文中的图片
文章目录 安装一、风格二、1 资源 安装 # 安装最新版 pip install githttps://github.com/garrettj403/SciencePlots.git# 安装稳定版 pip install SciencePlots一、风格 简单好用的深度学习论文绘图专用工具包–Science Plot 二、 1 资源 论文绘图神器来了:一行…...

Objective-C常用命名规范总结
【OC】常用命名规范总结 文章目录 【OC】常用命名规范总结1.类名(Class Name)2.协议名(Protocol Name)3.方法名(Method Name)4.属性名(Property Name)5.局部变量/实例变量(Local / Instance Variables&…...

转转集团旗下首家二手多品类循环仓店“超级转转”开业
6月9日,国内领先的循环经济企业转转集团旗下首家二手多品类循环仓店“超级转转”正式开业。 转转集团创始人兼CEO黄炜、转转循环时尚发起人朱珠、转转集团COO兼红布林CEO胡伟琨、王府井集团副总裁祝捷等出席了开业剪彩仪式。 据「TMT星球」了解,“超级…...

C++八股 —— 单例模式
文章目录 1. 基本概念2. 设计要点3. 实现方式4. 详解懒汉模式 1. 基本概念 线程安全(Thread Safety) 线程安全是指在多线程环境下,某个函数、类或代码片段能够被多个线程同时调用时,仍能保证数据的一致性和逻辑的正确性…...

STM32HAL库USART源代码解析及应用
STM32HAL库USART源代码解析 前言STM32CubeIDE配置串口USART和UART的选择使用模式参数设置GPIO配置DMA配置中断配置硬件流控制使能生成代码解析和使用方法串口初始化__UART_HandleTypeDef结构体浅析HAL库代码实际使用方法使用轮询方式发送使用轮询方式接收使用中断方式发送使用中…...

【堆垛策略】设计方法
堆垛策略的设计是积木堆叠系统的核心,直接影响堆叠的稳定性、效率和容错能力。以下是分层次的堆垛策略设计方法,涵盖基础规则、优化算法和容错机制: 1. 基础堆垛规则 (1) 物理稳定性优先 重心原则: 大尺寸/重量积木在下…...

DiscuzX3.5发帖json api
参考文章:PHP实现独立Discuz站外发帖(直连操作数据库)_discuz 发帖api-CSDN博客 简单改造了一下,适配我自己的需求 有一个站点存在多个采集站,我想通过主站拿标题,采集站拿内容 使用到的sql如下 CREATE TABLE pre_forum_post_…...
