开关电源环路稳定性分析(10)——OPA和OTA型补偿器传递函数
大家好,这里是大话硬件。
在前面9讲的内容中将开关电源环路分析进行了梳理,我相信很多人即使都看完了,应该还是不会设计,而且还存在几个疑问。比如我随便举几个:
开关电源的带宽怎么设定?开关电源精度和什么相关?怎么调节动态响应?动态响应和什么有关系等等。
我在学习的过程中也一样,对这部分内容充满了疑问。因此,后面关于环路分析的内容,主要是针对开关电源系统中比较难理解的,常见的,经常在设计产品时遇到的问题,进行再一次的分析。
这里非常欢迎大家留言提出疑问,我会针对这些疑问专门写文章来分析。
1.OPA型补偿网络
在前面推导OPA环路传递函数使用的拓扑如下
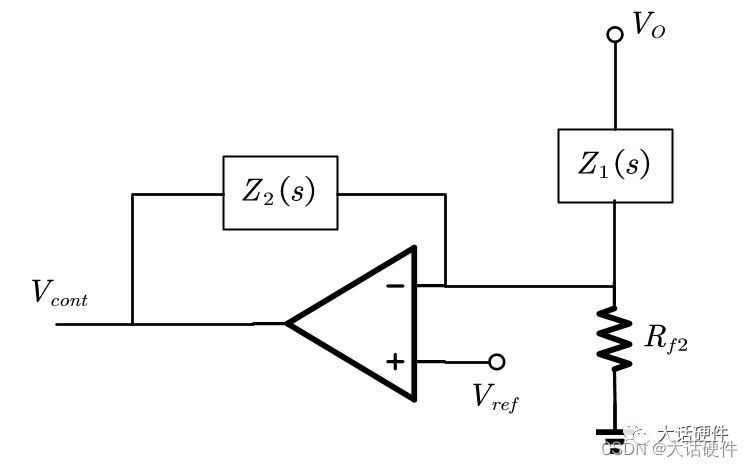
推导过程:
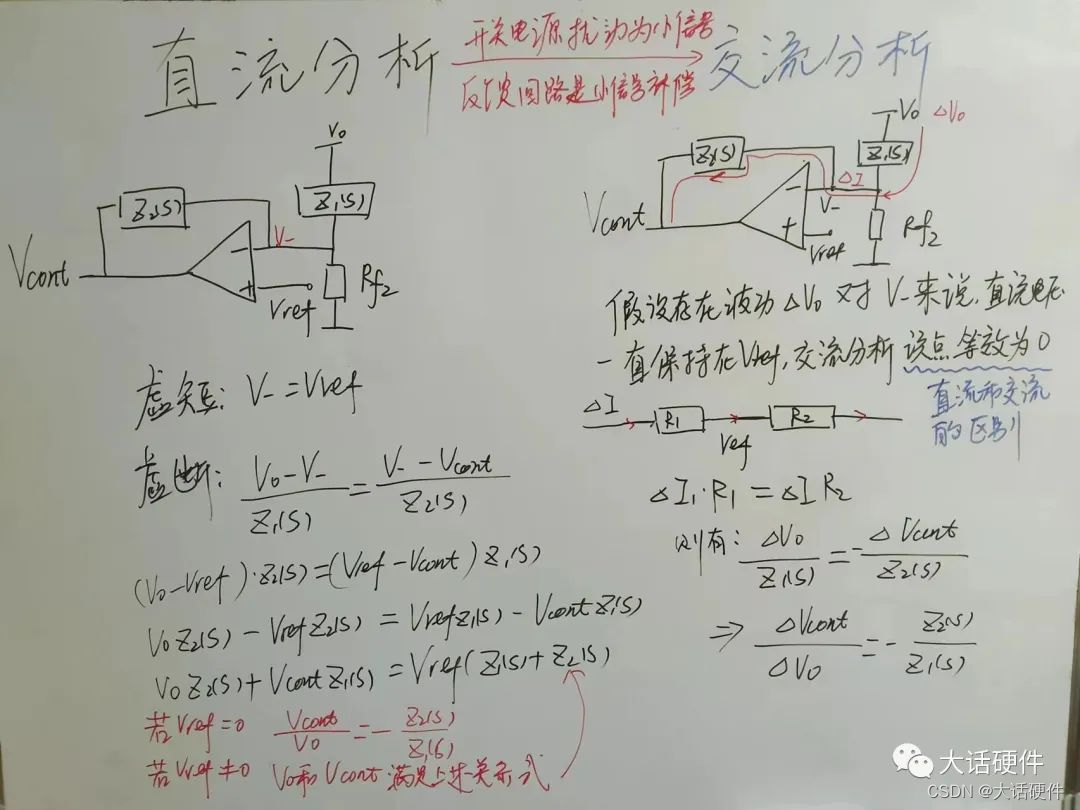
疑问1:为什么传递函数中下分压电阻没参与传递函数?
2.OTA型补偿网络
在前面推导OTA型环路传递时,使用的拓扑如下
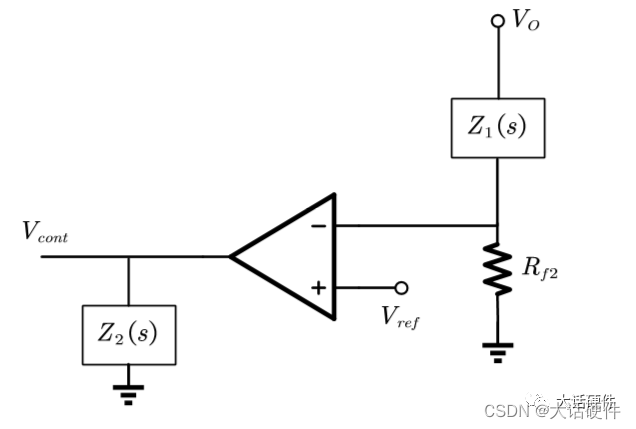
推导过程:
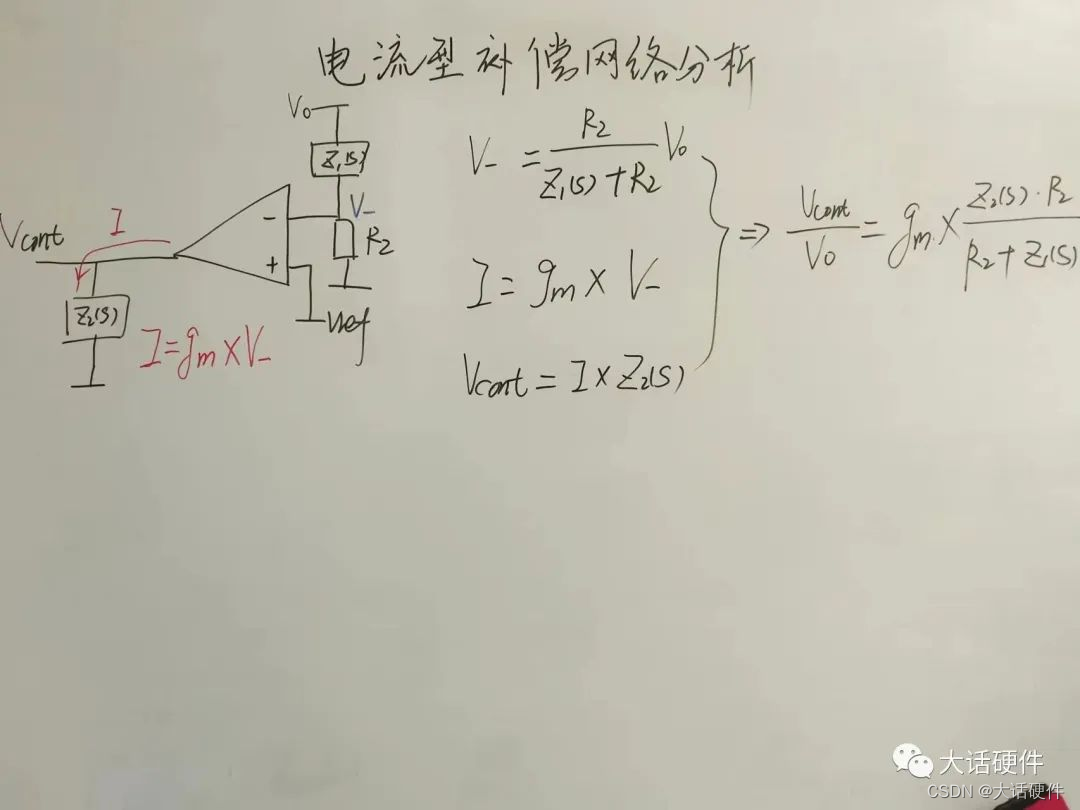
疑问2:为什么传递函数中下分压电阻参与了传递函数?
不知道大家如何看待上面OPA型和OTA型这两种差异,或者是如何理解这种差异。反正我在推导的理解的过程中产生了这样的疑问。
虽然从结果看,这样的分析确实是对的,但是深层次的原因是什么,如何解释,下面将重点分析。
理解思路1:从电路理论的角度来分析
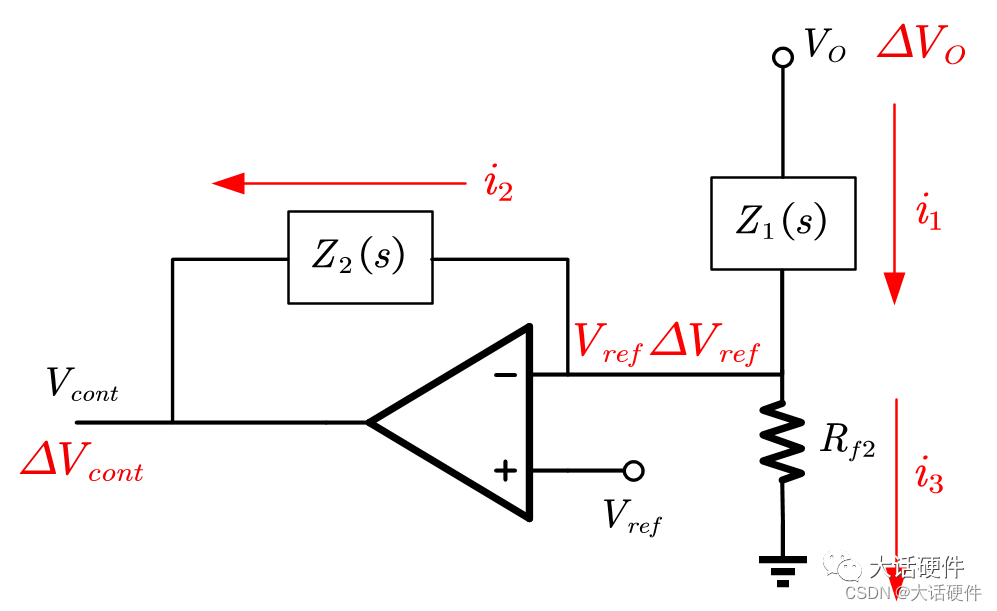
假设输出电压Vout由于负载的波动存在电压变化,用ΔVo来表示,此时会在Z1上流过一定的电流,在Rf2上流过一定的电流,还有一部分电流流过Z2。因此根据基尔霍夫定律可知:
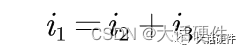
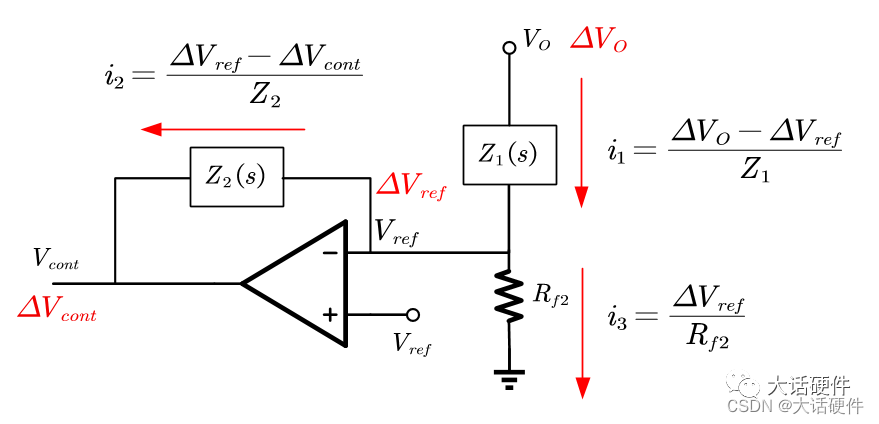
使用运算放大器作为补偿器件,而且是负反馈的形式,那么就存在虚短和虚断的特性。这是因为运放的开环增益Aol无穷大,加上负反馈的存在,必须有正相端的电压和负相端的电压相等。
根据虚断:可以证明上述基尔霍夫定律是成立的;
根据虚短:在负相端的电压会保持一直和正相端的电压相同,也就是Vref的值,而Vref的值无论是直流还是交流,都一直保持不变,所以:
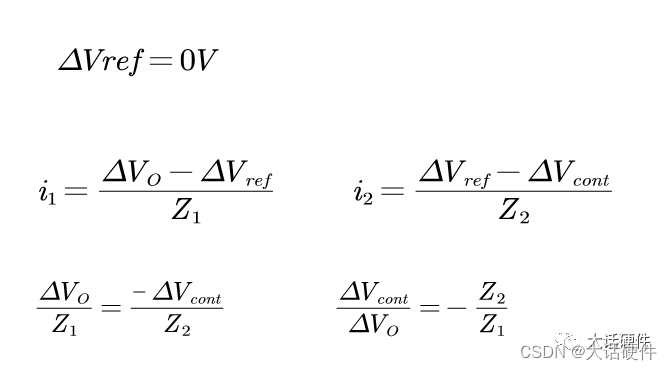
理解思路2:从叠加定理的角度来分析
在OPA型的环路补偿拓扑中,有直流电压Vref,且不随频率改变,而环路补偿属于小信号分析,随着频率改变,输出电压Vcont其实既有直流成分,也有交流成分,可以写成下面的表达式:
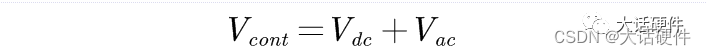
在反馈系统中存在直流电压Vref,交流变化信号Vout,因此,使用叠加定理
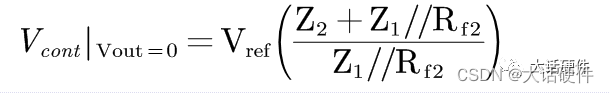
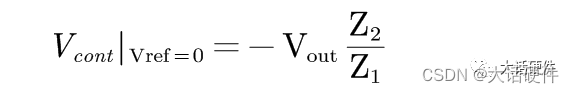
叠加后
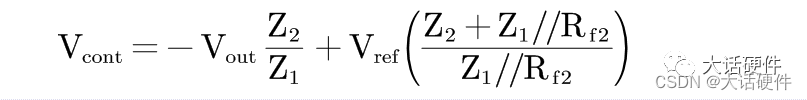
从Vcont的表达式可以看出来,误差放大器输出电压既有直流成分,也有交流成分。我们需要求解的是Vcont和Vout的传递函数。此时可以将上述的函数写成Y=kX+b的形式,对Y求X的微分可以得到:
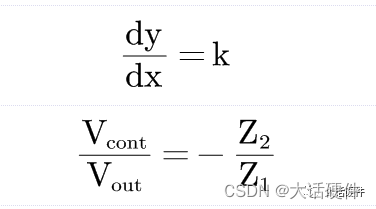
所以,对于OPA型的拓扑来说,无论是从基尔霍夫定律定理的角度还是从叠加定理的角度来分析,下面的电阻Rf2确实没有参与到反馈电路中。但是这个电阻并不是一无是处。设定输出电压值的时候,需要使用这个电阻。
上面的分析解释了为什么OPA型下面的电阻未参与传递函数的求解。
OTA型的拓扑结构如下所示,这种结构的传递函数有R2的参数,这是为什么?
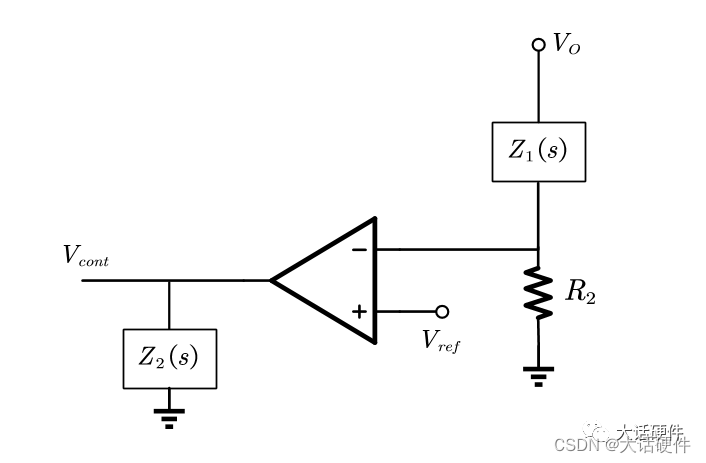
要分析这个原因,需要理解跨导型运算放大器和通用型运算放大器的差异,通用型的运算放大器的开环增益无穷大,运放无论在什么情况下都会调节同相和反相端的电压相等。而跨导型的特性由跨导因子决定Gm,跨导型的运算放大器是一个压控电流源。
内部电路简化等效电路如下:
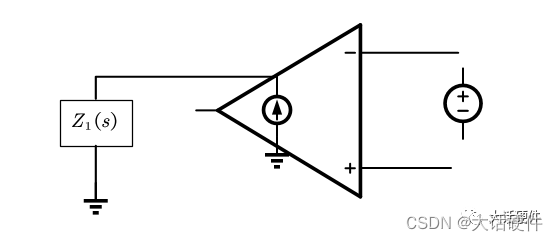
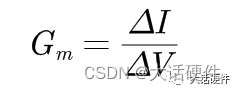
因此,跨导型的传递函数,不存在虚短和虚断,同相端的电压和反相端的电压都会参与到运算中,在该拓扑中下面的电阻必须参与传递函数。相对来说也比较好理解。
3.总结:
OPA和OTA型的拓扑结构在开关电源环路补偿中都在使用,在推导传递函数时,需要注意下分压电阻,器件的特性差异决定了下分压电阻是否需要参与到环路的传递函数中。理解器件的本质是分析两种拓扑差异的理论支撑。
相关文章:
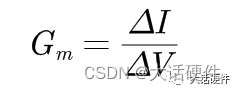
开关电源环路稳定性分析(10)——OPA和OTA型补偿器传递函数
大家好,这里是大话硬件。 在前面9讲的内容中将开关电源环路分析进行了梳理,我相信很多人即使都看完了,应该还是不会设计,而且还存在几个疑问。比如我随便举几个: 开关电源的带宽怎么设定?开关电源精度和什…...
)
2.11知识点整理(关于pycharm,python,pytorch,conda)
pycharm 设置anaconda环境: File -> Settings->选择左侧的project xxx再选择打开Project Interpreter页->选择add添加解释器->添加Anaconda中Python解释器(Anaconda安装目录下的python.exe) (选择existing environment ÿ…...
Linux服务器开发-2. Linux多进程开发
文章目录1. 进程概述1.1 程序概览1.2 进程概念1.3 单道、多道程序设计1.4 时间片1.5 并行与并发1.6 进程控制块(PCB)2. 进程的状态转换2.1 进程的状态2.2 进程相关命令查看进程实时显示进程动态杀死进程进程号和相关函数3. 进程的创建-fork函数3.1 进程创…...

Excel中缺失数据值的自动填充
目录简单方法示例1:数据满足线性趋势示例2:数据满足增长(指数)趋势参考实验做完处理数据,发现有一组数据因为设备中途出现问题缺失了,之前做过的数据也找不到,为了不影响后续处理,这里使用Excel插入缺失值。…...
路由器刷固件
前言 我希望可以远程访问我的电脑。但,我不希望电脑总是处于运行状态,因为那样比较费电。所以需要一个方案,能将睡眠/关机中的电脑唤醒。 方案一:选用智能插座,远程给电脑上电。电脑设置上电自启。但,这存…...

leetcode: Two Sum II - Input Array is Sorted
leetcode: Two Sum II - Input Array is Sorted1. 题目2. 解答3. 总结1. 题目 Given a 1-indexed array of integers numbers that is already sorted in non-decreasing order, find two numbers such that they add up to a specific target number. Let these two number…...
STL——list
一、list介绍及使用 1. list文档介绍 (1)list是可以在常数范围内,在任意位置进行插入、删除的序列式容器,并且该容器可以前后双向迭代。 (2)list的底层是带头结点的双向循环链表,其中每个元素…...
实战打靶集锦-004-My-Cmsms
**写在前面:**记录一次艰难曲折的打靶经历。 目录1. 主机发现2. 端口扫描3. 服务枚举4. 服务探查4.1 WEB服务探查4.1.1 浏览器访问4.1.2 目录枚举4.1.3 控制台探查4.1.4 其他目录探查4.2 阶段小结5. 公共EXP搜索5.1 CMS搜索5.2 Apache搜索5.3 PHP搜索5.4 MySQL搜索5…...
)
c++代码实现我的世界(14)
c代码实现我的世界14|生成地貌兼工作台1前言的前言~前言生成地貌函数结构体struct dimao根据比例生成地貌工作台函数准备的东西写在最后前言的前言~ 实在对不起大家,有挺长时间没更新了。 前言 今天我们将写生成地形的函数与工作台前传的代码; 注&…...

RMQ--区间最值问题(在更)
RMQ(Range Minimum/Maximum Query)RMQ解决的问题ST算法 O(nlogn)线段树例题数列区间最大值最敏捷的机器人天才的记忆Frequent values总结(ST和线段树对比)RMQ解决的问题 RMQ是一个解决多个区间最值查询的算法,即区间最值查询&…...
一篇文章搞懂Cookie
目录 1 什么是Cookie 2 创建Cookie 3 浏览器查看Cookie 3.1 浏览器查看Cookie的第一种方式 3.2 浏览器查看Cookie的第二种方式 4 获取Cookie 5 修改Cookie 6 Cookie编码与解码 6.1 创建带中文Cookie 6.2 读取带中文Cookie 6.3 获取中文Cookie请求效果 6.4 解决创建和…...
:播放内核)
深入解读.NET MAUI音乐播放器项目(二):播放内核
播放控制服务 IMusicControlService: 播放控制类,用于当前平台播放器对象的操作,对当前所播放曲目的暂停/播放,下一首/上一首,快进快退(寻迹),随机、单曲模式等功能的控制。 播放控制类包含一…...
4.SpringWeb
一、创建项目LomBok:辅助开发工具,减少代码编写Spring Web:带上Spring MVC,可以做Web开发了Thymleaf: Web开发末班引擎(不常用)创建好,如下:static/ 放置静态资源的根目录templates/ 放置模板文件的根目录 二、资源配置…...

C++中的枚举与位域
枚举在传统 C中,枚举类型并非类型安全,枚举类型会被视作整数,则会让两种完全不同的枚举类型可以进行直接的比较(虽然编译器给出了检查,但并非所有),甚至同一个命名空间中的不同枚举类型的枚举值…...

第19章 MongoDB Limit与Skip方法教程
第19章 MongoDB Limit与Skip方法教程 MongoDB Limit() 方法 如果仁兄需要在MongoDB中读取指定数量的数据记录,可以使用MongoDB的Limit方法,limit()方法接受一个数字参数,该参数指定从MongoDB中读取的记录条数。 语法 limit()方法基本语法请…...

进程间通信——消息队列
多线程 进程间通信——消息队列 消息队列——发送 测试代码 #include <sys/types.h> #include <sys/msg.h> #include <sys/ipc.h>#include <stdlib.h> #include <stdio.h> #include <string.h>#define MAX_BUF_SIZE 255struct msgtype {…...

OpenMMLab 实战营打卡 - 第 7 课
OpenMMLab MMSegmentation内容概要MMSegmentation统一超参MMSegmentation 的项目结构分割模型的模块化设计分割模型的配置文件主干网络的配置ResNet v1c主解码头的配置辅助解码头的配置数据集配置数据处理流水线常用训练策略参考资料内容概要 • MMSegmentation 项目概述 • M…...
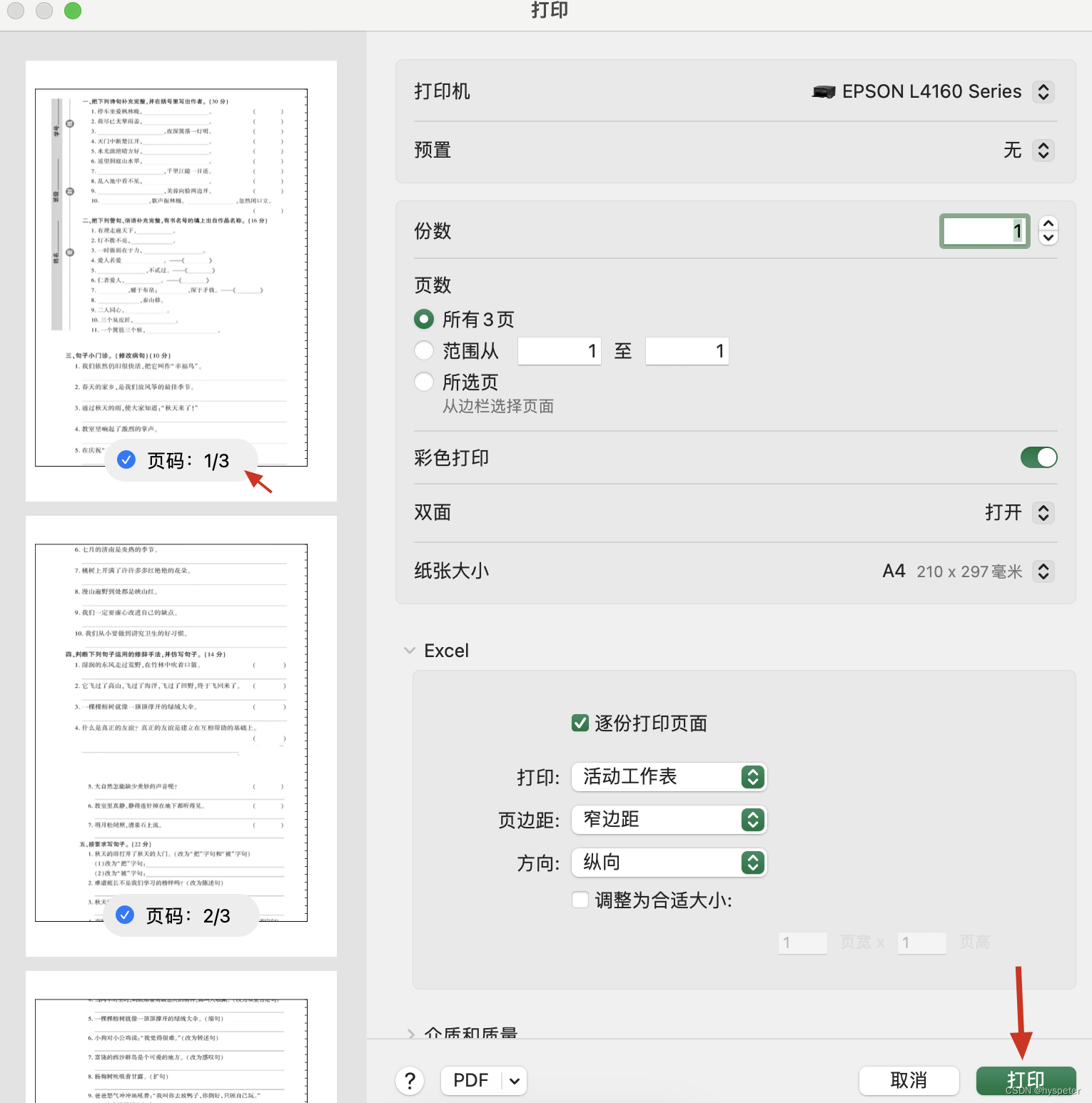
MAC Boook打印长图
有时老师给留的作业是一张长图,直接打印或者通过把图放入word打印都不能实现把长页分成多页进行打印。通过网上找到思路可以通过EXCEL实现将长图分成多页打印。 测试版本 macos:ventura 13.1 office 365 注:同样适用windows版本的excel 第…...
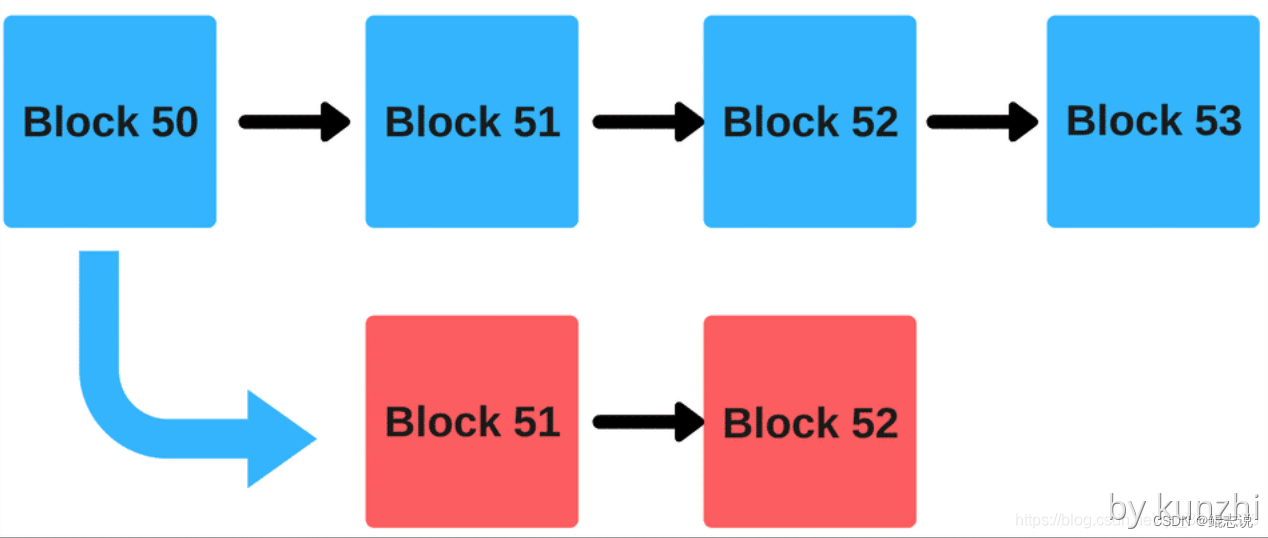
web3:区块链共识机制系列-POS(Proof of Stake)股权证明算法
web3相关学习一并收录至该博客:web3学习博客目录大全 前情衔接:web3:区块链常见的几大共识机制及优缺点 目录前言算法公式与原理算法公式运作原理以Peer Coin为例缺陷优点缺点特点分类发展历程casper协议1.什么是无成本利益关系问题2.引入casper协议解决…...
系统调用流程解析)
Linux fork()系统调用流程解析
1. fork()函数介绍(百度百科) fork系统调用用于创建一个新进程,称为子进程,它与进程(称为系统调用fork的进程)同时运行,此进程称为父进程。创建新的子进程后,两个进程将执行fork&…...

国防科技大学计算机基础课程笔记02信息编码
1.机内码和国标码 国标码就是我们非常熟悉的这个GB2312,但是因为都是16进制,因此这个了16进制的数据既可以翻译成为这个机器码,也可以翻译成为这个国标码,所以这个时候很容易会出现这个歧义的情况; 因此,我们的这个国…...

SkyWalking 10.2.0 SWCK 配置过程
SkyWalking 10.2.0 & SWCK 配置过程 skywalking oap-server & ui 使用Docker安装在K8S集群以外,K8S集群中的微服务使用initContainer按命名空间将skywalking-java-agent注入到业务容器中。 SWCK有整套的解决方案,全安装在K8S群集中。 具体可参…...

Java 8 Stream API 入门到实践详解
一、告别 for 循环! 传统痛点: Java 8 之前,集合操作离不开冗长的 for 循环和匿名类。例如,过滤列表中的偶数: List<Integer> list Arrays.asList(1, 2, 3, 4, 5); List<Integer> evens new ArrayList…...

【网络安全产品大调研系列】2. 体验漏洞扫描
前言 2023 年漏洞扫描服务市场规模预计为 3.06(十亿美元)。漏洞扫描服务市场行业预计将从 2024 年的 3.48(十亿美元)增长到 2032 年的 9.54(十亿美元)。预测期内漏洞扫描服务市场 CAGR(增长率&…...

聊聊 Pulsar:Producer 源码解析
一、前言 Apache Pulsar 是一个企业级的开源分布式消息传递平台,以其高性能、可扩展性和存储计算分离架构在消息队列和流处理领域独树一帜。在 Pulsar 的核心架构中,Producer(生产者) 是连接客户端应用与消息队列的第一步。生产者…...

Golang dig框架与GraphQL的完美结合
将 Go 的 Dig 依赖注入框架与 GraphQL 结合使用,可以显著提升应用程序的可维护性、可测试性以及灵活性。 Dig 是一个强大的依赖注入容器,能够帮助开发者更好地管理复杂的依赖关系,而 GraphQL 则是一种用于 API 的查询语言,能够提…...

2021-03-15 iview一些问题
1.iview 在使用tree组件时,发现没有set类的方法,只有get,那么要改变tree值,只能遍历treeData,递归修改treeData的checked,发现无法更改,原因在于check模式下,子元素的勾选状态跟父节…...

学习STC51单片机31(芯片为STC89C52RCRC)OLED显示屏1
每日一言 生活的美好,总是藏在那些你咬牙坚持的日子里。 硬件:OLED 以后要用到OLED的时候找到这个文件 OLED的设备地址 SSD1306"SSD" 是品牌缩写,"1306" 是产品编号。 驱动 OLED 屏幕的 IIC 总线数据传输格式 示意图 …...

CRMEB 框架中 PHP 上传扩展开发:涵盖本地上传及阿里云 OSS、腾讯云 COS、七牛云
目前已有本地上传、阿里云OSS上传、腾讯云COS上传、七牛云上传扩展 扩展入口文件 文件目录 crmeb\services\upload\Upload.php namespace crmeb\services\upload;use crmeb\basic\BaseManager; use think\facade\Config;/*** Class Upload* package crmeb\services\upload* …...

项目部署到Linux上时遇到的错误(Redis,MySQL,无法正确连接,地址占用问题)
Redis无法正确连接 在运行jar包时出现了这样的错误 查询得知问题核心在于Redis连接失败,具体原因是客户端发送了密码认证请求,但Redis服务器未设置密码 1.为Redis设置密码(匹配客户端配置) 步骤: 1).修…...
