DP:数位DP
数位DP的大致思想:枚举每一位能选取的合法值。
1. LC 2376 统计特殊整数
说是DP,但实际上状态转移方程挺难写的,毕竟是枚举+集合论,这里就不贴状态转移方程了。总体的写法其实是搜索+记忆化。之所以称之为DP,是因为:
- 对于第i位,
- 如果[0,i-1]位全部都选的能选的最大值,那么第i位最多也就只能选到最大值(注意第0位肯定是受限制的)
- 否则,第i位能随便选
- 如果前面[0,i-1]位都是0(前导零),这一位就可以随便选了
有这两大状态转移的规则,所以还是被称之为DP。细节写在代码里了
import java.util.Arrays;class Solution {char[] s;int[][] memo;public int countSpecialNumbers(int n) {s = Integer.toString(n).toCharArray();// 记搜// memo[i][mask]代表[0,i-1]位选掉了mask中各个索引位置代表的数的情况下后面有多少个特殊整数memo = new int[s.length][1<<10];for (int i = 0; i < memo.length; i++) {Arrays.fill(memo[i],-1); // -1 代表没有计算过}// 一开始第一位当然要受限制,不过也可以是前导零,所以 (true,false)return f(0,0,true,false);}/*** 记搜计算在确定[0,i-1]位后剩下的有种特殊整数的情况* @param i 第i位* @param mask 已经选择了mask集合中的数* @param isLimit 当前位上限是否有限制,有的话是 int(s[i]),没有的话是9* @param isNum 当前位是否跳过,即前导零* @return 确定[0,i-1]位后剩下的有种特殊整数的情况*/private int f(int i,int mask,boolean isLimit,boolean isNum){if(i==s.length){return isNum ?1:0; // 防止从头到尾的前导零,这种情况根本不是个数字,当然不能算}/*这个!isLimit条件非常重要,举个例子,n=420假设现在前两位选了 4,2,那么mask = {4,2},第三位就只能选0但如果前两位选了2,4,mask={4,2},第三位可以随便选(除了2,4)在第一种情况下能选1种,第二种情况下能选8种(10-2),差了7种情况而之后的循环枚举会考虑所有顶着最大上限选的情况,所以如果当前这个数位受到最大上限的限制的话,后面的for循环会统计这个情况的而不是把非受限制的情况的记忆化搜索结果返回,在这个例子里dp[2][{2,4}] = 8 而不是1但isNum不是必须判断的,因为如果前面都受限制,后面一位也一定受限制,可前面都是前导零,不代表后面也得是前导零况且,[0,i-1]位全是前导零的情况,顶多出现一次,后面再怎么递归都不可能有的*/if(!isLimit && memo[i][mask]!=-1){return memo[i][mask];}int res = 0;if(!isNum){// 含前导零,跳过res = f(i+1,mask,false,false);}// 当前位置是否受限制int upper = isLimit?s[i]-'0':9;// 枚举可以填充的数,这里要检查是否之前使用了前导零,使用了的话要去掉(之前if(!isNum)加过了),没有用的话可以从0开始for (int j = isNum?0:1; j <= upper; j++) {// 特殊整数要求各数位都不一样,所以检查mask中之前用过没// mask就是个位图,比如 binary(mask) = 0101010111 从右往左看,用集合论表示就是 {8,6,4,2,1,0} 这些数字已经被用过了if((mask>>j&1)==0){// 用掉j就是把mask的第j位设置为0 mask|(1<<j)// 那么下一个数位是否受限制呢?如果当前数位受限制并且当前数位选取了上限,那么下一位是受限制的,否则不受限制// 例如,n = 123 i=1,假设当前数位不受上限,那么也就是说这个数<=99,下一位当然也不受限制// 但若受限制,则代表前面i=0的时候选择了上限1,i=1选择最多是2,下一位自然受限制,最大是3// 最后,既然这一位枚举了一位有意义的数字,后续的枚举自然也是有意义的, isNum 为 trueres += f(i+1,mask|(1<<j),isLimit && j==upper,true);}}// 记忆化if(!isLimit){memo[i][mask] = res;}return res;}
}
2. LC 233 数字1的个数
这题是我学了板子后做的第一题,真的汗流浃背。想想做做调调,卡了1h才出来。
首先这个跟上面一题的区别是,对于枚举的数字没有限制。不仅没有重复性的限制,而且还没有前导零的限制(前导零的数不会被判无效,因为这道题只看1的数量)
这样就简便了不少。我们只需要看是否被上限限制即可。这个是否受限还是和以前一样,只有前面的都受限,本次才会受限,否则不会。
令f(i,isLimit)表示第[i,n-1]位在Limit的限制下能产生的1的数量。那么本轮的上限可以由isLimit计算得出:
-
如果upper<1,也就是upper=0的情况,本轮不可能选1
-
如果upper==1,本轮选择1会产生 int(suffix(n,i+1))+1 个1。其中suffix(n,i+1)代表n的[i+1,n-1]位的值,例如 n = 2132 , i=1 那么suffix(2232,2) = 32。
这是比较显然的,拿上面那个例子来说,如果本轮选择1,后续会有2100到2132这些数的第i=1位是1,所以就是32-00+1=33个
-
如果upper>1,本轮选择1会产生 pow(10,n-i-1)个1。例如n=2232,i=1,那么如果本轮选择1,就会有2100到2199的第i=1位是1,也就是pow(4-1-1)=100个
以上考虑的是本轮(第i位)产生的1的数量。后面[i+1,n-1]产生的还没算:
两种情况讨论。上限是upper,说明本轮有upper种选择,其中可能有一种是顶格选的(isLimit情况),有upper种是非顶格选的。依次累加到res即可。这里对于前者,根据当前的isLimit来(如果当前顶格了后面也得顶格,当前不顶格后面也不顶格),根据后者,isLimit = false
最后,记搜的时候要记得排除顶格选的情况。因为这种情况已经被统计过了。
import java.util.Arrays;class Solution {char[] s;int[] memo;public int countDigitOne(int n) {s = Integer.toString(n).toCharArray();memo = new int[s.length];Arrays.fill(memo,-1);return f(0,true);}/*** 记搜计算[0,i-1]位选择完毕后,后面的位置总共能出现多少个1* @param i 第i位* @param isLimit 受到最大上限限制与否* @return [0,i-1]位选择完毕后,后面的位置总共能出现多少个1*/private int f(int i,boolean isLimit){if(i==s.length){return 0;}/*例如:n = 1230 ,现在 i=[0,1,2] = {1,2,3},那么后面一个1都不可能有但如果i=[0,1,2] = {1,2,2},后面是可以有一个1的memo记录的是后者*/if(!isLimit && memo[i]!=-1){return memo[i];}int res = 0;int upper = isLimit?s[i]-'0':9;// 如果这一轮选1if(upper==1){res += suffix(i+1)+1;}else if(upper>1){res += (int) Math.pow(10,s.length-i-1);}// 本来可以选 upper+1个数(这一轮)// 如果之前全部都顶格选了,那么将是upper个可以后续不用顶格选的,和一个必须顶格选的res += upper*f(i+1,false) + f(i+1,isLimit);if(!isLimit){memo[i] = res;}return res;}private int suffix(int start){StringBuilder sb = new StringBuilder();for(int i=start;i<s.length;i++){sb.append(s[i]);}return sb.isEmpty()?0:Integer.parseInt(sb.toString());}
}
3. LC 2719 统计整数数目
这道题我思路有的,但就是有点歪,所以虽然A了但是时间上表现不好
首先我的记搜是包含4个状态的:定义 f (i,isLower,isUpper,acc)表示在[0,i-1]位均已枚举,且数位和为acc,且是(否)受下限与上限的制约的情况下,后续能够产生的符合条件的数。
那么上限和下限分别怎么算?我通过补齐较小的num1的前导零,使其与num2在数位长度上等长。这样下限由num1(补齐前导零后)决定,上限由num2决定。
在深搜时记忆化在不受上下限制约的情况下,在枚举到第i位且已有数位累计和acc的情况下,后续能有多少个符合条件的数。
之后根据是否受上下限制约枚举数位即可。这里注意枚举时可以及时地判断是否已经爆掉数位和上界了,而下界可以留到最终递归基的是否判断。
最后,我现在是觉得,模运算这个东西,有很强的性质(加法乘法的性质都特别强),如果担心答案爆了怎么办,就在能取模的地方全部取模就行。
import java.util.Arrays;class Solution {static long mod = (long)1e9+7;char[] s1;char[] s2;long[][] memo;int min;int max;public int count(String num1, String num2, int min_sum, int max_sum) {min = min_sum;max = max_sum;s1 = supplyLeadingZero(num1,num2).toCharArray();s2 = num2.toCharArray();// memo[i][acc]代表在不受限制的情况下 到了第i位已经有acc的数位和,第[i+1,n-1]位最多能有多少个符合条件的数memo = new long[s2.length][22*9+1];for (int i = 0; i < memo.length; i++) {Arrays.fill(memo[i],-1L);}return (int) (f(0,true,true,0) % mod);}private String supplyLeadingZero(String num1,String num2){StringBuilder num1Builder = new StringBuilder(num1);while(num1Builder.length()<num2.length()){num1Builder.insert(0, "0");}num1 = num1Builder.toString();return num1;}private long f(int i,boolean isLower,boolean isUpper,int acc){if(i==s2.length){return acc>=min?1L:0L;}if(!isLower && !isUpper && memo[i][acc]!=-1){return memo[i][acc];}int lb = isLower?s1[i]-'0':0;int ub = isUpper?s2[i]-'0':9;long res = 0L;for(int j=lb;j<=ub;j++){if(max>=acc+j){res = (res%mod + f(i+1,isLower && j==lb, isUpper && j==ub, acc+j)%mod) % mod;}}if(!isLower && !isUpper){memo[i][acc] = res;}return res;}
}
还有一种更常见的思路是,先统计一遍≤num1的情况,再统计一遍≤num2的情况,然后后者减前者就是(num1,num2]的情况。又因为题目是闭区间,所以单独判一下num1符合条件与否即可。这种思路跑得比我的代码快,这里摘录一份:
class Solution {private static final int MOD = 1_000_000_007;public int count(String num1, String num2, int minSum, int maxSum) {int ans = calc(num2, minSum, maxSum) - calc(num1, minSum, maxSum) + MOD; // 避免负数int sum = 0;for (char c : num1.toCharArray()) {sum += c - '0';}if (minSum <= sum && sum <= maxSum) {ans++; // num1 是合法的,补回来}return ans % MOD;}private int calc(String s, int minSum, int maxSum) {int n = s.length();int[][] memo = new int[n][Math.min(9 * n, maxSum) + 1];for (int[] row : memo) {Arrays.fill(row, -1);}return dfs(0, 0, true, s.toCharArray(), minSum, maxSum, memo);}private int dfs(int i, int sum, boolean isLimit, char[] s, int minSum, int maxSum, int[][] memo) {if (sum > maxSum) { // 非法return 0;}if (i == s.length) {return sum >= minSum ? 1 : 0;}if (!isLimit && memo[i][sum] != -1) {return memo[i][sum];}int up = isLimit ? s[i] - '0' : 9;int res = 0;for (int d = 0; d <= up; d++) { // 枚举当前数位填 dres = (res + dfs(i + 1, sum + d, isLimit && (d == up), s, minSum, maxSum, memo)) % MOD;}if (!isLimit) {memo[i][sum] = res;}return res;}
}
相关文章:

DP:数位DP
数位DP的大致思想:枚举每一位能选取的合法值。 1. LC 2376 统计特殊整数 说是DP,但实际上状态转移方程挺难写的,毕竟是枚举集合论,这里就不贴状态转移方程了。总体的写法其实是搜索记忆化。之所以称之为DP,是因为&am…...

js逆向第21例:猿人学第20题新年挑战
文章目录 一、前言二、定位加密参数1、定位wasm加密2、反编译wasm3、定位sign加密三、代码实现四、参考文献一、前言 新春福利:抓取这5页的数字,计算加和并提交结果 二、定位加密参数 通过get请求地址可以看到需要搞定参数有page、sign、t如下图: 进入堆栈不难发现这样一…...

贪心+蓝桥杯
原题路径 题目思路 : 思路很简单,肯定是贪心做法,要使总代价最小,需用那些出现次数比avg多的数来替换那些没有出现或者是出现次数少于avg的数, 所以我们存当前数每次出现的代价是多少 ,枚举每一个 0 - 9 之间的数 ,如果当前数出现…...

第二篇:新建node项目并运行
🎬 江城开朗的豌豆:个人主页 🔥 个人专栏 :《 VUE 》 《 javaScript 》 📝 个人网站 :《 江城开朗的豌豆🫛 》 ⛺️ 生活的理想,就是为了理想的生活 ! 安装 Node.js:首先,确保你的…...

阳光保险选择OceanBase稳定运行超700天
阳光保险集团成立于 2005 年 7 月,旗下拥有财产保险、人寿保险、信用保证保险、资产管理等多家专业子公司,是全球市场化企业中成长最快的集团公司之一,目前位列中国保险行业前八。随着数字化升级趋势的不断加速,很多企业产生将软硬…...

最强大脑闪电心算草稿1
#include<bits/stdc.h> #include<windows.h> using namespace std; int main() {double speed,n,op,sum0;int ans;srand(time(NULL));cout<<"请输入加(1)/减(2)/加减混合(3):";cin>>op;cout<<"请输入题目数量:";cin>>…...

融优学堂-艺术史
导论4 1.【单选题】根据导论的讲解,下列表述正确的是()。(1)艺术品是因人的活动而被创造出来的人工制品。(2)许多物品被制造出来时,最初的目的是满足某种实用的用途,而不…...
༺༽༾ཊ—设计-七个-07-原则-模式—ཏ༿༼༻
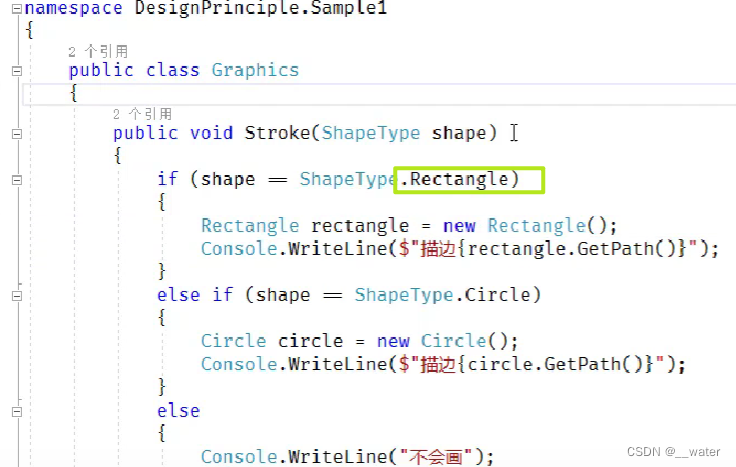
第七原则:迪米特职责 类与类之间的耦合度尽可能低 换言之,我们可以理解成———只与直接朋友说话,不跟陌生人说话 直接朋友: 通过方法传参传进来的朋友, 类自己的字段, 构造函数进来的也是直接朋友&…...

一篇文章带你搞懂---全排序
顾得泉:个人主页 个人专栏:《Linux操作系统》 《C/C》 《LeedCode刷题》 键盘敲烂,年薪百万! 全排序(Permutation)是指将一组元素按照一定的顺序进行排列的过程。在计算机科学中,全排序是一…...

提升问题检索的能力
事实上,在信息极度丰富的时代,信息检索和筛选能力格外重要。一些搜索引擎的出现已极大地方便了我们日常的信息检索,此处需要注意的是我们不能仅仅局限于常见的搜索引擎,也需要关注和积累一些专业平台或是具有集成功能的引擎&#…...

软件测试|SQLAlchemy query() 方法查询数据
简介 上一篇文章我们介绍了SQLAlchemy 的安装和基础使用,本文我们来详细介绍一下如何使用SQLAlchemy的query()方法来高效的查询我们的数据。 创建模型 我们可以先创建一个可供我们查询的模型,也可以复用上一篇文章中我们创建的模型,代码如…...
FlinkCDC的分析和应用代码
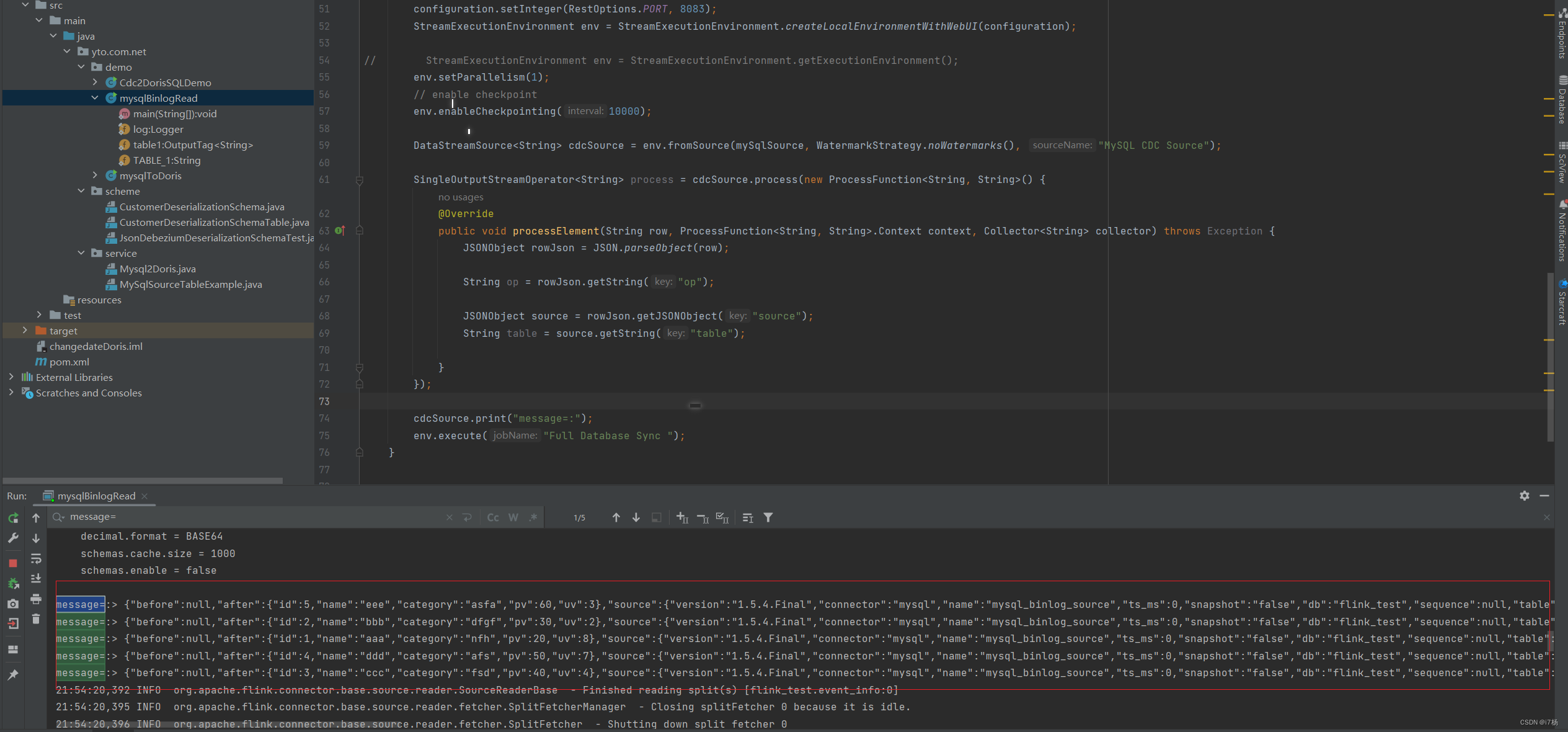
前言:原本想讲如何基于Flink实现定制化计算引擎的开发,并以FlinkCDC为例介绍;发现这两个在表达上不知以谁为主,所以先分析FlinkCDC的应用场景和技术实现原理,下一篇再去分析Flink能在哪些方面,做定制化计算…...
序章 搭建环境篇—准备战士的剑和盾
第一步:安装node.js Node.js 内置了npm,只要安装了node.js,就可以直接使用 npm,官网地址: Download | Node.js 在这里不建议安装最新版本的node.js,可以选跟我一样的版本,node版本v16.13.2 链…...

【C++】vector的使用及模拟实现
目录 一、vector的介绍及使用1.1 介绍vector1.2 vector的使用1.2.1 构造1.2.2 遍历访问1.2.3 容量空间1.2.4 增删查改 二、vector的模拟实现2.1 成员变量2.2 迭代器相关函数2.3 构造-析构-赋值重载2.3.1 无参构造2.3.2 有参构造12.3.3 有参构造22.3.4 拷贝构造2.3.5 赋值重载2.…...

【数据库】sql优化有哪些?从query层面和数据库层面分析
目录 归纳sql本身的优化数据库层面的优化 归纳 这类型问题可以称为:Query Optimization,从清华AI4DB的paper list中,该类问题大致可以分为: Query RewriterCardinality EstimationCost EstimationPlan Optimization 从中文的角…...

nginx基本优化
安装nginx隐藏版本号 查看百度web服务器 [rootcjq11 ~]# curl -I http://www.baidu.com 隐藏nginx服务器版本号 [rootcjq11 ~]# cd /usr/local/src/nginx-1.22.0/ [rootcjq11 nginx-1.22.0]# vim src/core/nginx.h第13、14行修改版本号和服务器名称 [rootcjq11 nginx-1.2…...

软件测试|使用selenium处理单选框和多选框
简介 我们在web自动化测试工作中,经常会遇到对单选框(Radio Buttons)或者多选框(Checkboxes)进行操作的场景,单选框和多选框主要是用于我们做出选择或提交数据。本文将主要介绍selenium对于单选框和多选框…...
的有效值列表)
openssl3.2 - EVP_CIPHER_fetch算法名称字符串(参数2)的有效值列表
文章目录 openssl3.2 - EVP_CIPHER_fetch算法名称字符串(参数2)的有效值列表概述如何找到算法名称字符串列表?openssl-3.2.0\providers\implementations\include\prov\names.h备注END openssl3.2 - EVP_CIPHER_fetch算法名称字符串(参数2)的有效值列表 概述 进行加解密时, 先…...

vue3中的hook公共函数封装及运用
vue3 中的 hooks 就是函数的一种写法,就是将文件的一些单独功能的js代码进行抽离出来,放到单独的js文件中,或者说是一些可以复用的公共方法/功能 使用Vue3的组合API封装的可复用的功能函数自定义hook的作用类似于vue2中的mixin技术自定义Hook…...

广州市工信局、天河区商务金融局及广州专精特新促进会走访思迈特
2024年1月11日下午,广州市工信局、天河区商务金融局及广州专精特新促进会相关负责人莅临广州思迈特软件总部调研指导,思迈特软件总裁兼COO姚诗成代表公司热情接待,并陪同调研。 调研组实地参观了思迈特软件,深入了解了思迈特发展历…...

PPT|230页| 制造集团企业供应链端到端的数字化解决方案:从需求到结算的全链路业务闭环构建
制造业采购供应链管理是企业运营的核心环节,供应链协同管理在供应链上下游企业之间建立紧密的合作关系,通过信息共享、资源整合、业务协同等方式,实现供应链的全面管理和优化,提高供应链的效率和透明度,降低供应链的成…...

【SpringBoot】100、SpringBoot中使用自定义注解+AOP实现参数自动解密
在实际项目中,用户注册、登录、修改密码等操作,都涉及到参数传输安全问题。所以我们需要在前端对账户、密码等敏感信息加密传输,在后端接收到数据后能自动解密。 1、引入依赖 <dependency><groupId>org.springframework.boot</groupId><artifactId...

vscode(仍待补充)
写于2025 6.9 主包将加入vscode这个更权威的圈子 vscode的基本使用 侧边栏 vscode还能连接ssh? debug时使用的launch文件 1.task.json {"tasks": [{"type": "cppbuild","label": "C/C: gcc.exe 生成活动文件"…...

解决Ubuntu22.04 VMware失败的问题 ubuntu入门之二十八
现象1 打开VMware失败 Ubuntu升级之后打开VMware上报需要安装vmmon和vmnet,点击确认后如下提示 最终上报fail 解决方法 内核升级导致,需要在新内核下重新下载编译安装 查看版本 $ vmware -v VMware Workstation 17.5.1 build-23298084$ lsb_release…...

Unsafe Fileupload篇补充-木马的详细教程与木马分享(中国蚁剑方式)
在之前的皮卡丘靶场第九期Unsafe Fileupload篇中我们学习了木马的原理并且学了一个简单的木马文件 本期内容是为了更好的为大家解释木马(服务器方面的)的原理,连接,以及各种木马及连接工具的分享 文件木马:https://w…...

Yolov8 目标检测蒸馏学习记录
yolov8系列模型蒸馏基本流程,代码下载:这里本人提交了一个demo:djdll/Yolov8_Distillation: Yolov8轻量化_蒸馏代码实现 在轻量化模型设计中,**知识蒸馏(Knowledge Distillation)**被广泛应用,作为提升模型…...

代码随想录刷题day30
1、零钱兑换II 给你一个整数数组 coins 表示不同面额的硬币,另给一个整数 amount 表示总金额。 请你计算并返回可以凑成总金额的硬币组合数。如果任何硬币组合都无法凑出总金额,返回 0 。 假设每一种面额的硬币有无限个。 题目数据保证结果符合 32 位带…...

群晖NAS如何在虚拟机创建飞牛NAS
套件中心下载安装Virtual Machine Manager 创建虚拟机 配置虚拟机 飞牛官网下载 https://iso.liveupdate.fnnas.com/x86_64/trim/fnos-0.9.2-863.iso 群晖NAS如何在虚拟机创建飞牛NAS - 个人信息分享...

windows系统MySQL安装文档
概览:本文讨论了MySQL的安装、使用过程中涉及的解压、配置、初始化、注册服务、启动、修改密码、登录、退出以及卸载等相关内容,为学习者提供全面的操作指导。关键要点包括: 解压 :下载完成后解压压缩包,得到MySQL 8.…...

华为OD机试-最短木板长度-二分法(A卷,100分)
此题是一个最大化最小值的典型例题, 因为搜索范围是有界的,上界最大木板长度补充的全部木料长度,下界最小木板长度; 即left0,right10^6; 我们可以设置一个候选值x(mid),将木板的长度全部都补充到x,如果成功…...
