C语言经典算法之堆排序算法
目录
前言
建议
简介
A.建堆:
B.排序
一、代码实现
二、时空复杂度
A.时间复杂度
B.空间复杂度
三、稳定性
四、现实中的应用
前言
建议
1.学习算法最重要的是理解算法的每一步,而不是记住算法。
2.建议读者学习算法的时候,自己手动一步一步地运行算法。
tips:文中的对数均以2为底数
简介
堆排序是一种基于堆数据结构的排序算法。它分为两个主要步骤:建堆和排序。
A.建堆:
建堆的过程是将一个无序的数组构建成一个堆,通常采用最大堆(Max Heap)的形式。最大堆是一种特殊的二叉树,其中每个节点的值都大于或等于其子节点的值。下面是建堆的简单步骤:
1.从最后一个非叶子节点开始: 最后一个非叶子节点的索引可以通过 (n/2 - 1) 计算,其中 n 是数组的长度。非叶子节点是指有子节点的节点。
2.进行堆调整(Heapify): 对于每个非叶子节点,进行堆调整,将当前节点与其子节点比较,确保当前节点是最大的。如果子节点的值较大,则交换节点值,然后递归地调整子树。
3.逐层向上重复: 重复步骤2,逐层向上处理非叶子节点,直到根节点。这样就确保了整个数组构成了一个最大堆。
B.排序
排序的过程是将一个无序的数据集合按照一定规则重新排列成有序的序列。以下是一般排序算法的简单过程:
1.比较元素: 排序算法的第一步是通过比较元素来确定它们的相对顺序。比较可以根据不同的规则进行,例如升序或降序。
2.交换元素: 根据比较的结果,可能需要交换元素的位置以达到正确的顺序。这是排序算法中一个关键的步骤。
3.重复步骤1和2: 排序算法会持续比较和交换元素,直到整个数据集合中的元素都按照规则有序排列。
一、代码实现
#include <stdio.h>// 交换数组中两个元素的值
void swap(int *a, int *b) {int temp = *a;*a = *b;*b = temp;
}// 调整堆,保持最大堆性质
void maxHeapify(int arr[], int n, int i) {int largest = i; // 初始化最大值的索引为根节点int left = 2 * i + 1; // 左子节点的索引int right = 2 * i + 2; // 右子节点的索引// 如果左子节点比根节点大,则更新最大值的索引if (left < n && arr[left] > arr[largest]) {largest = left;}// 如果右子节点比当前最大值大,则更新最大值的索引if (right < n && arr[right] > arr[largest]) {largest = right;}// 如果最大值的索引不是根节点,交换它们的值并递归调整子树if (largest != i) {swap(&arr[i], &arr[largest]);maxHeapify(arr, n, largest);}
}// 建立最大堆
void buildMaxHeap(int arr[], int n) {// 从最后一个非叶子节点开始,逐个调整子树使其满足最大堆性质for (int i = n / 2 - 1; i >= 0; i--) {maxHeapify(arr, n, i);}
}// 堆排序主函数
void heapSort(int arr[], int n) {// 建立最大堆buildMaxHeap(arr, n);// 从最后一个元素开始,逐个将当前最大元素交换到数组末尾for (int i = n - 1; i > 0; i--) {swap(&arr[0], &arr[i]); // 将当前最大元素移动到数组末尾maxHeapify(arr, i, 0); // 调整堆,保持最大堆性质}
}// 打印数组
void printArray(int arr[], int size) {for (int i = 0; i < size; i++) {printf("%d ", arr[i]);}printf("\n");
}int main() {int arr[] = {12, 11, 13, 5, 6, 7};int n = sizeof(arr) / sizeof(arr[0]);printf("原始数组: ");printArray(arr, n);heapSort(arr, n);printf("堆排序后的数组: ");printArray(arr, n);return 0;
}
这段代码首先建立一个最大堆,然后通过不断交换根节点和最后一个节点,并调整堆的方式,实现堆排序。
二、时空复杂度
A.时间复杂度
堆排序算法的时间复杂度主要由两个部分构成:建堆的时间复杂度和排序的时间复杂度。
建堆时间复杂度: 建堆的过程需要从最后一个非叶子节点开始,对每个节点进行堆调整(Heapify),使得整个数组构成一个最大堆。建堆的时间复杂度是,其中n是数组的长度。
排序时间复杂度: 在建堆完成后,堆的根节点是数组中的最大元素。将根节点与数组末尾的元素交换,然后重新调整堆,这样就把最大的元素放到了数组末尾。重复这个过程,每次交换后堆的大小减一,直到整个数组有序。由于进行n次交换和调整,排序的时间复杂度也是。
因此,堆排序的总时间复杂度是建堆和排序时间复杂度的和:。
B.空间复杂度
堆排序的空间复杂度主要包括两个方面:原地排序所需的空间和递归调用的栈空间。
原地排序: 堆排序是一种原地排序算法,它不需要额外的辅助数组来存储数据。排序过程中主要是通过在输入数组上进行元素交换,而不需要额外的存储空间。因此,原地排序的空间复杂度为 O(1)。
递归调用的栈空间: 在堆排序的建堆过程中,通常会使用递归调用或迭代方式来实现堆调整。递归调用会在调用栈中占用一定的空间,其空间复杂度与递归深度相关。最坏情况下,堆排序的递归深度为堆的高度,即,其中 n 是输入数组的长度。因此,递归调用的空间复杂度为
。
因此,原地排序和递归调用的空间开销,堆排序的总体空间复杂度为 :。这表明堆排序的空间需求相对较低,是一个空间效率较好的排序算法。
三、稳定性
在排序过程中,可能会交换相同值的元素的相对位置,导致相等元素之间的原始相对顺序被打乱。具体来说,在建堆和排序的过程中,会涉及到元素的交换操作。如果两个相等元素的顺序在排序之前是相对的,那么在排序之后,它们的相对顺序可能会发生变化。由于堆排序是通过不断交换堆顶元素和数组末尾元素,并调整堆的过程来实现的,这种交换可能破坏相同元素的相对顺序。因此,堆排序不是稳定的排序算法。
四、现实中的应用
堆排序虽然在某些方面不如一些简单的排序算法直观,但在现实中仍然有一些应用场景,其中它的优势得到充分发挥:
优先队列: 堆排序常用于实现优先队列,其中最大堆或最小堆的性质使得可以高效地找到最大或最小元素。这在任务调度、事件模拟等领域有广泛应用。
堆作为数据结构的一部分: 堆结构本身作为一种数据结构,可以被应用于图算法中的最短路径算法(如Dijkstra算法)和最小生成树算法(如Prim和Kruskal算法)等。堆排序作为堆结构的一种附带应用,用于维护和操作堆。
外部排序: 在需要对大规模数据进行排序的情况下,堆排序相对于其他算法的稳定的时间复杂度使得它成为外部排序算法的一种选择。外部排序涉及到将大量数据从外部存储(例如硬盘)加载到内存中进行排序,然后再写回外部存储。
不稳定排序的需求: 在某些情况下,不需要保持相同值元素的相对顺序,而更关注排序算法的性能,此时堆排序可以是一个合适的选择。
相关文章:
C语言经典算法之堆排序算法
目录 前言 建议 简介 A.建堆: B.排序 一、代码实现 二、时空复杂度 A.时间复杂度 B.空间复杂度 三、稳定性 四、现实中的应用 前言 建议 1.学习算法最重要的是理解算法的每一步,而不是记住算法。 2.建议读者学习算法的时候,自己…...
)
前端笔试题(一)
1.vue如何实现数据的双向绑定 利用v-model来实现双向数据绑定 通过Object.defineProperty()来劫持各个属性的setter,getter,在数据变动时发布消息给订阅者,触发相应的监听回调来渲染视图 2.使用vue渲染大量数据时,如何进行优化…...

Springboot开发的大学生寝室考勤系统刷脸进出宿舍系统技术文档
宿舍出入系统 1.2采集学生人脸信息和宿管人脸信息 前端使用navigator.mediaDevices.getUserMedia(考虑个浏览器的内核差异,此处以最新的标准API:navigator.mediaDevices.getUserMedia为例)获取用户浏览器的摄像头并开启视频,使用…...
网络共享服务
存储类型:直连式(DAS):距离最近,存储设备且直接连接到服务器上 存储区域网络(SAN):适用于大型应用或数据库系统,可以使用文件的空间, 以及管理空间…...

资本主义的市场竞争?IBM总监Jerry Chow 谈量子计算的未来
人物介绍:Jerry M.Chow博士在耶鲁大学取得物理博士学位。担任IBM量子系统总监,其研究重点是面向容错量子计算的多量子比特系统。他主要为IBM的量子系统路线图制定战略,与硬件团队领导者一起设定目标研究领域,同时也确保最佳的客…...
什么是残差矢量量化?
一、说明 基于残差矢量量化的神经音频压缩方法正在重塑现代音频编解码器的格局。在本指南中,了解 RVQ 背后的基本思想以及它如何增强神经压缩。 数据压缩在当今的数字世界中发挥着关键作用,促进信息的高效存储和传输。由于当今超过 80% 的互联网流量来自…...
复习提纲2)
计算机网络(第六版)复习提纲2
二、物理层 2.1 物理层基本概念 物理层协议常常成为物理层规程 物理层的主要任务为确定与传输媒体的接口有关的一些特性: 1.机械特性:指明接口所用接线器的尺寸等; 2.电气特性:指明接口电缆各条线上的电压范围; 3.功能…...

11k+star 开源笔记应用真香 centos部署教程
leanote binary installation on Mac and Linux (En) life edited this page on Jul 21, 2017 10 revisions Pages 26 Home How to develop leanote 如何开发leanote How to install leanote on Ubuntu? How to Upgrade Leanote Install Mongodb leanote api leanote …...
win下安装tensorflow
1首先ctrlaltdelete打开任务管理器查看GPU型号 2或者右键我的电脑然后如下方式查看显卡发现没有navida没有GPU...

SpringBoot 入门
1.SpringBoot介绍 1.1.什么是SpringBoot Spring Boot是由Pivotal团队提供的全新框架,其中“Boot”的意思就是“引导”,Spring Boot 并不是对 Spring 功能上的增强,而是提供了一种快速开发 Spring应用的方式。 1.2.Spring Boot 特点 • 嵌…...

使用WebFlux处理WebSocket连接的全生命周期案例
使用WebFlux处理WebSocket连接的全生命周期案例 简介: 在Web应用程序开发中,WebSocket是一种用于实现双向通信的协议。Spring WebFlux提供了对WebSocket的支持,使您能够轻松地处理WebSocket连接和消息。本博客将介绍如何使用WebFlux处理WebS…...
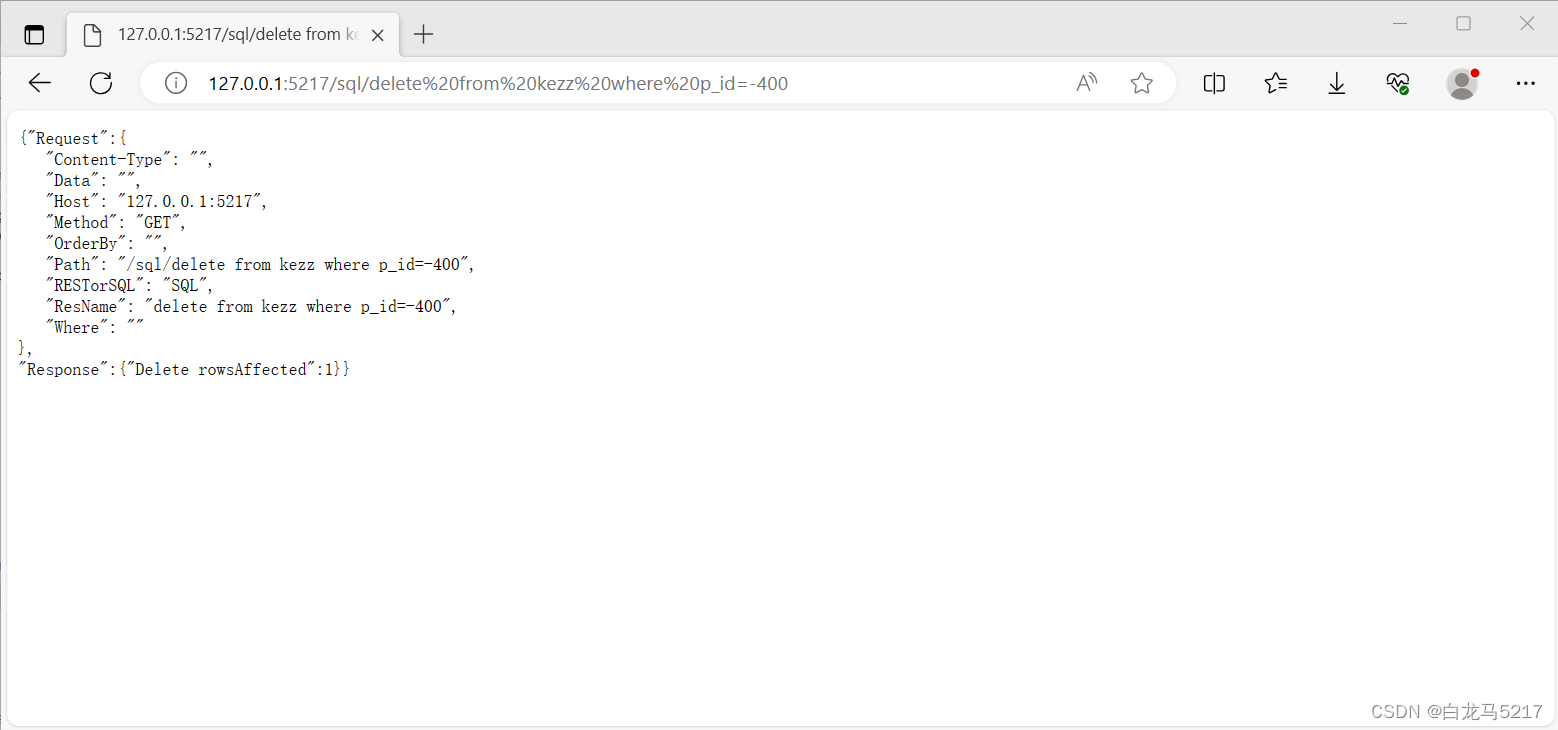
【REST2SQL】10 REST2SQL操作指南
【REST2SQL】01RDB关系型数据库REST初设计 【REST2SQL】02 GO连接Oracle数据库 【REST2SQL】03 GO读取JSON文件 【REST2SQL】04 REST2SQL第一版Oracle版实现 【REST2SQL】05 GO 操作 达梦 数据库 【REST2SQL】06 GO 跨包接口重构代码 【REST2SQL】07 GO 操作 Mysql 数据库 【RE…...

199_二叉树的右视图
描述 给定一个二叉树的 根节点 root,想象自己站在它的右侧,按照从顶部到底部的顺序,返回从右侧所能看到的节点值。 思路 对树进行深度优先搜索,在搜索过程中,我们总是先访问右子树。那么对于每一层来说,…...

第七讲_css浮动
css浮动 1. 设置浮动2. 浮动的特点3. 浮动的影响4. 解决浮动的影响4.1 解决父元素高度塌陷的问题4.2 解决对兄弟元素影响问题 1. 设置浮动 浮动是通过float属性设置,float取值范围: none:不浮动,默认值。left:向左浮…...

2024秋招,顺丰科技测试开发工程师一面
前言 今天回顾一下,一个被捞的全流程面试经历 时间线 9月21日测评 10月26日技术一面,本来是11点半开始,我正做另一个笔试呢,突然给我打电话开面 20分钟结束,一开始以为KPI,结果给过了 10月31日技术二…...
基于apache的http文件服务配置
背景: 公司的产品使用的第三方模组可以OTA,厂家提供的是window开启软件,这样就可以在本机做http下载服务器,然后使用端口映射的方式,公开到外网,这样就可以进行4G网络访问内网服务器了。但这个有个弊端&am…...

连铸工艺和模铸工艺有什么区别。
问题描述:连铸工艺和模铸工艺有什么区别。 问题解答: 连铸工艺和模铸工艺在多个方面存在显著差异: 指代不同: 模铸是成批大量生产锻件的锻造方法。连铸即为连续铸钢的锻造方法。 工艺不同: 模铸在锻压机械的作用…...

pyqt treeWidget树生成
生成treeWidget树与获取treeWidget树节点的数据 # encodingUTF-8 import sys from PyQt5.QtCore import Qt from PyQt5.QtWidgets import QApplication, QTreeWidgetItem, QLineEdit, QSpinBox, QComboBox from PyQt5.QtWidgets import QWidget from release_test import Ui_F…...

DataFunSummit:2023年云原生大数据峰会:核心内容与学习收获(附大会核心PPT下载)
随着数字化转型的深入推进,大数据技术已经成为企业获取竞争优势的关键因素之一。本次峰会汇聚了业界顶尖的大数据专家、企业领袖和技术精英,共同探讨云原生大数据领域的最新技术和趋势。本文将深入分析峰会的核心内容,并探讨参会者从中能学到…...

docker 容器添加指定网络地址
docker 容器添加指定网络地址 在搭建halo博客时,准备让 halo、mysql8.1、nginx 三个容器在同一个网段中,并指定IP。 实现docker内部容器之间网络互通。 查看容器网络信息命令 docker inspect 容器名各容器部署成功后网络效果如下: nginx …...

零门槛NAS搭建:WinNAS如何让普通电脑秒变私有云?
一、核心优势:专为Windows用户设计的极简NAS WinNAS由深圳耘想存储科技开发,是一款收费低廉但功能全面的Windows NAS工具,主打“无学习成本部署” 。与其他NAS软件相比,其优势在于: 无需硬件改造:将任意W…...

智慧医疗能源事业线深度画像分析(上)
引言 医疗行业作为现代社会的关键基础设施,其能源消耗与环境影响正日益受到关注。随着全球"双碳"目标的推进和可持续发展理念的深入,智慧医疗能源事业线应运而生,致力于通过创新技术与管理方案,重构医疗领域的能源使用模式。这一事业线融合了能源管理、可持续发…...
)
React Native 开发环境搭建(全平台详解)
React Native 开发环境搭建(全平台详解) 在开始使用 React Native 开发移动应用之前,正确设置开发环境是至关重要的一步。本文将为你提供一份全面的指南,涵盖 macOS 和 Windows 平台的配置步骤,如何在 Android 和 iOS…...

【入坑系列】TiDB 强制索引在不同库下不生效问题
文章目录 背景SQL 优化情况线上SQL运行情况分析怀疑1:执行计划绑定问题?尝试:SHOW WARNINGS 查看警告探索 TiDB 的 USE_INDEX 写法Hint 不生效问题排查解决参考背景 项目中使用 TiDB 数据库,并对 SQL 进行优化了,添加了强制索引。 UAT 环境已经生效,但 PROD 环境强制索…...

无法与IP建立连接,未能下载VSCode服务器
如题,在远程连接服务器的时候突然遇到了这个提示。 查阅了一圈,发现是VSCode版本自动更新惹的祸!!! 在VSCode的帮助->关于这里发现前几天VSCode自动更新了,我的版本号变成了1.100.3 才导致了远程连接出…...

2.Vue编写一个app
1.src中重要的组成 1.1main.ts // 引入createApp用于创建应用 import { createApp } from "vue"; // 引用App根组件 import App from ./App.vue;createApp(App).mount(#app)1.2 App.vue 其中要写三种标签 <template> <!--html--> </template>…...

测试markdown--肇兴
day1: 1、去程:7:04 --11:32高铁 高铁右转上售票大厅2楼,穿过候车厅下一楼,上大巴车 ¥10/人 **2、到达:**12点多到达寨子,买门票,美团/抖音:¥78人 3、中饭&a…...

【数据分析】R版IntelliGenes用于生物标志物发现的可解释机器学习
禁止商业或二改转载,仅供自学使用,侵权必究,如需截取部分内容请后台联系作者! 文章目录 介绍流程步骤1. 输入数据2. 特征选择3. 模型训练4. I-Genes 评分计算5. 输出结果 IntelliGenesR 安装包1. 特征选择2. 模型训练和评估3. I-Genes 评分计…...
相比,优缺点是什么?适用于哪些场景?)
Redis的发布订阅模式与专业的 MQ(如 Kafka, RabbitMQ)相比,优缺点是什么?适用于哪些场景?
Redis 的发布订阅(Pub/Sub)模式与专业的 MQ(Message Queue)如 Kafka、RabbitMQ 进行比较,核心的权衡点在于:简单与速度 vs. 可靠与功能。 下面我们详细展开对比。 Redis Pub/Sub 的核心特点 它是一个发后…...

Razor编程中@Html的方法使用大全
文章目录 1. 基础HTML辅助方法1.1 Html.ActionLink()1.2 Html.RouteLink()1.3 Html.Display() / Html.DisplayFor()1.4 Html.Editor() / Html.EditorFor()1.5 Html.Label() / Html.LabelFor()1.6 Html.TextBox() / Html.TextBoxFor() 2. 表单相关辅助方法2.1 Html.BeginForm() …...
