数据结构:堆和堆排序
数据结构:堆和堆排序
文章目录
- 数据结构:堆和堆排序
- 1.二叉树的存储结构
- 1.顺序结构
- 2.链式结构
- 2.堆
- 3.堆的实现
- 4.堆排序(选择排序中的一类)
- 1. 基本思想
- 2.代码实现
1.二叉树的存储结构
1.顺序结构
顺序结构存储就是使用数组来表示一棵二叉树,一般使用数组只适合表示完全二叉树,因为不是完全二叉树会有空间的浪费。而现实使用中只有堆才会使用数组来存储。二叉树顺序存储在物理上是一个数组,在逻辑上是一颗二叉树。
2.链式结构
二叉树的链式存储是使用链表来表示一棵二叉树,即用指针链接来指示元素的逻辑关系。 通常的方法是
链表中每个结点由三个域组成,数据域和左右指针域,左右指针分别用来给出该结点左孩子和右孩子所
在的链结点的存储地址 。
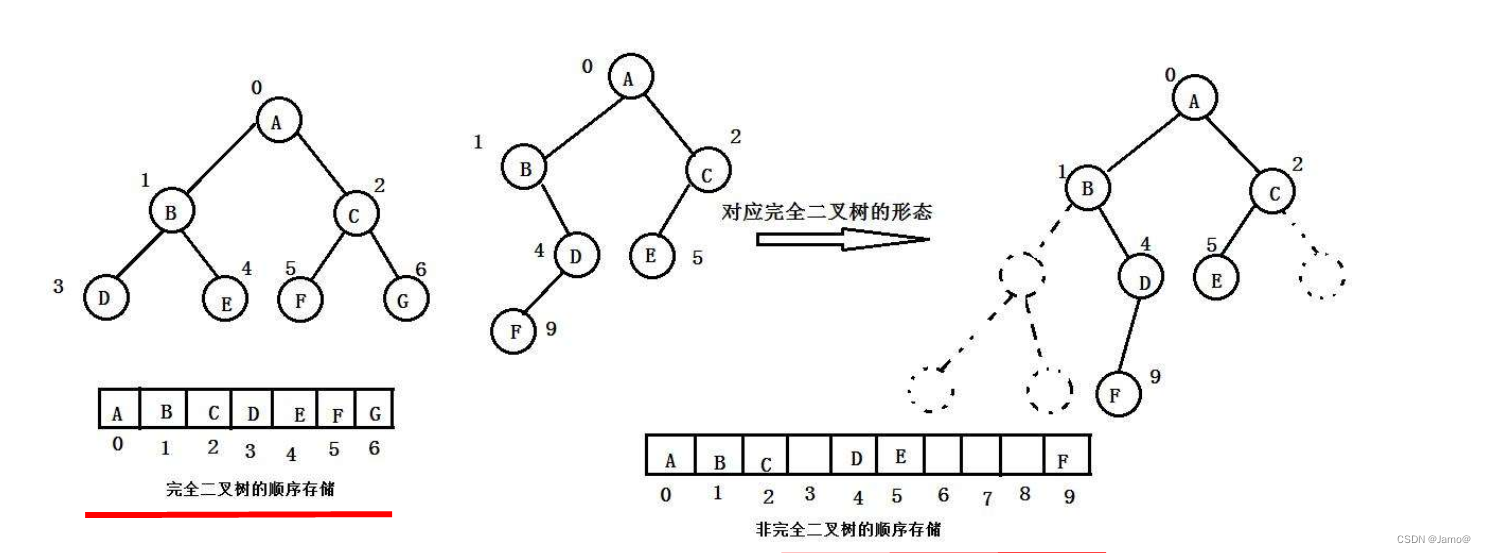
2.堆
堆实际上就是一棵完全二叉树:
其性质为:
- 堆中某个节点的值总是不大于或不小于其父节点的值;
- 堆总是一棵完全二叉树。
大堆和小堆:
- 每个节点的值都大于或等于其子节点的值,为大堆;反之为小堆。
3.堆的实现
#define _CRT_SECURE_NO_WARNINGS 1#include <stdio.h>
#include <stdlib.h>
#include <assert.h>
#include<stdbool.h>
// (大小)堆的实现(堆的结构与特点发现与数组下标有紧密关系)因此可以使用顺序表结构体
typedef int HPDataType;
typedef struct Heap
{HPDataType* a;int size;int capacity;
}Heap;// 堆的构建
void HeapCreate(Heap* hp);// 堆的销毁
void HeapDestory(Heap* hp);
// 向上调整
void AdjustUp(HPDataType* a, size_t childposition);// 堆的插入
void HeapPush(Heap* hp, HPDataType x);
// 向下调整
void AdjustDown(HPDataType* a, int size, size_t parentposition);// 堆的删除
void HeapPop(Heap* hp);// 取堆顶的数据
HPDataType HeapTop(Heap* hp);// 堆的数据个数
int HeapSize(Heap* hp);// 堆的判空
bool HeapEmpty(Heap* hp);
#include "Heap.h"// 堆的构建
void HeapCreate(Heap* hp)
{assert(hp);hp->a = NULL;hp->capacity = 0;hp->size = 0;
}
// 堆的销毁
void HeapDestory(Heap* hp)
{free(hp->a);hp->capacity = 0;hp->size = 0;hp = NULL;
}
// 向上调整
void AdjustUp(HPDataType* a, size_t childposition)
{assert(a);size_t parentposition = (childposition - 1) / 2;while (childposition > 0){// 小堆if (a[childposition] < a[parentposition]){// 交换孩子和父亲的值HPDataType tmp = a[childposition];a[childposition] = a[parentposition];a[parentposition] = tmp;childposition = parentposition;parentposition = (parentposition - 1) / 2;}else{return;}}
}
// 堆的插入
void HeapPush(Heap* hp, HPDataType x)
{assert(hp);// 检查容量if (hp->size == hp->capacity){int newcapacity = hp->capacity == 0 ? 4 : hp->capacity * 2;HPDataType* newa = (HPDataType*)realloc(hp->a, sizeof(HPDataType) * newcapacity);if (newa == NULL){perror("realloc fail");return;}hp->a = newa;hp->capacity = newcapacity;}hp->a[hp->size] = x;hp->size++;// 向上调整(可用递归可用循环,此处我们用循环实现)AdjustUp(hp->a, hp->size - 1);}
// 向下调整
void AdjustDown(HPDataType* a, int size, size_t parentposition)
{assert(a);size_t childposition = a[1] < a[2] ? 1 : 2;while (childposition < size){if (a[childposition] < a[parentposition])// 小堆{HPDataType tmp = a[childposition];a[childposition] = a[parentposition];a[parentposition] = tmp;parentposition = childposition;childposition = a[childposition * 2 + 1] < a[childposition * 2 + 2] ? childposition * 2 + 1 : childposition * 2 + 2;}else{break;}}
}// 堆的删除(删除堆顶元素)
void HeapPop(Heap* hp)
{assert(hp);if (hp->size == 0){printf("堆为空,无法删除\n");return;}HPDataType tmp = hp->a[0];hp->a[0] = hp->a[hp->size - 1];hp->size--;AdjustDown(hp->a, hp->size, 0);}
// 取堆顶的数据
HPDataType HeapTop(Heap* hp)
{assert(hp);return hp->a[0];
}
// 堆的数据个数
int HeapSize(Heap* hp)
{assert(hp);return hp->size;
}
// 堆的判空
bool HeapEmpty(Heap* hp)
{assert(hp);if (hp->size == 0){return true;}else{return false;}
}
4.堆排序(选择排序中的一类)
看到堆排序我们会想到是不是利用我们自己造轮子写出来的堆这个数据结构和接口函数来实现排序呢?
假设我们要对一个数组里的元素进行排序,我们可能想到这样做:
- 将数组里的元素通通插入到堆中,插入进去的元素自然就形成了一种排序结构。
- 再将堆里的数据取出来放回到原数组中从而进行排序。
弊端:这样进行‘’堆排序‘’实际上是十分复杂和浪费空间和时间的,这个方法前提下我们必须要先自己实现一个堆,再然后堆的构建也是要开辟内存空间的十分低效。
一次建堆的时间的复杂度是(向上调整建堆和向下调整建堆):
O ( N ∗ log N ) O(N*\log_{}{N}) O(N∗logN)
实际的堆排序:
记忆:升序建大堆,降序建小堆。
1. 基本思想
利用大顶堆(小顶堆)堆顶记录的是最大关键字(最小关键字)这一特性,使得每次从无序中选择最大记录(最小记录)变得简单。
① 将待排序的序列构造成一个==最大堆==,此时序列的最大值为根节点。
② 依次将根节点与待排序序列的最后一个元素交换。
③ 再维护从根节点到该元素的前一个节点为最大堆,**如此往复,最终得到一个递增序列**。
2.代码实现
// 向上调整
void AdjustUp(int* a, size_t childposition)
{assert(a);size_t parentposition = (childposition - 1) / 2;while (childposition > 0){// 大堆if (a[childposition] > a[parentposition]){// 交换孩子和父亲的值int tmp = a[childposition];a[childposition] = a[parentposition];a[parentposition] = tmp;childposition = parentposition;parentposition = (parentposition - 1) / 2;}else{return;}}
}void swap(int* start, int* end)
{int tmp = 0;tmp = *start;*start = *end;*end = tmp;
}// 堆排序
void HeapSort(int* a, int n)
{int i = 0;// 当数据个数大于1时才进行排序,否则直接就是有序的while (n > 1){// 建大堆使得最大的数位于堆顶部for (i = 1; i < n; i++){AdjustUp(a, i);}// 堆顶元素与堆最后一个元素交换位置swap(&a[0], &a[n - 1]);// 除去堆最后一个位置的元素重新建立大堆,如此往复,最终得到一个递增序列n--;}
}
#define _CRT_SECURE_NO_WARNINGS 1
#include<stdio.h>
#include<stdlib.h>
#include<assert.h>void HeapSort(int* a, int n);
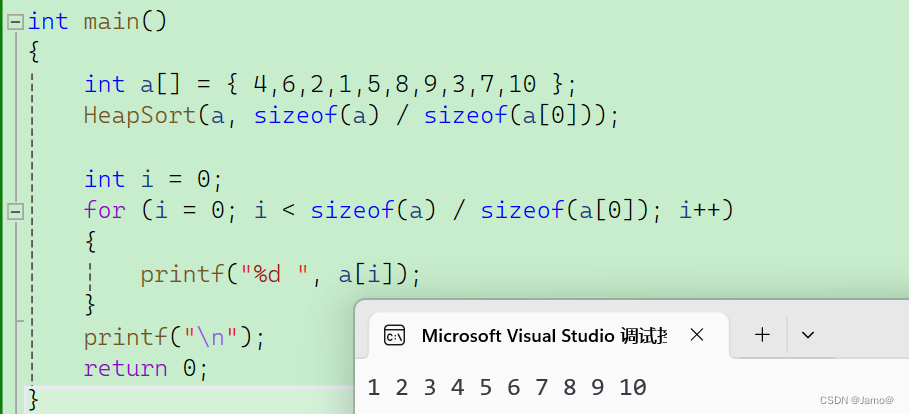
void AdjustUp(int* a, size_t childposition);int main()
{int a[] = { 4,6,2,1,5,8,9,3,7,10 };HeapSort(a, sizeof(a) / sizeof(a[0]));int i = 0;for (i = 0; i < sizeof(a) / sizeof(a[0]); i++){printf("%d ", a[i]);}printf("\n");return 0;
}

相关文章:

数据结构:堆和堆排序
数据结构:堆和堆排序 文章目录 数据结构:堆和堆排序1.二叉树的存储结构1.顺序结构2.链式结构 2.堆3.堆的实现4.堆排序(选择排序中的一类)1. 基本思想2.代码实现 1.二叉树的存储结构 1.顺序结构 顺序结构存储就是使用数组来表示一…...

力扣精选算法100题——水果成篮(滑动窗口专题)
本题链接👉水果成篮 第一步:了解题意 我就按照实例1来进行对这题的理解。 1代表种类类型,这个数组里面有2个种类类型 ps:种类1和种类2 ,只不过种类1是有2个水果,种类2有一个水果,共计3个水果。 本题需要解…...

【提示学习论文六】MaPLe: Multi-modal Prompt Learning论文原理
文章目录 MaPLe: Multi-modal Prompt Learning 多模式提示学习文章介绍动机MaPLe:Multi-modal Prompt Learning 模型结构1、Deep Language Prompting 深度语言提示2、Deep Vision Prompting 深度视觉提示3、Vision Language Prompt Coupling 视觉语言提示耦合提示耦合过程 实验…...
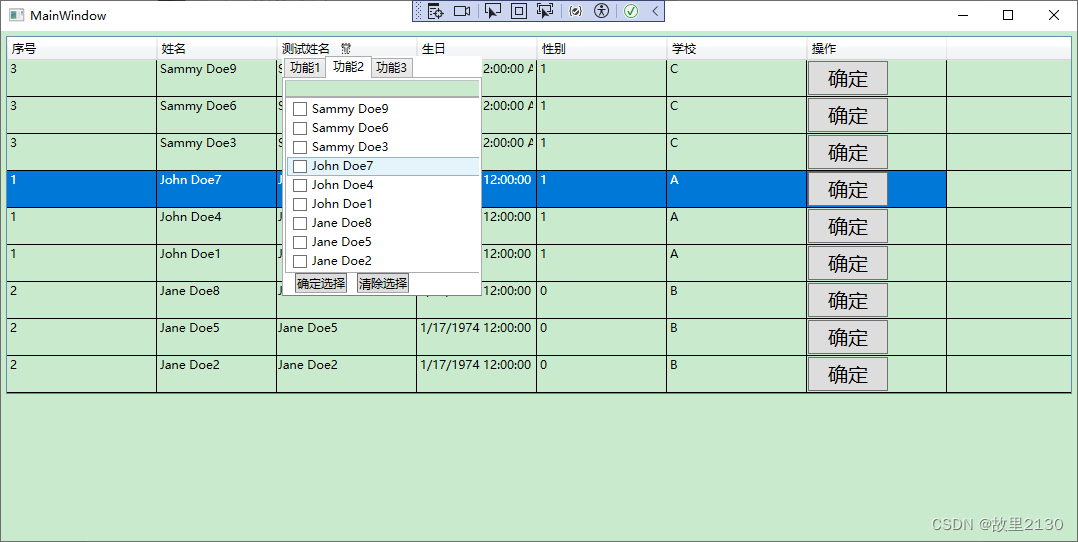
wpf使用Popup封装数据筛选框
(关注博主后,在“粉丝专栏”,可免费阅读此文) 类似于DevExpress控件的功能 这是DevExpress的winform筛选样式,如下: 这是DevExpress的wpf筛选样式,如下: 这是Excel的筛选样式,如下: 先看效果 本案例使用wpf原生控件封装,功能基本上都满足,只是颜色样式没有写…...

微信小程序 - 视图与逻辑 介绍
文章目录 视图与逻辑一、页面导航1、页面导航 - 声明式导航1.1 导航到tabBar页面1.2 导航到非tabBar页面1.3 后退导航 2、页面导航 - 编程式导航2.1 导航到tabBar页面2.2 导航到非tabBar页面2.3 后退导航 3、页面导航 - 导航传参3.1 声明式导航传参3.2 编程式导航传参3.3 在 on…...
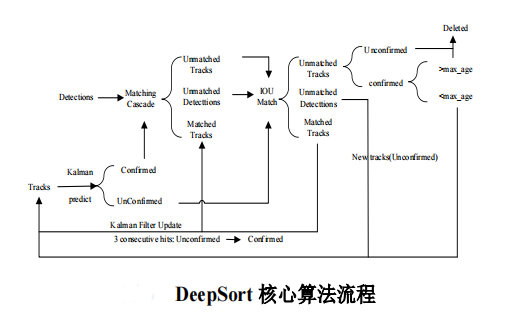
大创项目推荐 深度学习疫情社交安全距离检测算法 - python opencv cnn
文章目录 0 前言1 课题背景2 实现效果3 相关技术3.1 YOLOV43.2 基于 DeepSort 算法的行人跟踪 4 最后 0 前言 🔥 优质竞赛项目系列,今天要分享的是 🚩 **基于深度学习疫情社交安全距离检测算法 ** 该项目较为新颖,适合作为竞赛…...

c语言-库函数strstr()、strtok()、strerror()介绍
文章目录 前言一、库函数strstr()1.1 strstr()介绍1.2 strstr()模拟实现 二、库函数strtok()2.1 strtok()介绍 三、库函数strerror()3.1 strerror()介绍 总结 前言 本篇文章介绍c语言库函数strstr()、strtok()、strerror()的使用。 一、库函数strstr() 1.1 strstr()介绍 str…...
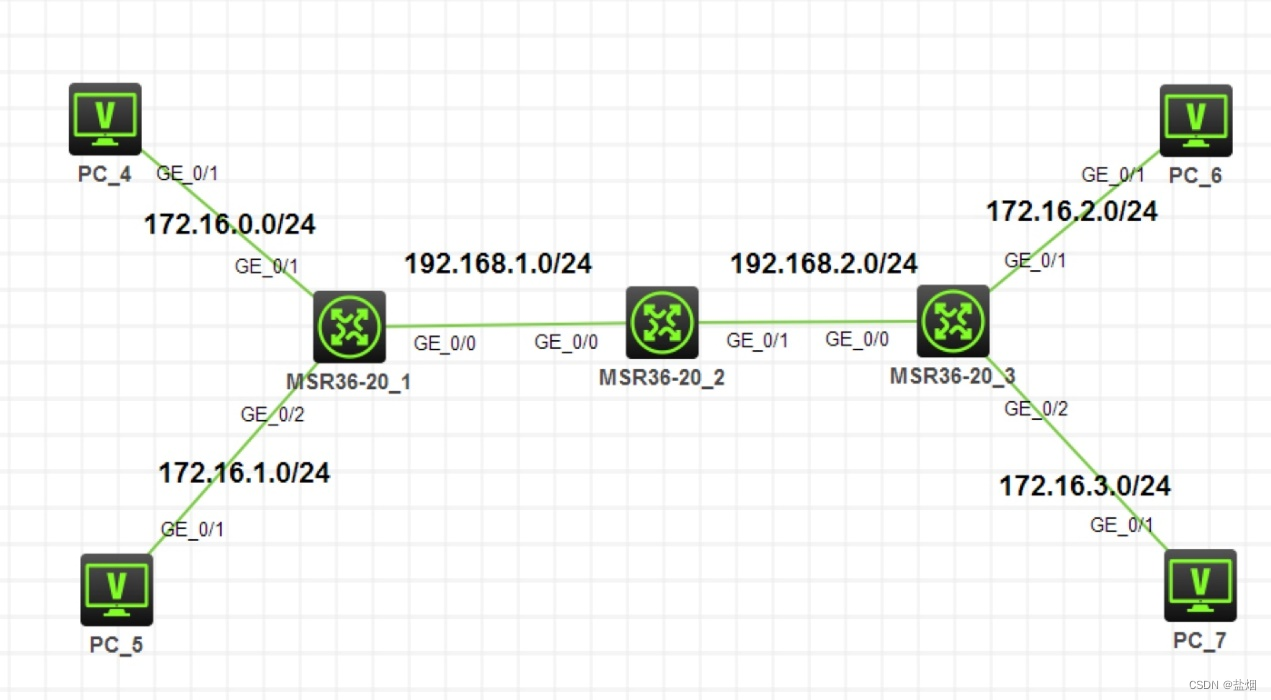
RIP【新华三与华为区别】
【介绍】 rip分为rip 1 与 rip 2 ,rip 2 是对 rip 1 的一种升级,rip 2 可以进行认证等功能 【命令】 新华三: [HC3-R1] rip #启用rip [HC3-R1-rip] version 2 #告知rip 版本号 [HC3-R1-rip] network 192.168.1.0 #宣告其网段 [HC3-R1-rip] …...

Python从入门到精通秘籍四
Python速成,知识点超详细,跟着这个系列边输入边学习体会吧! 一、Python的判断语句的综合案例 下面是一个使用代码示例来详细说明Python判断语句的综合案例,通过用户输入来实现简单的登录验证: # 提示用户输入用户名和密码 username = input("请输入用户名:")…...

rk3568下SoftBusDumpDeviceInfo执行错误—鸿蒙开发已解决
文章目录 项目场景:问题描述原因分析:解决方案:此Bug解决方案总结寄语项目场景: 最近也是遇到了这个问题,看到网上也有人在询问这个问题,本文总结了自己和其他人的解决经验,解决了rk3568下SoftBusDumpDeviceInfo执行错误的问题。 命令行运行 SoftBusDumpDeviceInfo,测…...

Vue 3 Composition API 详解
一、引言 在Vue 3中,引入了一个新的Composition API,旨在提供一种更灵活和可重用的方式来组织组件代码。Composition API基于函数式编程思想,允许开发者将逻辑和状态管理逻辑分离,使代码更加清晰和可维护。 二、Composition API…...
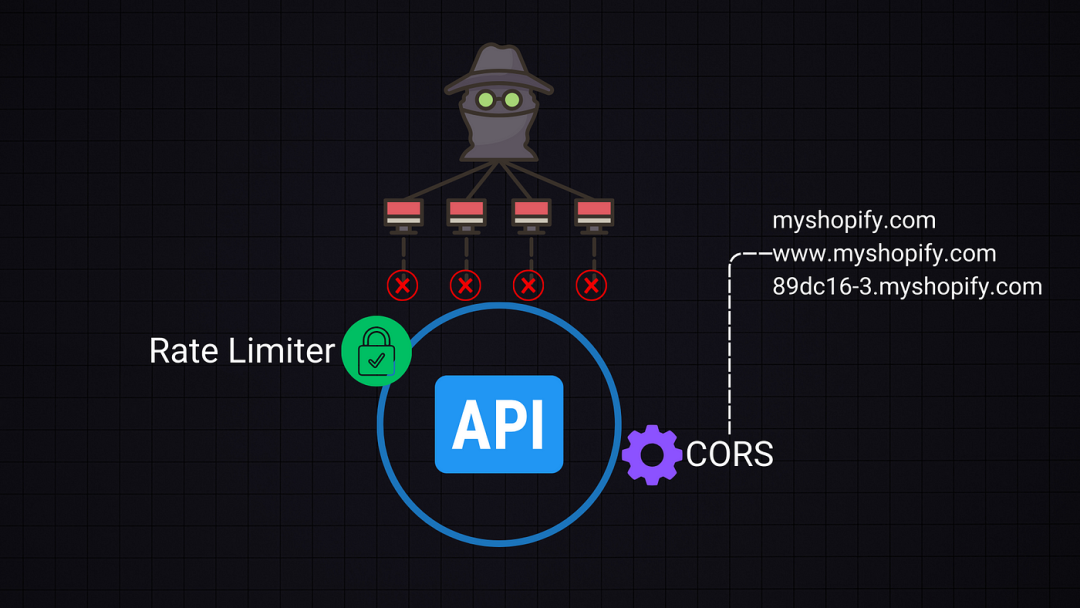
API设计:从基础到最佳实践
1*vWvkkgG6uvgmJT8GkId98A.png 在这次深入探讨中,我们将深入了解API设计,从基础知识开始,逐步进阶到定义出色API的最佳实践。 作为开发者,你可能对许多这些概念很熟悉,但我将提供详细的解释,以加深你的理解…...

每日汇评:由于中东危机削弱了风险偏好,欧元将在1.0900附近波动
随着中东危机的加深,欧元兑美元面临大幅抛售; 由于高通胀,欧洲央行决策者推迟了市场对早期降息的预期; 市场将受到周三公布的美国零售销售数据的影响; 持续的中东紧张局势增强了对避险资产的吸引力,而风险感…...

算法每日一题:删除子串后的字符串最小长度 | 栈 | 字符串
大家好,我是星恒 今天给大家带来的是一道另类的栈的应用 话不多说,我们直接来体验 题目:leetcode 2696 给你一个仅由 大写 英文字符组成的字符串 s 。你可以对此字符串执行一些操作,在每一步操作中,你可以从 s 中删除 …...
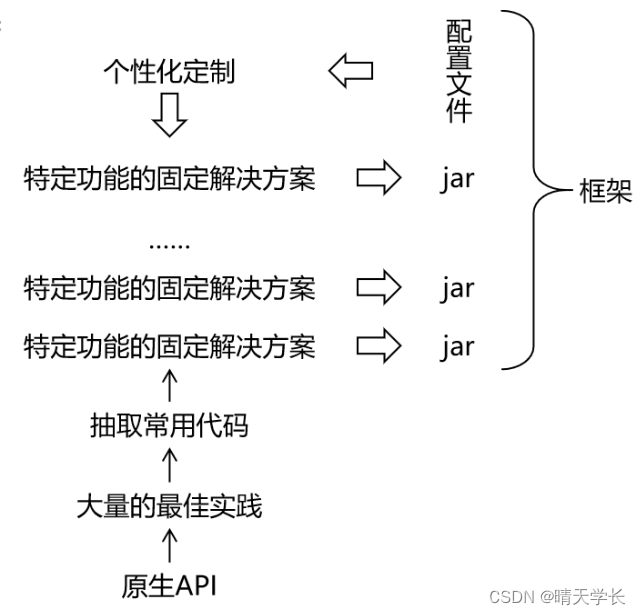
SpringFramework实战指南(一)
SpringFramework实战指南(一) 一、技术体系结构1.1 总体技术体系1.2 框架概念和理解 一、技术体系结构 1.1 总体技术体系 单一架构 一个项目,一个工程,导出为一个war包,在一个Tomcat上运行。也叫all in one。 单一架…...

AtCoder ABC198
本期F为群论题,很有难度。 C - Compass Walking 为了避免精度问题,采用二分推算。但是要小心结果为1的地方。 R 2 ∗ k 2 ≥ x 2 y 2 R^2*k^2\geq x^2y^2 R2∗k2≥x2y2 # -*- coding: utf-8 -*- # time : 2023/6/2 13:30 # file : atcoder.…...

phpinfo和php -m 加载的php.ini不一致
目的: 将phpinfo在web中展示的php.ini和在命令行中展示的php.ini加载路径设置一致。 原本的php.ini加载路劲是: /usr/local/lib/php.ini 解决思路: (1)which php 查看服务器加载的php的位置,这里原来是&a…...

121.买卖股票的最佳时机 122.买卖股票的最佳时机II
121.买卖股票的最佳时机 122.买卖股票的最佳时机II 121.买卖股票的最佳时机 力扣题目链接(opens new window) 给定一个数组 prices ,它的第 i 个元素 prices[i] 表示一支给定股票第 i 天的价格。 你只能选择 某一天 买入这只股票,并选择在 未来的某一…...

Spring Boot整理-Spring Boot是什么?
Spring Boot 是一个开源的 Java 基础框架,它旨在简化基于 Spring 的应用开发。其核心特点在于“约定优于配置”的设计哲学,意味着它提供了一系列默认配置,从而帮助开发者更快地启动和运行新的 Spring 应用。Spring Boot 的主要特点包括: 自动配置:Spring Boot 可以根据项目…...

【pytorch】Pytorch 中的 grid 与 各种变换
Pytorch 中的 grid 与 各种变换 数学原理 **单应性(Homography) : 也就是透视变换。**单应性最初用来研究欧几里得几何中的透视和投影,而单应性一词,从词源学上来说,大致意思是“相似的绘图”。单应性的概念被引入来…...

浅谈 React Hooks
React Hooks 是 React 16.8 引入的一组 API,用于在函数组件中使用 state 和其他 React 特性(例如生命周期方法、context 等)。Hooks 通过简洁的函数接口,解决了状态与 UI 的高度解耦,通过函数式编程范式实现更灵活 Rea…...

JavaSec-RCE
简介 RCE(Remote Code Execution),可以分为:命令注入(Command Injection)、代码注入(Code Injection) 代码注入 1.漏洞场景:Groovy代码注入 Groovy是一种基于JVM的动态语言,语法简洁,支持闭包、动态类型和Java互操作性,…...

Prompt Tuning、P-Tuning、Prefix Tuning的区别
一、Prompt Tuning、P-Tuning、Prefix Tuning的区别 1. Prompt Tuning(提示调优) 核心思想:固定预训练模型参数,仅学习额外的连续提示向量(通常是嵌入层的一部分)。实现方式:在输入文本前添加可训练的连续向量(软提示),模型只更新这些提示参数。优势:参数量少(仅提…...

Python:操作 Excel 折叠
💖亲爱的技术爱好者们,热烈欢迎来到 Kant2048 的博客!我是 Thomas Kant,很开心能在CSDN上与你们相遇~💖 本博客的精华专栏: 【自动化测试】 【测试经验】 【人工智能】 【Python】 Python 操作 Excel 系列 读取单元格数据按行写入设置行高和列宽自动调整行高和列宽水平…...

通过Wrangler CLI在worker中创建数据库和表
官方使用文档:Getting started Cloudflare D1 docs 创建数据库 在命令行中执行完成之后,会在本地和远程创建数据库: npx wranglerlatest d1 create prod-d1-tutorial 在cf中就可以看到数据库: 现在,您的Cloudfla…...

Nginx server_name 配置说明
Nginx 是一个高性能的反向代理和负载均衡服务器,其核心配置之一是 server 块中的 server_name 指令。server_name 决定了 Nginx 如何根据客户端请求的 Host 头匹配对应的虚拟主机(Virtual Host)。 1. 简介 Nginx 使用 server_name 指令来确定…...

Linux-07 ubuntu 的 chrome 启动不了
文章目录 问题原因解决步骤一、卸载旧版chrome二、重新安装chorme三、启动不了,报错如下四、启动不了,解决如下 总结 问题原因 在应用中可以看到chrome,但是打不开(说明:原来的ubuntu系统出问题了,这个是备用的硬盘&a…...

Kafka入门-生产者
生产者 生产者发送流程: 延迟时间为0ms时,也就意味着每当有数据就会直接发送 异步发送API 异步发送和同步发送的不同在于:异步发送不需要等待结果,同步发送必须等待结果才能进行下一步发送。 普通异步发送 首先导入所需的k…...

LLMs 系列实操科普(1)
写在前面: 本期内容我们继续 Andrej Karpathy 的《How I use LLMs》讲座内容,原视频时长 ~130 分钟,以实操演示主流的一些 LLMs 的使用,由于涉及到实操,实际上并不适合以文字整理,但还是决定尽量整理一份笔…...

基于PHP的连锁酒店管理系统
有需要请加文章底部Q哦 可远程调试 基于PHP的连锁酒店管理系统 一 介绍 连锁酒店管理系统基于原生PHP开发,数据库mysql,前端bootstrap。系统角色分为用户和管理员。 技术栈 phpmysqlbootstrapphpstudyvscode 二 功能 用户 1 注册/登录/注销 2 个人中…...
