计算机网络中的原码、反码、补码
写在前面
原码、反码、补码是计算机组成原理中的概念,是计算机网络的基础知识之一。这些概念是为了处理二进制数的符号位而引入的,常用于计算机中的整数运算,也常用于数据存储和传输等领域。因此,了解和掌握这些概念对于理解计算机网络和计算机组成原理都是非常重要的。
目录
写在前面
初步认识
发展历程
为什么要使用
有什么作用
如何计算 原码、反码、补码
例题
初步认识
在计算机中,整数通常使用原码、反码和补码表示。这三种表示方式都是用二进制位表示数字,但有不同的规则来表示正负号。
-
原码(sign-magnitude representation):最高位表示符号位,0表示正数,1表示负数,其余位表示数值大小。例如,+5的原码是00000101,-5的原码是10000101。
-
反码(ones' complement):正数的反码和原码相同,负数的反码是将原码中除符号位外的所有位按位取反。例如,+5的反码是00000101,-5的反码是11111010。
-
补码(two's complement):正数的补码和原码相同,负数的补码是将原码中除符号位外的所有位按位取反后加1。例如,+5的补码是00000101,-5的补码是11111011。
补码表示法是计算机中最常用的表示带符号整数的方式,其好处是可以用同一种方式进行加减运算,且减法可以转换成加法。例如,5-3可以转换成5+(-3),即00000101+11111101=00000010。此外,补码可以用来表示0,而原码和反码都会出现两个0的情况,分别对应+0和-0。
发展历程
在计算机的发展过程中,原码、反码和补码的概念逐渐形成和发展。
最早的计算机采用的是原码表示带符号数,即用二进制的最高位表示符号位,0表示正数,1表示负数。但是原码表示法存在着两个0的表示,即正数的0和负数的0。
为了解决这个问题,人们又发明了反码表示法。反码表示法是将负数的符号位不变,其他位按位取反,这样便能够解决正数和负数0的问题。但是反码表示法存在着减法运算的问题,即在进行减法运算时需要将被减数的符号位取反再加上减数的符号位。
后来,人们又发明了补码表示法。补码表示法是将负数的符号位不变,其他位按位取反再加1,这样既解决了0的问题,也能够解决减法运算的问题,因此成为了计算机中最常用的带符号整数表示法。
总的来说,原码、反码和补码是带符号整数的三种不同表示方法,随着计算机的发展,补码表示法逐渐成为了计算机中最常用的带符号整数表示法。
为什么要使用
计算机使用原码、反码和补码来表示带符号整数,主要是因为计算机中的运算是基于补码进行的。
在计算机中,加法和减法都是通过对二进制数的补码进行运算来实现的,这样可以将加法和减法转化为相同的运算。同时,补码的表示范围与原码相同,而且可以避免原码的符号位运算问题,使得运算更加方便。
另外,补码还有一个特点,就是它只有一个零,而原码和反码有正零和负零之分,这样会给计算带来很多问题,例如在比较大小时需要进行特殊的处理。而补码只有一个零,可以避免这些问题。
因此,使用原码、反码和补码可以使计算机进行带符号整数的运算更加方便、准确和统一,避免了很多计算问题。
有什么作用
常见的有符号整数表示方法包括原码、反码和补码。
1. 原码是一种最基本的数值表示方法,用于表示有符号的整数。在原码中,数值的最高位用于表示符号,0表示正数,1表示负数。例如,+7的原码为0000111,-7的原码为1000111。原码的表示方法最直观,计算机也最容易实现,但是它存在一些缺陷,主要体现在以下几个方面:
- 加减法不方便:在原码中,加减法需要分别考虑符号位和数值部分,这样计算起来比较繁琐。例如,对于+7和-5进行相加,需要先将它们的符号位进行运算,然后再对它们的数值部分进行运算,最终得到的结果为+2,其计算过程为:0000111 + 1000101 = 1001100,即7 - 5 = 2。
- 0有两种表示方法:在原码中,0既可以表示为0000000,也可以表示为1000000。这种情况下,计算机在进行运算时需要特殊处理,否则会导致运算结果错误。
- 为了解决原码存在的问题,人们提出了反码和补码的概念。
2. 反码是一种表示带符号整数的方式,它是在原码的基础上进行改进的。与原码相同的是,反码的二进制数最高位仍然用来表示符号,0表示正数,1表示负数。但是,对于负数的表示,反码做了一些特殊处理。
具体来说,正数的反码与原码相同。例如,+5的原码和反码都是00000101。但是,对于负数,反码是符号位不变,其余各位取反。例如,-5的原码是10000101,那么它的反码就是11111010。
反码的加减法只需要进行二进制的加法即可。例如,计算+3-2,可以将3和2的反码相加,再将结果取反得到最终的反码。具体过程如下:
+3的反码:00000011 -2的反码:11111101 相加得到:00000010 取反得到:11111101 所以,+3-2的结果的反码为11111101,对应的十进制数是-1。
反码的缺点是0还是有两种表示方法,分别是00000000和11111111。这是因为在原码中,0的符号位为0,在反码中,0的符号位为1,其余各位为0。因此,正零的反码为00000000,负零的反码为11111111。这种情况在计算机中可能会引起混淆,因此出现了补码的表示方式,它能够避免这个问题。
3. 补码是在反码的基础上进行了改进,主要解决了反码的问题,如反码的加减法中出现的溢出问题。补码的加减法与二进制的加减法是一致的,不需要考虑符号位。正数的补码和原码相同,负数的补码是其反码加1。
举个例子,假设要将数-5表示为补码形式。首先,将-5的绝对值表示为二进制形式,即0101,然后将其按位取反得到反码1010,最后将反码加1得到补码1011。因此,-5的补码为1011。
在计算机中,补码广泛应用于计算机算术运算和数据存储中。由于补码的加减法和二进制的加减法一致,可以方便地实现算术运算。此外,使用补码还可以避免0的两种表示方法,简化了计算机的处理。
总的来说,原码、反码和补码都是计算机中用于表示有符号整数的方法。它们的区别在于对于负数的表示方式不同,以及0的表示方法的差异。
原码是最简单的表示方法,使用二进制数的最高位表示符号。正数的原码和二进制数相同,负数的原码是其绝对值的二进制表示在最高位加上符号位1。原码的缺点是加减法不方便,需要单独考虑符号位,而且0有两种表示方法。
反码在原码的基础上改进,正数的反码和原码相同,负数的反码是符号位不变,其余各位取反。反码的加减法只需要进行二进制的加法即可,但是0还是有两种表示方法。
补码在反码的基础上进一步改进,正数的补码和原码相同,负数的补码是其反码加1。补码的加减法可以直接进行二进制的加法,且0只有一种表示方法,因此补码被广泛应用于计算机中。
在计算机中,一般使用补码表示有符号整数。因为补码具有很好的加减法性质和唯一的0表示方法,同时还能够方便地进行位运算和处理溢出等问题。
如何计算 原码、反码、补码
在计算机中的数据通常都是用二进制位来存储,其中的0和1都是比特,8个比特可以组成一个字节,一个字节可以表示256种不同的状态,可以用来表示整数、字符等数据类型。而原码、反码、补码,就是带有符号的整数。与字节有着密不可分的关系。
在计算之前我们先要学习进制转换
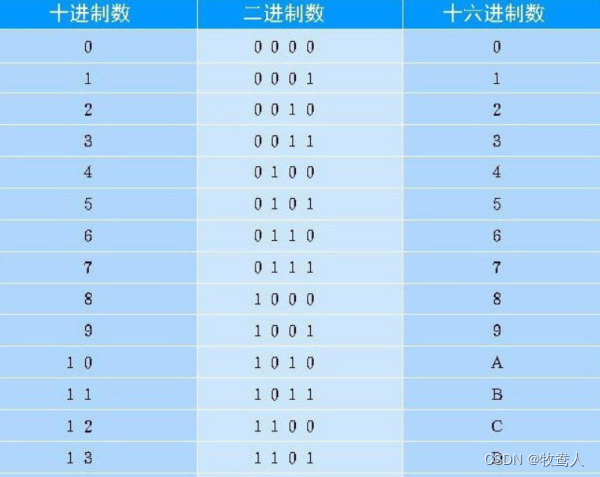
2的零次方=1,2的一次方=2,2的二次方=4,2的三次方=8,2的四次方=16,2的五次方=32,2的六次方=64,2的七次方=128,
00000000 ——对应上面的次方
2进制是由8个比特组成,每个比特以2的次方计算最为方便。比如56,先计算出56处于2的几次方之间。可以看出56大于32小于64,所以2的五次方是1,56-32=24 。24大于16小于32,所以2的四次方也是1,24-16=8,刚好等于2的三次方,所以56=2的三次方+2的四次方+2的五次方=00111000
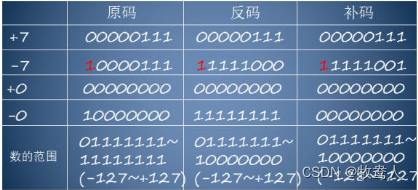
原码可以表示的数值是 -127到127 ,共计256个数。
反码也可以表示的数值是 -127到127 ,共计256个数。
补码可以表示的整数范围与原码和反码相同,都是在n个比特位中能表示的整数范围。但是,补码具有唯一的0表示法和良好的加减法性质,因此在计算机中被广泛应用。在使用补码表示法时,通常采用32位或64位的补码表示,这样可以表示更大的整数范围,同时保证计算机操作的高效性和精确性。
计算原码、反码、补码还需要掌握以下几个步骤:
- 确定数值的绝对值,转换成二进制数(忽略符号位)
- 确定数值的符号位,0表示正数,1表示负数
- 根据原码、反码、补码的定义,得到对应的码值
以十进制数-12为例,下面介绍如何计算原码、反码、补码:
- 确定数值的绝对值,即12的二进制表示为:1100
- 确定数值的符号位,因为-12是负数,所以符号位为1
- 计算原码:将符号位和绝对值合并,得到原码:1100 1100
- 计算反码:对于负数,反码是符号位不变,其余各位取反,得到反码:1111 0011
- 计算补码:对于负数,补码是反码加1,得到补码:1111 0100
同样地,以十进制数+12为例,下面介绍如何计算原码、反码、补码:
- 确定数值的绝对值,即12的二进制表示为:1100
- 确定数值的符号位,因为+12是正数,所以符号位为0
- 计算原码:将符号位和绝对值合并,得到原码:0100 1100
- 计算反码:对于正数,反码和原码相同,得到反码:0100 1100
- 计算补码:对于正数,补码和原码相同,得到补码:0100 1100
例题
- 假设要表示数值-23,我们要怎么算出他的原码、反码、补码
-23 的绝对值是23,转换成二进制是00010111.
符号位为1,表示负数,因此需要进行补码表示
因此-23的原码为 10010111
因此-23的反码为 11101000
因此-23的补码为 11101001
- 假设要表示数值+42,我们要怎么计算出他的原码、反码、补码
+42的绝对值为42,转换成二进制是00101010
符号位为0,表示正数
因此+42的原码为 00101010
因此+42的反码为 00101010
因此+42的补码为 00101010
- 假设要表示数值-223,我们要怎么计算出他的原码、反码、补码
-223的绝对值为223,转换成二进制是1101 1111
符号位为负,表示负数,因此需要进行补码表示
因此-223的原码为1000000011011111——因为-223是负数所以需要在字节前面加1,而223的8个比特的第8位已经是1了,所以我们要在给它一个字节;用1000000011011111的方式呈现它的原码
因此-223的反码为1111111100100000——因为反码是要将原码的1000000011011111因为在反码中,符号位不变,数值部分按位取反。
因此-223的补码为1111111100100001——因为负数补码需要在反码的基础上加1。
相关文章:

计算机网络中的原码、反码、补码
写在前面 原码、反码、补码是计算机组成原理中的概念,是计算机网络的基础知识之一。这些概念是为了处理二进制数的符号位而引入的,常用于计算机中的整数运算,也常用于数据存储和传输等领域。因此,了解和掌握这些概念对于理解计算机…...

七、Bean的实例化方式
Spring为Bean提供了多种实例化方式,通常包括4种方式。(也就是说在Spring中为Bean对象的创建准备了多种方案,目的是:更加灵活) 第一种:通过构造方法实例化第二种:通过简单工厂模式实例化第三种&…...
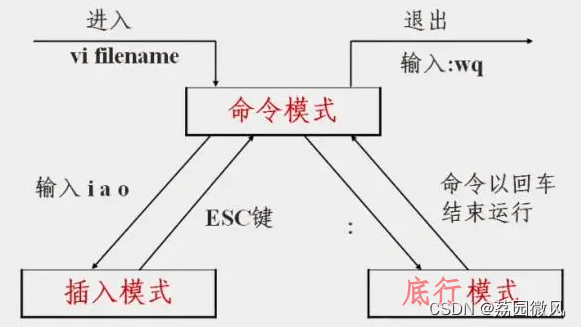
Windows程序员学习Linux环境下VI(VIM)编辑器的使用方法
我是荔园微风,作为一名在IT界整整25年的老兵,今天我们来重新审视一下Windows程序员如何学习Linux环境知识。由于很多程序在Windows环境下开发好后,还要部署到Linux服务器上去,所以作为Windows程序员有必要学习Linux环境的知识。VI…...

react入门篇
react入门篇前言一、目标二、项目环境三、实现过程(干货满满💥💥💥)1.创建react项目2.arco design UI库3.路由模块化4. 状态管理zustand5. axios6. 路由守卫前言 提示:这里可以添加本文要记录的大概内容&a…...

阿赵的MaxScript学习笔记分享九《可编辑多面体的操作》
大家好,我是阿赵。这是MaxScript学习笔记分享的第九篇,可编辑多面体的操作。不知不觉写了这么多篇了,应该还有几篇就写完了。自己给自己加一下油。 在3DsMax里面如果需要建模,一般使用到的塌陷方式有3种,可编辑的网格、…...
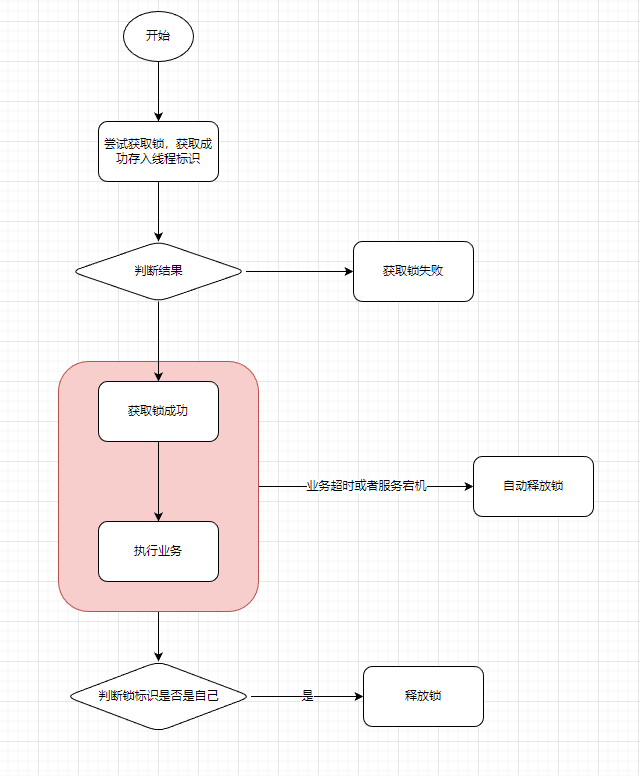
【Redis场景5】集群秒杀优化-分布式锁
集群环境下的秒杀问题 前序 【Redis场景1】用户登录注册 【Redis场景2】缓存更新策略(双写一致) 【Redis场景3】缓存穿透、击穿问题 【Redis场景拓展】秒杀问题-全局唯一ID生成策略 【Redis场景4】单机环境下秒杀问题 在单机环境下的并发问题,我们可以使用相关…...
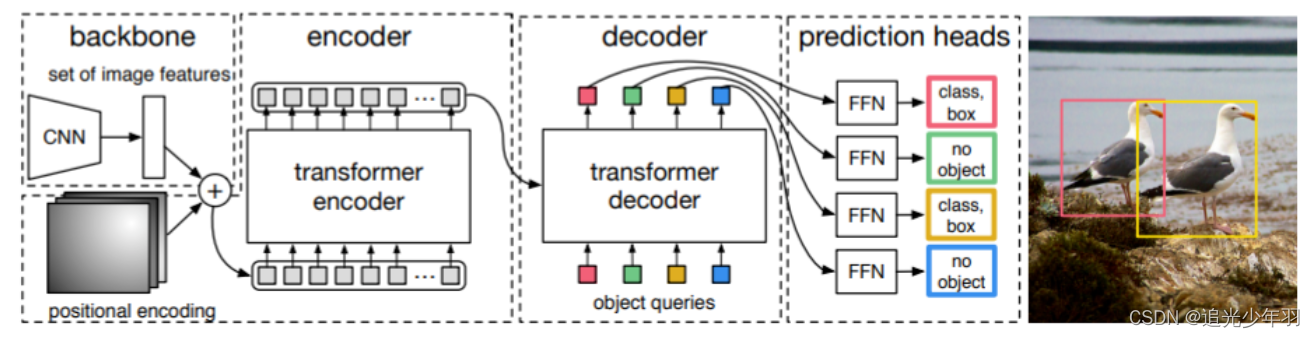
transformer目标检测开山之作detr
1. 将一个batch的图片输入backone获得feature。 (2,c,w,h)先输入resnet50中,得到(2,2048,w,h)。虽然这里channel不是256,但是在输入e…...
双指针法|位运算|离散化|区间合并
目录 双指针算法 位运算 离散化 序列合并 双指针算法 题目描述:1.输入n个单词,每个单词在输入的时候按空格隔开,之后打印出每个单词且换行 #include<iostream> #include <string>using namespace std; int main() {strin…...
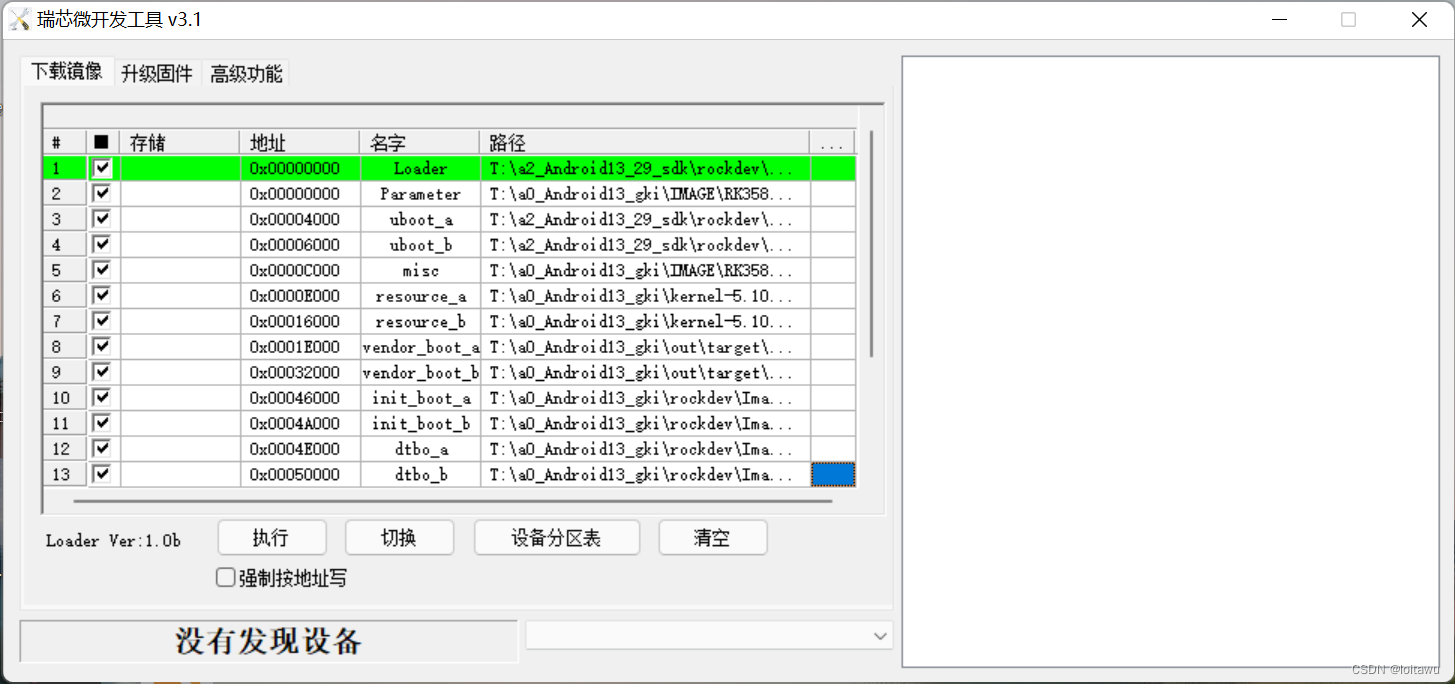
Rockchip Android13 GKI开发指南
Rockchip Android13 GKI开发指南 文章目录Rockchip Android13 GKI开发指南GKI介绍Google upstream kernel下载及编译Rockchip SDK中GKI相关目录介绍Rockchip GKI编译代码修改编译固件烧写KO编译及修改添加新的模块驱动的方法调试ko方法开机log确认uboot阶段Android阶段KO加载KO…...

手把手教你原生JavaScript打造丝滑流畅的轮播图,让你的网站瞬间提升用户体验!
简介 轮播图是网页设计中常见的交互组件之一,用于展示多张图片或内容,让用户能够方便地浏览、切换和选择。本文将介绍如何使用原生 JavaScript 手写一个简单的轮播图,并且通过代码解释实现细节。 目录 简介 HTML 结构 CSS 样式 JavaScr…...

git常用基本操作
克隆远程代码更新本地代码 git clone <-b | -branch> [branch name] [repository URL] git pull #拉取远程仓库代码,更新本地仓库 git merge <branch-name> #合并目标分支 建立本地仓库分支 git branch #查看当…...

剑指 Offer —— 数组和字符串
文章目录剑指 Offer 04. 二维数组中的查找代码实现解题方案 思路算法步骤剑指 Offer 05. 替换空格题目描述代码实现解题方案 思路算法步骤剑指 Offer 11. 旋转数组的最小数字 - 解决方案题目描述剑指 Offer 04. 二维数组中的查找 在一个 n * m 的二维数组中: 每…...
Java 字符编码
编码:数据存储进计算机中需要转换为二进制存储,这个过程就是编码。 解码:计算机读取数据并展示在页面上,需要将二进制转换为人类语言的过程,叫做解码。 乱码:如果编码和解码时使用的码表不一样,…...
ubuntu-9-安装chrony时间同步
使用chrony搭建时间同步服务器 [Linux系列]Chrony时间同步服务器 配置chrony服务,实现服务器时间自动同步 linux上内网环境配置NTP时间同步详解 经验体会:解决Ubuntu 18.04Windows双系统时间不同步的问题 1 时间同步 我们知道一台电脑主机,…...

CMMI流程规范—服务与维护
服务与维护(Service and Maintenance, SM)是指产品销售之后的客户服务和产品维护。客户服务和产品维护的宗旨就是提高客户对产品以及对开发方的满意度。服务与维护过程域是SPP模型的重要组成部分。本规范阐述了服务与维护过程域的两个主要规程࿱…...
【蓝桥杯集训12】DFS(3 / 5)
目录 842. 排列数字 - DFS按位置枚举 843. n-皇后问题 - DFS按行枚举 165. 小猫爬山 - DFS枚举小猫 1209. 带分数 - DFS 3502. 不同路径数 - 842. 排列数字 - DFS按位置枚举 活动 - AcWing 题目: 给你一个整数n 要求将1~n的所有排列情况列出 比如:…...
Elasticsearch:构建自动补全功能 - Autocomplete
什么是自动补全(autocomplete)功能呢?我们举一个很常见的例子。 每当你去谷歌并开始打字时,就会出现一个下拉列表,其中列出了建议。 这些建议与查询相关并帮助用户完成查询。 Autocomplete 正如维基百科所说的…...
One UI 5.1 更新来了
之前一直在关注One UI 5.0里提到的视频通话背景功能模块,结果5.0版本推送的时候没有引入,有先行者计划博主说是5.1里肯定会有的;前一两天One UI 5.1更新来了,然而该功能还是没有引入,表示很遗憾;本次更新新…...

Python学习笔记11:文件
文件 打开文件 函数open的参数mode的最常见取值 值描述‘r’读取模式(默认值)‘w’写入模式‘x’独占写入模式‘a’附加模式‘b’二进制模式(与其他模式结合使用)‘t’文本模式(默认值,与其他模式结合使…...

django-filter的使用
django-filter是一个通用的、可重用的应用程序,它可以减轻视图代码的编写工作量。具体来说,它允许用户根据模型的字段筛选查询集,并显示表单让他们这样做。 安装 pip install django-filter快速开始 在settings.py中添加如下配置: INSTAL…...

HTML 语义化
目录 HTML 语义化HTML5 新特性HTML 语义化的好处语义化标签的使用场景最佳实践 HTML 语义化 HTML5 新特性 标准答案: 语义化标签: <header>:页头<nav>:导航<main>:主要内容<article>&#x…...
)
Java 语言特性(面试系列2)
一、SQL 基础 1. 复杂查询 (1)连接查询(JOIN) 内连接(INNER JOIN):返回两表匹配的记录。 SELECT e.name, d.dept_name FROM employees e INNER JOIN departments d ON e.dept_id d.dept_id; 左…...
: K8s 核心概念白话解读(上):Pod 和 Deployment 究竟是什么?)
云原生核心技术 (7/12): K8s 核心概念白话解读(上):Pod 和 Deployment 究竟是什么?
大家好,欢迎来到《云原生核心技术》系列的第七篇! 在上一篇,我们成功地使用 Minikube 或 kind 在自己的电脑上搭建起了一个迷你但功能完备的 Kubernetes 集群。现在,我们就像一个拥有了一块崭新数字土地的农场主,是时…...

C++_核心编程_多态案例二-制作饮品
#include <iostream> #include <string> using namespace std;/*制作饮品的大致流程为:煮水 - 冲泡 - 倒入杯中 - 加入辅料 利用多态技术实现本案例,提供抽象制作饮品基类,提供子类制作咖啡和茶叶*//*基类*/ class AbstractDr…...

CTF show Web 红包题第六弹
提示 1.不是SQL注入 2.需要找关键源码 思路 进入页面发现是一个登录框,很难让人不联想到SQL注入,但提示都说了不是SQL注入,所以就不往这方面想了 先查看一下网页源码,发现一段JavaScript代码,有一个关键类ctfs…...

Matlab | matlab常用命令总结
常用命令 一、 基础操作与环境二、 矩阵与数组操作(核心)三、 绘图与可视化四、 编程与控制流五、 符号计算 (Symbolic Math Toolbox)六、 文件与数据 I/O七、 常用函数类别重要提示这是一份 MATLAB 常用命令和功能的总结,涵盖了基础操作、矩阵运算、绘图、编程和文件处理等…...

Java 二维码
Java 二维码 **技术:**谷歌 ZXing 实现 首先添加依赖 <!-- 二维码依赖 --><dependency><groupId>com.google.zxing</groupId><artifactId>core</artifactId><version>3.5.1</version></dependency><de…...

中医有效性探讨
文章目录 西医是如何发展到以生物化学为药理基础的现代医学?传统医学奠基期(远古 - 17 世纪)近代医学转型期(17 世纪 - 19 世纪末)现代医学成熟期(20世纪至今) 中医的源远流长和一脉相承远古至…...

基于 TAPD 进行项目管理
起因 自己写了个小工具,仓库用的Github。之前在用markdown进行需求管理,现在随着功能的增加,感觉有点难以管理了,所以用TAPD这个工具进行需求、Bug管理。 操作流程 注册 TAPD,需要提供一个企业名新建一个项目&#…...

【从零开始学习JVM | 第四篇】类加载器和双亲委派机制(高频面试题)
前言: 双亲委派机制对于面试这块来说非常重要,在实际开发中也是经常遇见需要打破双亲委派的需求,今天我们一起来探索一下什么是双亲委派机制,在此之前我们先介绍一下类的加载器。 目录 编辑 前言: 类加载器 1. …...
