【数据结构】二叉树-堆(top-k问题,堆排序,时间复杂度)
🌈个人主页:秦jh__https://blog.csdn.net/qinjh_?spm=1010.2135.3001.5343
🔥 系列专栏:《数据结构》https://blog.csdn.net/qinjh_/category_12536791.html?spm=1001.2014.3001.5482

目录
堆排序
第一种
编辑
第二种
TOP-K问题
建堆的时间复杂度
向下调整建堆的时间复杂度:
向上调整建堆的时间复杂度:
补充
前言
💬 hello! 各位铁子们大家好哇。
今日更新了堆排序,top-k问题和时间复杂度的内容
🎉 欢迎大家关注🔍点赞👍收藏⭐️留言📝
堆排序
第一种
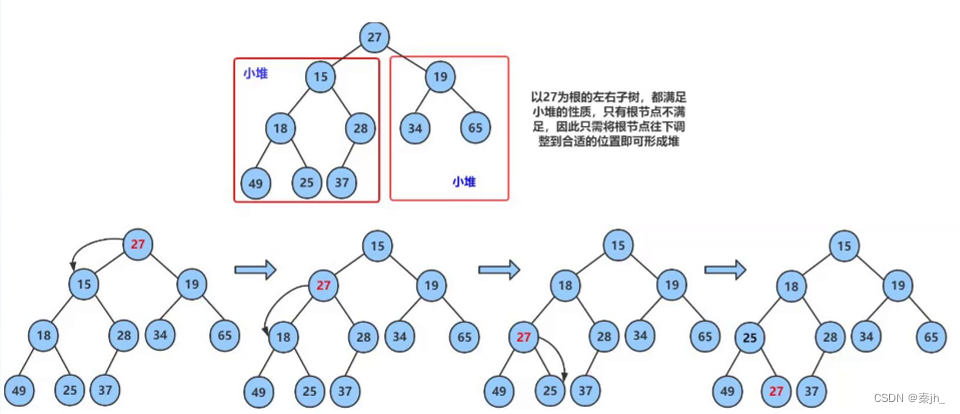
假如左右子树都是小堆,我们只需要进行向下调整建堆即可。
下方是建大堆:
思路分析:这里的向上和向下调整都是建大堆的。如果我们想进行升序排序,我们就得先建大堆。因为小堆的同一层中,无法进行比较。 接着,交换根结点和最后一个结点,这时就已经将最大的数排在末尾了。然后再从根结点向下调整建大堆,这时第二大的数就排在了根结点,再swap进行交换。end--表示不再对已排好的数进行操作。如此循环,即可进行升序。
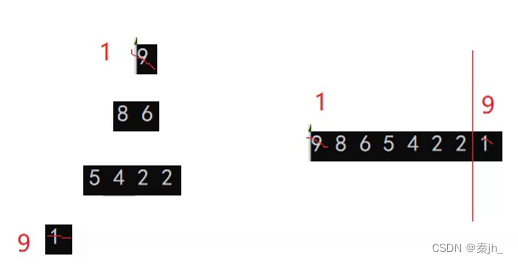
总结:如果是升序,就要建大堆。如果是降序,就要建小堆。 堆排序的本质是选择排序。
建堆的时间复杂度:N*logN
选数的时间复杂度:(N-1)*logN
第二种
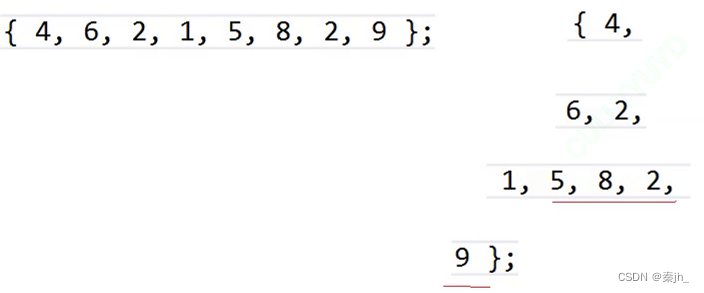
当左右子树不一定都是小堆时,我们就要进行从下往上的向下调整建堆。
方法:从倒数第一个非叶子开始(即最后一个节点的父亲)。9,2,8,5不用调,我们从1开始,1和9满足小堆。接着往前一位数到2,此时也满足小堆。继续往前到6,1和5比,1更小,所以1和6交换。接着来到4,交换后的1和2,1更小,4就和1交换
此方法的时间复杂度是O(N),并且此方式只需要一个向下调整,不需要多写一个向上调整函数。
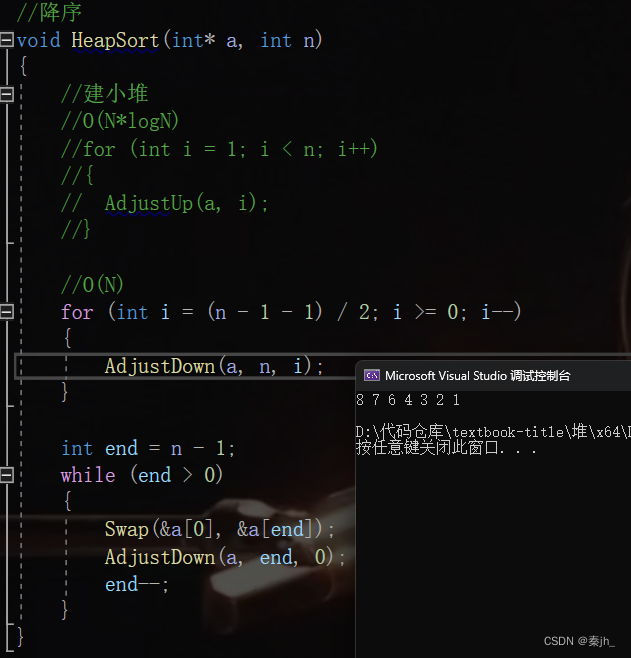
建小堆时,我们就会得到降序的数据。
TOP-K问题
TOP-K问题:即求数据结合中前K个最大的元素或者最小的元素,一般情况下数据量都比较大。
比如:专业前10名、世界500强、富豪榜、游戏中前100的活跃玩家等。
对于Top-K问题,能想到的最简单直接的方式就是排序,但是:如果数据量非常大,排序就不太可取了(可能数据都不能一下子全部加载到内存中)。最佳的方式就是用堆来解决,基本思路如下:
1.用数据集合中前K个元素来建堆
- 前k个最大的元素,则建小堆
- 前k个最小的元素,则建大堆
2.用剩余的N-K个元素依次与堆顶元素来比较,不满足则替换堆顶元素
将剩余N-K个元素依次与堆顶元素比完之后,堆中剩余的K个元素就是所求的前K个最小或者最大的元素。
举例如下:
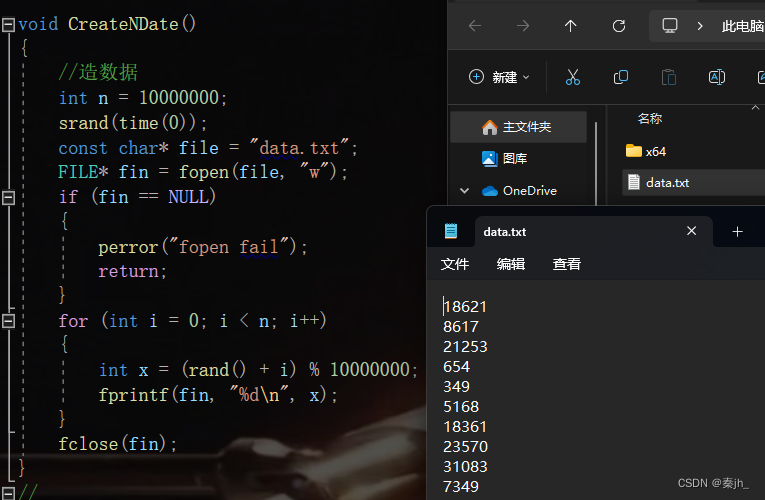
我们先生成一千万个随机数。
topk函数如下:
void PrintTopK(const char* file, int k)
{FILE* fout = fopen(file, "r");if (fout == NULL){perror("fopen fail");return;}//建一个k个数的小堆int* minheap = (int*)malloc(sizeof(int) * k);if (minheap == NULL){perror("malloc fail");return;}//读取前k个,建小堆for (int i = 0; i < k;i++){fscanf(fout, "%d", &minheap[i]);AdjustUp(minheap, i);}int x = 0;while (fscanf(fout, "%d", &x) != EOF){if (x > minheap[0]){minheap[0] = x;AdjustDown(minheap, k, 0);}}for (int i = 0; i < k; i++){printf("%d ", minheap[i]);}printf("\n");fclose(fout);
}我们先建立k个数的小堆,并将前k个数放进去。接着从第k+1开始的数开始与根结点比较,如果大于,就替换,然后进行向下调整,恢复成堆的形式。直到所有的数都比较完,我们就能找出前k个最大或最小的数了。
最后的运行结果如下:
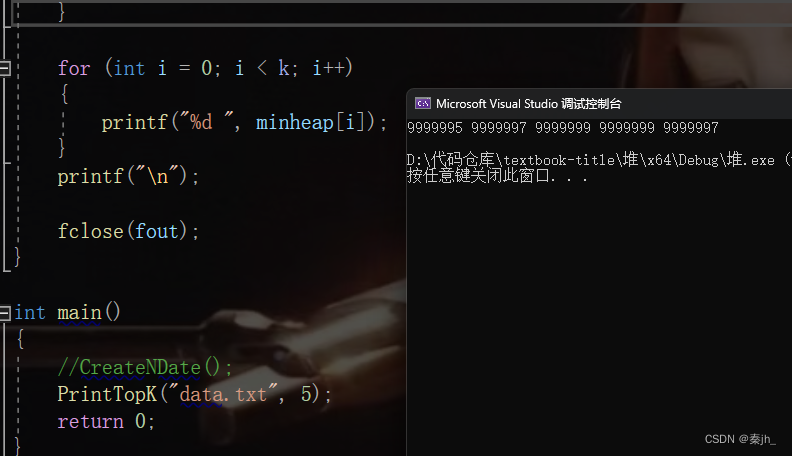
建堆的时间复杂度
向下调整建堆的时间复杂度:
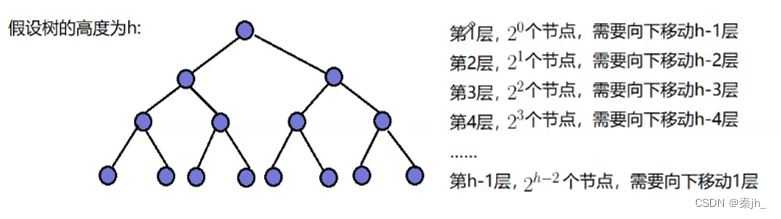
这里举例向下调整建堆的时间复杂度:
因为第h层是叶,就不需要向下移动了。具体计算过程如下图,因为是等差*等比,所以采用错位相减法进行计算。

因为最后的结果中的h是树的高度,不方便看出时间复杂度,替换成N(节点的个数)
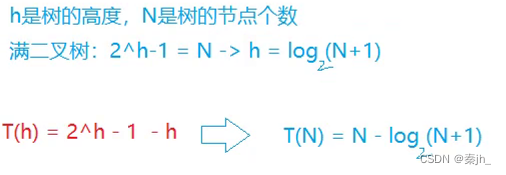
最终,时间复杂度是O(N)。
向上调整建堆的时间复杂度:
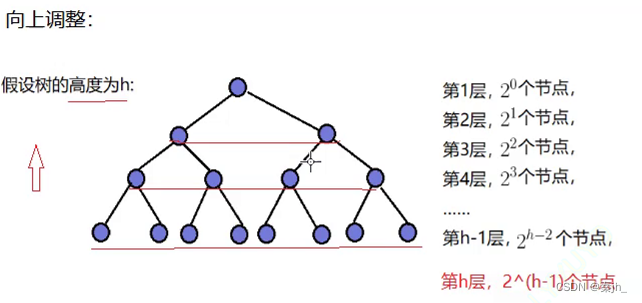


上方是求向上调整建堆时间复杂度的计算过程,原理与向下调整的一样。
最终的时间复杂度是:O(N*logN)
补充
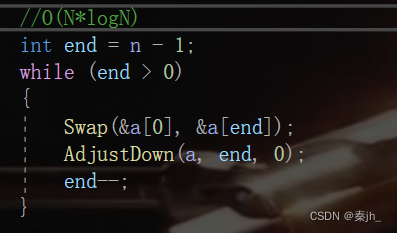
上方的过程的时间复杂度是O(N*logN),他跟上方的向上调整建堆相似,都是多*多,少*少的关系。因为最后一层有2^(h-1)个节点,每次交换后,最坏情况要向下调整(h-1)层,即多*多。第1层有一个节点,向下调整0层,即少*少。
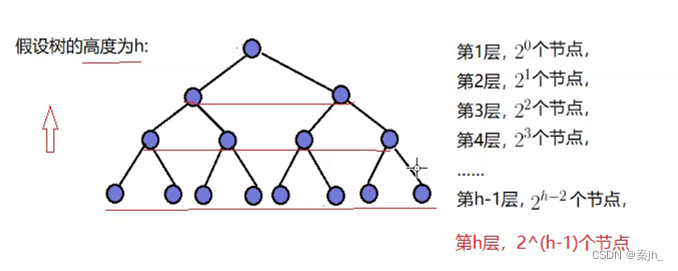
相关文章:

【数据结构】二叉树-堆(top-k问题,堆排序,时间复杂度)
🌈个人主页:秦jh__https://blog.csdn.net/qinjh_?spm1010.2135.3001.5343🔥 系列专栏:《数据结构》https://blog.csdn.net/qinjh_/category_12536791.html?spm1001.2014.3001.5482 目录 堆排序 第一种 编辑 第二种 …...

通过浏览器判断是否安装APP
场景 求在分享出来的h5页面中,有一个立即打开的按钮,如果本地安装了我们的app,那么点击就直接唤本地app,如果没有安装,则跳转到下载。 移动端 判断本地是否安装了app 首先我们可以确认的是,在浏览器中无…...

vivado Revision Control
2020.2 只需要git 管理 prj.xpr 和 prj.srcs/ https://china.xilinx.com/video/hardware/ip-revision-control.html Using Vivado Design Suite with Revision Control https://www.xilinx.com/video/hardware/vivado-design-suite-revision-control.html http://www.xi…...

【AI视野·今日Robot 机器人论文速览 第七十三期】Tue, 9 Jan 2024
AI视野今日CS.Robotics 机器人学论文速览 Tue, 9 Jan 2024 Totally 40 papers 👉上期速览✈更多精彩请移步主页 Daily Robotics Papers Digital Twin for Autonomous Surface Vessels for Safe Maritime Navigation Authors Daniel Menges, Andreas Von Brandis, A…...

java解析json复杂数据的第四种思路
文章目录 一、概述二、数据预览1. 接口json数据 三、代码实现1. 核心代码2. 字符串替换结果3. 运行结果 一、概述 接前两篇 java解析json复杂数据的两种思路 java解析json复杂数据的第三种思路 我们已经有了解析json数据的几种思路,下面介绍的方法是最少依赖情况下…...
【不用找素材】ECS 游戏Demo制作教程(1) 1.15
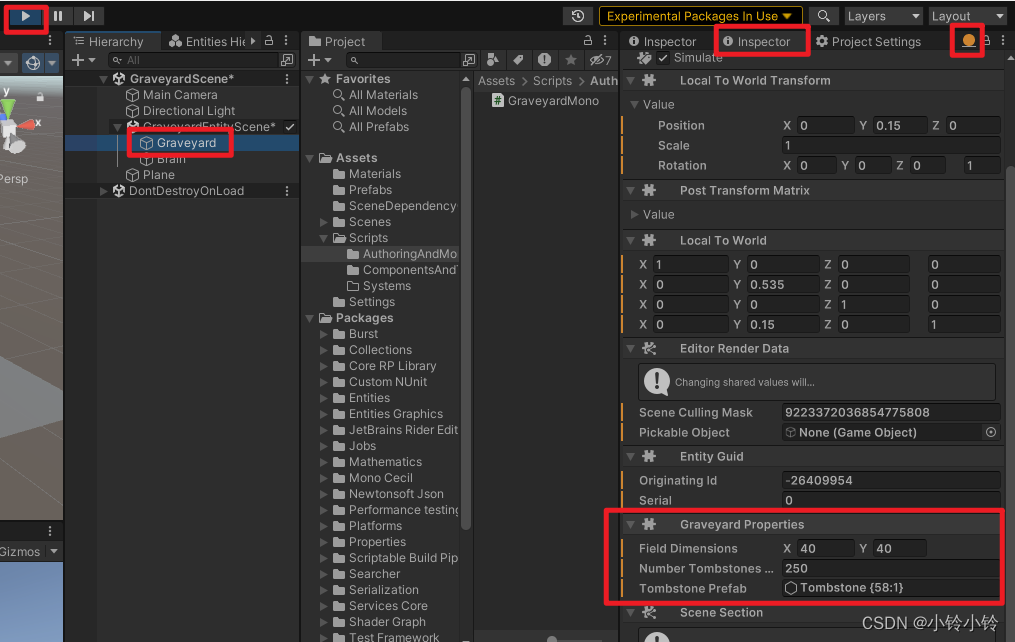
一、项目设置 版本:2022.2.0f1 (版本太低的话会安装不了ECS插件) 模板选择3D URP 进来后移除URP(因为并不是真的需要,但也不是完全不需要) Name: com.unity.entities.graphics Version: 1.0.0-exp.8 点击…...

Mysql的in与exits
Mysql的in与exits IN和EXISTS是MySQL中用于子查询的两种不同的条件操作符。它们在使用和实现上有一些区别。 IN 操作符: IN操作符用于判断一个值是否在一个集合内。它可以用于子查询中,检查主查询的某一列是否在子查询返回的结果集中。 SELECT colum…...
浅谈对Maven的理解
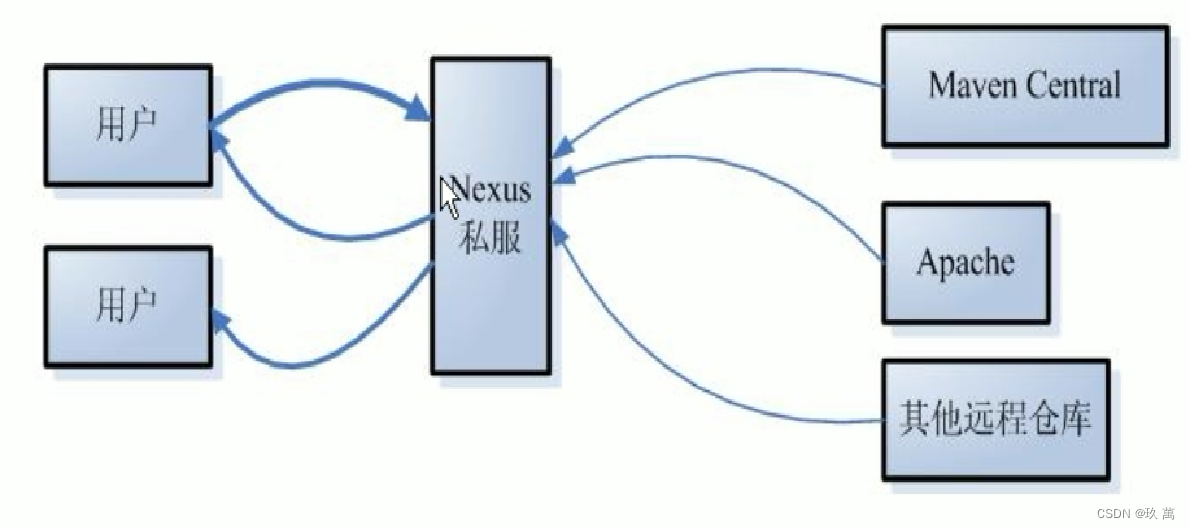
一、什么是Maven Maven——是Java社区事实标准的项目管理工具,能帮你从琐碎的手工劳动中解脱出来,帮你规范整个组织的构建系统。不仅如此,它还有依赖管理、自动生成项目站点等特性,已经有无数的开源项目使用它来构建项目并促进团队…...

【算法实验】实验2
实验2-1 二分搜索 【问题描述】给定一个包含 n 个元素有序的(升序)整型数组 nums 和一个目标值 target,要求实现搜索 nums 中的 target,如果目标值存在返回下标,否则返回 -1。题目保证nums中的所有元素都不重复。 【…...

杂记:使用 mac 和 windows 以及编辑器的总结
Chrome 扩展 Grammarly 语法检查 DM Integration Module idm 下载扩展 JSON Formatter json 格式化查看 uBlock Origin Ad block 油猴 任意网站都可以使用的脚本管理工具 Mac 快捷键整理 截图到剪贴板 shift command control 4 (不按 shift 存储为文件) 切换输入法…...

vue2使用qiankun微前端(跟着步骤走可实现)
需求:做一个vue2的微前端,以vue2为主应用,其他技术栈为子应用,比如vue3,本文章只是做vue2一套的微前端应用实现,之后解决的一些问题。vue3子应用可以看我另一篇vue3vitets实现qiankun微前端子应用-CSDN博客…...

1.C语言基础知识
这里写目录标题 1.第一个C语言程序2.注释3.标识符4.关键字5.数据类型6.变量7.常量8.运算符9.输入输出输入输出 1.第一个C语言程序 C语言的编程框架 #include <stdio.h> int main() {/* 我的第一个 C 程序 */printf("Hello, World! \n");return 0; }2.注释 单行…...
路由黑洞和黑洞路由的区别
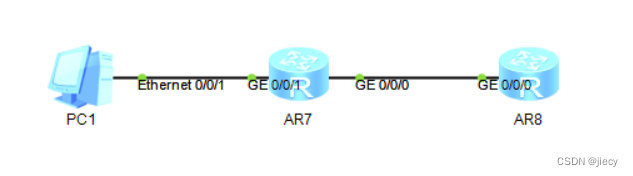
路由黑洞: 路由黑洞是一种现象,一般是在网络边界做汇总回程路由的时候产生的一种不太愿意出现的现象,就是汇总的时候有时会有一些不在内网中存在的网段,但是又包含在汇总后的网段中,如果在这个汇总的边界设备上同时还配…...

Golang 如何基于现有的 context 创建新的 context?
目录 基于现有的 context 创建新的 context 现有创建方法的问题 Go 1.21 中的 context.WithoutCancel 函数 Go 版本低于 1.21 该怎么办? 在 Golang 中,context 包提供了创建和管理上下文的功能。当需要基于现有的 context.Context 创建新的 context …...

【学习笔记】[AGC063E] Child to Parent
提供一个多项式做法。 分别设 f u , i , g u , i f_{u,i},g_{u,i} fu,i,gu,i表示以 u u u为根时, a u i a_ui aui和 a u ≥ i a_u\ge i au≥i的方案数,合并子树 v v v时,转移如下: f u , i ∑ f u , i − k r g v . k…...

sar 运行出错
手机上使用sar 使用sar工具报错 / # sar -I SUM 1 1 Cannot find the data collector (sadc) exec: No such file or directory Inconsistent input data解决方法:需要将 sadc sadf sar 三个bin同时推到/usr/bin/目录下 / # sar -I SUM 1 2 Linux 5.15.104-ab558…...

UE5 C++的TCP服务器与客户端
客户端.h 需要在Build.cs中加入模块:"Networking","Sockets","Json","JsonUtilities" // Fill out your copyright notice in the Description page of Project Settings.#pragma once#include "CoreMinimal.h" #include…...
nginx+lua配置,一个域名配置https,docker集群使用
没安装kua的先安装lua 没有resty.http模块的,许配置 nginxlua配置,一个域名配置https,docker集群使用,一个域名配置https管理整个集群 lua做转发(方向代理) 1、ad_load.lua文件 ngx.header.content_typ…...

jQuery 正则表达式 验证表单
文章目录 简介:什么是正则表达式以及作用:●文本框内容的验证:代码演示示例: 简介: jQuery Form插件是一个优秀的Ajax表单插件,可以非常容易地、无侵入地升级HTML表单以支持Ajax。jQuery Form有两个核心方法…...
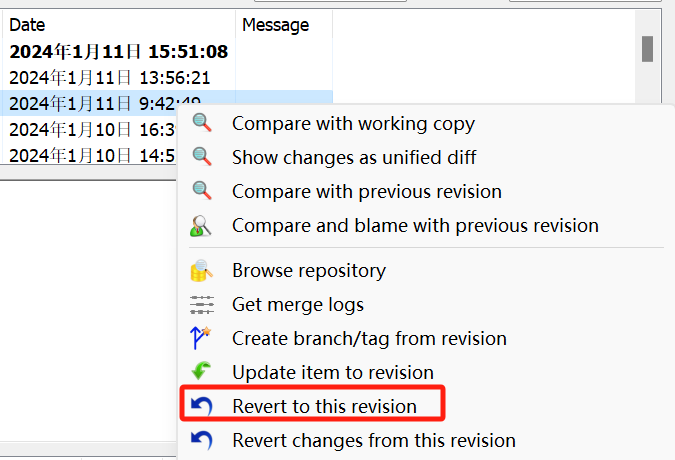
如何使用SVN查看旧版本
和目录 第一步:打开SVN客户端 第二步:浏览历史版本 第三步:还原历史版本 结论 Subversion (缩写为SVN)是一种常用的版本控制系统,它可以帮助团队协作开发软件项目。除了基本的版本控制功能外,SVN还提供了许多其他功…...

【Axure高保真原型】引导弹窗
今天和大家中分享引导弹窗的原型模板,载入页面后,会显示引导弹窗,适用于引导用户使用页面,点击完成后,会显示下一个引导弹窗,直至最后一个引导弹窗完成后进入首页。具体效果可以点击下方视频观看或打开下方…...

观成科技:隐蔽隧道工具Ligolo-ng加密流量分析
1.工具介绍 Ligolo-ng是一款由go编写的高效隧道工具,该工具基于TUN接口实现其功能,利用反向TCP/TLS连接建立一条隐蔽的通信信道,支持使用Let’s Encrypt自动生成证书。Ligolo-ng的通信隐蔽性体现在其支持多种连接方式,适应复杂网…...

iPhone密码忘记了办?iPhoneUnlocker,iPhone解锁工具Aiseesoft iPhone Unlocker 高级注册版分享
平时用 iPhone 的时候,难免会碰到解锁的麻烦事。比如密码忘了、人脸识别 / 指纹识别突然不灵,或者买了二手 iPhone 却被原来的 iCloud 账号锁住,这时候就需要靠谱的解锁工具来帮忙了。Aiseesoft iPhone Unlocker 就是专门解决这些问题的软件&…...

零基础在实践中学习网络安全-皮卡丘靶场(第九期-Unsafe Fileupload模块)(yakit方式)
本期内容并不是很难,相信大家会学的很愉快,当然对于有后端基础的朋友来说,本期内容更加容易了解,当然没有基础的也别担心,本期内容会详细解释有关内容 本期用到的软件:yakit(因为经过之前好多期…...

搭建DNS域名解析服务器(正向解析资源文件)
正向解析资源文件 1)准备工作 服务端及客户端都关闭安全软件 [rootlocalhost ~]# systemctl stop firewalld [rootlocalhost ~]# setenforce 0 2)服务端安装软件:bind 1.配置yum源 [rootlocalhost ~]# cat /etc/yum.repos.d/base.repo [Base…...

【Elasticsearch】Elasticsearch 在大数据生态圈的地位 实践经验
Elasticsearch 在大数据生态圈的地位 & 实践经验 1.Elasticsearch 的优势1.1 Elasticsearch 解决的核心问题1.1.1 传统方案的短板1.1.2 Elasticsearch 的解决方案 1.2 与大数据组件的对比优势1.3 关键优势技术支撑1.4 Elasticsearch 的竞品1.4.1 全文搜索领域1.4.2 日志分析…...

02.运算符
目录 什么是运算符 算术运算符 1.基本四则运算符 2.增量运算符 3.自增/自减运算符 关系运算符 逻辑运算符 &&:逻辑与 ||:逻辑或 !:逻辑非 短路求值 位运算符 按位与&: 按位或 | 按位取反~ …...

Vue 3 + WebSocket 实战:公司通知实时推送功能详解
📢 Vue 3 WebSocket 实战:公司通知实时推送功能详解 📌 收藏 点赞 关注,项目中要用到推送功能时就不怕找不到了! 实时通知是企业系统中常见的功能,比如:管理员发布通知后,所有用户…...
之(六) ——通用对象池总结(核心))
怎么开发一个网络协议模块(C语言框架)之(六) ——通用对象池总结(核心)
+---------------------------+ | operEntryTbl[] | ← 操作对象池 (对象数组) +---------------------------+ | 0 | 1 | 2 | ... | N-1 | +---------------------------+↓ 初始化时全部加入 +------------------------+ +-------------------------+ | …...

HTTPS证书一年多少钱?
HTTPS证书作为保障网站数据传输安全的重要工具,成为众多网站运营者的必备选择。然而,面对市场上种类繁多的HTTPS证书,其一年费用究竟是多少,又受哪些因素影响呢? 首先,HTTPS证书通常在PinTrust这样的专业平…...