【算法实验】实验2
实验2-1 二分搜索
【问题描述】给定一个包含 n 个元素有序的(升序)整型数组 nums 和一个目标值 target,要求实现搜索 nums 中的 target,如果目标值存在返回下标,否则返回 -1。题目保证nums中的所有元素都不重复。
【输入形式】输入的第1行中有1个数字n,表示数组的长度;第2行中有n个数字,表示数组的元素;第3行中有1个数字,表示要搜索的目标值。
【输出形式】输出1行中有1个数字,表示目标值在数组中出现的下标。
【样例输入1】
6
-5 0 1 5 10 12
0
【样例输出1】
1
【样例说明1】
0出现在nums中并且下标为1
【样例输入2】
6
-5 0 1 5 10 12
6
【样例输出1】
-1
【样例说明1】
6不存在于nums中因此输出-1
题目本身有序,无须排序
code1:
//实验2-1 二分
#include<bits/stdc++.h>
using namespace std;
const int N = 1e5 + 10;
int x;
int a[N];
int query(int low , int high)
{while(low < high){int mid = (low + high) >> 1;if(a[mid] == x){return mid;}else if(a[mid] > x){high = mid;}else{low = mid + 1; }}return -1;
}
int main()
{int n;cin >> n ;for(int i = 0 ; i < n ; i ++ ){cin >> a[i];}cin >> x;cout << query(0,n-1);return 0;} 个人更喜欢code2的风格:
//实验2-1 二分
#include<bits/stdc++.h>
using namespace std;
const int N = 1e5 + 10;
int x;
int a[N];
int query(int low , int high)
{while(low < high){int mid = (low + high) >> 1;if(x <= a[mid]) high = mid;else low = mid + 1;}return ( a[low] == x ? low : -1);
}
int main()
{int n;cin >> n ;for(int i = 0 ; i < n ; i ++ ){cin >> a[i];}cin >> x;cout << query(0,n-1);return 0;} 实验2-2 归并排序
MergeSort
【问题描述】给定一个长度为n的整数数组nums,要求必须使用【归并排序】的方法将该数组升序排序。
【输入形式】输入的第1行中有1个数字n,表示数组的长度;第2行中有n个数字,表示数组的元素
【输出形式】输出1行中有n个数字,表示按照升序排序后的数组,数字之间使用空格分割。
【样例输入】
5
35 28 9 87 56
【样例输出】
9 28 35 56 87
【说明】
1<=n<=10^4
0<=nums[i]<=10^5
#include<iostream>
using namespace std;
const int N = 1e4 + 10;
int a[N];void Merge(int l,int q,int r)
{int tmp[N];//临时数组 int n = r - l + 1; //长度 int k = 0; //临时数组Index int left = l; //左区间的第一个 int right = q + 1; //右区间的第一个 while(left <= q && right <= r ){tmp[ k ++ ] = a[left] <= a[right] ? a[left++] : a[right++];}while(left<=q)tmp[ k ++ ] = a[ left ++ ];while(right<=r)tmp[ k ++ ] = a[ right ++];//放过来 for(int i = 0 ; i < n ; i ++ ){a[l+i] = tmp[i];}
}
void MergeSort(int l,int r)
{if(l == r) return;else{int q = ( l + r ) / 2;MergeSort( l , q );MergeSort( q + 1 , r );Merge(l,q,r);}
}
int main()
{int n;cin >> n;for(int i = 0 ; i < n ; i ++ ){cin >> a[i];}MergeSort(0,n-1);for(int i = 0 ; i < n ; i ++ ){cout << a[i] <<" ";}return 0;
}实验2-3 寻找数组中的第k小元素
【问题描述】给定一个长度为n的整数数组nums和整数k,输出数组中的第k小元素。要求不能对数组排序,使用分治的思想求解。
【输入形式】输入的第1行中有1个数字n,表示数组的长度;第2行中有n个数字,表示数组的元素;第3行中有1个数字k。
【输出形式】输出1行中有1个数字,表示数组中的第k小元素。
【样例输入】
6
3 2 1 4 6 5
2
【样例输出】
2
【说明】
1<=k<=n<=10^4
10^-5<=nums[i]<=10^5
PS:这题我是真想排序输出啊

44是大量推导得出来的
递归法:
#include <algorithm>
#include<bits/stdc++.h>
using namespace std;
const int N=1e5+10;
int arr[N];
void quicksort(int arr[], int left, int right) { if (left >= right) { return; } int i = left, j = right, pivot = arr[left]; while (i < j) { while (i < j && arr[j] >= pivot) { j--; } if (i < j) { arr[i++] = arr[j]; } while (i < j && arr[i] < pivot) { i++; } if (i < j) { arr[j--] = arr[i]; } } arr[i] = pivot; quicksort(arr, left, i - 1); quicksort(arr, i + 1, right);
}
int main(){int n,k; cin >> n;for (int i=1;i<=n;++i){cin >> arr[i];}cin >> k;quicksort(arr, 1, n); printf("%d\n",arr[k]);return 0;
}实验2-4 整数因子分解问题
问题描述:
大于1 的正整数n 可以分解为:n=x1*x2*…*xm。
例如,当n=12 时,共有8 种不同的分解式:
12=12;
12=6*2;
12=4*3;
12=3*4;
12=3*2*2;
12=2*6;
12=2*3*2;
12=2*2*3 。
编程任务:
对于给定的正整数n,编程计算n 共有多少种不同的分解式。
数据输入:
由文件input.txt 给出输入数据。第一行有1 个正整数n (1≤n≤2000000000)。
结果输出:
将计算出的不同的分解式数输出到文件output.txt 。
输入文件示例 输出文件示例
input.txt output.txt
12 8
动态规划:
#include<bits/stdc++.h>
using namespace std;
const int N = 1e5 + 10;
int a[N],dp[N];
int k=0;
//初始化函数,找出n的所有约数
void init(int n)
{k = 0;int i = 1;for(i = 1; i < sqrt(n) ; i ++ ){if( n % i == 0 ) //如果是n的约数 存储 {a[ k ++ ] = i;a[ k ++ ] = n / i;}}if( i * i == n){a[ k ++ ] = i;}
}
void solve(int n){dp[0] = 1;for(int i = 1; i < k ; i ++ ){dp[i] = 0;for(int j = 0; j < i ; j ++ ){if( a[i] % a[j] ==0) //还能分解 {dp[i] += dp[j]; //+}}}
}
int main()
{int n;cin >> n;init(n); //初始化n的约数//记得排序sort( a , a + k );solve(n);cout << dp[k-1];return 0;
}实验2-5 矩阵乘法
【问题描述】要求必须使用【分治策略】计算两个矩阵的乘法。nxm阶的矩阵A乘以mxk阶的矩阵B得到的矩阵C是nxk阶的。
【输入形式】输入的第一行中有3个整数n, m,k,表示A矩阵是n行m列,B矩阵是m行k列。接下来的n行,每行m个数字,表示矩阵A中的元素。接下来的m行,每行k个元素,表示矩阵B中的元素。
【输出形式】输出矩阵C,一共n行,每行k个整数,整数之间以一个空格分开。
【样例输入】
3 2 3
1 1
1 1
1 1
1 1 1
1 1 1
【样例输出】
2 2 2
2 2 2
2 2 2
【说明】
1<=n,m,k<=100
矩阵中每个元素的绝对值<=1000
#include<iostream>
using namespace std;
const int N = 110;
int juz1[N][N];
int juz2[N][N];
int res[N][N];
int main()
{int x , y , k;cin >> x >> k >> y;//inputfor(int i = 1 ; i <= x; i ++){for(int j = 1 ; j <= k ; j ++ ){cin >> juz1[i][j]; }}for(int i = 1 ; i <= k; i ++){for(int j = 1 ; j <= y ; j ++ ){cin >> juz2[i][j]; }}//calufor(int i = 1 ; i <= x ; i ++ ){for(int j = 1; j <= y ; j ++){for(int w = 1; w <= k ; w ++){res[i][j] += juz1[i][k] * juz2[k][j];}}}//outputfor(int i = 1 ; i <= x ; i ++ ){for(int j = 1; j <= y ; j ++ ){cout << res[i][j] << " ";}cout <<"\n";}return 0;
}实验2-6 邮局选址问题
问题描述:
在一个按照东西和南北方向划分成规整街区的城市里,n 个居民点散乱地分布在不同的街区中。用x 坐标表示东西向,用y 坐标表示南北向。各居民点的位置可以由坐标(x,y) 表示。街区中任意2 点(x1,y1) 和(x2,y2) 之间的距离可以用数值|x1-x2|+|y1-y2| 度量。
居民们希望在城市中选择建立邮局的最佳位置,使n 个居民点到邮局的距离总和最小。
编程任务:
给定n 个居民点的位置,编程计算n 个居民点到邮局的距离总和的最小值。
数据输入:
由文件input.txt 提供输入数据。文件的第1 行是居民点数n,1<=n<=10000。接下来n 行是居民点的位置,每行2 个整数x 和y,-10000<=x,y<=10000。
结果输出:
程序运行结束时,将计算结果输出到文件output.txt 中。文件的第1 行中的数是n 个居民点到邮局的距离总和的最小值。
输入文件示例 输出文件示例
input.txt output.txt
5 10
1 2
2 2
1 3
3 -2
3 3
同货仓选址问题
code:
#include<iostream>
#include<algorithm>
using namespace std;
const int N = 1e5 + 10;
const int INF = 0x7f7f7f;int avex,avey;
int dis(int x){return abs( avex - x ) ;
}
int xx[N],yy[N];
int main()
{int n;cin >> n;for(int i = 1 ; i <= n ; i ++ ){cin >> xx[i] >> yy[i];}sort( xx + 1 , xx + n + 1);sort( yy + 1 , yy + n + 1);avex = xx[ n/2 + 1];avey = yy[ n/2 + 1];int mindis = 0;for(int i = 1 ; i <= n ; i ++ ){mindis += dis(xx[i]) + dis(yy[i]);}cout << mindis;return 0;
}相关文章:

【算法实验】实验2
实验2-1 二分搜索 【问题描述】给定一个包含 n 个元素有序的(升序)整型数组 nums 和一个目标值 target,要求实现搜索 nums 中的 target,如果目标值存在返回下标,否则返回 -1。题目保证nums中的所有元素都不重复。 【…...

杂记:使用 mac 和 windows 以及编辑器的总结
Chrome 扩展 Grammarly 语法检查 DM Integration Module idm 下载扩展 JSON Formatter json 格式化查看 uBlock Origin Ad block 油猴 任意网站都可以使用的脚本管理工具 Mac 快捷键整理 截图到剪贴板 shift command control 4 (不按 shift 存储为文件) 切换输入法…...

vue2使用qiankun微前端(跟着步骤走可实现)
需求:做一个vue2的微前端,以vue2为主应用,其他技术栈为子应用,比如vue3,本文章只是做vue2一套的微前端应用实现,之后解决的一些问题。vue3子应用可以看我另一篇vue3vitets实现qiankun微前端子应用-CSDN博客…...

1.C语言基础知识
这里写目录标题 1.第一个C语言程序2.注释3.标识符4.关键字5.数据类型6.变量7.常量8.运算符9.输入输出输入输出 1.第一个C语言程序 C语言的编程框架 #include <stdio.h> int main() {/* 我的第一个 C 程序 */printf("Hello, World! \n");return 0; }2.注释 单行…...
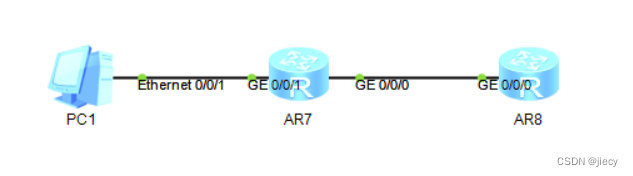
路由黑洞和黑洞路由的区别
路由黑洞: 路由黑洞是一种现象,一般是在网络边界做汇总回程路由的时候产生的一种不太愿意出现的现象,就是汇总的时候有时会有一些不在内网中存在的网段,但是又包含在汇总后的网段中,如果在这个汇总的边界设备上同时还配…...

Golang 如何基于现有的 context 创建新的 context?
目录 基于现有的 context 创建新的 context 现有创建方法的问题 Go 1.21 中的 context.WithoutCancel 函数 Go 版本低于 1.21 该怎么办? 在 Golang 中,context 包提供了创建和管理上下文的功能。当需要基于现有的 context.Context 创建新的 context …...

【学习笔记】[AGC063E] Child to Parent
提供一个多项式做法。 分别设 f u , i , g u , i f_{u,i},g_{u,i} fu,i,gu,i表示以 u u u为根时, a u i a_ui aui和 a u ≥ i a_u\ge i au≥i的方案数,合并子树 v v v时,转移如下: f u , i ∑ f u , i − k r g v . k…...

sar 运行出错
手机上使用sar 使用sar工具报错 / # sar -I SUM 1 1 Cannot find the data collector (sadc) exec: No such file or directory Inconsistent input data解决方法:需要将 sadc sadf sar 三个bin同时推到/usr/bin/目录下 / # sar -I SUM 1 2 Linux 5.15.104-ab558…...

UE5 C++的TCP服务器与客户端
客户端.h 需要在Build.cs中加入模块:"Networking","Sockets","Json","JsonUtilities" // Fill out your copyright notice in the Description page of Project Settings.#pragma once#include "CoreMinimal.h" #include…...
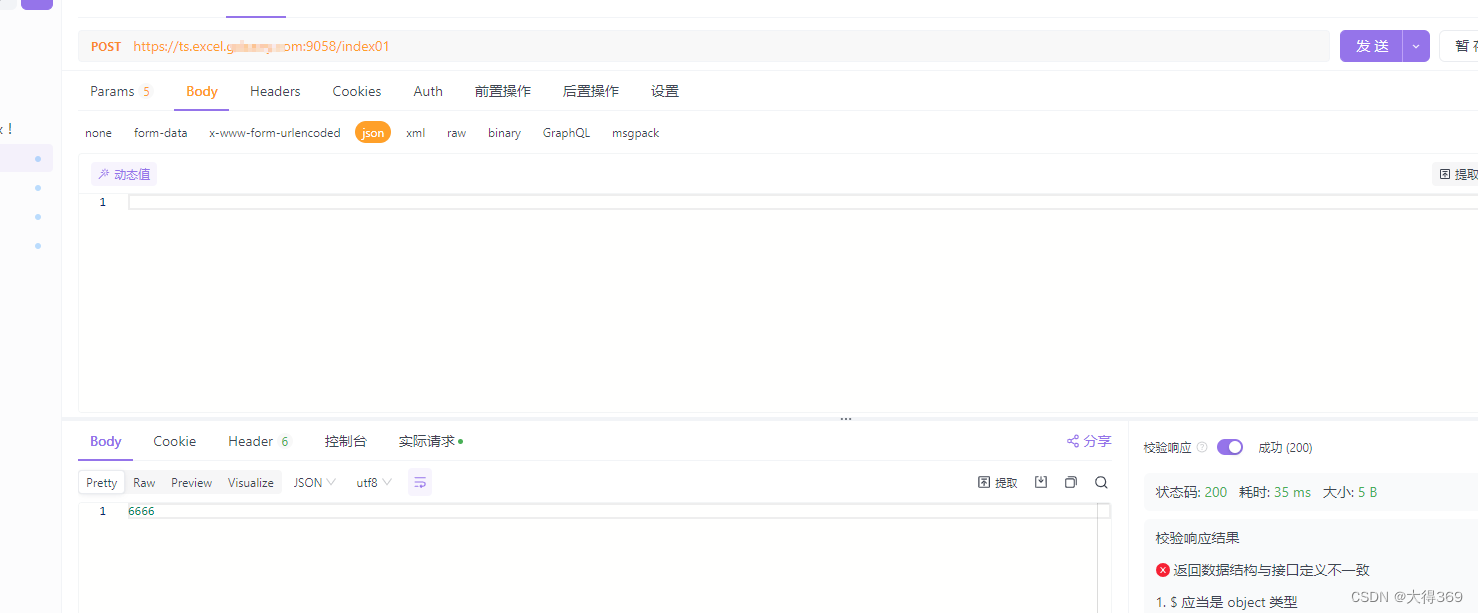
nginx+lua配置,一个域名配置https,docker集群使用
没安装kua的先安装lua 没有resty.http模块的,许配置 nginxlua配置,一个域名配置https,docker集群使用,一个域名配置https管理整个集群 lua做转发(方向代理) 1、ad_load.lua文件 ngx.header.content_typ…...

jQuery 正则表达式 验证表单
文章目录 简介:什么是正则表达式以及作用:●文本框内容的验证:代码演示示例: 简介: jQuery Form插件是一个优秀的Ajax表单插件,可以非常容易地、无侵入地升级HTML表单以支持Ajax。jQuery Form有两个核心方法…...
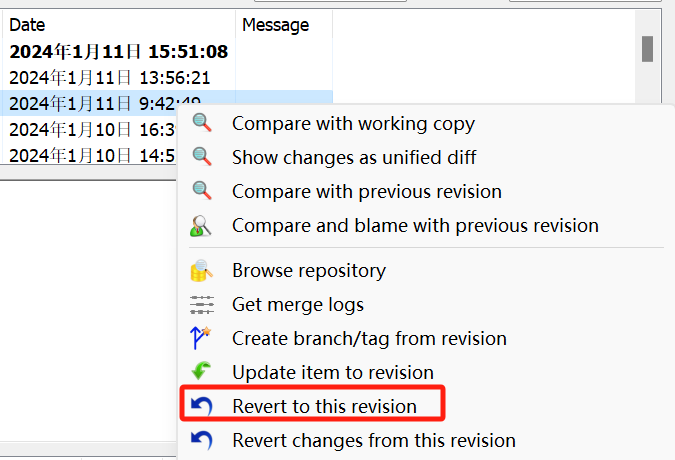
如何使用SVN查看旧版本
和目录 第一步:打开SVN客户端 第二步:浏览历史版本 第三步:还原历史版本 结论 Subversion (缩写为SVN)是一种常用的版本控制系统,它可以帮助团队协作开发软件项目。除了基本的版本控制功能外,SVN还提供了许多其他功…...
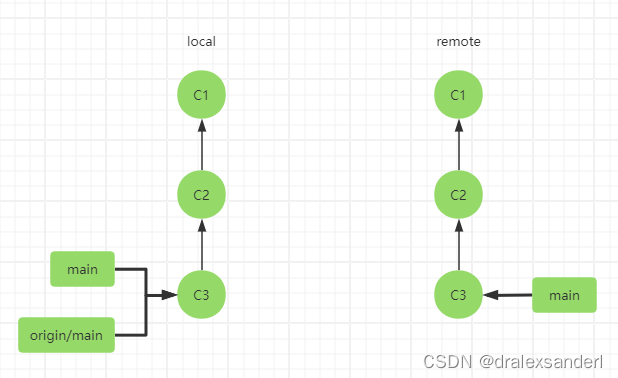
使用 GitHub 远程仓库
使用 GitHub 远程仓库 GitHub 是最大的 Git 版本库托管商,是成千上万的开发者和项目能够合作进行的中心。 大部分 Git 版本库都托管在 GitHub,很多开源项目使用 GitHub 实现 Git 托管、问题追踪、代码审查以及其它事情。本篇文章主要带大家上手 GitHub …...

关键词提取
在自然语言处理领域中,处理海量文本信息的关键在于把用户关心的问题提取出来。而关键词是能够表达文档中心内容的词语,更是表达文档主题的最小单位。因此,文本关键词的提取对于文本信息的理解是至关重要的。 关键词提取是文本挖掘领域下的一个…...
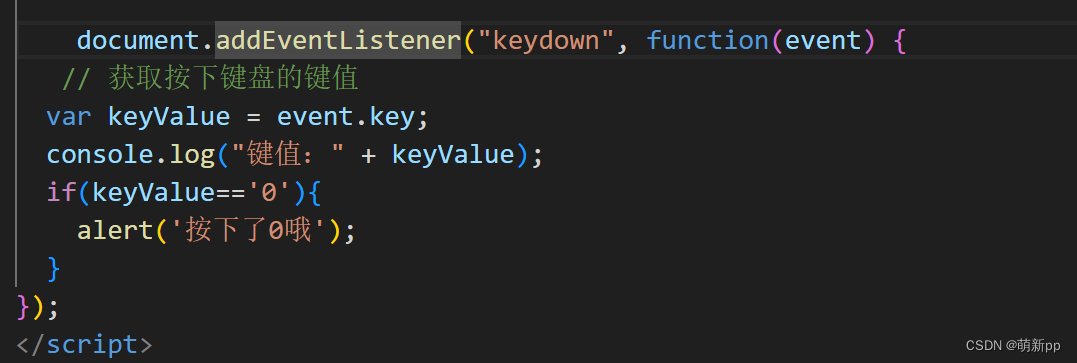
web开发学习笔记(2.js)
1.引入 2.js的两种引入方式 3.输出语句 4.全等运算符 5.定义函数 6.数组 7.数组属性 8.字符串对象的对应方法 9.自定义对象 10.json对象 11.bom属性 12.window属性 13.定时刷新时间 14.跳转网址 15.DOM文档对象模型 16.获取DOM对象,根据DOM对象来操作网页 如下图…...
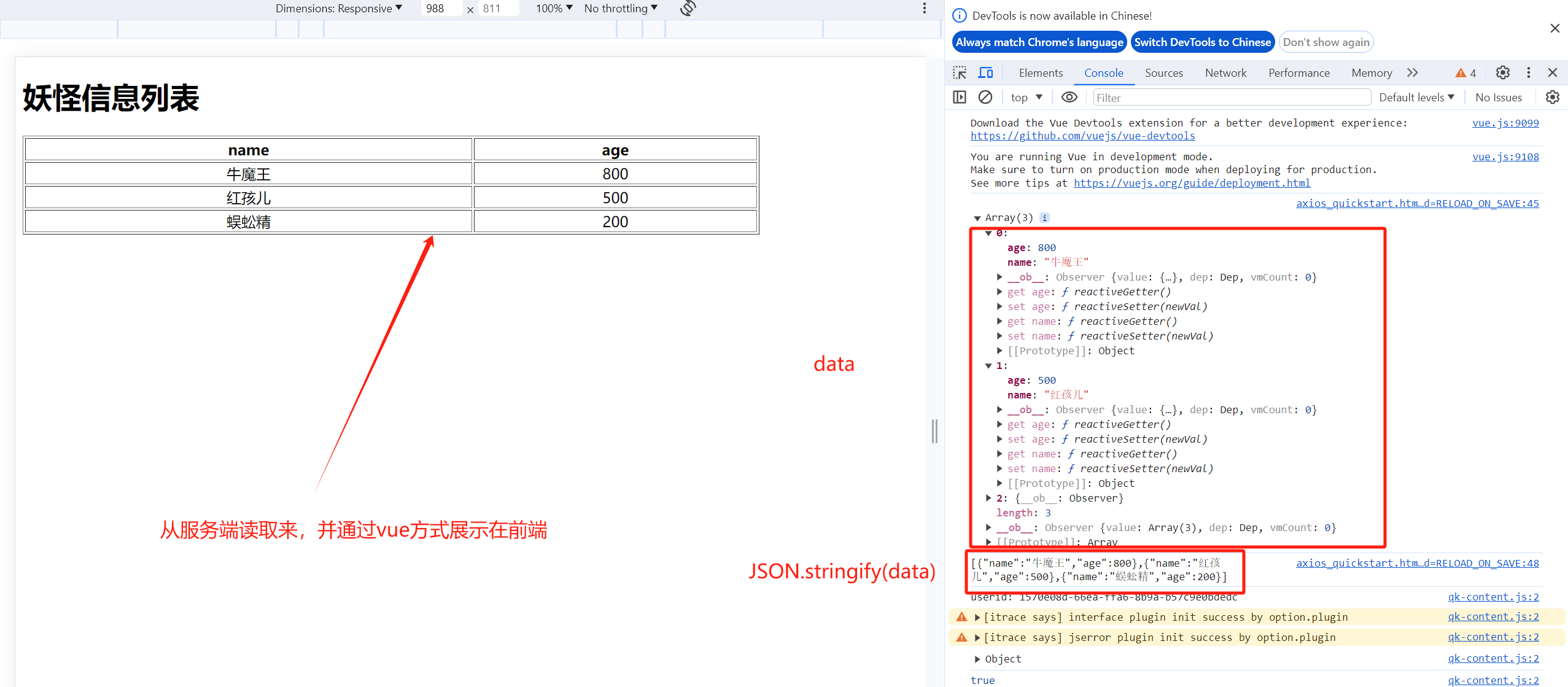
Vue Axios——前端技术栈
文章目录 基本介绍Vue是什么? MVVMVue的使用快速入门注意事项和使用细节 Vue 数据绑定机制分析数据单向渲染注意事项和细节 双向数据绑定事件绑定示例:注意事项和使用细节课后作业1课后作业2 修饰符示例 条件渲染/控制: v-if v-showv-if VS v-show课后作…...
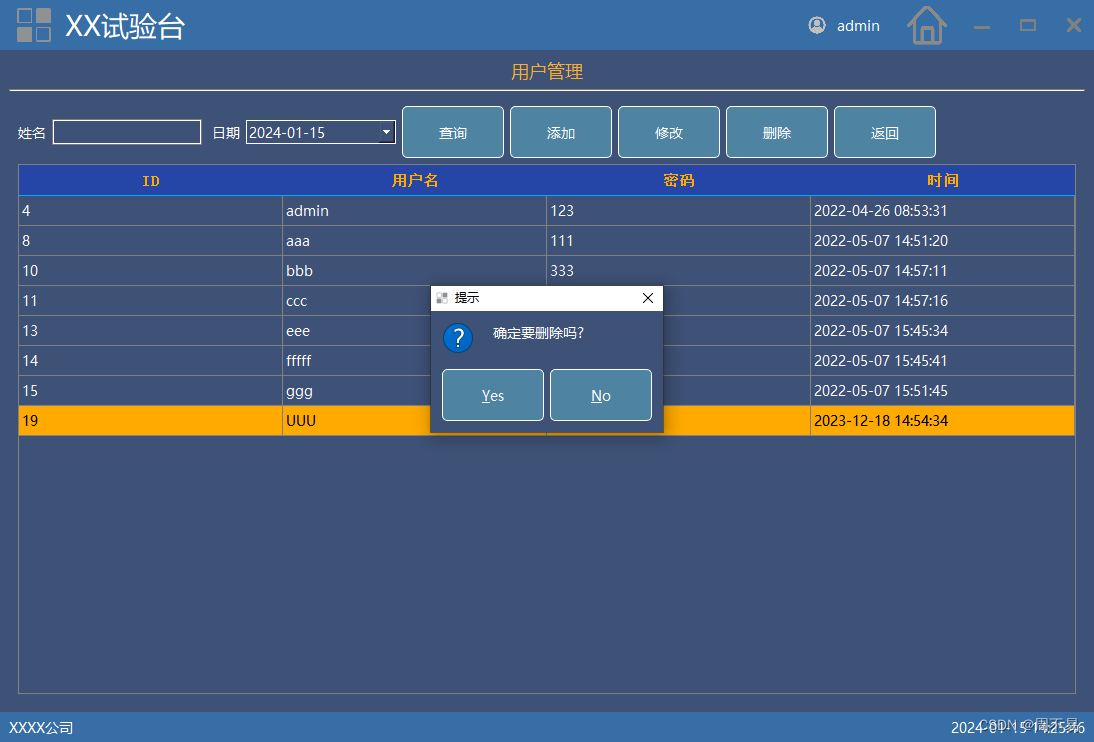
九、Qt C++ 数据库开发
《一、QT的前世今生》 《二、QT下载、安装及问题解决(windows系统)》《三、Qt Creator使用》 《四、Qt 的第一个demo-CSDN博客》 《五、带登录窗体的demo》 《六、新建窗体时,几种窗体的区别》 《七、Qt 信号和槽》 《八、Qt C 毕业设计》 《九、Qt …...

力扣电话号码的组合
文章目录 题目说明做题思路代码实现代码解析 题目链接 题目说明 首先我们先分析一下这个题目题目中说呢先给出一个字符串这个字符串其实就是这个九键数字我们要按照要求将数字所代表的字符进行自由组合形成一个字符串并且这个字符串的长度和输入的数字字符串长度相同࿰…...

ZooKeeper 实战(五) Curator实现分布式锁
文章目录 ZooKeeper 实战(五) Curator实现分布式锁1.简介1.1.分布式锁概念1.2.Curator 分布式锁的实现方式1.3.分布式锁接口 2.准备工作3.分布式可重入锁3.1.锁对象3.2.非重入式抢占锁测试代码输出日志 3.3.重入式抢占锁测试代码输出日志 4.分布式非可重入锁4.1.锁对象4.2.重入…...

基于kubernetes部署MySQL主从环境
部署方式 通过部署mysql主从容器,配置主从pod之间数据同步。 配置数据库访问的密码 创建 Mysql 密码的 Secret [rootk8s-master1 master]# kubectl create secret generic mysql-password --namespaceapp --from-literalmysql_root_passwordroot secret/mysql-pas…...

网络编程(Modbus进阶)
思维导图 Modbus RTU(先学一点理论) 概念 Modbus RTU 是工业自动化领域 最广泛应用的串行通信协议,由 Modicon 公司(现施耐德电气)于 1979 年推出。它以 高效率、强健性、易实现的特点成为工业控制系统的通信标准。 包…...

XCTF-web-easyupload
试了试php,php7,pht,phtml等,都没有用 尝试.user.ini 抓包修改将.user.ini修改为jpg图片 在上传一个123.jpg 用蚁剑连接,得到flag...

Spark 之 入门讲解详细版(1)
1、简介 1.1 Spark简介 Spark是加州大学伯克利分校AMP实验室(Algorithms, Machines, and People Lab)开发通用内存并行计算框架。Spark在2013年6月进入Apache成为孵化项目,8个月后成为Apache顶级项目,速度之快足见过人之处&…...

【人工智能】神经网络的优化器optimizer(二):Adagrad自适应学习率优化器
一.自适应梯度算法Adagrad概述 Adagrad(Adaptive Gradient Algorithm)是一种自适应学习率的优化算法,由Duchi等人在2011年提出。其核心思想是针对不同参数自动调整学习率,适合处理稀疏数据和不同参数梯度差异较大的场景。Adagrad通…...

基于Flask实现的医疗保险欺诈识别监测模型
基于Flask实现的医疗保险欺诈识别监测模型 项目截图 项目简介 社会医疗保险是国家通过立法形式强制实施,由雇主和个人按一定比例缴纳保险费,建立社会医疗保险基金,支付雇员医疗费用的一种医疗保险制度, 它是促进社会文明和进步的…...

《用户共鸣指数(E)驱动品牌大模型种草:如何抢占大模型搜索结果情感高地》
在注意力分散、内容高度同质化的时代,情感连接已成为品牌破圈的关键通道。我们在服务大量品牌客户的过程中发现,消费者对内容的“有感”程度,正日益成为影响品牌传播效率与转化率的核心变量。在生成式AI驱动的内容生成与推荐环境中࿰…...

Spring Boot+Neo4j知识图谱实战:3步搭建智能关系网络!
一、引言 在数据驱动的背景下,知识图谱凭借其高效的信息组织能力,正逐步成为各行业应用的关键技术。本文聚焦 Spring Boot与Neo4j图数据库的技术结合,探讨知识图谱开发的实现细节,帮助读者掌握该技术栈在实际项目中的落地方法。 …...

MySQL中【正则表达式】用法
MySQL 中正则表达式通过 REGEXP 或 RLIKE 操作符实现(两者等价),用于在 WHERE 子句中进行复杂的字符串模式匹配。以下是核心用法和示例: 一、基础语法 SELECT column_name FROM table_name WHERE column_name REGEXP pattern; …...

dify打造数据可视化图表
一、概述 在日常工作和学习中,我们经常需要和数据打交道。无论是分析报告、项目展示,还是简单的数据洞察,一个清晰直观的图表,往往能胜过千言万语。 一款能让数据可视化变得超级简单的 MCP Server,由蚂蚁集团 AntV 团队…...

Device Mapper 机制
Device Mapper 机制详解 Device Mapper(简称 DM)是 Linux 内核中的一套通用块设备映射框架,为 LVM、加密磁盘、RAID 等提供底层支持。本文将详细介绍 Device Mapper 的原理、实现、内核配置、常用工具、操作测试流程,并配以详细的…...
