303. 区域和检索 - 数组不可变
303. 区域和检索 - 数组不可变
给定一个整数数组 nums,处理以下类型的多个查询:
计算索引 left 和 right (包含 left 和 right)之间的 nums 元素的 和 ,其中 left <= right
实现 NumArray 类:
- NumArray(int[] nums) 使用数组 nums 初始化对象
- int sumRange(int i, int j) 返回数组 nums 中索引 left 和 right 之间的元素的 总和 ,包含 left 和 right 两点(也就是 nums[left] + nums[left + 1] + … + nums[right] )
示例 1:
输入:
["NumArray", "sumRange", "sumRange", "sumRange"]
[[[-2, 0, 3, -5, 2, -1]], [0, 2], [2, 5], [0, 5]]
输出:
[null, 1, -1, -3]解释:
NumArray numArray = new NumArray([-2, 0, 3, -5, 2, -1]);
numArray.sumRange(0, 2); // return 1 ((-2) + 0 + 3)
numArray.sumRange(2, 5); // return -1 (3 + (-5) + 2 + (-1))
numArray.sumRange(0, 5); // return -3 ((-2) + 0 + 3 + (-5) + 2 + (-1))
提示:
- 1<=nums.length<=1041 <= nums.length <= 10^41<=nums.length<=104
- −105<=nums[i]<=105-10^5 <= nums[i] <= 10^5−105<=nums[i]<=105
- 0<=i<=j<nums.length0 <= i <= j < nums.length0<=i<=j<nums.length
- 最多调用 10410^4104 次 sumRange 方法
思路:(前缀和)
根据数学层面可以这样理解:

代码理解: 前缀和数组 sums[i]里面存的就是原数组num的前 i 项和,例如sums[2] 这里面存的就是原数组num的前2项和
而数组最大的优点就是便于可以直接根据索引查找,前缀和就是充分运用了数组这个优点,只要理解了前缀和这个概念,代码的思路其实很简单 思路:
1、首先创建一个前缀和数组int []sums
2、由于前缀和数组sums[]里面存的是原数组num的前i项和,故使用其构造方法创建前缀数组sums[]时,要引入原数组num[]
3、注意创建sums[]数组时要注意,数组长度比数组要大一个数组空间,方便数组查询
4、创建完毕后,就直接根据传过来的right和left来对前缀和数组进行查找,注意查找right时注意加一,防止数组下标越界 , 5、查找到之后,再让两个查找到的数进行相减
6、相减之后的数就返回其值
代码:(Java)
public class NumArray {public int[] sums;public NumArray(int[] nums) {sums = new int[nums.length + 1];sums[0] = 0;for(int i = 1; i <= nums.length ; i++) {sums[i] = sums[i - 1] + nums[i - 1];}}public int sumRange(int left, int right) {return sums[right+1] - sums[left];}}
public class Demo {public static void main(String[] args) {// TODO Auto-generated method stubint numbers [][] = {{-2, 0, 3, -5, 2, -1}, {0, 2}, {2, 5}, {0, 5}};int sums[] = new int[numbers.length - 1];NumArray numary = new NumArray(numbers[0]);for(int i = 1; i < numbers.length; i++) {sums[i-1] = numary.sumRange(numbers[i][0], numbers[i][1]);System.out.print(sums[i - 1] + " ");} }
}
复杂度分析:
-
时间复杂度:初始化 O(n),每次检索 O(1),其中 n 是数组 nums的长度。 初始化需要遍历数组 nums 计算前缀和,时间复杂度是 O(n)。 每次检索只需要得到两个下标处的前缀和,然后计算差值,时间复杂度是 O(1)。
-
空间复杂度:O(n),其中 n 是数组 nums 的长度。需要创建一个长度为 n+1的前缀和数组。
注:仅供学习参考!
题目来源:力扣。
相关文章:

303. 区域和检索 - 数组不可变
303. 区域和检索 - 数组不可变 给定一个整数数组 nums,处理以下类型的多个查询: 计算索引 left 和 right (包含 left 和 right)之间的 nums 元素的 和 ,其中 left < right 实现 NumArray 类: NumArray(int[] num…...

Spring Cloud融合Nacos配置加载优先级 | Spring Cloud 8
一、前言 Spring Cloud Alibaba Nacos Config 目前提供了三种配置能力从 Nacos 拉取相关的配置: A:通过内部相关规则(应用名、扩展名、profiles)自动生成相关的 Data Id 配置B:通过 spring.cloud.nacos.config.extension-configs的方式支持…...
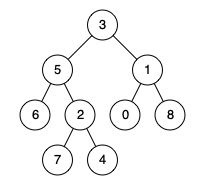
LeetCode 236.二叉树的最近公共祖先
给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。百度百科中最近公共祖先的定义为:“对于有根树 T 的两个节点 p、q,最近公共祖先表示为一个节点 x,满足 x 是 p、q 的祖先且 x 的深度尽可能大(一个节点也可以是它自己的祖…...
)
awk简单实例(持续更新中)
一 概述 awk命令是一种分析和处理文本文件的编程工具。它的功能非常强大,是Linux/Unix系统中最常用的过滤工具。 awk内建变量: NF 整个数据行(即$0)拥有的字段总数 NR 当前awk所处理的数据行的编号 $0 当前awk所处理的数据行 $1 数据行的第1个字段 $2 数…...
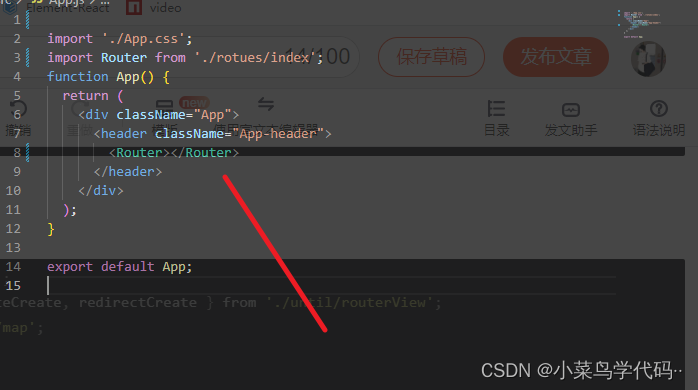
react动态路由组件的封装
react动态路由组件的封装 我这篇比较全面 首先下载包 npm i react-router-dom5 这里为什么要用5的版本为啥不用最新的,原因在于老版本跟新版本写法不一样 老版本 import { HashRouter, Route, Switch, Redirect } from react-router-dom;render() {return (<Ha…...
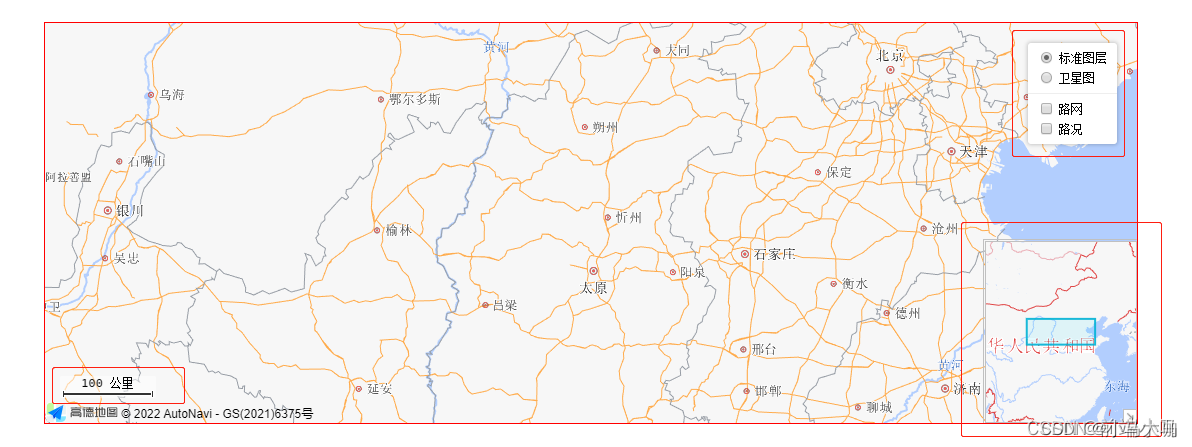
Vue项目中引入高德地图步骤详解
高德地图API官网:高德开放平台 | 高德地图API。 目录 一、案例效果 二、开发准备 1. 注册高德开放平台账号 2. 创建应用添加 key 值 三、项目中使用地图组件 1. npm 获取高德地图 API 2.在项目中新建 MapContainer.vue 文件,用作地图组件。 3.在…...

软件测试用例篇(2)
功能测试界面测试兼容性测试安全测试易用性测试性能测试 针对有需求的案例来设计测试用例:邮箱注册,部分测试用例 https://zay1xofb7z6.feishu.cn/mindnotes/bmncnKD5Ak6GSZl3PRlWDgF9z3g#mindmap 一)等价类: 场景需求:姓名长度是6-200位,那么如何进行设…...

leetcode题解-27. Remove Element
给你一个数组 nums 和一个值 val,你需要 原地 移除所有数值等于 val 的元素,并返回移除后数组的新长度。 不要使用额外的数组空间,你必须仅使用 O(1) 额外空间并 原地 修改输入数组。 元素的顺序可以改变。你不需要考虑数组中超出新长度后面…...
【fly-iot飞凡物联】(4):在linux系统上搭建arduino环境,可以使用离线包,导入到arduino上即可。
目录前言1,关于2,然后就可以找到ESP32,ESP8266的主版3,方法2,github下载,然后手动添加到ide中吧4,总结前言 本文的原文连接是: https://blog.csdn.net/freewebsys/article/details/108971807 未…...

java实例解析类图中【关联、组合和聚合】的区别
总目录链接==>> AutoSAR入门和实战系列总目录 文章目录 聚合Composition聚合与组合的区别关联是两个独立类之间的关系,它通过它们的对象建立关联。关联可以是一对一、一对多、多对一、多对多。在面向对象的编程中,一个对象与另一个对象通信以使用该对象提供的功能和服…...

基于m-p条件查询代码生成
目录 起因 演示 使用 0.自定义注解 1.定义一个dto的条件查询类 2.调用主程序 效果图 小结 代码 注解 Dto类 完整代码 起因 最近两天一直写后台管理统计的增删改查(很少写增删改查,所以不是很熟练),几乎每个表都要涉及到条件查询的业务…...
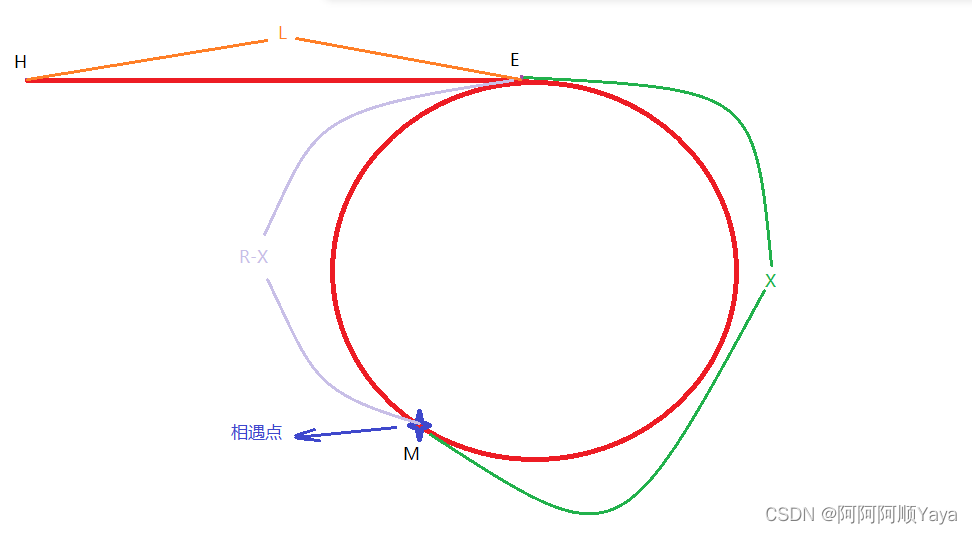
【LeetCode】带环链表两道题
第一题:环形链表 问题介绍 给你一个链表的头节点head ,判断链表中是否有环。 如果链表中有某个节点,可以通过连续跟踪next指针再次到达,则链表中存在环。为了表示给定链表中的环,评测系统内部使用整数pos 来表示链表…...
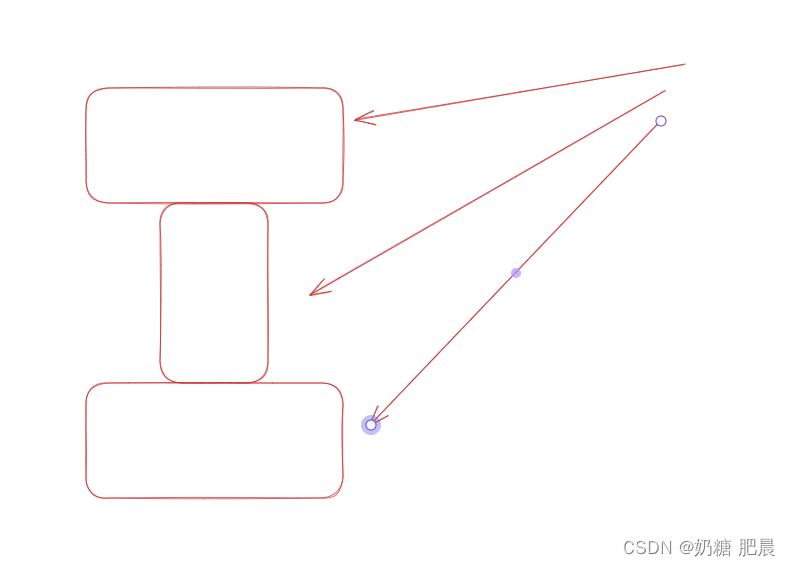
CSS奇思妙想之-利用CSS裁剪(clip-path)完成各种图形
在日常开发当中,如果想要开发多边形,一般都需要多个盒子或者伪元素的帮助,有没有一直办法能只使用一个盒子实现呢? 有的:css裁剪 clip-path介绍 css裁剪(clip-path)这个属性平时率非常低。但是…...

力扣每日一题刷题总结:哈希表篇
剑指 Offer II 033.变位词组 Medium 哈希表 变位词 2023/3/3 给定一个字符串数组 strs ,将 变位词 组合在一起。 可以按任意顺序返回结果列表。 注意:若两个字符串中每个字符出现的次数都相同,则称它们互为变位词。 示例: 示例 1:…...
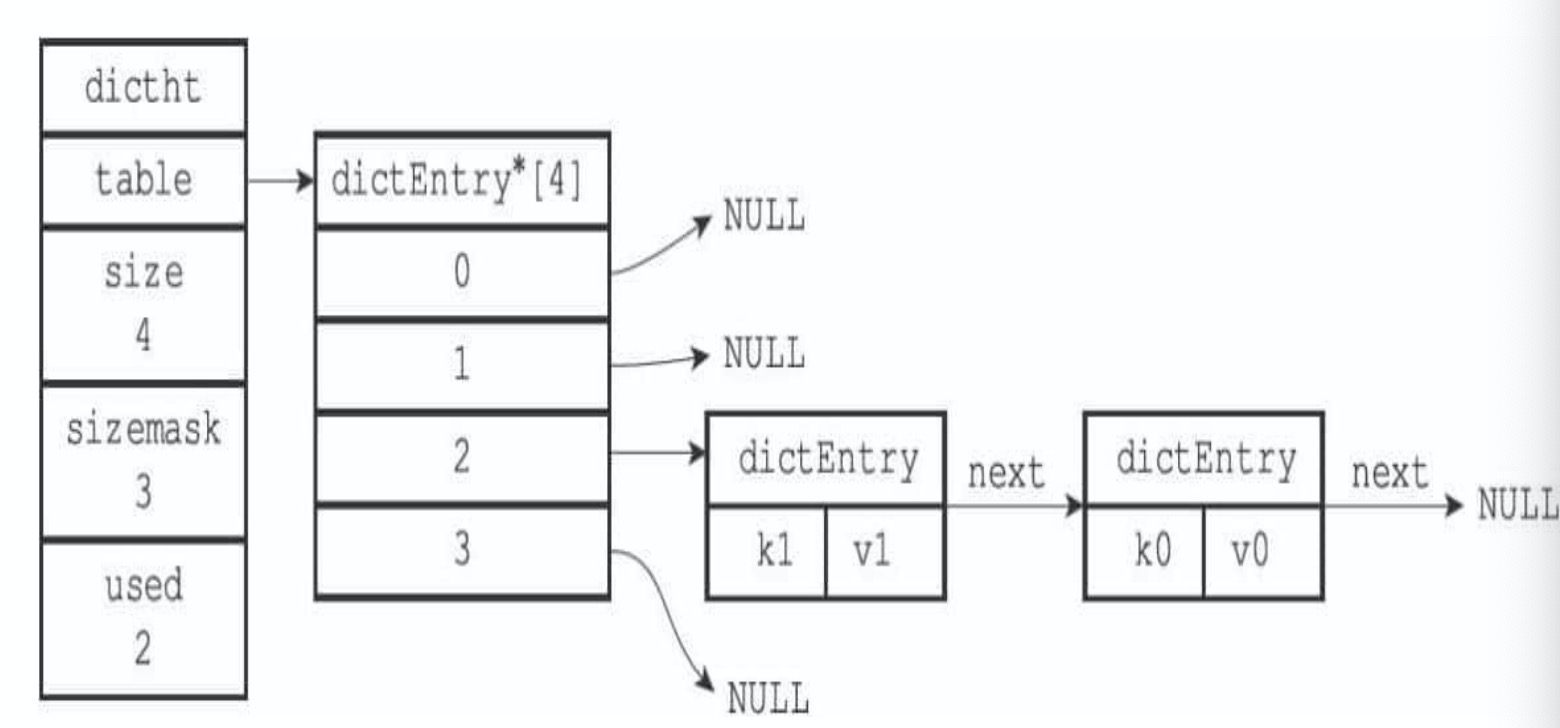
【Redis】redis大key和大value的危害,如何处理?
前序 还记得上次和同事一起去面试候选人时,同事提了一个问题:Redis的大key有什么危害?当时候选人主要作答的角度是一个key的value较大时的情况,比如: 内存不均:单value较大时,可能会导致节点之…...

Spring Boot:实现MyBatis动态创建表
在有些应用场景中,我们会有需要动态创建和操作表的需求。 比如因为单表数据存储量太大而采取分表存储的情况,又或者是按日期生成日志表存储系统日志等等。这个时候就需要我们动态的生成和操作数据库表了。 而我们都知道,以往我们使用MyBati…...

SpringBoot+Seata在多数据源和feign中的简单使用
SpringBootSeata简单使用 目录seata执行过程安装seata下载seata使用自定义配置文件,NACOS为注册中心结合springboot实现AT模式1.多数据源引入依赖bootstrap.yml配置在使用的方法上用GlobalTransactional注解调用接口正常时调用接口报错时回滚2.配合feignseata优缺点seata执行过…...
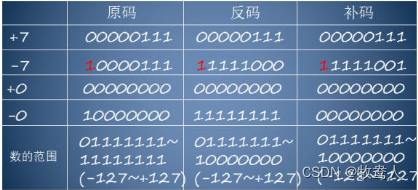
计算机网络中的原码、反码、补码
写在前面 原码、反码、补码是计算机组成原理中的概念,是计算机网络的基础知识之一。这些概念是为了处理二进制数的符号位而引入的,常用于计算机中的整数运算,也常用于数据存储和传输等领域。因此,了解和掌握这些概念对于理解计算机…...

七、Bean的实例化方式
Spring为Bean提供了多种实例化方式,通常包括4种方式。(也就是说在Spring中为Bean对象的创建准备了多种方案,目的是:更加灵活) 第一种:通过构造方法实例化第二种:通过简单工厂模式实例化第三种&…...
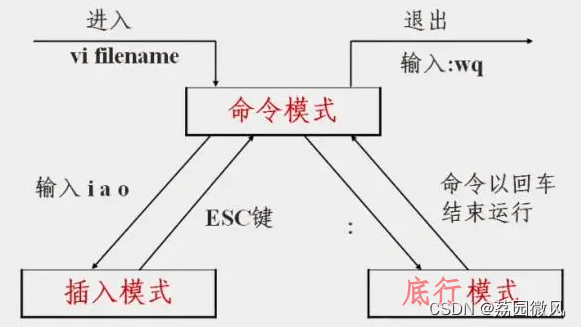
Windows程序员学习Linux环境下VI(VIM)编辑器的使用方法
我是荔园微风,作为一名在IT界整整25年的老兵,今天我们来重新审视一下Windows程序员如何学习Linux环境知识。由于很多程序在Windows环境下开发好后,还要部署到Linux服务器上去,所以作为Windows程序员有必要学习Linux环境的知识。VI…...

idea大量爆红问题解决
问题描述 在学习和工作中,idea是程序员不可缺少的一个工具,但是突然在有些时候就会出现大量爆红的问题,发现无法跳转,无论是关机重启或者是替换root都无法解决 就是如上所展示的问题,但是程序依然可以启动。 问题解决…...

零门槛NAS搭建:WinNAS如何让普通电脑秒变私有云?
一、核心优势:专为Windows用户设计的极简NAS WinNAS由深圳耘想存储科技开发,是一款收费低廉但功能全面的Windows NAS工具,主打“无学习成本部署” 。与其他NAS软件相比,其优势在于: 无需硬件改造:将任意W…...

Unity3D中Gfx.WaitForPresent优化方案
前言 在Unity中,Gfx.WaitForPresent占用CPU过高通常表示主线程在等待GPU完成渲染(即CPU被阻塞),这表明存在GPU瓶颈或垂直同步/帧率设置问题。以下是系统的优化方案: 对惹,这里有一个游戏开发交流小组&…...

前端开发面试题总结-JavaScript篇(一)
文章目录 JavaScript高频问答一、作用域与闭包1.什么是闭包(Closure)?闭包有什么应用场景和潜在问题?2.解释 JavaScript 的作用域链(Scope Chain) 二、原型与继承3.原型链是什么?如何实现继承&a…...

CMake 从 GitHub 下载第三方库并使用
有时我们希望直接使用 GitHub 上的开源库,而不想手动下载、编译和安装。 可以利用 CMake 提供的 FetchContent 模块来实现自动下载、构建和链接第三方库。 FetchContent 命令官方文档✅ 示例代码 我们将以 fmt 这个流行的格式化库为例,演示如何: 使用 FetchContent 从 GitH…...

网络编程(UDP编程)
思维导图 UDP基础编程(单播) 1.流程图 服务器:短信的接收方 创建套接字 (socket)-----------------------------------------》有手机指定网络信息-----------------------------------------------》有号码绑定套接字 (bind)--------------…...

Android 之 kotlin 语言学习笔记三(Kotlin-Java 互操作)
参考官方文档:https://developer.android.google.cn/kotlin/interop?hlzh-cn 一、Java(供 Kotlin 使用) 1、不得使用硬关键字 不要使用 Kotlin 的任何硬关键字作为方法的名称 或字段。允许使用 Kotlin 的软关键字、修饰符关键字和特殊标识…...

【数据分析】R版IntelliGenes用于生物标志物发现的可解释机器学习
禁止商业或二改转载,仅供自学使用,侵权必究,如需截取部分内容请后台联系作者! 文章目录 介绍流程步骤1. 输入数据2. 特征选择3. 模型训练4. I-Genes 评分计算5. 输出结果 IntelliGenesR 安装包1. 特征选择2. 模型训练和评估3. I-Genes 评分计…...

人工智能(大型语言模型 LLMs)对不同学科的影响以及由此产生的新学习方式
今天是关于AI如何在教学中增强学生的学习体验,我把重要信息标红了。人文学科的价值被低估了 ⬇️ 转型与必要性 人工智能正在深刻地改变教育,这并非炒作,而是已经发生的巨大变革。教育机构和教育者不能忽视它,试图简单地禁止学生使…...
集成 Mybatis-Plus 和 Mybatis-Plus-Join)
纯 Java 项目(非 SpringBoot)集成 Mybatis-Plus 和 Mybatis-Plus-Join
纯 Java 项目(非 SpringBoot)集成 Mybatis-Plus 和 Mybatis-Plus-Join 1、依赖1.1、依赖版本1.2、pom.xml 2、代码2.1、SqlSession 构造器2.2、MybatisPlus代码生成器2.3、获取 config.yml 配置2.3.1、config.yml2.3.2、项目配置类 2.4、ftl 模板2.4.1、…...
