【LeetCode】带环链表两道题
第一题:环形链表
问题介绍
给你一个链表的头节点head ,判断链表中是否有环。
如果链表中有某个节点,可以通过连续跟踪next指针再次到达,则链表中存在环。为了表示给定链表中的环,评测系统内部使用整数pos 来表示链表尾连接到链表中的位置(索引从 0 开始)。注意:pos不作为参数进行传递 。仅仅是为了标识链表的实际情况。
如果链表中存在环 ,则返回true。 否则,返回false 。
问题设置:
- 链表中节点的数目范围是
[0, 10^4] -10^5 <= Node.val <= 10^5pos为-1或者链表中的一个有效索引。
问题解释:
问题的函数接口传过来的是不带哨兵位的单链表。
可以使用快慢指针来解决。先让快指针和慢指针都指向链表的起始结点,快指针一次走两步,慢指针一次走一步。
如果是带环链表,快指针先进环,慢指针后进环,就成了追及问题。
如果不是带环链表,快指针会走到空,此时结束。
一些问题分析
-
那为什么快指针一次走两步,慢指针一次走一步,快指针就一定能在环内追上慢指针,和慢指针相遇呢?
当快慢指针都进环后,
最好的情况是,慢指针一进环,就和快指针相遇,程序就结束。
最坏的情况是,慢指针一进环,快指针在慢指针的前一个位置。
假设环内的结点数为N,此时快指针和慢指针相差了N-1步,
因为快指针一次走两步,慢指针一次走一步,每次快指针都比慢指针多走一步,(N-1)的差值会不断减1,直到减为0。
所以慢指针走N-1步后,快指针就会追上慢指针和慢指针相遇。
可以发现:在慢指针进环后,快指针一定可以在慢指针走完一圈之前追上慢指针和慢指针相遇。 -
那为什么一定是快指针一次走两步,慢指针一次走一步才行,快指针一次走三步,走四步等等不行吗?
首先快指针一次走的步数如果大于两步,循环结束的判断条件会更不好控制是一方面;
同时,像上一个问题分析的,如果慢指针进环后,快指针和慢指针的差距步是N-1,
当快指针一次走三步,慢指针一次走一步,快指针和慢指针每走一次,差距步就缩减两步。
如果N是奇数的情况下,N-1是偶数,(N-1)不断以两步的速度缩减,最终会减为0,也就是快指针追上慢指针和慢指针相遇了
但如果N是偶数的情况下,N-1是奇数,(N-1)不断以两步的速度缩减(也就是:N-1,N-3,…,3,1,-1);差距步并不能减为0,也就是快指针能追上慢指针,但会和慢指针擦肩而过,直到差距步减为-1的情况出现,快指针又恰好处于慢指针的前一个位置,差距步又恢复为N-1,这就导致在某些极端场景下,出现快指针永远追不上慢指针的问题。
快指针一次走四步等情况,也是类似的道理,就不再赘述。
如果你非要抬杠说,让快指针一次走三步,慢指针一次走两步,进环后差距步也是每次缩减1步,快指针最后也会追上慢指针并和慢指针相遇,不是吗?
那我只能说:对对对,你说得对!
参考代码
bool hasCycle(struct ListNode* head)
{struct ListNode* slow=head;struct ListNode* fast=head;//因为fast一次走两步,所以需要同时判断fast和fast->next是不是NULLwhile(fast!=NULL&&fast->next!=NULL){slow=slow->next;fast=fast->next->next;if(slow==fast){return true;}}return false;
}
第二题:环形链表 II
问题介绍
给定一个链表的头节点head,返回链表开始入环的第一个节点。如果链表无环,则返回null。
如果链表中有某个节点,可以通过连续跟踪next指针再次到达,则链表中存在环。为了表示给定链表中的环,评测系统内部使用整数pos来表示链表尾连接到链表中的位置(索引从 0 开始)。如果pos是-1,则在该链表中没有环。注意:pos不作为参数进行传递,仅仅是为了标识链表的实际情况。
不允许修改链表。
问题设置
链表中节点的数目范围在范围[0, 10^4]内
-10\^5 <= Node.val <= 10\^5
pos的值为-1或者链表中的一个有效索引
问题解释
这道题相较上一道题,需要返回带环链表的入环结点。
问题的函数接口传过来的也是不带哨兵位的单链表。
解决这道题需要画图和进行简单的数学分析
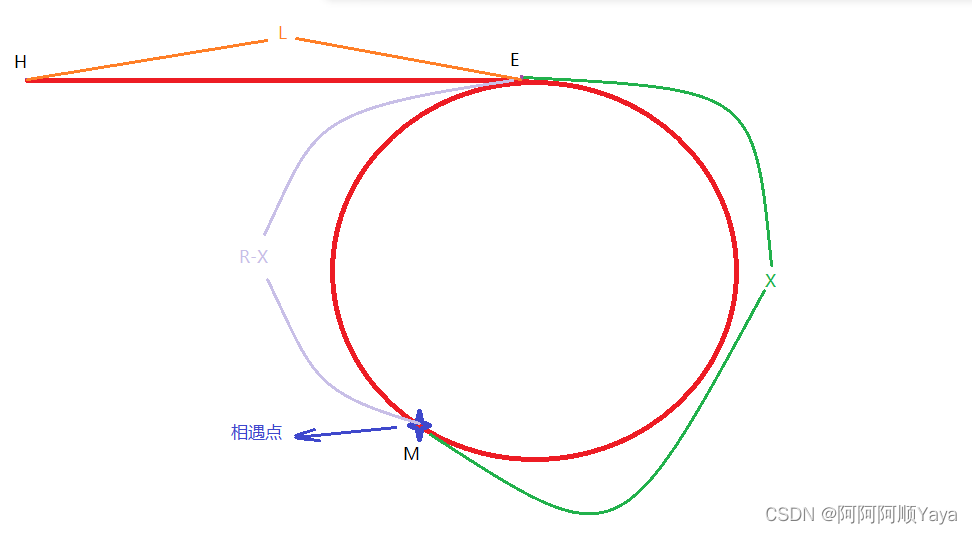
假设H为链表的起始点,E为入口点,M为相遇点,
H到E的距离为L,环的大小为R,E到M的距离为X,则M到E的距离为R-X
当快指针和慢指针在M点相遇时,
慢指针走过的距离是:L+X;
快指针走过的距离是:L+n*R+X(n>=1);
在第一题中已经分析:
最好的情况是,慢指针一进环,就和快指针相遇,程序就结束,
此时对于快指针来说,n恰好是1;
最坏的情况是,慢指针一进环,快指针在慢指针的前一个位置,
此时慢指针需要走N-1步,快指针自然要走2倍的N-1步,快指针如果想追上慢指针,就必须先到达入口点E,最终n也可以说是大于等于1的。
但是,这样说未免有失偏颇。
当L很短,而R很大的时候,上述情况可能还说得过;
但如果L很长,R很小,在慢指针还未入环的时候,快指针已经在环内跑了好几圈,这就是另一种情况了。
所以可得出n是大于等于1的。
有了上述的铺垫,可以列出数学等式:
2(L+X) = L+nR+X
=> L+X = nR = (n-1)*R+R
=> L= (n-1)R+R-X
这说明什么呢?
也就是说,有两个指针,一个从H点出发,一个从M点出发,当他们相遇时,他们共同所指的结点就是带环链表的入环结点。
是不是很神奇,下面用代码验证一下吧。
参考代码
struct ListNode* detectCycle(struct ListNode* head)
{struct ListNode* slow=head;struct ListNode* fast=head;while(fast!=NULL&&fast->next!=NULL){slow=slow->next;fast=fast->next->next;//找到相遇点if(slow==fast){struct ListNode* cur1=head;struct ListNode* cur2=slow;while(cur1!=cur2){cur1=cur1->next;cur2=cur2->next;}return cur1;}}return NULL;
}
相关文章:

【LeetCode】带环链表两道题
第一题:环形链表 问题介绍 给你一个链表的头节点head ,判断链表中是否有环。 如果链表中有某个节点,可以通过连续跟踪next指针再次到达,则链表中存在环。为了表示给定链表中的环,评测系统内部使用整数pos 来表示链表…...
CSS奇思妙想之-利用CSS裁剪(clip-path)完成各种图形
在日常开发当中,如果想要开发多边形,一般都需要多个盒子或者伪元素的帮助,有没有一直办法能只使用一个盒子实现呢? 有的:css裁剪 clip-path介绍 css裁剪(clip-path)这个属性平时率非常低。但是…...

力扣每日一题刷题总结:哈希表篇
剑指 Offer II 033.变位词组 Medium 哈希表 变位词 2023/3/3 给定一个字符串数组 strs ,将 变位词 组合在一起。 可以按任意顺序返回结果列表。 注意:若两个字符串中每个字符出现的次数都相同,则称它们互为变位词。 示例: 示例 1:…...
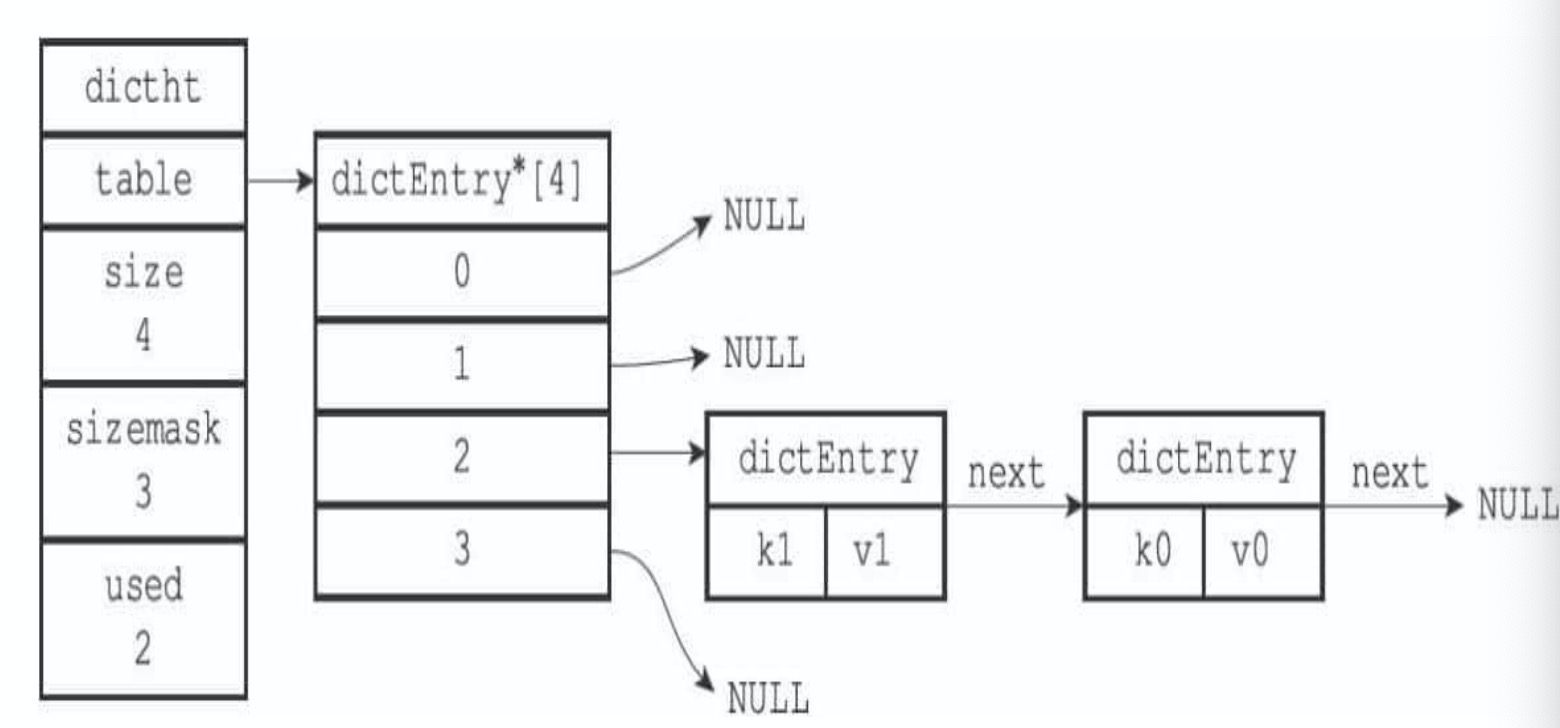
【Redis】redis大key和大value的危害,如何处理?
前序 还记得上次和同事一起去面试候选人时,同事提了一个问题:Redis的大key有什么危害?当时候选人主要作答的角度是一个key的value较大时的情况,比如: 内存不均:单value较大时,可能会导致节点之…...

Spring Boot:实现MyBatis动态创建表
在有些应用场景中,我们会有需要动态创建和操作表的需求。 比如因为单表数据存储量太大而采取分表存储的情况,又或者是按日期生成日志表存储系统日志等等。这个时候就需要我们动态的生成和操作数据库表了。 而我们都知道,以往我们使用MyBati…...

SpringBoot+Seata在多数据源和feign中的简单使用
SpringBootSeata简单使用 目录seata执行过程安装seata下载seata使用自定义配置文件,NACOS为注册中心结合springboot实现AT模式1.多数据源引入依赖bootstrap.yml配置在使用的方法上用GlobalTransactional注解调用接口正常时调用接口报错时回滚2.配合feignseata优缺点seata执行过…...
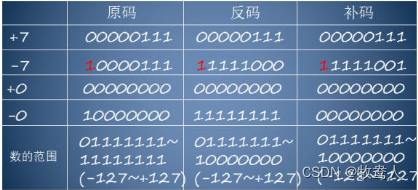
计算机网络中的原码、反码、补码
写在前面 原码、反码、补码是计算机组成原理中的概念,是计算机网络的基础知识之一。这些概念是为了处理二进制数的符号位而引入的,常用于计算机中的整数运算,也常用于数据存储和传输等领域。因此,了解和掌握这些概念对于理解计算机…...

七、Bean的实例化方式
Spring为Bean提供了多种实例化方式,通常包括4种方式。(也就是说在Spring中为Bean对象的创建准备了多种方案,目的是:更加灵活) 第一种:通过构造方法实例化第二种:通过简单工厂模式实例化第三种&…...
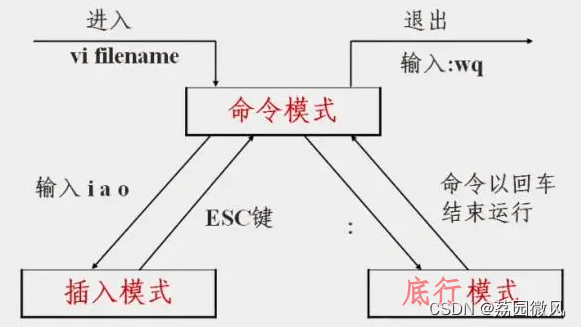
Windows程序员学习Linux环境下VI(VIM)编辑器的使用方法
我是荔园微风,作为一名在IT界整整25年的老兵,今天我们来重新审视一下Windows程序员如何学习Linux环境知识。由于很多程序在Windows环境下开发好后,还要部署到Linux服务器上去,所以作为Windows程序员有必要学习Linux环境的知识。VI…...

react入门篇
react入门篇前言一、目标二、项目环境三、实现过程(干货满满💥💥💥)1.创建react项目2.arco design UI库3.路由模块化4. 状态管理zustand5. axios6. 路由守卫前言 提示:这里可以添加本文要记录的大概内容&a…...

阿赵的MaxScript学习笔记分享九《可编辑多面体的操作》
大家好,我是阿赵。这是MaxScript学习笔记分享的第九篇,可编辑多面体的操作。不知不觉写了这么多篇了,应该还有几篇就写完了。自己给自己加一下油。 在3DsMax里面如果需要建模,一般使用到的塌陷方式有3种,可编辑的网格、…...
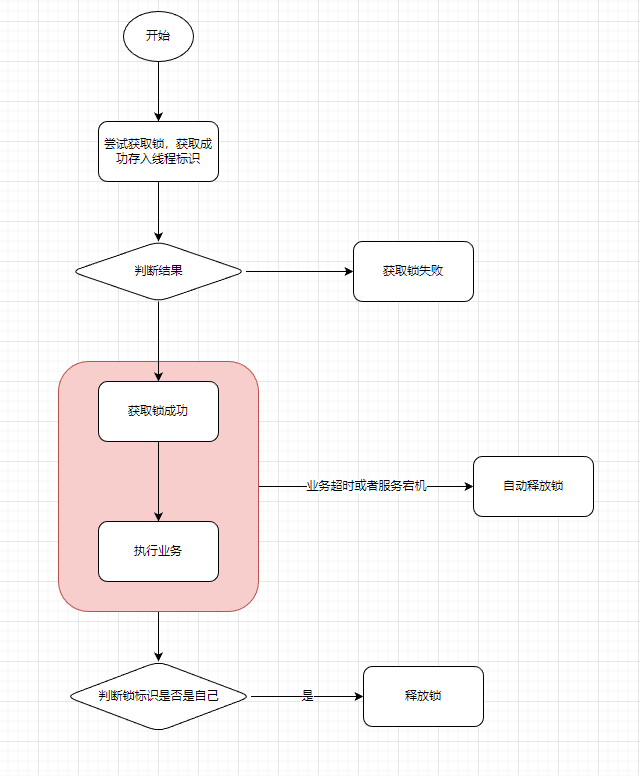
【Redis场景5】集群秒杀优化-分布式锁
集群环境下的秒杀问题 前序 【Redis场景1】用户登录注册 【Redis场景2】缓存更新策略(双写一致) 【Redis场景3】缓存穿透、击穿问题 【Redis场景拓展】秒杀问题-全局唯一ID生成策略 【Redis场景4】单机环境下秒杀问题 在单机环境下的并发问题,我们可以使用相关…...
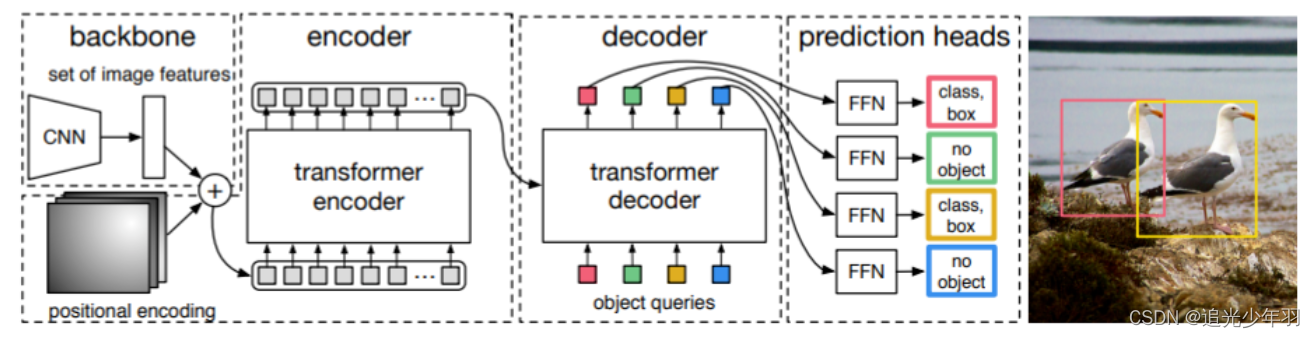
transformer目标检测开山之作detr
1. 将一个batch的图片输入backone获得feature。 (2,c,w,h)先输入resnet50中,得到(2,2048,w,h)。虽然这里channel不是256,但是在输入e…...
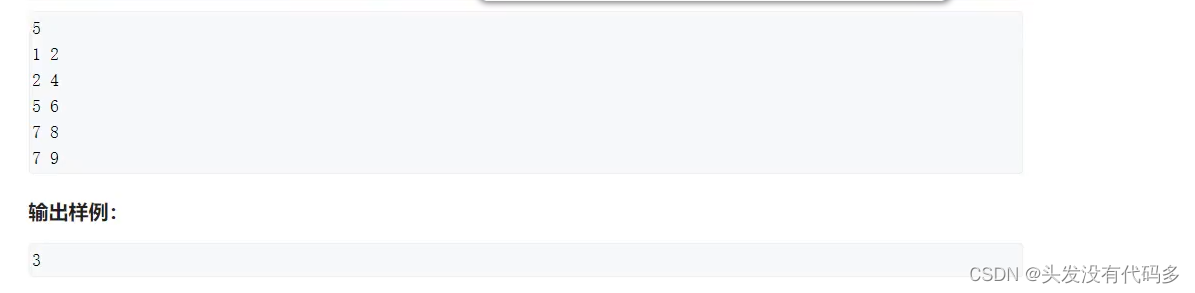
双指针法|位运算|离散化|区间合并
目录 双指针算法 位运算 离散化 序列合并 双指针算法 题目描述:1.输入n个单词,每个单词在输入的时候按空格隔开,之后打印出每个单词且换行 #include<iostream> #include <string>using namespace std; int main() {strin…...
Rockchip Android13 GKI开发指南
Rockchip Android13 GKI开发指南 文章目录Rockchip Android13 GKI开发指南GKI介绍Google upstream kernel下载及编译Rockchip SDK中GKI相关目录介绍Rockchip GKI编译代码修改编译固件烧写KO编译及修改添加新的模块驱动的方法调试ko方法开机log确认uboot阶段Android阶段KO加载KO…...

手把手教你原生JavaScript打造丝滑流畅的轮播图,让你的网站瞬间提升用户体验!
简介 轮播图是网页设计中常见的交互组件之一,用于展示多张图片或内容,让用户能够方便地浏览、切换和选择。本文将介绍如何使用原生 JavaScript 手写一个简单的轮播图,并且通过代码解释实现细节。 目录 简介 HTML 结构 CSS 样式 JavaScr…...

git常用基本操作
克隆远程代码更新本地代码 git clone <-b | -branch> [branch name] [repository URL] git pull #拉取远程仓库代码,更新本地仓库 git merge <branch-name> #合并目标分支 建立本地仓库分支 git branch #查看当…...

剑指 Offer —— 数组和字符串
文章目录剑指 Offer 04. 二维数组中的查找代码实现解题方案 思路算法步骤剑指 Offer 05. 替换空格题目描述代码实现解题方案 思路算法步骤剑指 Offer 11. 旋转数组的最小数字 - 解决方案题目描述剑指 Offer 04. 二维数组中的查找 在一个 n * m 的二维数组中: 每…...
Java 字符编码
编码:数据存储进计算机中需要转换为二进制存储,这个过程就是编码。 解码:计算机读取数据并展示在页面上,需要将二进制转换为人类语言的过程,叫做解码。 乱码:如果编码和解码时使用的码表不一样,…...
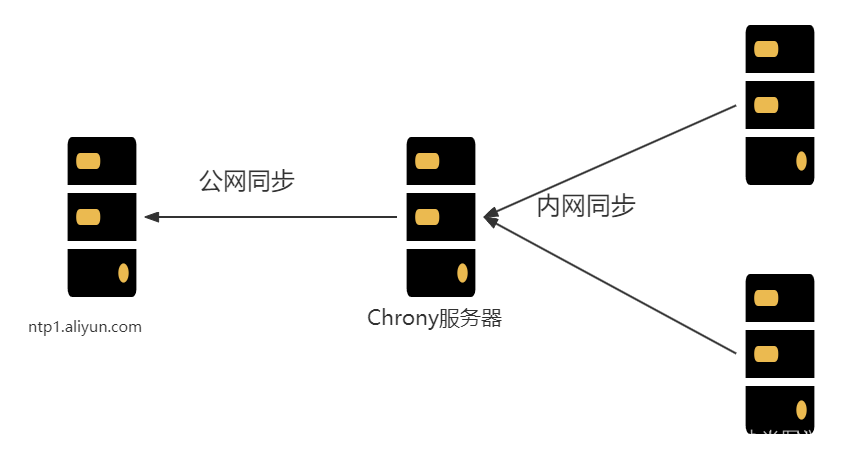
ubuntu-9-安装chrony时间同步
使用chrony搭建时间同步服务器 [Linux系列]Chrony时间同步服务器 配置chrony服务,实现服务器时间自动同步 linux上内网环境配置NTP时间同步详解 经验体会:解决Ubuntu 18.04Windows双系统时间不同步的问题 1 时间同步 我们知道一台电脑主机,…...

基于大模型的 UI 自动化系统
基于大模型的 UI 自动化系统 下面是一个完整的 Python 系统,利用大模型实现智能 UI 自动化,结合计算机视觉和自然语言处理技术,实现"看屏操作"的能力。 系统架构设计 #mermaid-svg-2gn2GRvh5WCP2ktF {font-family:"trebuchet ms",verdana,arial,sans-…...
)
椭圆曲线密码学(ECC)
一、ECC算法概述 椭圆曲线密码学(Elliptic Curve Cryptography)是基于椭圆曲线数学理论的公钥密码系统,由Neal Koblitz和Victor Miller在1985年独立提出。相比RSA,ECC在相同安全强度下密钥更短(256位ECC ≈ 3072位RSA…...

23-Oracle 23 ai 区块链表(Blockchain Table)
小伙伴有没有在金融强合规的领域中遇见,必须要保持数据不可变,管理员都无法修改和留痕的要求。比如医疗的电子病历中,影像检查检验结果不可篡改行的,药品追溯过程中数据只可插入无法删除的特性需求;登录日志、修改日志…...

Day131 | 灵神 | 回溯算法 | 子集型 子集
Day131 | 灵神 | 回溯算法 | 子集型 子集 78.子集 78. 子集 - 力扣(LeetCode) 思路: 笔者写过很多次这道题了,不想写题解了,大家看灵神讲解吧 回溯算法套路①子集型回溯【基础算法精讲 14】_哔哩哔哩_bilibili 完…...

STM32标准库-DMA直接存储器存取
文章目录 一、DMA1.1简介1.2存储器映像1.3DMA框图1.4DMA基本结构1.5DMA请求1.6数据宽度与对齐1.7数据转运DMA1.8ADC扫描模式DMA 二、数据转运DMA2.1接线图2.2代码2.3相关API 一、DMA 1.1简介 DMA(Direct Memory Access)直接存储器存取 DMA可以提供外设…...

Python爬虫(一):爬虫伪装
一、网站防爬机制概述 在当今互联网环境中,具有一定规模或盈利性质的网站几乎都实施了各种防爬措施。这些措施主要分为两大类: 身份验证机制:直接将未经授权的爬虫阻挡在外反爬技术体系:通过各种技术手段增加爬虫获取数据的难度…...

C/C++ 中附加包含目录、附加库目录与附加依赖项详解
在 C/C 编程的编译和链接过程中,附加包含目录、附加库目录和附加依赖项是三个至关重要的设置,它们相互配合,确保程序能够正确引用外部资源并顺利构建。虽然在学习过程中,这些概念容易让人混淆,但深入理解它们的作用和联…...

如何更改默认 Crontab 编辑器 ?
在 Linux 领域中,crontab 是您可能经常遇到的一个术语。这个实用程序在类 unix 操作系统上可用,用于调度在预定义时间和间隔自动执行的任务。这对管理员和高级用户非常有益,允许他们自动执行各种系统任务。 编辑 Crontab 文件通常使用文本编…...
详细解析)
Caliper 负载(Workload)详细解析
Caliper 负载(Workload)详细解析 负载(Workload)是 Caliper 性能测试的核心部分,它定义了测试期间要执行的具体合约调用行为和交易模式。下面我将全面深入地讲解负载的各个方面。 一、负载模块基本结构 一个典型的负载模块(如 workload.js)包含以下基本结构: use strict;/…...

苹果AI眼镜:从“工具”到“社交姿态”的范式革命——重新定义AI交互入口的未来机会
在2025年的AI硬件浪潮中,苹果AI眼镜(Apple Glasses)正在引发一场关于“人机交互形态”的深度思考。它并非简单地替代AirPods或Apple Watch,而是开辟了一个全新的、日常可接受的AI入口。其核心价值不在于功能的堆叠,而在于如何通过形态设计打破社交壁垒,成为用户“全天佩戴…...
