FLoyd算法的入门与应用
目录
一、前言
二、FLoyd算法
1、最短路问题
2、Floyd算法
3、Floyd的特点
4、Floyd算法思想:动态规划
三、例题
1、蓝桥公园(lanqiaoOJ题号1121)
2、路径(2021年初赛 lanqiaoOJ题号1460)
一、前言
本文主要讲了最短路问题,以及解决最短路问题的Floyd算法概念与两道简单的相关例题。
二、FLoyd算法
1、最短路问题
- 最广为人知的图论问题。
- 简单图的最短路径
① 树上的路径:任意2点之间只有一条路径
② 所有边长都为 1 的图:用 BFS 搜最短路径,复杂度O(n+m)
- 普通图的最短路径
① 边长:不一定等于 1,而且可能为负数
② 算法:Floyd、Dijkstra、SPFA 等,各有应用场景,不可互相替代
【最短路算法比较】

2、Floyd算法
- 最简单的最短路径算法,代码仅有5行
- 存图:最简单的矩阵存图
- 易懂,比暴力的搜索更简单易懂
- 效率不高,不能用于大图
- 在某些场景下有自己的优势,难以替代。
def Floyd():for k in range(1,n+1):for i in range(1,n+1):for j in range(1,n+1):if dp[i][k]+dp[k][j]<dp[i][j]:dp[i][j]=dp[i][k]+dp[k][j]3、Floyd的特点
- Floyd算法:“多源” 最短路算法,一次计算能得到图中每一对结点之间 (多对多) 的最短路径。
- Dijkstra、 Bellman-Ford、 SPFA算法:"单源” 最短路径算法 (Single sourceshortest path algorithm),一次计算能得到一个起点到其他所有点 (一对多) 的最短路径。
- 在截止目前的蓝桥杯大赛中,Floyd算法是最常见的最短路径算法。
4、Floyd算法思想:动态规划
动态规划:求图上两点 i、j 之间的最短距离,按 “从小图到全图” 的步骤,在逐步扩大图的过程中计算和更新最短路。
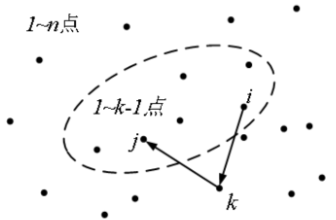
定义状态:dp[k][i][j],i、j、k 是点的编号,范围 1~n。状态 dp[k][i][j] 表示在包含 1~k 点的子图上,点对 i、j 之间的最短路。
状态转移方程:从子图 1~k-1 扩展到子图 1~k
dp[k][i][j] = min(dp[k-1][i][j], dp[k-1][i][k] +dp[k-1][k][j])
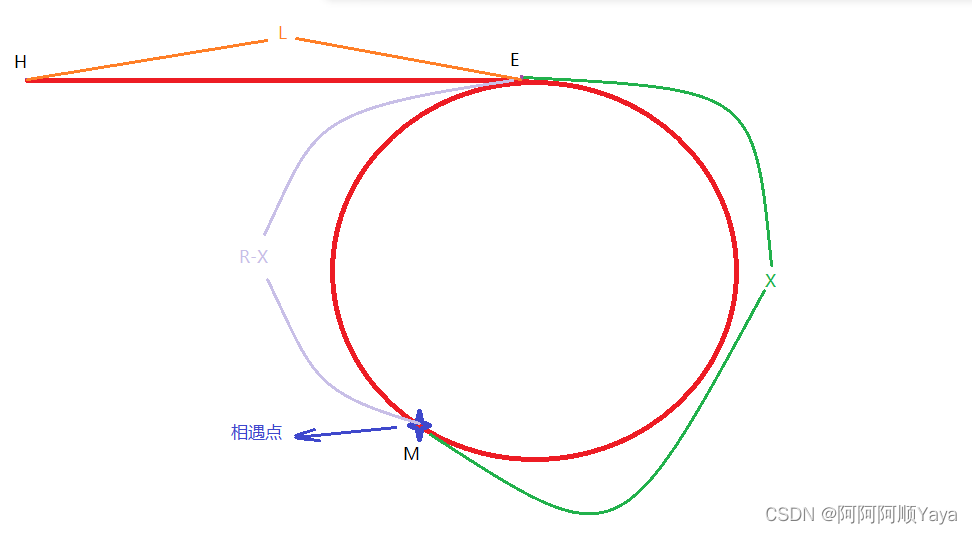
- 虚线圆圈:包含1~k-1点的子图。
- dp[k-1][i][j]:虚线子图内的点对 i、j 的最短路;
- dp[k-1][i][k]+dp[k-1][k][j]:经过 k 点的新路径的长度,即这条路径从 i 出发,先到 k,再从 k 到终点 j。
- 比较:不经过 k 的最短路径 dp[k-1][i][j] 和经过 k 的新路径,较小者就是新的 dp[k][i][j]。
- k 从 1 逐步扩展到 n:最后得到的 dp[n][i][j] 是点对 i、j 之间的最短路径长度。
- 初值 dp[0][i][j]:若 i、j 是直连的,就是它们的边长;若不直连,赋值为无穷大。
- i、j 是任意点对:计算结束后得到了所有点对之间的最短路。
【方程的简化】(这里留个眼)
dp[k][i][j] = min(dp[k-1][i][j], dp[k-1][i][k]+dp[k-1][k][j])
用滚动数组简化:
dp[i][j]=min(dp[i][j], dp[i][k] + dp[k][j])
【Floyd算法总结】
- 1)在一次计算后求得所有结点之间的最短距离。
- 2)代码极其简单,是最简单的最短路算法。
- 3)效率低下,计算复杂度是 O(n^3),只能用于 n <300 的小规模的图。
- 4)存图用邻接矩阵 dp[][] 。因为 Floyd 算法计算的结果是所有点对之间的最短路,本身就需要 n^2 的空间,用矩阵存储最合适。
- 5)能判断负圈。负圈:若图中有权值为负的边,某个经过这个负边的环路,所有边长相加的总长度也是负数,这就是负圈。在这个负圈上每绕一圈,总长度就更小,从而陷入在负圈上兜圈子的死循环。
- Floyd算法很容易判断负圈,只要在算法运行过程出现任意一个 dp[i][j]<0 就说明有负圈。因为 dp[i][j] 是从 i 出发,经过其他中转点绕一圈回到自己的最短路径,如果小于零,就存在负圈。
三、例题
1、蓝桥公园(lanqiaoOJ题号1121)
【题目描述】
小明来到了蓝桥公园。已知公园有 N 个景点,景点和景点之间一共有 M 条道路。小明有 Q 个观景计划,每个计划包含一个起点 st 和一个终点 ed,表示他想从 st 去到 ed。但是小明的体力有限,对于每个计划他想走最少的路完成,你可以帮帮他吗?
【输入描述】
输入第一行包含三个正整数 N, M, Q。第 2 到 M+1 行每行包含三个正整数 u, v, w,表示 u、v 之间存在一条距离为 w 的路。第 M+2 到 M+Q-1 行每行包含两个正整数 st, ed,其含义如题所述。
1<=N<=400, 1<=M<=N*(N-1)/2, Q<=10^3, 1<=u, v, st, ed<=n, 1<=w<=10^9
【输出描述】
输出共 Q 行,对应输入数据中的查询。若无法从 st 到达 ed 则输出 -1。
def floyd():global mpglobal Nglobal Mglobal Qfor k in range(1,N+1):for i in range(1,N+1):for j in range(1,N+1):mp[i][j]=min(mp[i][j],mp[i][k]+mp[k][j])N,M,Q=map(int,input().split())
mp=[[1100000000]*(M+2) for _ in range(N+2)]
for _ in range(M):u,v,w=map(int,input().split())w=min(mp[u][v],w) #考虑重边,选最小权值那条mp[u][v]=wmp[v][u]=w
floyd()
for _ in range(Q):st,ed=map(int,input().split())if mp[st][ed]==1100000000: #st无法到达edprint(-1)elif st==ed: #有可能兜一圈回到起点呢,所以要特判print(0)else:print(mp[st][ed])2、路径(2021年初赛 lanqiaoOJ题号1460)
填空题
【题目描述】
小蓝的图由 2021 个结点组成,依次编号1至2021。对于两个不同的结点 a, b,如果 a 和 b 的差的绝对值大于 21,则两个结点之间没有边相连;如果 a 和 b 的差的绝对值小于等于 21,则两个点之间有一条长度为 a 和 b 的最小公倍数的无向边相连。例如:结点 1 和结点 23 之间没有边相连;结点 3 和结点 24 之间有一条无向边,长度为 24;结点 15 和结点 25 之间有一条无向边,长度为75。
请计算,结点 1 和结点 2021 之间的最短路径长度是多少。
【常规的floyd】:运行时间长达30分钟!
from math import *
def lcm(x,y):return x//gcd(x,y)*y #求最小公倍数
dp=[[int(0x3f3f3f3f3f3f3f3f) for _ in range(2022)] for _ in range(2022)]def floyd():global dpfor k in range(1,2022):for i in range(1,2022):for j in range(1,2022):dp[i][j]=min(dp[i][j],dp[i][k]+dp[k][j])for i in range(1,2022):for j in range(1,2022):if abs(i-j)<=21:dp[i][j]=lcm(i,j)
floyd()
print(dp[1][2021])
【简化版floyd】
from math import *
def lcm(x,y):return x//gcd(x,y)*y #求最小公倍数
dp=[[int(0x3f3f3f3f3f3f3f3f) for _ in range(2022)] for _ in range(2022)]def floyd():global dpfor k in range(1,2022):#for i in range(1,2022):for i in range(1,2):for j in range(1,2022):dp[i][j]=min(dp[i][j],dp[i][k]+dp[k][j])for i in range(1,2022):for j in range(1,2022):if abs(i-j)<=21:dp[i][j]=lcm(i,j)
floyd()
print(dp[1][2021])
我们只求点 1 到其他点的最短路就行!这实际上这变成了 Bellman-ford 算法。
【Bellman-ford更简洁的写法】
from math import *
def lcm(x,y):return x//gcd(x,y)*y #求最小公倍数
dp=[int(0x3f3f3f3f3f3f3f3f)]*2022 #dp[i]:点i到点1的最短路径
d[1]=0
for i in range(1,2022): #点ifor j in range(i+1,i+22): #和i有边的点jif j>2021:breakdp[j]=min(dp[j],dp[i]+lcm(i,j)) #更新最短路
print(dp[2021])
以上,FLoyd算法的入门与应用
祝好
相关文章:
FLoyd算法的入门与应用
目录 一、前言 二、FLoyd算法 1、最短路问题 2、Floyd算法 3、Floyd的特点 4、Floyd算法思想:动态规划 三、例题 1、蓝桥公园(lanqiaoOJ题号1121) 2、路径(2021年初赛 lanqiaoOJ题号1460) 一、前言 本文主要…...

303. 区域和检索 - 数组不可变
303. 区域和检索 - 数组不可变 给定一个整数数组 nums,处理以下类型的多个查询: 计算索引 left 和 right (包含 left 和 right)之间的 nums 元素的 和 ,其中 left < right 实现 NumArray 类: NumArray(int[] num…...

Spring Cloud融合Nacos配置加载优先级 | Spring Cloud 8
一、前言 Spring Cloud Alibaba Nacos Config 目前提供了三种配置能力从 Nacos 拉取相关的配置: A:通过内部相关规则(应用名、扩展名、profiles)自动生成相关的 Data Id 配置B:通过 spring.cloud.nacos.config.extension-configs的方式支持…...
LeetCode 236.二叉树的最近公共祖先
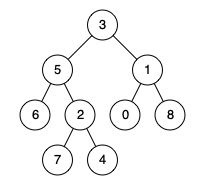
给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。百度百科中最近公共祖先的定义为:“对于有根树 T 的两个节点 p、q,最近公共祖先表示为一个节点 x,满足 x 是 p、q 的祖先且 x 的深度尽可能大(一个节点也可以是它自己的祖…...
)
awk简单实例(持续更新中)
一 概述 awk命令是一种分析和处理文本文件的编程工具。它的功能非常强大,是Linux/Unix系统中最常用的过滤工具。 awk内建变量: NF 整个数据行(即$0)拥有的字段总数 NR 当前awk所处理的数据行的编号 $0 当前awk所处理的数据行 $1 数据行的第1个字段 $2 数…...
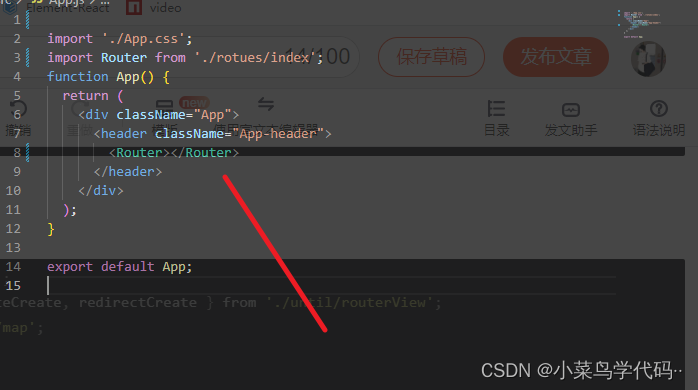
react动态路由组件的封装
react动态路由组件的封装 我这篇比较全面 首先下载包 npm i react-router-dom5 这里为什么要用5的版本为啥不用最新的,原因在于老版本跟新版本写法不一样 老版本 import { HashRouter, Route, Switch, Redirect } from react-router-dom;render() {return (<Ha…...
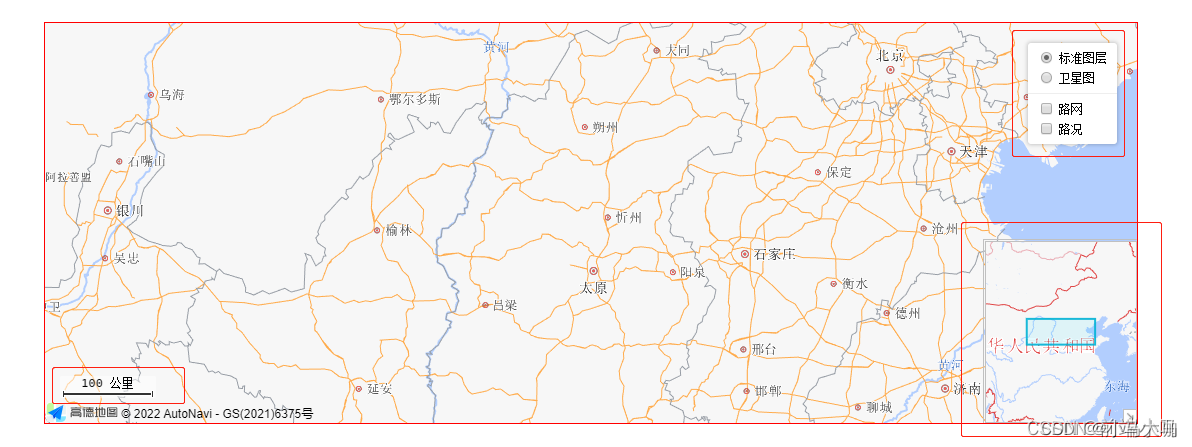
Vue项目中引入高德地图步骤详解
高德地图API官网:高德开放平台 | 高德地图API。 目录 一、案例效果 二、开发准备 1. 注册高德开放平台账号 2. 创建应用添加 key 值 三、项目中使用地图组件 1. npm 获取高德地图 API 2.在项目中新建 MapContainer.vue 文件,用作地图组件。 3.在…...

软件测试用例篇(2)
功能测试界面测试兼容性测试安全测试易用性测试性能测试 针对有需求的案例来设计测试用例:邮箱注册,部分测试用例 https://zay1xofb7z6.feishu.cn/mindnotes/bmncnKD5Ak6GSZl3PRlWDgF9z3g#mindmap 一)等价类: 场景需求:姓名长度是6-200位,那么如何进行设…...

leetcode题解-27. Remove Element
给你一个数组 nums 和一个值 val,你需要 原地 移除所有数值等于 val 的元素,并返回移除后数组的新长度。 不要使用额外的数组空间,你必须仅使用 O(1) 额外空间并 原地 修改输入数组。 元素的顺序可以改变。你不需要考虑数组中超出新长度后面…...
【fly-iot飞凡物联】(4):在linux系统上搭建arduino环境,可以使用离线包,导入到arduino上即可。
目录前言1,关于2,然后就可以找到ESP32,ESP8266的主版3,方法2,github下载,然后手动添加到ide中吧4,总结前言 本文的原文连接是: https://blog.csdn.net/freewebsys/article/details/108971807 未…...

java实例解析类图中【关联、组合和聚合】的区别
总目录链接==>> AutoSAR入门和实战系列总目录 文章目录 聚合Composition聚合与组合的区别关联是两个独立类之间的关系,它通过它们的对象建立关联。关联可以是一对一、一对多、多对一、多对多。在面向对象的编程中,一个对象与另一个对象通信以使用该对象提供的功能和服…...

基于m-p条件查询代码生成
目录 起因 演示 使用 0.自定义注解 1.定义一个dto的条件查询类 2.调用主程序 效果图 小结 代码 注解 Dto类 完整代码 起因 最近两天一直写后台管理统计的增删改查(很少写增删改查,所以不是很熟练),几乎每个表都要涉及到条件查询的业务…...
【LeetCode】带环链表两道题
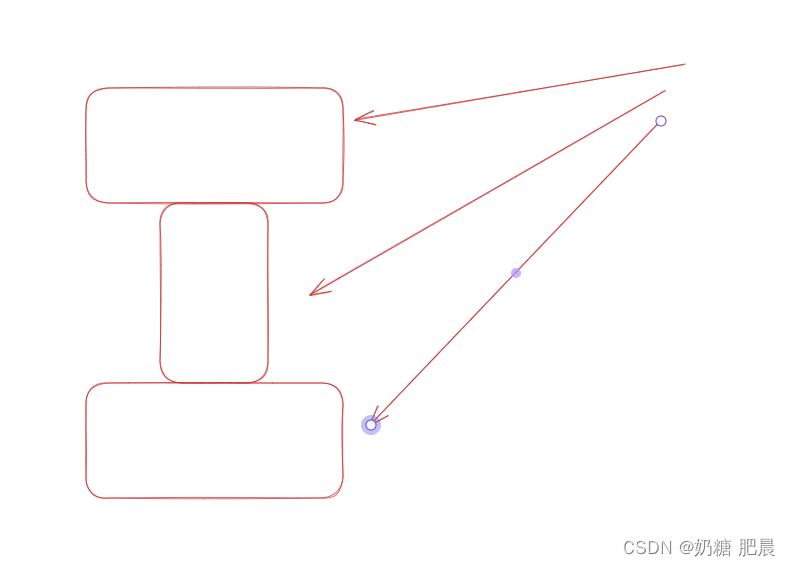
第一题:环形链表 问题介绍 给你一个链表的头节点head ,判断链表中是否有环。 如果链表中有某个节点,可以通过连续跟踪next指针再次到达,则链表中存在环。为了表示给定链表中的环,评测系统内部使用整数pos 来表示链表…...
CSS奇思妙想之-利用CSS裁剪(clip-path)完成各种图形
在日常开发当中,如果想要开发多边形,一般都需要多个盒子或者伪元素的帮助,有没有一直办法能只使用一个盒子实现呢? 有的:css裁剪 clip-path介绍 css裁剪(clip-path)这个属性平时率非常低。但是…...

力扣每日一题刷题总结:哈希表篇
剑指 Offer II 033.变位词组 Medium 哈希表 变位词 2023/3/3 给定一个字符串数组 strs ,将 变位词 组合在一起。 可以按任意顺序返回结果列表。 注意:若两个字符串中每个字符出现的次数都相同,则称它们互为变位词。 示例: 示例 1:…...
【Redis】redis大key和大value的危害,如何处理?
前序 还记得上次和同事一起去面试候选人时,同事提了一个问题:Redis的大key有什么危害?当时候选人主要作答的角度是一个key的value较大时的情况,比如: 内存不均:单value较大时,可能会导致节点之…...

Spring Boot:实现MyBatis动态创建表
在有些应用场景中,我们会有需要动态创建和操作表的需求。 比如因为单表数据存储量太大而采取分表存储的情况,又或者是按日期生成日志表存储系统日志等等。这个时候就需要我们动态的生成和操作数据库表了。 而我们都知道,以往我们使用MyBati…...

SpringBoot+Seata在多数据源和feign中的简单使用
SpringBootSeata简单使用 目录seata执行过程安装seata下载seata使用自定义配置文件,NACOS为注册中心结合springboot实现AT模式1.多数据源引入依赖bootstrap.yml配置在使用的方法上用GlobalTransactional注解调用接口正常时调用接口报错时回滚2.配合feignseata优缺点seata执行过…...
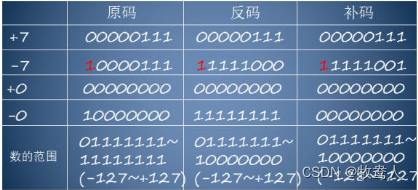
计算机网络中的原码、反码、补码
写在前面 原码、反码、补码是计算机组成原理中的概念,是计算机网络的基础知识之一。这些概念是为了处理二进制数的符号位而引入的,常用于计算机中的整数运算,也常用于数据存储和传输等领域。因此,了解和掌握这些概念对于理解计算机…...

七、Bean的实例化方式
Spring为Bean提供了多种实例化方式,通常包括4种方式。(也就是说在Spring中为Bean对象的创建准备了多种方案,目的是:更加灵活) 第一种:通过构造方法实例化第二种:通过简单工厂模式实例化第三种&…...

[2025CVPR]DeepVideo-R1:基于难度感知回归GRPO的视频强化微调框架详解
突破视频大语言模型推理瓶颈,在多个视频基准上实现SOTA性能 一、核心问题与创新亮点 1.1 GRPO在视频任务中的两大挑战 安全措施依赖问题 GRPO使用min和clip函数限制策略更新幅度,导致: 梯度抑制:当新旧策略差异过大时梯度消失收敛困难:策略无法充分优化# 传统GRPO的梯…...

ES6从入门到精通:前言
ES6简介 ES6(ECMAScript 2015)是JavaScript语言的重大更新,引入了许多新特性,包括语法糖、新数据类型、模块化支持等,显著提升了开发效率和代码可维护性。 核心知识点概览 变量声明 let 和 const 取代 var…...

使用分级同态加密防御梯度泄漏
抽象 联邦学习 (FL) 支持跨分布式客户端进行协作模型训练,而无需共享原始数据,这使其成为在互联和自动驾驶汽车 (CAV) 等领域保护隐私的机器学习的一种很有前途的方法。然而,最近的研究表明&…...

智能在线客服平台:数字化时代企业连接用户的 AI 中枢
随着互联网技术的飞速发展,消费者期望能够随时随地与企业进行交流。在线客服平台作为连接企业与客户的重要桥梁,不仅优化了客户体验,还提升了企业的服务效率和市场竞争力。本文将探讨在线客服平台的重要性、技术进展、实际应用,并…...

EtherNet/IP转DeviceNet协议网关详解
一,设备主要功能 疆鸿智能JH-DVN-EIP本产品是自主研发的一款EtherNet/IP从站功能的通讯网关。该产品主要功能是连接DeviceNet总线和EtherNet/IP网络,本网关连接到EtherNet/IP总线中做为从站使用,连接到DeviceNet总线中做为从站使用。 在自动…...

IoT/HCIP实验-3/LiteOS操作系统内核实验(任务、内存、信号量、CMSIS..)
文章目录 概述HelloWorld 工程C/C配置编译器主配置Makefile脚本烧录器主配置运行结果程序调用栈 任务管理实验实验结果osal 系统适配层osal_task_create 其他实验实验源码内存管理实验互斥锁实验信号量实验 CMISIS接口实验还是得JlINKCMSIS 简介LiteOS->CMSIS任务间消息交互…...

全面解析各类VPN技术:GRE、IPsec、L2TP、SSL与MPLS VPN对比
目录 引言 VPN技术概述 GRE VPN 3.1 GRE封装结构 3.2 GRE的应用场景 GRE over IPsec 4.1 GRE over IPsec封装结构 4.2 为什么使用GRE over IPsec? IPsec VPN 5.1 IPsec传输模式(Transport Mode) 5.2 IPsec隧道模式(Tunne…...

2025季度云服务器排行榜
在全球云服务器市场,各厂商的排名和地位并非一成不变,而是由其独特的优势、战略布局和市场适应性共同决定的。以下是根据2025年市场趋势,对主要云服务器厂商在排行榜中占据重要位置的原因和优势进行深度分析: 一、全球“三巨头”…...

脑机新手指南(七):OpenBCI_GUI:从环境搭建到数据可视化(上)
一、OpenBCI_GUI 项目概述 (一)项目背景与目标 OpenBCI 是一个开源的脑电信号采集硬件平台,其配套的 OpenBCI_GUI 则是专为该硬件设计的图形化界面工具。对于研究人员、开发者和学生而言,首次接触 OpenBCI 设备时,往…...

毫米波雷达基础理论(3D+4D)
3D、4D毫米波雷达基础知识及厂商选型 PreView : https://mp.weixin.qq.com/s/bQkju4r6med7I3TBGJI_bQ 1. FMCW毫米波雷达基础知识 主要参考博文: 一文入门汽车毫米波雷达基本原理 :https://mp.weixin.qq.com/s/_EN7A5lKcz2Eh8dLnjE19w 毫米波雷达基础…...
