B - Build Roads (最小生成树 + 打表)
https://vjudge.net/problem/Gym-103118B/origin

在猫的国度里,有n个城市。猫国国王想要修n -1条路来连接所有的城市。第i市有一家ai经验价值的建筑公司。要在第i市和第j市之间修建公路,两个城市的建筑公司需要相互合作。但是,在修路的过程中,两家施工公司可能会因为沟通不畅而发生冲突,会造成建筑材料的浪费。从形式上讲,在第i个城市和第j个城市之间修建公路将浪费ged(ai, aj)建筑材料。你能帮助猫国国王选择建造n - 1条连接所有城市的道路,并最大限度地减少建筑材料的浪费吗?为了减少输入大小,猫国的国王给你一个随机整数生成器和3个参数L, R,种子。下面的C语言代码展示了如何生成n个整数a1, a2,…, an, a[i]存储第i个城市建筑公司的经验值。您可以在提交的文件中直接使用代码。
题解:
这道题本身并不是一道难题,
本身就一个最小生成树求出最小距离即可
但是边数n^2,正常求边肯定会t
关键是能否想到n > 某一个之后,答案只会是n - 1
正常来想的话是很难想到这一点的,由于我本身也不太明白,所以无法证明这一点
但是我么可以通过打表发现,当n > 5后,答案就都是n - 1了
(打表是一种很重要的思想,并且这题只用输入四个数即可,是和容易打表的,遇到一些难以解决的问题时,打表不失为一种好的选择)
此外通过他给我们的函数发现

如果R = L那么所有a[i]均为L那么答案就是(n-1)*L
#include<iostream> #include<algorithm> #include<string> #include<cstring> #include<vector> #include<map> #include<queue> using namespace std; #define int long long const int N = 4e6 + 10; typedef pair<int, int> PII; unsigned long long seed; int R,L; unsigned long long xorshift64() {unsigned long long x=seed;x^=x<<13;x^=x>>7;x^=x<<17;return seed=x; } int f[N]; int gen(){return xorshift64()%(R-L+1)+L; } int n; int a[N]; struct node {int l,r,x;friend operator <(const node &a,const node &b){return a.x < b.x;} }p[N]; int find(int x) {if(f[x] == x)return x;return f[x] = find(f[x]); } void solve() {cin >> n >> L >> R >> seed;for(int i = 1;i <= n;i++)a[i] = gen();if( L == R){cout <<(n - 1)*L;return ;}if(n > 5){cout << n - 1<<"\n";return ;}int cnt = 0;for(int i = 1;i <= n;i++){for(int j = i + 1;j <= n;j++){p[++cnt].l = i;p[cnt].r = j;p[cnt].x = __gcd(a[i],a[j]);}}for(int i = 1;i <= n;i++){f[i] = i;}sort(p+1,p+1+cnt);int ans = 0;int w = 0;for(int i = 1;i <= cnt;i++){int x = find(p[i].l);int y = find(p[i].r);if(x != y){f[y] = x;ans += p[i].x;w ++;}if(w == n-1)break;}cout << ans; }signed main() { // ios::sync_with_stdio(0); // cin.tie(0);cout.tie(0);int t = 1; // cin >> t; //scanf("%lld",&t);while (t--) {solve();} } //3 F //5 B //6 F //9 F //10 B //12 F //15 FB //18 FB
相关文章:

B - Build Roads (最小生成树 + 打表)
https://vjudge.net/problem/Gym-103118B/origin 在猫的国度里,有n个城市。猫国国王想要修n -1条路来连接所有的城市。第i市有一家ai经验价值的建筑公司。要在第i市和第j市之间修建公路,两个城市的建筑公司需要相互合作。但是,在修路的过程中…...

k8s管理工具
k8s管理工具 文章目录k8s管理工具Kuboard(💕17.3k)KubeOperator(💕4.6k)Rainbond(💕3.8k)KubeSphere(💕12k)Kuboard(&…...

Cannot start compiler The output path is not specified for module mystatic(已解决)
1.背景:今天在idea上写了一些代码,右键run竟然跑不起来了,而且右下角的Event Log还报错。报错内容如下图:2.报错原因:项目代码和编译器的输出路径不在一块,导致idea无法找到模块的output path(输…...
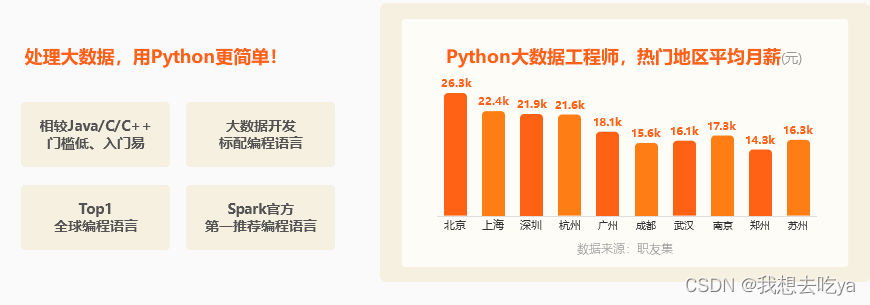
python入门应该怎么学习
国外Python的使用率非常高,但在国内Python是近几年才火起来,Python正处于高速上升期市场对于Python开发人才的需求量急剧增加,学习Python的前景比较好。 Python应用领域广泛,意味着选择Python的同学在学成之后可选择的就业领域有…...
不懂命令, 如何将代码托管到Gitee上
1.注册码云注册地址 : https://gitee.com2. 新建仓库第一步 : 创建仓库第二步 : 给仓库起名字创建好仓库后, 我们就有了一个网络上的仓库 : 3. 将网络上的仓库克隆到本地在克隆仓库之前, 我们需要先在电脑上安装以下两个工具 >>这两个软件一定要按顺序安装, 先安装第一个…...
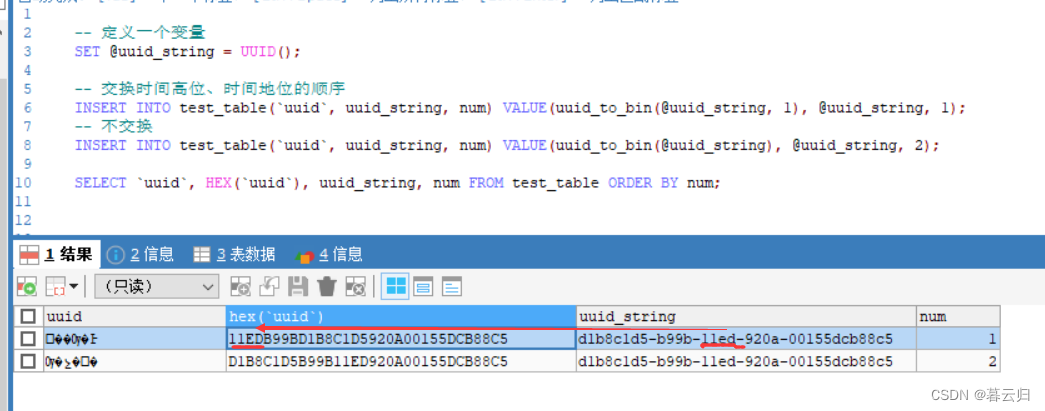
Mysql常见面试题总结
1、什么是存储引擎 存储引擎指定了表的类型,即如何存储和索引数据,是否支持事务,同时存储引擎也决定了表在计算机中的存储方式。 2、查看数据库支持哪些存储引擎使用什么命令? -- 查看数据库支持的存储引擎 show engines; 或者 …...

python第一周作业
作业1:1、PPT上五个控制台界面2、要求定义两个数,并且交换它们的值(请使用多种方式,越多越好)作业1作业2:判断一个数,是否是2的指数2的指数0000 0010 0000 00010000 0100 0000 00110000 1000 00…...
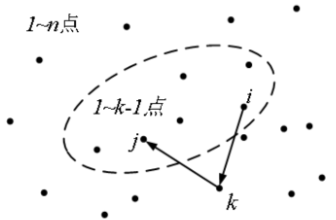
FLoyd算法的入门与应用
目录 一、前言 二、FLoyd算法 1、最短路问题 2、Floyd算法 3、Floyd的特点 4、Floyd算法思想:动态规划 三、例题 1、蓝桥公园(lanqiaoOJ题号1121) 2、路径(2021年初赛 lanqiaoOJ题号1460) 一、前言 本文主要…...

303. 区域和检索 - 数组不可变
303. 区域和检索 - 数组不可变 给定一个整数数组 nums,处理以下类型的多个查询: 计算索引 left 和 right (包含 left 和 right)之间的 nums 元素的 和 ,其中 left < right 实现 NumArray 类: NumArray(int[] num…...

Spring Cloud融合Nacos配置加载优先级 | Spring Cloud 8
一、前言 Spring Cloud Alibaba Nacos Config 目前提供了三种配置能力从 Nacos 拉取相关的配置: A:通过内部相关规则(应用名、扩展名、profiles)自动生成相关的 Data Id 配置B:通过 spring.cloud.nacos.config.extension-configs的方式支持…...
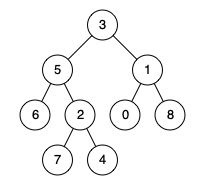
LeetCode 236.二叉树的最近公共祖先
给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。百度百科中最近公共祖先的定义为:“对于有根树 T 的两个节点 p、q,最近公共祖先表示为一个节点 x,满足 x 是 p、q 的祖先且 x 的深度尽可能大(一个节点也可以是它自己的祖…...
)
awk简单实例(持续更新中)
一 概述 awk命令是一种分析和处理文本文件的编程工具。它的功能非常强大,是Linux/Unix系统中最常用的过滤工具。 awk内建变量: NF 整个数据行(即$0)拥有的字段总数 NR 当前awk所处理的数据行的编号 $0 当前awk所处理的数据行 $1 数据行的第1个字段 $2 数…...
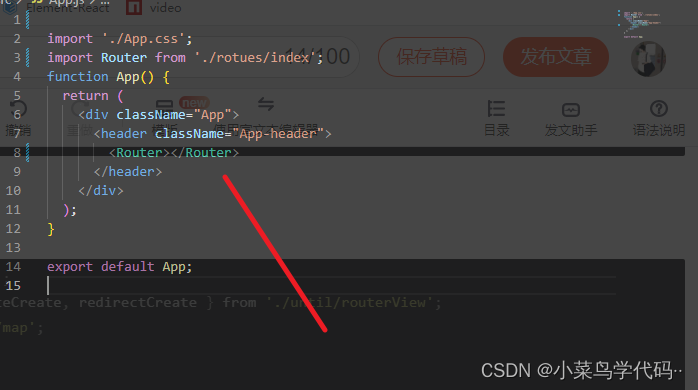
react动态路由组件的封装
react动态路由组件的封装 我这篇比较全面 首先下载包 npm i react-router-dom5 这里为什么要用5的版本为啥不用最新的,原因在于老版本跟新版本写法不一样 老版本 import { HashRouter, Route, Switch, Redirect } from react-router-dom;render() {return (<Ha…...
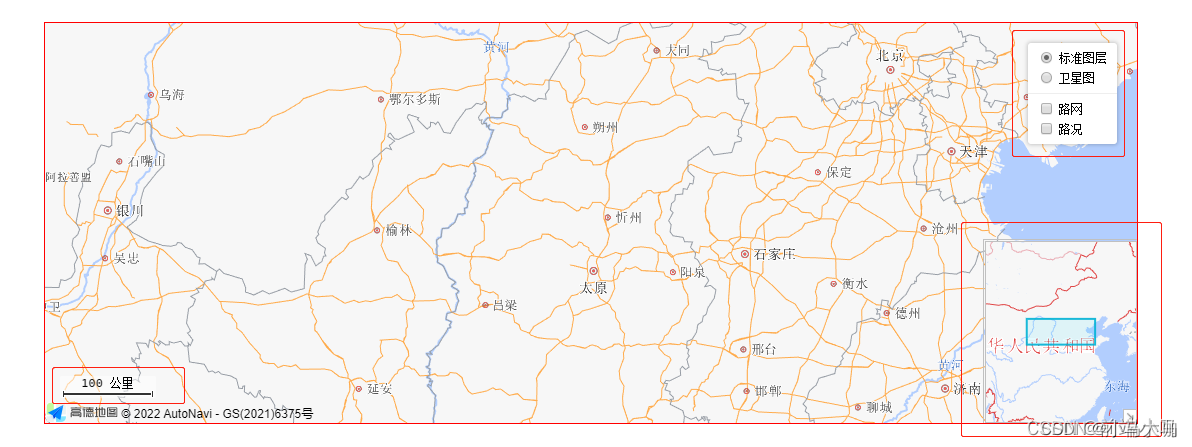
Vue项目中引入高德地图步骤详解
高德地图API官网:高德开放平台 | 高德地图API。 目录 一、案例效果 二、开发准备 1. 注册高德开放平台账号 2. 创建应用添加 key 值 三、项目中使用地图组件 1. npm 获取高德地图 API 2.在项目中新建 MapContainer.vue 文件,用作地图组件。 3.在…...

软件测试用例篇(2)
功能测试界面测试兼容性测试安全测试易用性测试性能测试 针对有需求的案例来设计测试用例:邮箱注册,部分测试用例 https://zay1xofb7z6.feishu.cn/mindnotes/bmncnKD5Ak6GSZl3PRlWDgF9z3g#mindmap 一)等价类: 场景需求:姓名长度是6-200位,那么如何进行设…...

leetcode题解-27. Remove Element
给你一个数组 nums 和一个值 val,你需要 原地 移除所有数值等于 val 的元素,并返回移除后数组的新长度。 不要使用额外的数组空间,你必须仅使用 O(1) 额外空间并 原地 修改输入数组。 元素的顺序可以改变。你不需要考虑数组中超出新长度后面…...
【fly-iot飞凡物联】(4):在linux系统上搭建arduino环境,可以使用离线包,导入到arduino上即可。
目录前言1,关于2,然后就可以找到ESP32,ESP8266的主版3,方法2,github下载,然后手动添加到ide中吧4,总结前言 本文的原文连接是: https://blog.csdn.net/freewebsys/article/details/108971807 未…...

java实例解析类图中【关联、组合和聚合】的区别
总目录链接==>> AutoSAR入门和实战系列总目录 文章目录 聚合Composition聚合与组合的区别关联是两个独立类之间的关系,它通过它们的对象建立关联。关联可以是一对一、一对多、多对一、多对多。在面向对象的编程中,一个对象与另一个对象通信以使用该对象提供的功能和服…...

基于m-p条件查询代码生成
目录 起因 演示 使用 0.自定义注解 1.定义一个dto的条件查询类 2.调用主程序 效果图 小结 代码 注解 Dto类 完整代码 起因 最近两天一直写后台管理统计的增删改查(很少写增删改查,所以不是很熟练),几乎每个表都要涉及到条件查询的业务…...
【LeetCode】带环链表两道题
第一题:环形链表 问题介绍 给你一个链表的头节点head ,判断链表中是否有环。 如果链表中有某个节点,可以通过连续跟踪next指针再次到达,则链表中存在环。为了表示给定链表中的环,评测系统内部使用整数pos 来表示链表…...

深度学习在微纳光子学中的应用
深度学习在微纳光子学中的主要应用方向 深度学习与微纳光子学的结合主要集中在以下几个方向: 逆向设计 通过神经网络快速预测微纳结构的光学响应,替代传统耗时的数值模拟方法。例如设计超表面、光子晶体等结构。 特征提取与优化 从复杂的光学数据中自…...

AI-调查研究-01-正念冥想有用吗?对健康的影响及科学指南
点一下关注吧!!!非常感谢!!持续更新!!! 🚀 AI篇持续更新中!(长期更新) 目前2025年06月05日更新到: AI炼丹日志-28 - Aud…...

零门槛NAS搭建:WinNAS如何让普通电脑秒变私有云?
一、核心优势:专为Windows用户设计的极简NAS WinNAS由深圳耘想存储科技开发,是一款收费低廉但功能全面的Windows NAS工具,主打“无学习成本部署” 。与其他NAS软件相比,其优势在于: 无需硬件改造:将任意W…...

服务器硬防的应用场景都有哪些?
服务器硬防是指一种通过硬件设备层面的安全措施来防御服务器系统受到网络攻击的方式,避免服务器受到各种恶意攻击和网络威胁,那么,服务器硬防通常都会应用在哪些场景当中呢? 硬防服务器中一般会配备入侵检测系统和预防系统&#x…...

Vue2 第一节_Vue2上手_插值表达式{{}}_访问数据和修改数据_Vue开发者工具
文章目录 1.Vue2上手-如何创建一个Vue实例,进行初始化渲染2. 插值表达式{{}}3. 访问数据和修改数据4. vue响应式5. Vue开发者工具--方便调试 1.Vue2上手-如何创建一个Vue实例,进行初始化渲染 准备容器引包创建Vue实例 new Vue()指定配置项 ->渲染数据 准备一个容器,例如: …...

Java多线程实现之Thread类深度解析
Java多线程实现之Thread类深度解析 一、多线程基础概念1.1 什么是线程1.2 多线程的优势1.3 Java多线程模型 二、Thread类的基本结构与构造函数2.1 Thread类的继承关系2.2 构造函数 三、创建和启动线程3.1 继承Thread类创建线程3.2 实现Runnable接口创建线程 四、Thread类的核心…...

SiFli 52把Imagie图片,Font字体资源放在指定位置,编译成指定img.bin和font.bin的问题
分区配置 (ptab.json) img 属性介绍: img 属性指定分区存放的 image 名称,指定的 image 名称必须是当前工程生成的 binary 。 如果 binary 有多个文件,则以 proj_name:binary_name 格式指定文件名, proj_name 为工程 名&…...

基于TurtleBot3在Gazebo地图实现机器人远程控制
1. TurtleBot3环境配置 # 下载TurtleBot3核心包 mkdir -p ~/catkin_ws/src cd ~/catkin_ws/src git clone -b noetic-devel https://github.com/ROBOTIS-GIT/turtlebot3.git git clone -b noetic https://github.com/ROBOTIS-GIT/turtlebot3_msgs.git git clone -b noetic-dev…...

PAN/FPN
import torch import torch.nn as nn import torch.nn.functional as F import mathclass LowResQueryHighResKVAttention(nn.Module):"""方案 1: 低分辨率特征 (Query) 查询高分辨率特征 (Key, Value).输出分辨率与低分辨率输入相同。"""def __…...

Java编程之桥接模式
定义 桥接模式(Bridge Pattern)属于结构型设计模式,它的核心意图是将抽象部分与实现部分分离,使它们可以独立地变化。这种模式通过组合关系来替代继承关系,从而降低了抽象和实现这两个可变维度之间的耦合度。 用例子…...
