第十四届蓝桥杯模拟赛(第三期)试题与题解 C++
目录
一、填空题
(一)最小的十六进制(答案:2730)
(二)Excel的列(答案:BYT)
(三)相等日期(答案:70910)
(四)多少种取法(答案:189)
(五)最大连通分块(答案:148)
二、编程题
(一)哪一天
(二)信号覆盖
(三)清理水草
(四)最长滑行
(五)区间最小值
一、填空题
(一)最小的十六进制(答案:2730)
问题描述
请找到一个大于 2022 的最小数,这个数转换成十六进制之后,所有的数位(不含前导 0)都为字母(A 到 F)。
请将这个数的十进制形式作为答案提交。
答案提交
这是一道结果填空的题,你只需要算出结果后提交即可。本题的结果为一个整数,在提交答案时只填写这个整数,填写多余的内容将无法得分。
可以不使用变成,直接使用计算机即可.
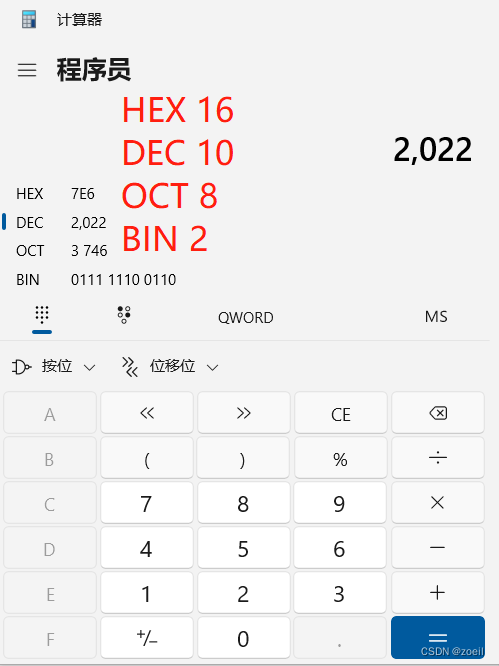
可以看到202216进制为7E6,那么要所有位数都为字母且最小,则为 AAA
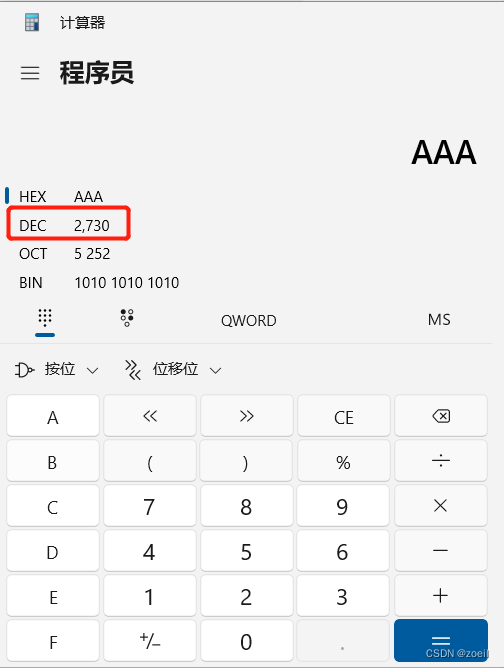
代码:
#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <vector>
#include <stack>
#include <queue>
using namespace std;
#define fi first
#define se second
typedef long long LL;
typedef pair<int, int> PII;
string get(int x) {string s = "";while(x) {int t = x % 16;x /= 16;if(t > 9) s += (t + 'A' - 10);else s += (t + '0');}reverse(s.begin(), s.end());return s;
}
bool check(string s) {for(int i = 0; i < s.size(); i ++)if(s[i] < 'A') return false;return true;
}
int main() {for(int i = 2022; i ; i ++) {string hex = get(i);if(check(hex)) {cout << i << endl;break;}}return 0;
}(二)Excel的列(答案:BYT)
问题描述
在 Excel 中,列的名称使用英文字母的组合。前 26 列用一个字母,依次为 A 到 Z,接下来 26*26 列使用两个字母的组合,依次为 AA 到 ZZ。
请问第 2022 列的名称是什么?
答案提交
这是一道结果填空的题,你只需要算出结果后提交即可。本题的结果为一个由大写字母组成的字符串,在提交答案时只填写这个字符串,填写多余的内容将无法得分。
可以直接口算,因为26*26=676,26*26*26=17576,所以2022需要三位数表示,口算过程:
2022 % 26 = 20 == T
2022 /= 26 == 77
77 % 26 == 25 == Y
77 /= 26 == 2
2 == B答案:BYT代码差不多的思路,这里就不写了
(三)相等日期(答案:70910)
问题描述
对于一个日期,我们可以计算出年份的各个数位上的数字之和,也可以分别计算月和日的各位数字之和。请问从 1900 年 1 月 1 日至 9999 年 12 月 31 日,总共有多少天,年份的数位数字之和等于月的数位数字之和加日的数位数字之和。
例如,2022年11月13日满足要求,因为 2+0+2+2=(1+1)+(1+3) 。
请提交满足条件的日期的总数量。这是一道结果填空的题,你只需要算出结果后提交即可。本题的结果为一个整数,在提交答案时只填写这个整数,填写多余的内容将无法得分。
#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <vector>
#include <stack>
#include <queue>
using namespace std;
#define fi first
#define se second
typedef long long LL;
typedef pair<int, int> PII;int month[] = {0, 31, 28, 31, 30, 31, 30, 31, 31, 30, 31, 30, 31};
int get(int x) {int res = 0;while(x) {res += x % 10;x /= 10;}return res;
}
int main() {int ans = 0;for(int i = 1900; i <= 9999; i ++) {int syear = get(i);bool is_leap = !(i % 400) || (i % 100 && !(i % 4));for(int j = 1; j <= 12; j ++) {if(j == 2 && is_leap) month[2] = 29;else month[2] = 28;for(int k = 1; k <= month[j]; k ++){int smd = get(j) + get(k);if(smd == syear) {ans ++;}}}}cout << ans << endl;return 0;
}(四)多少种取法(答案:189)
问题描述
小蓝有 30 个数,分别为:99, 22, 51, 63, 72, 61, 20, 88, 40, 21, 63, 30, 11, 18, 99, 12, 93, 16, 7, 53, 64, 9, 28, 84, 34, 96, 52, 82, 51, 77 。
小蓝可以在这些数中取出两个序号不同的数,共有 30*29/2=435 种取法。
请问这 435 种取法中,有多少种取法取出的两个数的乘积大于等于 2022 。
答案提交
这是一道结果填空的题,你只需要算出结果后提交即可。本题的结果为一个整数,在提交答案时只填写这个整数,填写多余的内容将无法得分。
#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <vector>
#include <stack>
#include <queue>
using namespace std;
#define fi first
#define se second
typedef long long LL;
typedef pair<int, int> PII;
int a[] = {99, 22, 51, 63, 72, 61, 20, 88, 40, 21, 63, 30, 11, 18, 99, 12, 93, 16, 7, 53, 64, 9, 28, 84, 34, 96, 52, 82, 51, 77};
int main() {int res = 0;for(int i = 0; i < 30; i ++)for(int j = i + 1; j < 30; j ++)if(i != j && a[i] * a[j] >= 2022)res ++;cout << res << endl;return 0;
}(五)最大连通分块(答案:148)
问题描述
小蓝有一个 30 行 60 列的数字矩阵,矩阵中的每个数都是 0 或 1 。
110010000011111110101001001001101010111011011011101001111110
010000000001010001101100000010010110001111100010101100011110
001011101000100011111111111010000010010101010111001000010100
101100001101011101101011011001000110111111010000000110110000
010101100100010000111000100111100110001110111101010011001011
010011011010011110111101111001001001010111110001101000100011
101001011000110100001101011000000110110110100100110111101011
101111000000101000111001100010110000100110001001000101011001
001110111010001011110000001111100001010101001110011010101110
001010101000110001011111001010111111100110000011011111101010
011111100011001110100101001011110011000101011000100111001011
011010001101011110011011111010111110010100101000110111010110
001110000111100100101110001011101010001100010111110111011011
111100001000001100010110101100111001001111100100110000001101
001110010000000111011110000011000010101000111000000110101101
100100011101011111001101001010011111110010111101000010000111
110010100110101100001101111101010011000110101100000110001010
110101101100001110000100010001001010100010110100100001000011
100100000100001101010101001101000101101000000101111110001010
101101011010101000111110110000110100000010011111111100110010
101111000100000100011000010001011111001010010001010110001010
001010001110101010000100010011101001010101101101010111100101
001111110000101100010111111100000100101010000001011101100001
101011110010000010010110000100001010011111100011011000110010
011110010100011101100101111101000001011100001011010001110011
000101000101000010010010110111000010101111001101100110011100
100011100110011111000110011001111100001110110111001001000111
111011000110001000110111011001011110010010010110101000011111
011110011110110110011011001011010000100100101010110000010011
010011110011100101010101111010001001001111101111101110011101
如果从一个标为 1 的位置可以通过上下左右走到另一个标为 1 的位置,则称两个位置连通。与某一个标为 1 的位置连通的所有位置(包括自己)组成一个连通分块。
请问矩阵中最大的连通分块有多大?
答案提交
这是一道结果填空的题,你只需要算出结果后提交即可。本题的结果为一个整数,在提交答案时只填写这个整数,填写多余的内容将无法得分。
宽搜即可
#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <vector>
#include <stack>
#include <queue>
using namespace std;
#define fi first
#define se second
typedef long long LL;
typedef pair<int, int> PII;
char g[35][65];
bool st[35][65];
int n = 30, m = 60;
int dx[] = {1, 0, -1, 0}, dy[] = {0, 1, 0, -1};
int bfs(int u, int v) {int ans = 1;st[u][v] = true;queue<PII> q;q.push({u, v});while(q.size()) {auto t = q.front();q.pop();for(int i = 0; i < 4; i ++) {int x = dx[i] + t.fi, y = dy[i] + t.se;if(x < 1 || x > n || y < 1 || y > m) continue;if(st[x][y]) continue;if(g[x][y] == '1') {st[x][y] = true;q.push({x, y});ans ++;}}}return ans;
}
int main() {memset(st, 0, sizeof st);for(int i = 1; i <= 30; i ++)for(int j = 1; j <= 60; j ++)cin >> g[i][j];int res = 0;for(int i = 1; i <= 30; i ++)for(int j = 1; j <= 60; j ++)if(!st[i][j] && g[i][j] == '1'){res = max(res, bfs(i, j));}cout << res << endl;return 0;}二、编程题
(一)哪一天
问题描述
给定一天是一周中的哪天,请问 n 天后是一周中的哪天?
输入格式
输入第一行包含一个整数 w,表示给定的天是一周中的哪天,w 为 1 到 6 分别表示周一到周六,w 为 7 表示周日。
第二行包含一个整数 n。
输出格式
输出一行包含一个整数,表示 n 天后是一周中的哪天,1 到 6 分别表示周一到周六,7 表示周日。
样例输入
6
10
样例输出
2
评测用例规模与约定
对于所有评测用例,1 <= n <= 1000000。
day等于7得时需要特判一下输出7
#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <vector>
#include <stack>
#include <queue>
using namespace std;
#define fi first
#define se second
typedef long long LL;
typedef pair<int, int> PII;
int main() {int day, w;cin >> day >> w;w %= 7;day += w;day %= 7;cout << (day == 0 ? 7 : day) << endl;return 0;
} (二)信号覆盖
问题描述
小蓝负责一块区域的信号塔安装,整块区域是一个长方形区域,建立坐标轴后,西南角坐标为 (0, 0), 东南角坐标为 (W, 0), 西北角坐标为 (0, H), 东北角坐标为 (W, H)。其中 W, H 都是整数。
他在 n 个位置设置了信号塔,每个信号塔可以覆盖以自己为圆心,半径为 R 的圆形(包括边缘)。
为了对信号覆盖的情况进行检查,小蓝打算在区域内的所有横纵坐标为整数的点进行测试,检查信号状态。其中横坐标范围为 0 到 W,纵坐标范围为 0 到 H,总共测试 (W+1) * (H+1) 个点。
给定信号塔的位置,请问这 (W+1)*(H+1) 个点中有多少个点被信号覆盖。输入第一行包含四个整数 W, H, n, R,相邻整数之间使用一个空格分隔。
接下来 n 行,每行包含两个整数 x, y,表示一个信号塔的坐标。信号塔可能重合,表示两个信号发射器装在了同一个位置。输出一行包含一个整数,表示答案。
样例输入
10 10 2 5
0 0
7 057
对于所有评测用例,1 <= W, H <= 100,1 <= n <= 100, 1 <= R <= 100, 0 <= x <= W, 0 <= y <= H。
编程题 2 枚举每个点到每个哨站的距离 10000*100 = 1e6 不会爆
#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <vector>
#include <stack>
#include <queue>
using namespace std;
#define fi first
#define se second
typedef long long LL;
typedef pair<int, int> PII;
int w, h, n, r;
PII p[105];
bool st[105][105];
int main() {cin >> w >> h >> n >> r;for(int i = 0; i < n; i ++){int x, y;scanf("%d%d", &x, &y);p[i] = {x, y};st[x][y] = true;}for(int i = 0; i <= w; i ++)for(int j = 0; j <= h; j ++){for(int k = 0; k < n; k ++) {if(st[i][j]) break;double dist = sqrt(abs(p[k].fi - i) * abs(p[k].fi - i) + abs(p[k].se - j) * abs(p[k].se - j) );if(dist <= r) {st[i][j] = true;break;}}}int res = 0;for(int i = 0; i <= w; i ++)for(int j = 0; j <= h; j ++){if(st[i][j]) res ++;}cout << res << endl;return 0;
}(三)清理水草
问题描述
小蓝有一个 n * m 大小的矩形水域,小蓝将这个水域划分为 n 行 m 列,行数从 1 到 n 标号,列数从 1 到 m 标号。每行和每列的宽度都是单位 1 。
现在,这个水域长满了水草,小蓝要清理水草。
每次,小蓝可以清理一块矩形的区域,从第 r1 行(含)到第 r2 行(含)的第 c1 列(含)到 c2 列(含)。
经过一段时间清理后,请问还有多少地方没有被清理过。输入第一行包含两个整数 n, m,用一个空格分隔。
第二行包含一个整数 t ,表示清理的次数。
接下来 t 行,每行四个整数 r1, c1, r2, c2,相邻整数之间用一个空格分隔,表示一次清理。请注意输入的顺序。输出一行包含一个整数,表示没有被清理过的面积。
样例输入1
2 3
2
1 1 1 3
1 2 2 22
30 20
2
5 5 10 15
6 7 15 9519
对于所有评测用例,1 <= r1 <= r2 <= n <= 100, 1 <= c1 <= c2 <= m <= 100, 0 <= t <= 100。
编程题 3 二维前缀和
#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <vector>
#include <stack>
#include <queue>
using namespace std;
#define fi first
#define se second
typedef long long LL;
typedef pair<int, int> PII;
int n, m;
int g[105][105];
void insert(int x1, int y1, int x2, int y2) {g[x1][y1] += 1;g[x2 + 1][y1] -= 1;g[x1][y2 + 1] -= 1;g[x2 + 1][y2 + 1] += 1;
}
int main() {int t;cin >> n >> m >> t;int x1, x2, y1, y2;for(int i = 0; i < t; i ++) {scanf("%d%d%d%d", &x1, &y1, &x2, &y2);insert(x1, y1, x2, y2);}for(int i = 1; i <= n; i ++)for(int j = 1; j <= m; j ++)g[i][j] += g[i - 1][j] + g[i][j - 1] - g[i - 1][j - 1];int res = 0;for(int i = 1; i <= n; i ++)for(int j = 1; j <= m; j ++)if(!g[i][j]) res ++;cout << res << endl;return 0;
}(四)最长滑行
问题描述
小蓝准备在一个空旷的场地里面滑行,这个场地的高度不一,小蓝用一个 n 行 m 列的矩阵来表示场地,矩阵中的数值表示场地的高度。
如果小蓝在某个位置,而他上、下、左、右中有一个位置的高度(严格)低于当前的高度,小蓝就可以滑过去,滑动距离为 1 。
如果小蓝在某个位置,而他上、下、左、右中所有位置的高度都大于等于当前的高度,小蓝的滑行就结束了。
小蓝不能滑出矩阵所表示的场地。
小蓝可以任意选择一个位置开始滑行,请问小蓝最多能滑行多远距离。
输入格式
输入第一行包含两个整数 n, m,用一个空格分隔。
接下来 n 行,每行包含 m 个整数,相邻整数之间用一个空格分隔,依次表示每个位置的高度。
输出格式
输出一行包含一个整数,表示答案。
样例输入
4 5
1 4 6 3 1
11 8 7 3 1
9 4 5 2 1
1 3 2 2 1
样例输出
7
样例说明
滑行的位置一次为 (2, 1), (2, 2), (2, 3), (3, 3), (3, 2), (4, 2), (4, 3)。
评测用例规模与约定
对于 30% 评测用例,1 <= n <= 20,1 <= m <= 20,0 <= 高度 <= 100。
对于所有评测用例,1 <= n <= 100,1 <= m <= 100,0
自己写的时候没想到记忆化搜索,对于这块知识点了解的也比较少,直接使用dfs暴力了
// 编程题 4 暴力递归
#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <vector>
#include <stack>
#include <queue>
using namespace std;
#define fi first
#define se second
typedef long long LL;
typedef pair<int, int> PII;
int n, m;
int g[105][105];
bool st[105][105];
int res = 0;
int dx[] = {0, 1, 0, -1}, dy[] = {1, 0, -1, 0};
void dfs(int u, int v, int cnt) {res = max(res, cnt);for(int i = 0; i < 4; i ++) {int x = dx[i] + u, y = dy[i] + v;if(x < 1 || x > n || y < 1 || y > n) continue;if(g[x][y] <= g[u][v]) continue;if(st[x][y]) continue;st[x][y] = true;dfs(x, y, cnt + 1);st[x][y] = false;}
}
int main() {cin >> n >> m;for(int i = 1; i <= n; i ++)for(int j = 1; j <= m; j ++){scanf("%d", &g[i][j]); }for(int i = 1; i <= n; i ++)for(int j = 1; j <= m; j ++){st[i][j] = true;dfs(i, j, 1);st[i][j] = false;}cout << res << endl; return 0;
}网上了解到的记忆化搜索
#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <vector>
#include <stack>
#include <queue>
using namespace std;
#define fi first
#define se second
typedef long long LL;
typedef pair<int, int> PII;
int n, m, res;
int g[105][105];
int dist[105][105];
int dx[] = {0, 1, 0, -1}, dy[] = {1, 0, -1, 0};
int dfs(int u, int v) {if(dist[u][v] != -1) return dist[u][v];dist[u][v] = 1;for(int i = 0; i < 4; i ++) {int x = dx[i] + u, y = dy[i] + v;if(x < 1 || x > n || y < 1 || y > n) continue;if(g[x][y] <= g[u][v]) continue;dist[u][v] = max(dist[u][v], dfs(x, y) + 1);}return dist[u][v];
}
int main() {cin >> n >> m;for(int i = 1; i <= n; i ++)for(int j = 1; j <= m; j ++){scanf("%d", &g[i][j]); }memset(dist, -1, sizeof dist);for(int i = 1; i <= n; i ++)for(int j = 1; j <= m; j ++){res = max(res, dfs(i, j));}cout << res << endl; return 0;
}(五)区间最小值
小蓝有一个序列a[1], a[2]. .... a[n].
给定一个正整数k,请问对于每一个1到n之间的序号i,a[i-k], a[i-k+1].... a[i+k]这2k+1个数中的最小值是多少?当某个下标超过1到n的范围时,数不存在,求最小值时只取存在的那些值。
输入格式
输入的第一行包含一整数n。
第二行包含n个整数,分别表示a[1], a[2]. ... a[n]。第三行包含一个整数k。
输出格式
输出一行,包含n个整数,分别表示对于每个序号求得的最小值。
样例输入
5
5 2 7 4 3
1
样例输出
2 2 2 3 3
评测用例规模与约定
对于30%的评测用例,1<= n<= 1000,1 <= a[i]<=1000。
对于50%的评测用例,1<= n<= 10000,1 <= a[]<=10000。
对于所有评测用例,1<= n<= 1000000,1 <= a[i]<=100000。
可转化为求每个数左边2k范围内最小的数字,使用单调队列即可
#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <vector>
#include <stack>
#include <queue>
using namespace std;
#define fi first
#define se second
typedef long long LL;
typedef pair<int, int> PII;
const int N = 1000005;
int a[N];
int q[N], tt = -1, hh = 0;
int main() {int n, k;cin >> n;for(int i = 0; i < n; i ++) {scanf("%d", &a[i]);}cin >> k;for(int i = 0; i < n; i ++) {while(tt >= hh && a[q[tt]] >= a[i]) tt --;while(tt >= hh && i - q[hh] + 1 > 2 * k + 1) hh ++;q[++ tt] = i;if(i >= k)printf("%d ", a[q[hh]]);}for(int i = 0; i < k; i ++)printf("%d ", a[q[hh]]);return 0;
} 赛后看到网上有使用ST表的,蒟蒻完全没学过
总结:
萌新一个,有错误或者有更好的做法请各位大佬评论区提出和讨论
相关文章:

第十四届蓝桥杯模拟赛(第三期)试题与题解 C++
目录 一、填空题 (一)最小的十六进制(答案:2730) (二)Excel的列(答案:BYT) (三)相等日期(答案:70910) (四)多少种取法(答案:189)…...

关于 “宏“
起源 宏 Macro"这个词源于希腊语 “makros”,意为“大的,长的” 延伸使用 随后用于计算机领域是,在汇编语言时用于描述一大堆的汇编指令。 只要用宏指令,就是直接用的一大堆的汇编指令(有点函数的味道…...

1.2 CSS标签选择器,类选择器
CSS选择器: 根据不同的需求选出不同的标签,进行美化装饰 1. 标签选择器 标签选择器(元素选择器):用 HTML标签名作为选择器,按标签名称进行分类,为页面某一类标签指定统一的CSS样式 作用: 可以把某一类标签全部选中&…...

【Linux】进程等待 | 详解 wait/waitpid 的 status 参数
🤣 爆笑教程 👉 《看表情包学Linux》👈 猛戳订阅 🔥 💭 写在前面:在上一章中我们讲解了进程创建与进程终止,本章我们开始讲解进程等待。进程等待这部分知识相较于前面还是较为复杂的࿰…...

OpenAI眼中的无线调优策略
问:无线调优策略该怎么优化无线调优是指对无线网络的各种参数进行优化,以提高网络性能和用户体验。以下是几个无线调优策略:频谱分配:通过优化频谱的分配,可以提高网络的容量和覆盖范围。在频谱分配时,需要…...
DataX入门
目录 1. DataX介绍 2. DataX支持的常用数据源类型 3. 设计理念 4. DataX框架设计 4.1. Reader 4.2. Writer 4.3. Framework 5. DataX的运行流程 6. DataX与Sqoop对比 7. 部署 8. 配置详解 9. 案例 同步MySql到HDFS 9.1. 整体结构 9.2. mySqlReader 9.2.1. …...

第二章SpringBoot基础学习
文章目录SpringBoot依赖管理特性依赖管理开发导入starter场景启动器SpringBoot自动配置特性自动配好Tomcat自动配好SpringMVC默认的包结构各种配置拥有默认值按需加载所有自动配置项SpringBoot注解底层注解ConfigurationImport导入组件Conditional条件装配ImportResource导入Sp…...

B - Build Roads (最小生成树 + 打表)
https://vjudge.net/problem/Gym-103118B/origin 在猫的国度里,有n个城市。猫国国王想要修n -1条路来连接所有的城市。第i市有一家ai经验价值的建筑公司。要在第i市和第j市之间修建公路,两个城市的建筑公司需要相互合作。但是,在修路的过程中…...

k8s管理工具
k8s管理工具 文章目录k8s管理工具Kuboard(💕17.3k)KubeOperator(💕4.6k)Rainbond(💕3.8k)KubeSphere(💕12k)Kuboard(&…...

Cannot start compiler The output path is not specified for module mystatic(已解决)
1.背景:今天在idea上写了一些代码,右键run竟然跑不起来了,而且右下角的Event Log还报错。报错内容如下图:2.报错原因:项目代码和编译器的输出路径不在一块,导致idea无法找到模块的output path(输…...
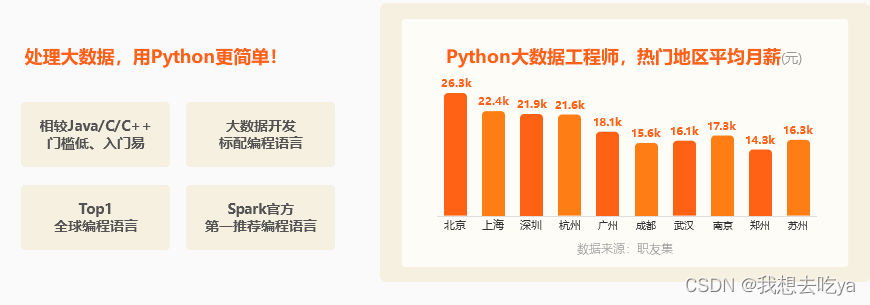
python入门应该怎么学习
国外Python的使用率非常高,但在国内Python是近几年才火起来,Python正处于高速上升期市场对于Python开发人才的需求量急剧增加,学习Python的前景比较好。 Python应用领域广泛,意味着选择Python的同学在学成之后可选择的就业领域有…...
不懂命令, 如何将代码托管到Gitee上
1.注册码云注册地址 : https://gitee.com2. 新建仓库第一步 : 创建仓库第二步 : 给仓库起名字创建好仓库后, 我们就有了一个网络上的仓库 : 3. 将网络上的仓库克隆到本地在克隆仓库之前, 我们需要先在电脑上安装以下两个工具 >>这两个软件一定要按顺序安装, 先安装第一个…...
Mysql常见面试题总结
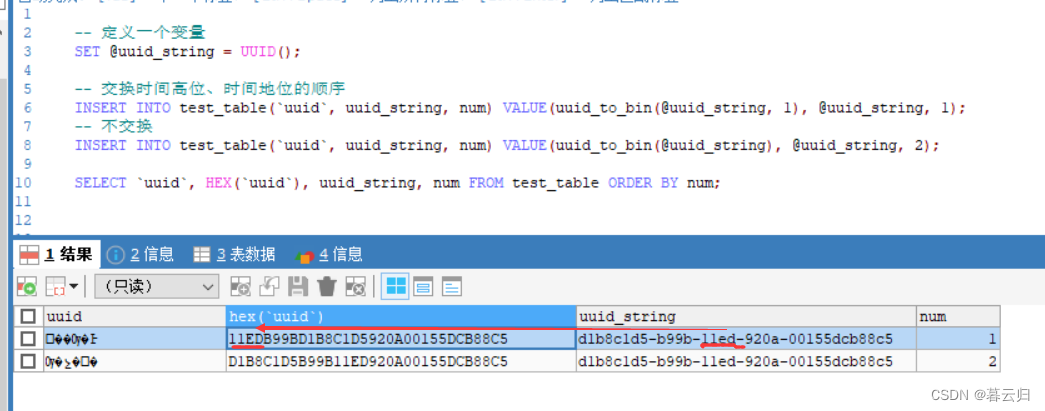
1、什么是存储引擎 存储引擎指定了表的类型,即如何存储和索引数据,是否支持事务,同时存储引擎也决定了表在计算机中的存储方式。 2、查看数据库支持哪些存储引擎使用什么命令? -- 查看数据库支持的存储引擎 show engines; 或者 …...

python第一周作业
作业1:1、PPT上五个控制台界面2、要求定义两个数,并且交换它们的值(请使用多种方式,越多越好)作业1作业2:判断一个数,是否是2的指数2的指数0000 0010 0000 00010000 0100 0000 00110000 1000 00…...
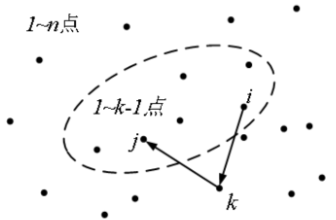
FLoyd算法的入门与应用
目录 一、前言 二、FLoyd算法 1、最短路问题 2、Floyd算法 3、Floyd的特点 4、Floyd算法思想:动态规划 三、例题 1、蓝桥公园(lanqiaoOJ题号1121) 2、路径(2021年初赛 lanqiaoOJ题号1460) 一、前言 本文主要…...

303. 区域和检索 - 数组不可变
303. 区域和检索 - 数组不可变 给定一个整数数组 nums,处理以下类型的多个查询: 计算索引 left 和 right (包含 left 和 right)之间的 nums 元素的 和 ,其中 left < right 实现 NumArray 类: NumArray(int[] num…...

Spring Cloud融合Nacos配置加载优先级 | Spring Cloud 8
一、前言 Spring Cloud Alibaba Nacos Config 目前提供了三种配置能力从 Nacos 拉取相关的配置: A:通过内部相关规则(应用名、扩展名、profiles)自动生成相关的 Data Id 配置B:通过 spring.cloud.nacos.config.extension-configs的方式支持…...
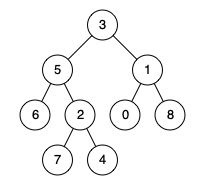
LeetCode 236.二叉树的最近公共祖先
给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。百度百科中最近公共祖先的定义为:“对于有根树 T 的两个节点 p、q,最近公共祖先表示为一个节点 x,满足 x 是 p、q 的祖先且 x 的深度尽可能大(一个节点也可以是它自己的祖…...
)
awk简单实例(持续更新中)
一 概述 awk命令是一种分析和处理文本文件的编程工具。它的功能非常强大,是Linux/Unix系统中最常用的过滤工具。 awk内建变量: NF 整个数据行(即$0)拥有的字段总数 NR 当前awk所处理的数据行的编号 $0 当前awk所处理的数据行 $1 数据行的第1个字段 $2 数…...
react动态路由组件的封装
react动态路由组件的封装 我这篇比较全面 首先下载包 npm i react-router-dom5 这里为什么要用5的版本为啥不用最新的,原因在于老版本跟新版本写法不一样 老版本 import { HashRouter, Route, Switch, Redirect } from react-router-dom;render() {return (<Ha…...

LBE-LEX系列工业语音播放器|预警播报器|喇叭蜂鸣器的上位机配置操作说明
LBE-LEX系列工业语音播放器|预警播报器|喇叭蜂鸣器专为工业环境精心打造,完美适配AGV和无人叉车。同时,集成以太网与语音合成技术,为各类高级系统(如MES、调度系统、库位管理、立库等)提供高效便捷的语音交互体验。 L…...

Flask RESTful 示例
目录 1. 环境准备2. 安装依赖3. 修改main.py4. 运行应用5. API使用示例获取所有任务获取单个任务创建新任务更新任务删除任务 中文乱码问题: 下面创建一个简单的Flask RESTful API示例。首先,我们需要创建环境,安装必要的依赖,然后…...

令牌桶 滑动窗口->限流 分布式信号量->限并发的原理 lua脚本分析介绍
文章目录 前言限流限制并发的实际理解限流令牌桶代码实现结果分析令牌桶lua的模拟实现原理总结: 滑动窗口代码实现结果分析lua脚本原理解析 限并发分布式信号量代码实现结果分析lua脚本实现原理 双注解去实现限流 并发结果分析: 实际业务去理解体会统一注…...

智能仓储的未来:自动化、AI与数据分析如何重塑物流中心
当仓库学会“思考”,物流的终极形态正在诞生 想象这样的场景: 凌晨3点,某物流中心灯火通明却空无一人。AGV机器人集群根据实时订单动态规划路径;AI视觉系统在0.1秒内扫描包裹信息;数字孪生平台正模拟次日峰值流量压力…...

什么?连接服务器也能可视化显示界面?:基于X11 Forwarding + CentOS + MobaXterm实战指南
文章目录 什么是X11?环境准备实战步骤1️⃣ 服务器端配置(CentOS)2️⃣ 客户端配置(MobaXterm)3️⃣ 验证X11 Forwarding4️⃣ 运行自定义GUI程序(Python示例)5️⃣ 成功效果
【学习笔记】深入理解Java虚拟机学习笔记——第4章 虚拟机性能监控,故障处理工具
第2章 虚拟机性能监控,故障处理工具 4.1 概述 略 4.2 基础故障处理工具 4.2.1 jps:虚拟机进程状况工具 命令:jps [options] [hostid] 功能:本地虚拟机进程显示进程ID(与ps相同),可同时显示主类&#x…...

算法岗面试经验分享-大模型篇
文章目录 A 基础语言模型A.1 TransformerA.2 Bert B 大语言模型结构B.1 GPTB.2 LLamaB.3 ChatGLMB.4 Qwen C 大语言模型微调C.1 Fine-tuningC.2 Adapter-tuningC.3 Prefix-tuningC.4 P-tuningC.5 LoRA A 基础语言模型 A.1 Transformer (1)资源 论文&a…...

如何更改默认 Crontab 编辑器 ?
在 Linux 领域中,crontab 是您可能经常遇到的一个术语。这个实用程序在类 unix 操作系统上可用,用于调度在预定义时间和间隔自动执行的任务。这对管理员和高级用户非常有益,允许他们自动执行各种系统任务。 编辑 Crontab 文件通常使用文本编…...

JavaScript 数据类型详解
JavaScript 数据类型详解 JavaScript 数据类型分为 原始类型(Primitive) 和 对象类型(Object) 两大类,共 8 种(ES11): 一、原始类型(7种) 1. undefined 定…...

FFmpeg:Windows系统小白安装及其使用
一、安装 1.访问官网 Download FFmpeg 2.点击版本目录 3.选择版本点击安装 注意这里选择的是【release buids】,注意左上角标题 例如我安装在目录 F:\FFmpeg 4.解压 5.添加环境变量 把你解压后的bin目录(即exe所在文件夹)加入系统变量…...
