概率论与数理统计————3.随机变量及其分布
一、随机变量
设E是一个随机试验,S为样本空间,样本空间的任意样本点e可以通过特定的对应法则X,使得每个样本点都有与之对应的数对应,则称X=X(e)为随机变量

二、分布函数
分布函数:设X为随机变量,x是任意实数,则事件{Xx}为随机变量X的分布函数,记为F(x)
即:F(x)=P(Xx)
(1)几何意义:

(2)某点处的概率:P(a)=P(Xa)-P(X<a)


性质:
(1)非负性:0F(x)
1
(2)规范性:F()=1;F(-
)=0
(3)单调不减函数
(4)右连续性
例:随机变量的分布函数F(x)=a+ x>0;F(x)=c x
0

 三、离散型随机变量及其分布
三、离散型随机变量及其分布
离散型随机变量 :X的取值为有限个或者无限可列个
如:X=骰子出现的点数
分布律(概率分布):

存在:P1+P2+........+Pn=1
(1)0—1分布=
,满足0—1分布

(2)二项分布
P(X=k)= 记作:X~B(n,p)
独立重复n次试验;每次试验只有两种试验结果;试验中的概率不会发生变化
(3)泊松分布
P(X=k)= 记作:X~P(
)或X~
(4)超几何分布
(5)几何分布
P(X=k)=(1-p) · P
相关文章:
概率论与数理统计————3.随机变量及其分布
一、随机变量 设E是一个随机试验,S为样本空间,样本空间的任意样本点e可以通过特定的对应法则X,使得每个样本点都有与之对应的数对应,则称XX(e)为随机变量 二、分布函数 分布函数:设X为随机变量…...

掌握单例模式的极致挑战:能否默写饿汉式代码?
目录 1.前言 2.本质 3.代码默写 1.前言 在面试中,理解和掌握单例模式是非常重要的。本文旨在帮助读者深入理解饿汉式单例模式,并通过简洁明了的解释和示例代码,使读者能够轻松掌握并默写出饿汉式单例模式的代码实现。 2.本质 饿汉式单例模…...

力扣刷MySQL-第三弹(详细讲解)
🎉欢迎您来到我的MySQL基础复习专栏 ☆* o(≧▽≦)o *☆哈喽~我是小小恶斯法克🍹 ✨博客主页:小小恶斯法克的博客 🎈该系列文章专栏:力扣刷题讲解-MySQL 🍹文章作者技术和水平很有限,如果文中出…...
PXE和kickstart无人值守安装
PXE高效批量网络装机 引言 1.系统装机的引导方式 启动 操作 系统 1.硬盘 2.光驱(u盘) 3.网络启动 pxe 重装系统? 在已有操作系统 新到货了一台服务器, 装操作系统 系统镜像 u盘 光盘 pe: 小型的 操作系统 在操…...
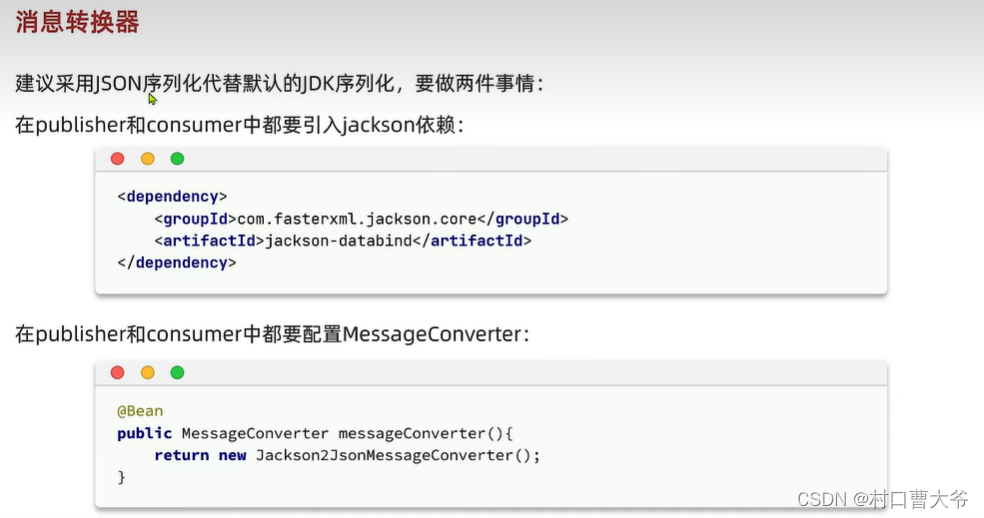
rabbitmq基础教程(ui,java,springamqp)
概述:安装看我上篇文章Docker安装rabbitmq-CSDN博客 任务一 创建一个队列 这样创建两个队列 在amq.fanout交换机里面发送数据 模拟发送数据 发送消息,发现一下信息: 所以得出理论,消息发送是先到交换机,然后由交换机…...

无重复字符的最长子串[中等]
优质博文:IT-BLOG-CN 一、题目 给定一个字符串s,请你找出其中不含有重复字符的最长子串的长度。 示例 1: 输入: s "abcabcbb" 输出: 3 解释: 因为无重复字符的最长子串是"abc",所以其长度为3。 示例 2: 输入: s &…...

考研经验总结——目录
文章目录 一、写作顺序二、个人情况说明三、读评论四、一些小牢骚五、一些注意事项(持续更新) 一、写作顺序 我将准备从三个阶段开始介绍吧 考研前考研中考研后(也就是现在我的这种情况) 考研前我会分为:数学、专业…...

Docker(一)简介和基本概念
一、简介 本章将带领你进入 Docker 的世界。 什么是 Docker? 用它会带来什么样的好处? 好吧,让我们带着问题开始这神奇之旅。 1.什么是 Docker Docker 最初是 dotCloud 公司创始人 Solomon Hykes 在法国期间发起的一个公司内部项目&…...
openssl3.2 - 官方demo学习 - test - certs
文章目录 openssl3.2 - 官方demo学习 - test - certs概述笔记.sh的执行语句打印的方法要修改的实际函数END openssl3.2 - 官方demo学习 - test - certs 概述 官方demos目录有证书操作的例子 已经做了笔记 openssl3.2 - 官方demo学习 - certs 但是这个demos/certs目录的脚本,…...
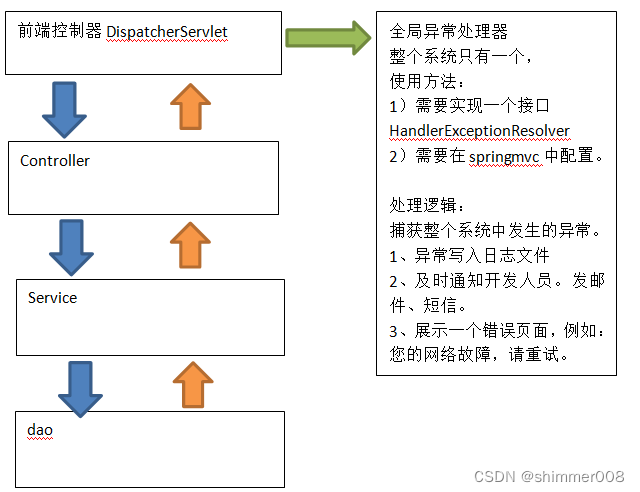
Spring MVC学习之——异常处理器
异常处理器 如果不加以异常处理,错误信息肯定会抛在浏览器页面上,这样很不友好,所以必须进行异常处理。 1.异常处理思路 系统的dao、service、controller出现都通过throws Exception向上抛出,最后由springmvc前端控制器交由异常…...
:HMAC Authentication)
HTTP API 认证技术详解(四):HMAC Authentication
目录 什么是 HMAC Authentication 认证 HMAC Authentication 原理 HMAC Authentication 认证的步骤 使用 Golang 实现 HMAC Authentication 认证 HMAC Authentication 认证的安全性 HMAC 认证的最佳实践 小结 HTTP API 认证技术主要用于验证客户端身份,并确保…...
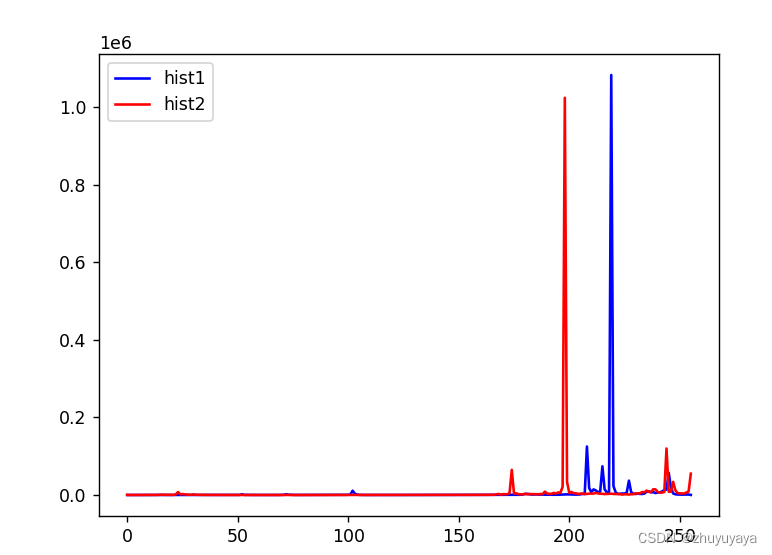
如何绘制出图像的色素分布直方图
效果 如图,可以展示出我们的图像的颜色分布直方图,表明的图像的亮和暗 实现可视化色素分布直方图方法 这里我们对我们的灰色图片和彩色图片进行了直方图显示 import cv2 import matplotlib.pyplot as plt image cv2.imread("test.jpg") # 彩色图片->…...

esp32-c-简单应用笔记
1、资料 ESP32 开发环境 Espressif-IDE: https://blog.csdn.net/chuner0425/article/details/123466848 https://blog.csdn.net/bin_zhang1/article/details/129993820?utm_mediumdistribute.pc_relevant.none-task-blog-2defaultbaidujs_baidulandingword~default-0-1299938…...

What is `XSS` does?
跨站脚本攻击(Cross-Site Scripting,XSS)是一种针对网站应用程序的安全漏洞,允许攻击者将恶意脚本注入到其他用户查看的网页中。当这些用户访问受感染的页面时,他们的浏览器会执行这些恶意脚本,导致各种安全…...
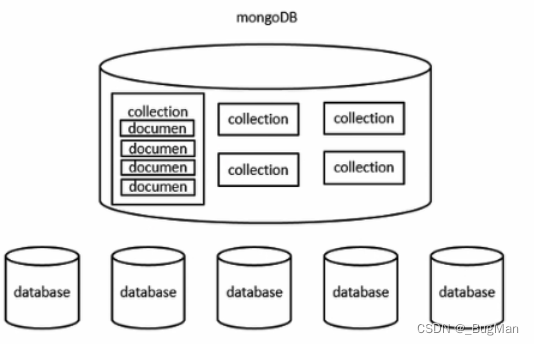
【文档数据库】ES和MongoDB的对比
目录 1.由文档存储牵出的问题 2.什么是MongoDB? 3.ES和MongoDB的对比 1.由文档存储牵出的问题 本文或者说关于mongodb的这个系列文章的源头: 前面我们聊过了分布式链路追踪系统,在基于日志实现的分布式链路追踪的方式seluthzipkin中为了…...

VUE工程化项目--vue组件化
组件化开发 & 根组件 : ① 组件化: 一个页面可以拆分成 一个个组件 ,每个组件有着自己独立的 结构、样式、行为 。 好处:便于 维护 ,利于 复用 → 提升 开发效率 。 组件分类:普通组件、根组件。 …...

iOS base64 转 data |图片Base64转NSData | UIImageView | UIImage
Api 接口返回 base64 图片字符串,需要显示在UIImageView 上。 假设 string类型的 base64ImageStr 为 api返回的 base64字符串 将base64字符串进行处理 //去除掉首尾的空白字符和换行字符NSString * img64 [img stringByTrimmingCharactersInSet:[NSCharacterSet …...

Unity面试笔记:Unity常见关键词概念
Unity面试笔记:Unity常见关键词概念 Invoke 延迟函数 和 Coroutine协程 和 Thread线程帧缓冲区(Frame buffer)颜色缓冲区(Color buffer)深度缓冲区(Depth buffer)模板缓冲区(Stencil…...

gRPC vs HTTP
性能 gRPC 消息使用 Protobuf(一种高效的二进制消息格式)进行序列化。 Protobuf 在服务器和客户端上可以非常快速地序列化。 Protobuf 序列化产生的有效负载较小,这在移动应用等带宽有限的方案中很重要。 gRPC 专为 HTTP/2(HTTP…...

vue 导出el-table表格数据
1.先安装 file-saver 、xlsx 组件 npm install file-saver -Snpm intsall xlsx -S 2.html 代码 <el-table :data"elTable" ref"" id"table-content"><el-table-column label"其他" align"center"></el-…...

日语AI面试高效通关秘籍:专业解读与青柚面试智能助攻
在如今就业市场竞争日益激烈的背景下,越来越多的求职者将目光投向了日本及中日双语岗位。但是,一场日语面试往往让许多人感到步履维艰。你是否也曾因为面试官抛出的“刁钻问题”而心生畏惧?面对生疏的日语交流环境,即便提前恶补了…...

装饰模式(Decorator Pattern)重构java邮件发奖系统实战
前言 现在我们有个如下的需求,设计一个邮件发奖的小系统, 需求 1.数据验证 → 2. 敏感信息加密 → 3. 日志记录 → 4. 实际发送邮件 装饰器模式(Decorator Pattern)允许向一个现有的对象添加新的功能,同时又不改变其…...

JVM垃圾回收机制全解析
Java虚拟机(JVM)中的垃圾收集器(Garbage Collector,简称GC)是用于自动管理内存的机制。它负责识别和清除不再被程序使用的对象,从而释放内存空间,避免内存泄漏和内存溢出等问题。垃圾收集器在Ja…...

2025 后端自学UNIAPP【项目实战:旅游项目】6、我的收藏页面
代码框架视图 1、先添加一个获取收藏景点的列表请求 【在文件my_api.js文件中添加】 // 引入公共的请求封装 import http from ./my_http.js// 登录接口(适配服务端返回 Token) export const login async (code, avatar) > {const res await http…...

LLM基础1_语言模型如何处理文本
基于GitHub项目:https://github.com/datawhalechina/llms-from-scratch-cn 工具介绍 tiktoken:OpenAI开发的专业"分词器" torch:Facebook开发的强力计算引擎,相当于超级计算器 理解词嵌入:给词语画"…...

MySQL 知识小结(一)
一、my.cnf配置详解 我们知道安装MySQL有两种方式来安装咱们的MySQL数据库,分别是二进制安装编译数据库或者使用三方yum来进行安装,第三方yum的安装相对于二进制压缩包的安装更快捷,但是文件存放起来数据比较冗余,用二进制能够更好管理咱们M…...

【从零学习JVM|第三篇】类的生命周期(高频面试题)
前言: 在Java编程中,类的生命周期是指类从被加载到内存中开始,到被卸载出内存为止的整个过程。了解类的生命周期对于理解Java程序的运行机制以及性能优化非常重要。本文会深入探寻类的生命周期,让读者对此有深刻印象。 目录 …...

在鸿蒙HarmonyOS 5中使用DevEco Studio实现企业微信功能
1. 开发环境准备 安装DevEco Studio 3.1: 从华为开发者官网下载最新版DevEco Studio安装HarmonyOS 5.0 SDK 项目配置: // module.json5 {"module": {"requestPermissions": [{"name": "ohos.permis…...

Qt的学习(一)
1.什么是Qt Qt特指用来进行桌面应用开发(电脑上写的程序)涉及到的一套技术Qt无法开发网页前端,也不能开发移动应用。 客户端开发的重要任务:编写和用户交互的界面。一般来说和用户交互的界面,有两种典型风格&…...

LUA+Reids实现库存秒杀预扣减 记录流水 以及自己的思考
目录 lua脚本 记录流水 记录流水的作用 流水什么时候删除 我们在做库存扣减的时候,显示基于Lua脚本和Redis实现的预扣减 这样可以在秒杀扣减的时候保证操作的原子性和高效性 lua脚本 // ... 已有代码 ...Overridepublic InventoryResponse decrease(Inventor…...
