无重复字符的最长子串[中等]
优质博文:IT-BLOG-CN

一、题目
给定一个字符串s,请你找出其中不含有重复字符的最长子串的长度。
示例 1:
输入: s = "abcabcbb"
输出: 3
解释: 因为无重复字符的最长子串是"abc",所以其长度为3。
示例 2:
输入: s = "bbbbb"
输出: 1
解释: 因为无重复字符的最长子串是"b",所以其长度为1。
示例 3:
输入: s = "pwwkew"
输出: 3
解释: 因为无重复字符的最长子串是"wke",所以其长度为3。
请注意,你的答案必须是 子串 的长度,
pwke是一个子序列,不是子串。
注意:
0 <= s.length <= 5 * 104
s由英文字母、数字、符号和空格组成
二、代码
方案一
思路:
【1】通过hashMap[key = val , value = index]存放字符串中的字母;
【2】当有重复字母出现时,将left指向重复字母最左边的下标;
【3】最后通过i = left获取下标与left取最大值;
/*** 思路:1、通过hashMap[key = val , value = index]存放字符串中的字母;* 2、当有重复字母出现时,将 left 指向重复字母最左边的下标;* 3、最后通过 i = left 获取下标 与 left取最大值;*/
class Solution {public int lengthOfLongestSubstring(String s) {Map<Character,Integer> map = new HashMap();int left = 0;int max = 0;if (s.length() == 0) return 0;for (int i = 0; i < s.length(); i++) {if (map.containsKey(s.charAt(i))) {left = Math.max(left, map.get(s.charAt(i)) + 1);}map.put(s.charAt(i), i);max = Math.max(max, i - left + 1);}return max;}
}
方案二
思路: 方案一时左指针基本不动,右指针遍历。方案二是左指针遍历,右指针基本不动。
通过HashSet对记录字符串,包含时计算长度,并对右指针进行偏移,如果不包含则偏移左指针。
class Solution {public int lengthOfLongestSubstring(String s) {// 哈希集合,记录每个字符是否出现过Set<Character> occ = new HashSet<Character>();int n = s.length();// 右指针,初始值为 -1,相当于我们在字符串的左边界的左侧,还没有开始移动int rk = -1, ans = 0;for (int i = 0; i < n; ++i) {if (i != 0) {// 左指针向右移动一格,移除一个字符occ.remove(s.charAt(i - 1));}while (rk + 1 < n && !occ.contains(s.charAt(rk + 1))) {// 不断地移动右指针occ.add(s.charAt(rk + 1));++rk;}// 第 i 到 rk 个字符是一个极长的无重复字符子串ans = Math.max(ans, rk - i + 1);}return ans;}
}
复杂度分析: O(N)其中N是字符串的长度。左指针和右指针分别会遍历整个字符串一次。
空间复杂度: O(∣Σ∣)其中Σ表示字符集(即字符串中可以出现的字符),∣Σ∣|表示字符集的大小。在本题中没有明确说明字符集,因此可以默认为所有ASCII码在[0,128)内的字符,即∣Σ∣=128。我们需要用到哈希集合来存储出现过的字符,而字符最多有∣Σ∣个,因此空间复杂度为O(∣Σ∣)
方案三:滑动窗口
我们先用一个例子考虑如何在较优的时间复杂度内通过本题。
我们不妨以示例一中的字符串abcabcbb为例,找出从每一个字符开始的,不包含重复字符的最长子串,那么其中最长的那个字符串即为答案。对于示例一中的字符串,我们列举出这些结果,其中括号中表示选中的字符以及最长的字符串:
以(a)bcabcbb开始的最长字符串为(abc)abcbb;
以a(b)cabcbb开始的最长字符串为a(bca)bcbb;
以ab(c)abcbb开始的最长字符串为ab(cab)cbb;
以abc(a)bcbb开始的最长字符串为abc(abc)bb;
以abca(b)cbb开始的最长字符串为abca(bc)bb;
以abcab(c)bb开始的最长字符串为abcab(cb)b;
以abcabc(b)b开始的最长字符串为abcabc(b)b;
以abcabcb(b)开始的最长字符串为abcabcb(b)。
发现了什么?如果我们依次递增地枚举子串的起始位置,那么子串的结束位置也是递增的!这里的原因在于,假设我们选择字符串中的第k个字符作为起始位置,并且得到了不包含重复字符的最长子串的结束位置为rk。那么当我们选择第k+1个字符作为起始位置时,首先从k+1到rk的字符显然是不重复的,并且由于少了原本的第k个字符,我们可以尝试继续增大rk,直到右侧出现了重复字符为止。
这样一来,我们就可以使用「滑动窗口」来解决这个问题了:
我们使用两个指针表示字符串中的某个子串(或窗口)的左右边界,其中左指针代表着上文中「枚举子串的起始位置」,而右指针即为上文中的rk;
在每一步的操作中,我们会将左指针向右移动一格,表示 我们开始枚举下一个字符作为起始位置,然后我们可以不断地向右移动右指针,但需要保证这两个指针对应的子串中没有重复的字符。在移动结束后,这个子串就对应着 以左指针开始的,不包含重复字符的最长子串。我们记录下这个子串的长度;
在枚举结束后,我们找到的最长的子串的长度即为答案。
**判断重复字符:**在上面的流程中,我们还需要使用一种数据结构来判断 是否有重复的字符,常用的数据结构为哈希集合。在左指针向右移动的时候,我们从哈希集合中移除一个字符,在右指针向右移动的时候,我们往哈希集合中添加一个字符。
class Solution {public int lengthOfLongestSubstring(String s) {// 哈希集合,记录每个字符是否出现过Set<Character> occ = new HashSet<Character>();int n = s.length();// 右指针,初始值为 -1,相当于我们在字符串的左边界的左侧,还没有开始移动int rk = -1, ans = 0;for (int i = 0; i < n; ++i) {if (i != 0) {// 左指针向右移动一格,移除一个字符occ.remove(s.charAt(i - 1));}while (rk + 1 < n && !occ.contains(s.charAt(rk + 1))) {// 不断地移动右指针occ.add(s.charAt(rk + 1));++rk;}// 第 i 到 rk 个字符是一个极长的无重复字符子串ans = Math.max(ans, rk - i + 1);}return ans;}
}
时间复杂度: O(N),其中N是字符串的长度。左指针和右指针分别会遍历整个字符串一次。
空间复杂度: O(∣Σ∣),其中Σ表示字符集(即字符串中可以出现的字符),∣Σ∣表示字符集的大小。在本题中没有明确说明字符集,因此可以默认为所有ASCII码在[0,128)内的字符,即∣Σ∣=128。我们需要用到哈希集合来存储出现过的字符,而字符最多有∣Σ∣个,因此空间复杂度为O(∣Σ∣)。
相关文章:

无重复字符的最长子串[中等]
优质博文:IT-BLOG-CN 一、题目 给定一个字符串s,请你找出其中不含有重复字符的最长子串的长度。 示例 1: 输入: s "abcabcbb" 输出: 3 解释: 因为无重复字符的最长子串是"abc",所以其长度为3。 示例 2: 输入: s &…...

考研经验总结——目录
文章目录 一、写作顺序二、个人情况说明三、读评论四、一些小牢骚五、一些注意事项(持续更新) 一、写作顺序 我将准备从三个阶段开始介绍吧 考研前考研中考研后(也就是现在我的这种情况) 考研前我会分为:数学、专业…...

Docker(一)简介和基本概念
一、简介 本章将带领你进入 Docker 的世界。 什么是 Docker? 用它会带来什么样的好处? 好吧,让我们带着问题开始这神奇之旅。 1.什么是 Docker Docker 最初是 dotCloud 公司创始人 Solomon Hykes 在法国期间发起的一个公司内部项目&…...
openssl3.2 - 官方demo学习 - test - certs
文章目录 openssl3.2 - 官方demo学习 - test - certs概述笔记.sh的执行语句打印的方法要修改的实际函数END openssl3.2 - 官方demo学习 - test - certs 概述 官方demos目录有证书操作的例子 已经做了笔记 openssl3.2 - 官方demo学习 - certs 但是这个demos/certs目录的脚本,…...
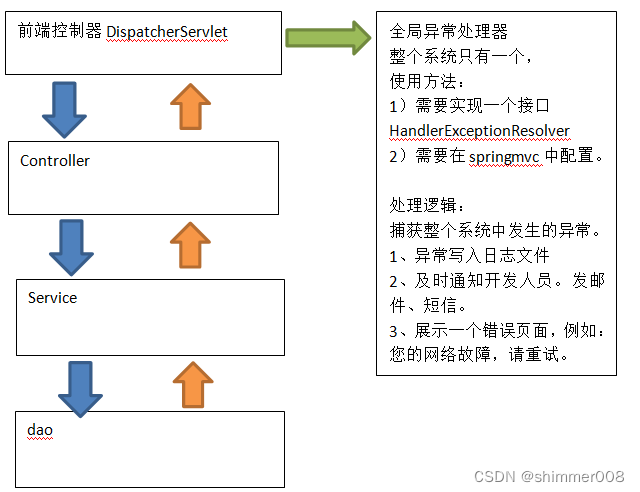
Spring MVC学习之——异常处理器
异常处理器 如果不加以异常处理,错误信息肯定会抛在浏览器页面上,这样很不友好,所以必须进行异常处理。 1.异常处理思路 系统的dao、service、controller出现都通过throws Exception向上抛出,最后由springmvc前端控制器交由异常…...
:HMAC Authentication)
HTTP API 认证技术详解(四):HMAC Authentication
目录 什么是 HMAC Authentication 认证 HMAC Authentication 原理 HMAC Authentication 认证的步骤 使用 Golang 实现 HMAC Authentication 认证 HMAC Authentication 认证的安全性 HMAC 认证的最佳实践 小结 HTTP API 认证技术主要用于验证客户端身份,并确保…...
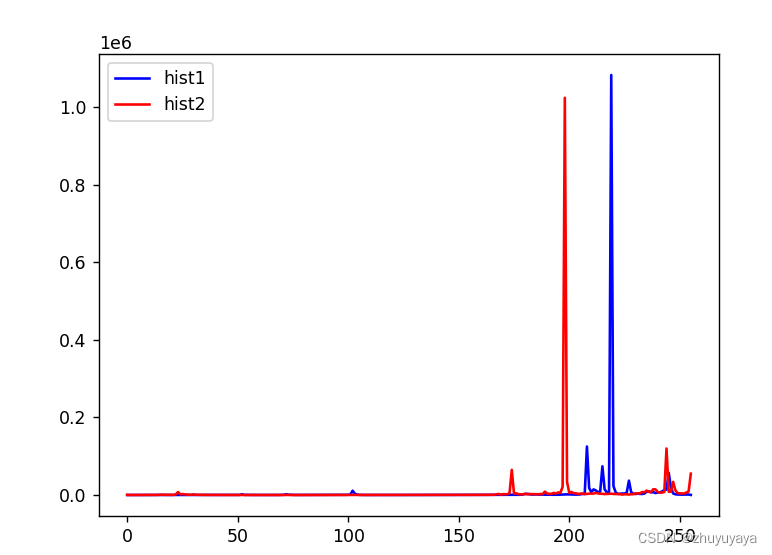
如何绘制出图像的色素分布直方图
效果 如图,可以展示出我们的图像的颜色分布直方图,表明的图像的亮和暗 实现可视化色素分布直方图方法 这里我们对我们的灰色图片和彩色图片进行了直方图显示 import cv2 import matplotlib.pyplot as plt image cv2.imread("test.jpg") # 彩色图片->…...

esp32-c-简单应用笔记
1、资料 ESP32 开发环境 Espressif-IDE: https://blog.csdn.net/chuner0425/article/details/123466848 https://blog.csdn.net/bin_zhang1/article/details/129993820?utm_mediumdistribute.pc_relevant.none-task-blog-2defaultbaidujs_baidulandingword~default-0-1299938…...

What is `XSS` does?
跨站脚本攻击(Cross-Site Scripting,XSS)是一种针对网站应用程序的安全漏洞,允许攻击者将恶意脚本注入到其他用户查看的网页中。当这些用户访问受感染的页面时,他们的浏览器会执行这些恶意脚本,导致各种安全…...
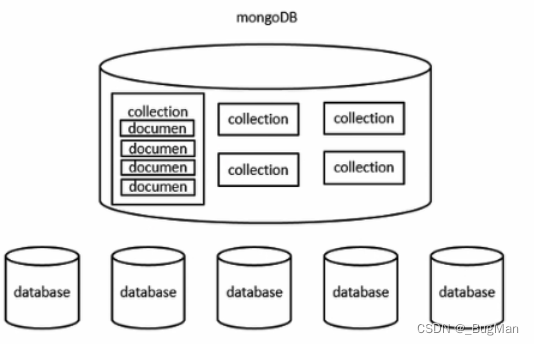
【文档数据库】ES和MongoDB的对比
目录 1.由文档存储牵出的问题 2.什么是MongoDB? 3.ES和MongoDB的对比 1.由文档存储牵出的问题 本文或者说关于mongodb的这个系列文章的源头: 前面我们聊过了分布式链路追踪系统,在基于日志实现的分布式链路追踪的方式seluthzipkin中为了…...

VUE工程化项目--vue组件化
组件化开发 & 根组件 : ① 组件化: 一个页面可以拆分成 一个个组件 ,每个组件有着自己独立的 结构、样式、行为 。 好处:便于 维护 ,利于 复用 → 提升 开发效率 。 组件分类:普通组件、根组件。 …...

iOS base64 转 data |图片Base64转NSData | UIImageView | UIImage
Api 接口返回 base64 图片字符串,需要显示在UIImageView 上。 假设 string类型的 base64ImageStr 为 api返回的 base64字符串 将base64字符串进行处理 //去除掉首尾的空白字符和换行字符NSString * img64 [img stringByTrimmingCharactersInSet:[NSCharacterSet …...

Unity面试笔记:Unity常见关键词概念
Unity面试笔记:Unity常见关键词概念 Invoke 延迟函数 和 Coroutine协程 和 Thread线程帧缓冲区(Frame buffer)颜色缓冲区(Color buffer)深度缓冲区(Depth buffer)模板缓冲区(Stencil…...

gRPC vs HTTP
性能 gRPC 消息使用 Protobuf(一种高效的二进制消息格式)进行序列化。 Protobuf 在服务器和客户端上可以非常快速地序列化。 Protobuf 序列化产生的有效负载较小,这在移动应用等带宽有限的方案中很重要。 gRPC 专为 HTTP/2(HTTP…...

vue 导出el-table表格数据
1.先安装 file-saver 、xlsx 组件 npm install file-saver -Snpm intsall xlsx -S 2.html 代码 <el-table :data"elTable" ref"" id"table-content"><el-table-column label"其他" align"center"></el-…...

【问题记录】AttributeError: module ‘numpy‘ has no attribute ‘bool‘
服务器上运行代码报错: /opt/conda/envs/clrnet/lib/python3.8/site-packages/imgaug-0.4.0-py3.8.egg/imgaug/augmenters/meta.py:3368: FutureWarning: In the future np.bool will be defined as the corresponding NumPy scalar. augmenter_active np.zeros((n…...

WordPress企业模板
首页大图wordpress外贸企业模板 橙色的wordpress企业模板 演示 https://www.zhanyes.com/waimao/6250.html...
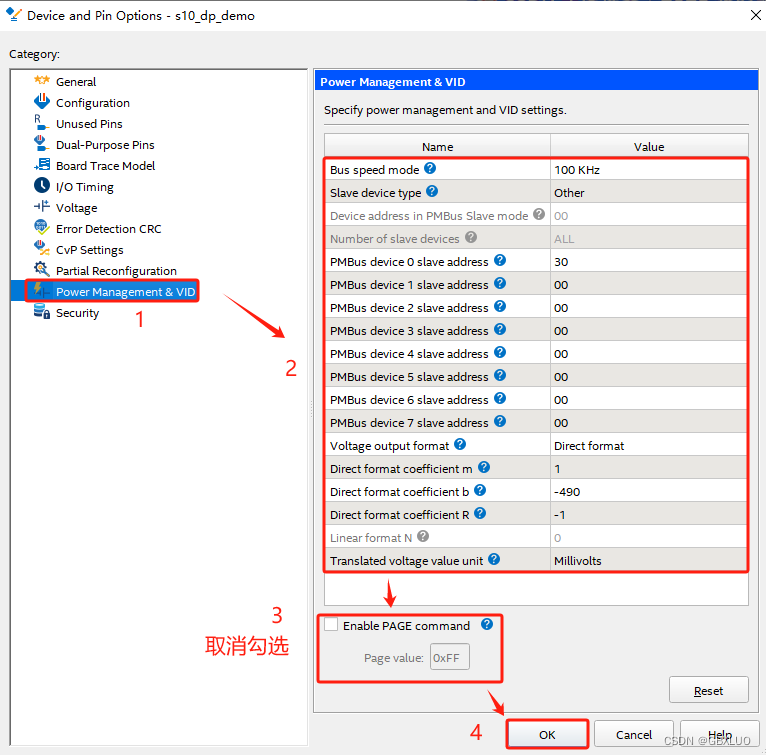
Intel Quartus II IP之DP1.4 工程的创建与使用
前述: Win10电脑安装了Quartus 21.4,这可以满足绝大多数工程,特别是对于简单调用fifo/ram等的工程,但是想要学习Quartus的HDMI/DP等高速接口类IP,首先需要创建HDMI/DP IP的设计demo工程,此时还需要安装Ecl…...
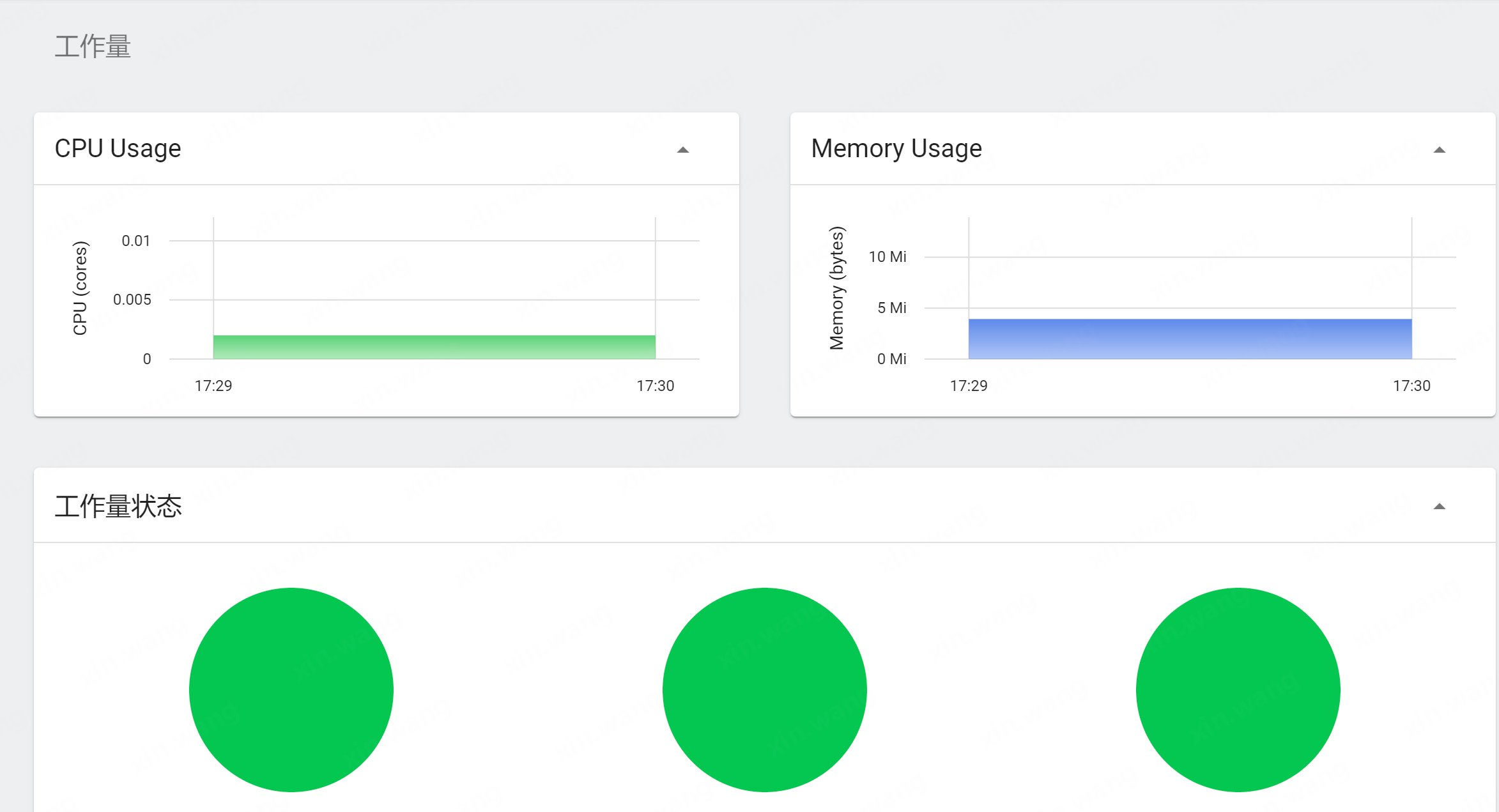
k8s集群环境搭建以及插件安装
前置条件 终端工具MobaXterm很好用。 1、虚拟机三台(ip按自己的网络环境相应配置)(master/node) 节点ipk8s-master192.168.200.150k8s-node1192.168.200.151k8s-node2192.168.200.152 2、关闭防火墙(master/node) systemctl stop firewalld systemc…...

面试的那些事儿
先从面试来说 假如你是网申,你的简历必然会经过HR的筛选,一张简历HR可能也就花费10秒钟看一下,然后HR 就会决定你这一关是Fail还是Pass。 假如你是内推,如果你的简历没有什么优势的话,就算是内推你的人再用心&#x…...

19c补丁后oracle属主变化,导致不能识别磁盘组
补丁后服务器重启,数据库再次无法启动 ORA01017: invalid username/password; logon denied Oracle 19c 在打上 19.23 或以上补丁版本后,存在与用户组权限相关的问题。具体表现为,Oracle 实例的运行用户(oracle)和集…...

【人工智能】神经网络的优化器optimizer(二):Adagrad自适应学习率优化器
一.自适应梯度算法Adagrad概述 Adagrad(Adaptive Gradient Algorithm)是一种自适应学习率的优化算法,由Duchi等人在2011年提出。其核心思想是针对不同参数自动调整学习率,适合处理稀疏数据和不同参数梯度差异较大的场景。Adagrad通…...

【Linux】C语言执行shell指令
在C语言中执行Shell指令 在C语言中,有几种方法可以执行Shell指令: 1. 使用system()函数 这是最简单的方法,包含在stdlib.h头文件中: #include <stdlib.h>int main() {system("ls -l"); // 执行ls -l命令retu…...

Java如何权衡是使用无序的数组还是有序的数组
在 Java 中,选择有序数组还是无序数组取决于具体场景的性能需求与操作特点。以下是关键权衡因素及决策指南: ⚖️ 核心权衡维度 维度有序数组无序数组查询性能二分查找 O(log n) ✅线性扫描 O(n) ❌插入/删除需移位维护顺序 O(n) ❌直接操作尾部 O(1) ✅内存开销与无序数组相…...

【快手拥抱开源】通过快手团队开源的 KwaiCoder-AutoThink-preview 解锁大语言模型的潜力
引言: 在人工智能快速发展的浪潮中,快手Kwaipilot团队推出的 KwaiCoder-AutoThink-preview 具有里程碑意义——这是首个公开的AutoThink大语言模型(LLM)。该模型代表着该领域的重大突破,通过独特方式融合思考与非思考…...

1.3 VSCode安装与环境配置
进入网址Visual Studio Code - Code Editing. Redefined下载.deb文件,然后打开终端,进入下载文件夹,键入命令 sudo dpkg -i code_1.100.3-1748872405_amd64.deb 在终端键入命令code即启动vscode 需要安装插件列表 1.Chinese简化 2.ros …...

rnn判断string中第一次出现a的下标
# coding:utf8 import torch import torch.nn as nn import numpy as np import random import json""" 基于pytorch的网络编写 实现一个RNN网络完成多分类任务 判断字符 a 第一次出现在字符串中的位置 """class TorchModel(nn.Module):def __in…...

HarmonyOS运动开发:如何用mpchart绘制运动配速图表
##鸿蒙核心技术##运动开发##Sensor Service Kit(传感器服务)# 前言 在运动类应用中,运动数据的可视化是提升用户体验的重要环节。通过直观的图表展示运动过程中的关键数据,如配速、距离、卡路里消耗等,用户可以更清晰…...
)
GitHub 趋势日报 (2025年06月06日)
📊 由 TrendForge 系统生成 | 🌐 https://trendforge.devlive.org/ 🌐 本日报中的项目描述已自动翻译为中文 📈 今日获星趋势图 今日获星趋势图 590 cognee 551 onlook 399 project-based-learning 348 build-your-own-x 320 ne…...

【Linux手册】探秘系统世界:从用户交互到硬件底层的全链路工作之旅
目录 前言 操作系统与驱动程序 是什么,为什么 怎么做 system call 用户操作接口 总结 前言 日常生活中,我们在使用电子设备时,我们所输入执行的每一条指令最终大多都会作用到硬件上,比如下载一款软件最终会下载到硬盘上&am…...
