1125. 牛的旅行 (Floyd算法,最短路)
1125. 牛的旅行 - AcWing题库
农民John的农场里有很多牧区,有的路径连接一些特定的牧区。
一片所有连通的牧区称为一个牧场。
但是就目前而言,你能看到至少有两个牧区不连通。
现在,John想在农场里添加一条路径(注意,恰好一条)。
一个牧场的直径就是牧场中最远的两个牧区的距离(本题中所提到的所有距离指的都是最短的距离)。
考虑如下的两个牧场,每一个牧区都有自己的坐标:
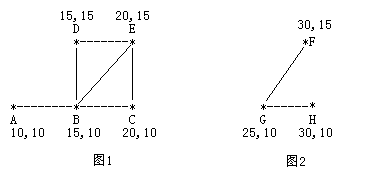
图 1 是有 5 个牧区的牧场,牧区用“*”表示,路径用直线表示。
图 1 所示的牧场的直径大约是 12.07106, 最远的两个牧区是 A 和 E,它们之间的最短路径是 A-B-E。
图 2 是另一个牧场。
这两个牧场都在John的农场上。
John将会在两个牧场中各选一个牧区,然后用一条路径连起来,使得连通后这个新的更大的牧场有最小的直径。
注意,如果两条路径中途相交,我们不认为它们是连通的。
只有两条路径在同一个牧区相交,我们才认为它们是连通的。
现在请你编程找出一条连接两个不同牧场的路径,使得连上这条路径后,所有牧场(生成的新牧场和原有牧场)中直径最大的牧场的直径尽可能小。
输出这个直径最小可能值。
输入格式
第 1 行:一个整数 N, 表示牧区数;
第 2 到 N+1 行:每行两个整数 X,Y, 表示 N 个牧区的坐标。每个牧区的坐标都是不一样的。
第 N+2 行到第 2*N+1 行:每行包括 N 个数字 ( 0或1 ) 表示一个对称邻接矩阵。
例如,题目描述中的两个牧场的矩阵描述如下:
A B C D E F G H
A 0 1 0 0 0 0 0 0
B 1 0 1 1 1 0 0 0
C 0 1 0 0 1 0 0 0
D 0 1 0 0 1 0 0 0
E 0 1 1 1 0 0 0 0
F 0 0 0 0 0 0 1 0
G 0 0 0 0 0 1 0 1
H 0 0 0 0 0 0 1 0
输入数据中至少包括两个不连通的牧区。
输出格式
只有一行,包括一个实数,表示所求答案。
数字保留六位小数。
数据范围
1≤N≤150
0≤X,Y≤105
输入样例:
8
10 10
15 10
20 10
15 15
20 15
30 15
25 10
30 10
01000000
10111000
01001000
01001000
01110000
00000010
00000101
00000010
输出样例:
22.071068解析:
1.答案大于等于所有连通块直径的最大值
2.经过新边的最长的最短路径
具体过程:
1.用floyd算法求出任意两点之间的最短距离
2.求出max[i],表示和i连通的且距离i最远的点的距离
3.情况1:所有max[i]的最大值
情况2:枚举在哪两个点之间连边。i,j,需要满足d[i,j]=INF, maxd[i]+dist[i,j]+maxd[j]
#include<iostream>
#include<string>
#include<cstring>
#include<cmath>
#include<ctime>
#include<algorithm>
#include<utility>
#include<stack>
#include<queue>
#include<vector>
#include<set>
#include<math.h>
#include<map>
#include<sstream>
#include<deque>
#include<unordered_map>
using namespace std;
const int N = 150 + 5;
const double INF = 1e20;
int n;
char g[N][N];
double d[N][N],maxd[N];
typedef pair<double, double> PII;
PII p[N];double get_dist(PII a, PII b) {double dx = a.first - b.first;double dy = a.second - b.second;return sqrt(dx * dx + dy * dy);
}int main() {cin >> n;for (int i = 1; i <= n; i++) {scanf("%lf%lf", &p[i].first, &p[i].second);}for (int i = 1; i <= n; i++) {scanf("%s", g[i] + 1);}for (int i = 1; i <= n; i++) {for (int j = 1; j <= n; j++) {if (g[i][j] == '1')d[i][j] = get_dist(p[i], p[j]);else if (i == j)d[i][j] = 0;else d[i][j] = INF;}}for (int k = 1; k <= n; k++) {for (int i = 1; i <= n; i++) {for (int j = 1; j <= n; j++) {d[i][j] = min(d[i][j], d[i][k] + d[k][j]);}}}for (int i = 1; i <= n; i++) {for (int j = 1; j <= n; j++) {if (d[i][j] < INF / 2)maxd[i] = max(maxd[i], d[i][j]);}}double ret1 = 0;for (int i = 1; i <= n; i++) {ret1 = max(ret1, maxd[i]);}double ret2 = INF;for (int i = 1; i <= n; i++) {for (int j = 1; j <= n; j++) {if(d[i][j]>INF/2)ret2 = min(ret2, maxd[i] + maxd[j] + get_dist(p[i], p[j]));}}printf("%.6lf\n", max(ret1, ret2));return 0;
}相关文章:
1125. 牛的旅行 (Floyd算法,最短路)
1125. 牛的旅行 - AcWing题库 农民John的农场里有很多牧区,有的路径连接一些特定的牧区。 一片所有连通的牧区称为一个牧场。 但是就目前而言,你能看到至少有两个牧区不连通。 现在,John想在农场里添加一条路径(注意ÿ…...
的概念)
oracle “Interested Transaction List”(ITL)的概念
“Interested Transaction List”(ITL)的概念。让我们逐点理解: 块头和ITL: 每个数据库段块的块头都包含一个Interested Transaction List(ITL)。ITL用于确定数据库开始修改块时某个事务是否未提交。 ITL的…...

kali下-MSF-ftp_login模块破解FTP账号及密码
一、环境准备 两台设备在同一个网络内 一台kali系统:192.168.10.128 一台winserver2016:192.168.10.132 二、MSF介绍 metasploit 全称是The Metasploit Framework,又称MSF,是Kali 内置的一款渗透测试框架,也是全球…...
ELK之Filebeat输出日志格式设置及输出字段过滤和修改
一、Filebeat输出日志格式设置 1.1 编辑vim filebeat.yml文件,修改输出格式设置 # output to console output.console:codec.format: string: %{[@timestamp]} %{[message]}pretty: true### 1.2 测试 执行 ./filebeat -e 可以看到/tmp/access.log(目前文件里只有140.77.188…...

【开源】基于JAVA的河南软件客服系统
目录 一、摘要1.1 项目介绍1.2 项目录屏 二、功能模块2.1 系统管理人员2.2 业务操作人员 三、系统展示四、核心代码4.1 查询客户4.2 新增客户跟进情况4.3 查询客户历史4.4 新增服务派单4.5 新增客户服务费 五、免责说明 一、摘要 1.1 项目介绍 基于JAVAVueSpringBootMySQL的河…...
基于SpringBoot的社区帮扶对象管理系统
文章目录 项目介绍主要功能截图:部分代码展示设计总结项目获取方式 🍅 作者主页:超级无敌暴龙战士塔塔开 🍅 简介:Java领域优质创作者🏆、 简历模板、学习资料、面试题库【关注我,都给你】 &…...
uniapp踩坑之项目:canvas第一次保存是空白图片
在ctx.draw()回调生成图片,参考canvasToTempFilePath接口文档 // data imgFilePath: null,// 缓存二维码图片canvas路径//js // 首先在draw()里进行本地存储 ...... ctx.draw(false, () >{uni.canvasToTempFilePath({ // 把画布转化成临时…...

es-删除字段-实测
es字段一旦创建是无法删除的,本案的方案是复制新老索引的方法 一、背景 现有索引 index1,待删除字段field1和extendMap.field2,es版本6.3.2 二、步骤 1、删除index1中的filed1和extendMap.field2两个字段的数据 POST index1/_update_by_query {&qu…...

24秋招,百度测试开发工程师三面
前言 大家好,我是chowley,今天来回顾一下,我当时参加百度秋招补录,测试开发工程师的第三面-leader面 到面试开始的时间,面试官打电话表示让我等十分钟,随后跳过自我介绍,直接开面 时间&#…...
)
YOLOv8改进 | 主干篇 | 低照度增强网络PE-YOLO改进主干(改进暗光条件下的物体检测模型)
一、本文介绍 本文给大家带来的改进机制是低照度图像增强网络PE-YOLO中的PENet,PENet通过拉普拉斯金字塔将图像分解成多个分辨率的组件,增强图像细节和低频信息。它包括一个细节处理模块(DPM),用于通过上下文分支和边缘分支增强图像细节,以及一个低频增强滤波器(LEF),…...

【VUE】记录一次 VUE中配置生产环境和开发环境方法
前言 我这里 使用Vue CLI(Vue Command Line Interface)创建Vue.js项目是一种简单的方式,它提供了一个交互式的命令行工具来帮助你初始化和管理Vue.js项目。 并且我这个项目需要区分生产环境和开发环境。这里具体完整记录下,整个…...
tessreact训练字库
tessreact主要用于字符识别,除了使用软件自带的中英文识别库,还可以使用Tesseract OCR训练属于自己的字库。 一、软件环境搭建 使用Tesseract OCR训练自己的字库,需要安装Tesseract OCR和jTessBoxEditor(配套训练工具)。jTessBoxEditor需要…...
)
超时配置(OpenFeign)
默认值 连接超时,默认2s读取超时,默认5s单位: 毫秒 全局配置 package com.learning.springcloud.order.feign.config;import feign.Contract; import feign.Logger; import feign.Request; import org.springframework.context.annotation…...
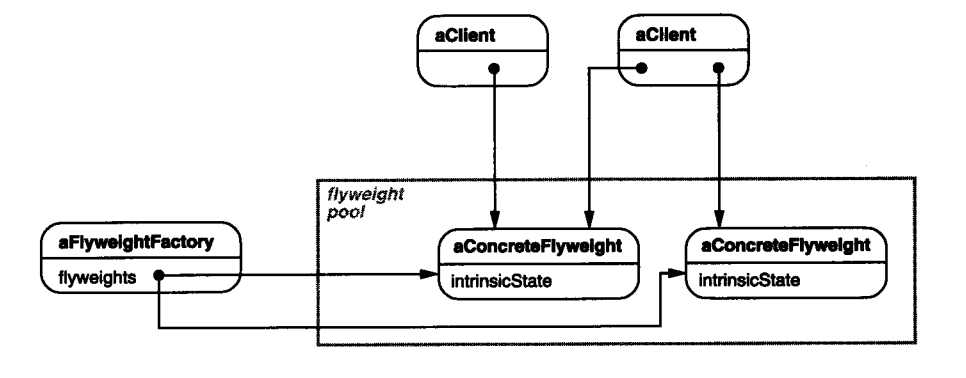
C++设计模式(李建忠)笔记2
C设计模式(李建忠) 本文是学习笔记,如有侵权,请联系删除。 参考链接 Youtube: C设计模式 Gtihub源码与PPT:https://github.com/ZachL1/Bilibili-plus 豆瓣: 设计模式–可复用面向对象软件的基础 文章目录 C设计模…...

【机器学习】DBSCAN算法
参考链接: https://blog.csdn.net/haveanybody/article/details/113092851 https://www.jianshu.com/p/dd6ce77bfb8a 1 介绍 DBSCAN(Density-Based Spatial Clustering of Applica tion with Noise)算法是于1996年提出的一种简单的、有效的基于密度的聚类算法&…...
Uniapp软件库源码-全新带勋章等
测试环境:php7.1。ng1.2,MySQL 5.6 常见问题: 配置好登录后转圈圈,检查环境及伪静态以及后台创建好应用 上传图片不了,检查php拓展fileinfo 以及public文件权限 App个人主页随机背景图,在前端uitl文件夹里面…...

Microsoft Excel 直方图
Microsoft Excel 直方图 1. 数据示例2. 打开 EXCEL3. settings4. 单击直方图柱,右键“添加数据标签”References 1. 数据示例 2. 打开 EXCEL 数据 -> 数据分析 -> 直方图 3. settings 输入区域样本值、接受区域分类间距,输出选项选择“新工作表组…...
如何录制屏幕视频?让视频制作更简单!
随着数字化时代的来临,录制屏幕视频成为一种常见的传播和教学方式。无论是制作演示文稿、教学视频,还是记录游戏操作,屏幕录制为用户提供了强大而灵活的工具。可是您知道如何录制屏幕视频吗?本文将深入介绍两种常见的屏幕录制方法…...

【JavaEE进阶】 关于应用分层
文章目录 🎋序言🍃什么是应⽤分层🎍为什么需要应⽤分层🍀如何分层(三层架构)🎄MVC和三层架构的区别和联系🌳什么是高内聚低耦合⭕总结 🎋序言 在我们进行项目开发时我们如果一股脑将所有代码都…...
【已解决】c语言const/指针学习笔记
本博文源于笔者正在复习const在左与在右,指针优先级、a,&a,*a的区别。 1、const在左与在右 int const *p const int *p int * const p int const * const p const int * const p* 在const右边,指向的数据不可以改变,可以改变地址 * 在c…...

突破不可导策略的训练难题:零阶优化与强化学习的深度嵌合
强化学习(Reinforcement Learning, RL)是工业领域智能控制的重要方法。它的基本原理是将最优控制问题建模为马尔可夫决策过程,然后使用强化学习的Actor-Critic机制(中文译作“知行互动”机制),逐步迭代求解…...

Golang 面试经典题:map 的 key 可以是什么类型?哪些不可以?
Golang 面试经典题:map 的 key 可以是什么类型?哪些不可以? 在 Golang 的面试中,map 类型的使用是一个常见的考点,其中对 key 类型的合法性 是一道常被提及的基础却很容易被忽视的问题。本文将带你深入理解 Golang 中…...

shell脚本--常见案例
1、自动备份文件或目录 2、批量重命名文件 3、查找并删除指定名称的文件: 4、批量删除文件 5、查找并替换文件内容 6、批量创建文件 7、创建文件夹并移动文件 8、在文件夹中查找文件...

什么是库存周转?如何用进销存系统提高库存周转率?
你可能听说过这样一句话: “利润不是赚出来的,是管出来的。” 尤其是在制造业、批发零售、电商这类“货堆成山”的行业,很多企业看着销售不错,账上却没钱、利润也不见了,一翻库存才发现: 一堆卖不动的旧货…...

屋顶变身“发电站” ,中天合创屋面分布式光伏发电项目顺利并网!
5月28日,中天合创屋面分布式光伏发电项目顺利并网发电,该项目位于内蒙古自治区鄂尔多斯市乌审旗,项目利用中天合创聚乙烯、聚丙烯仓库屋面作为场地建设光伏电站,总装机容量为9.96MWp。 项目投运后,每年可节约标煤3670…...

Rust 异步编程
Rust 异步编程 引言 Rust 是一种系统编程语言,以其高性能、安全性以及零成本抽象而著称。在多核处理器成为主流的今天,异步编程成为了一种提高应用性能、优化资源利用的有效手段。本文将深入探讨 Rust 异步编程的核心概念、常用库以及最佳实践。 异步编程基础 什么是异步…...

Pinocchio 库详解及其在足式机器人上的应用
Pinocchio 库详解及其在足式机器人上的应用 Pinocchio (Pinocchio is not only a nose) 是一个开源的 C 库,专门用于快速计算机器人模型的正向运动学、逆向运动学、雅可比矩阵、动力学和动力学导数。它主要关注效率和准确性,并提供了一个通用的框架&…...

python报错No module named ‘tensorflow.keras‘
是由于不同版本的tensorflow下的keras所在的路径不同,结合所安装的tensorflow的目录结构修改from语句即可。 原语句: from tensorflow.keras.layers import Conv1D, MaxPooling1D, LSTM, Dense 修改后: from tensorflow.python.keras.lay…...

Mysql8 忘记密码重置,以及问题解决
1.使用免密登录 找到配置MySQL文件,我的文件路径是/etc/mysql/my.cnf,有的人的是/etc/mysql/mysql.cnf 在里最后加入 skip-grant-tables重启MySQL服务 service mysql restartShutting down MySQL… SUCCESS! Starting MySQL… SUCCESS! 重启成功 2.登…...

Python Einops库:深度学习中的张量操作革命
Einops(爱因斯坦操作库)就像给张量操作戴上了一副"语义眼镜"——让你用人类能理解的方式告诉计算机如何操作多维数组。这个基于爱因斯坦求和约定的库,用类似自然语言的表达式替代了晦涩的API调用,彻底改变了深度学习工程…...
