SpringBoot 读取自定义Properties参数
目录
1. 概述
2. 实现方式
2.1 @Value方式
2.2 @PropertySource与@ConfigurationProperties相结合
3. 结束
1. 概述
最近想尝试写一个定时任务管理,相关参数不想在Spring的配置文件Application.yml或者Application.properties获取。想自己新建一个properties文件。顺便对参数读取进行学习总结。
2. 实现方式
2.1 @Value方式
该方式可以从Application.properties或者Application.yml获取
在文件中可以自定义参数,比如这样:
获取写成这样:

2.2 @PropertySource与@ConfigurationProperties相结合
pfrefix="syjk" 表示参数带有前缀"syjk"
我将参数写在info.properties下
syjk.loginurl=url1
syjk.uploadurl=url2
syjk.username=102020
syjk.password=365241
syjk.realtime=5然后定义一个Bean类,
@Data
@Component
@PropertySource(value = "classpath:info.properties")
@ConfigurationProperties(prefix = "syjk")
public class Info {private String loginurl; //授权地址private String uploadurl; //上传地址private String username; //账号private String password; //密码private int realtime; //定时间隔
}方便看效果,我在controller中来测试下:
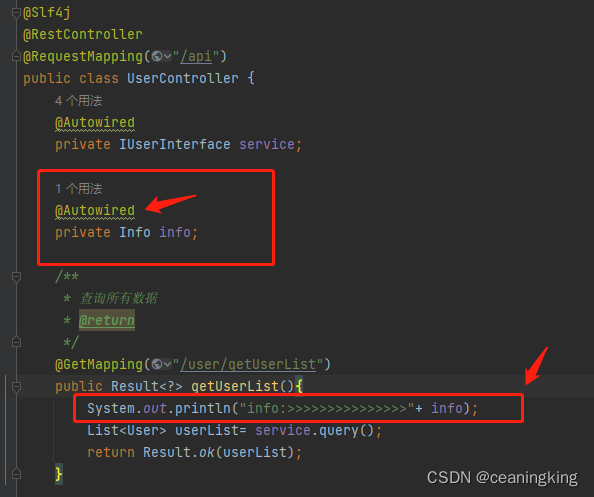
调用getUserList接口,后台显示与info.properties设置一致

3. 结束
学习总结.
相关文章:

SpringBoot 读取自定义Properties参数
目录 1. 概述 2. 实现方式 2.1 Value方式 2.2 PropertySource与ConfigurationProperties相结合 3. 结束 1. 概述 最近想尝试写一个定时任务管理,相关参数不想在Spring的配置文件Application.yml或者Application.properties获取。想自己新建一个properties文件。顺…...
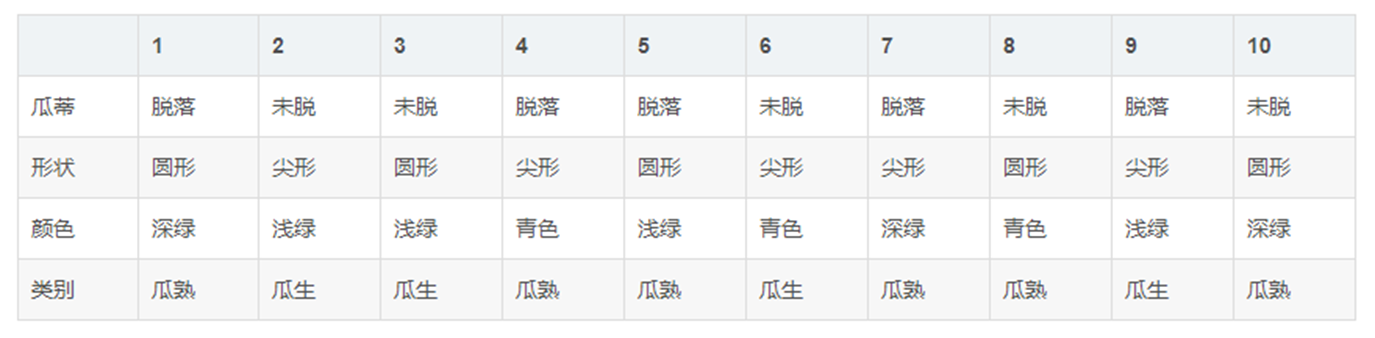
机器学习100天(三十七):037 朴素贝叶斯-挑个好西瓜!
《机器学习100天》完整目录:目录 机器学习100天,今天讲的是:朴素贝叶斯-挑个好西瓜! 红色石头已经了解了贝叶斯定理和朴素贝叶斯法,接下来已经可以很自信地去买瓜了。买瓜之前,还有一件事情要做,就是搜集样本数据。红色石头通过网上资料和查阅,获得了一组包含 10 组样…...

c#遍历窗口,根据标题获取handle并显示窗口
using System.Runtime.InteropServices;using System.Text;//1,定义//[DllImport("User32.dll", EntryPoint "FindWindow")]//public extern static IntPtr FindWindow(string lpClassName, string lpWindowName);[DllImport("user32.dll…...
MyBatis高频面试专题
一、介绍下MyBatis中的工作原理 1。介绍MyBatis的基本情况:ORM 2。原理: MyBatis框架的初始化操作处理SQL请求的流程 1.系统启动的时候会加载解析全局配置文件和对应映射文件。加载解析的相关信息存储在 Configuration 对象 Testpublic void test1(…...

曹云金郭德纲关系迎曙光,新剧《猎黑行动》被德云社弟子齐点赞
话说天下大势,分久必合,合久必分。这句话经过了历史的证明,如今依然感觉非常实用。 就拿郭德纲和曹云金来说,曾经后者是前者的得门生,两个人不但情同父子,曹云金还是郭德纲默认接班人。然而随着时间的流逝&…...

如何在 OpenEuler 系统中安装 Docker
Docker 是一种流行的开源容器化平台,它能够将应用程序与其依赖项打包成可移植的容器,从而简化了应用程序的部署和管理。本文将介绍在 OpenEuler 系统中安装 Docker 并使用 Docker 容器控制 5G 模块的具体步骤。 安装 Docker 安装 Docker 的具体步骤如下…...
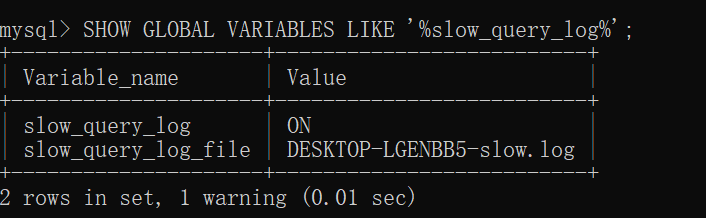
MySQL日志管理
日志管理在数据库保存数据时,有时候不可避免会出现数据丢失或者被破坏,这种时候,我们必须保证数据的安全性和完整性,就需要使用日志来查看或者恢复数据了数据库中数据丢失或被破坏可能原因:误删除数据库数据库工作时&a…...

进 制
进制进制一、进制概念二、进制的转换三、二进制的运算3.1 与运算3.2 或运算3.3 非运算3.4 异或运算3.5 位运算(位移)四、原码、反码、补码4.1 原码4.2 反码4.3 补码五、浮点数十进制转换成二进制进制 一、进制概念 十进制是指逢十进一。 计算机中二进制…...
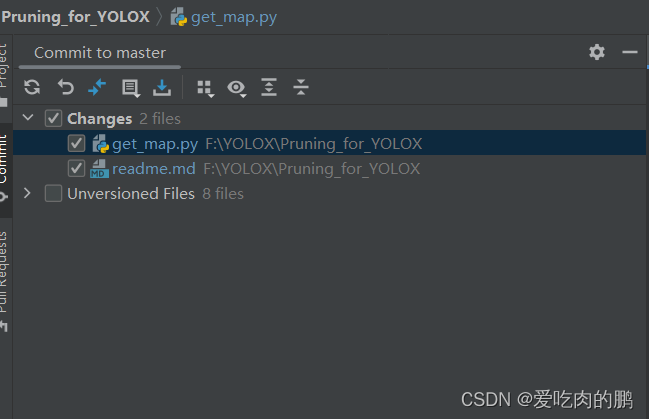
pycharm关联github、新建以及更新仓
此处已经默认你安装了git以及pycharm,这篇文章将会教给大家如何利用pycharm管理自己的github. 目录 pycharm关联github设置 Github创建新的仓 仓库的更新 pycharm:2022。不同版本界面略有不同。 pycharm关联github设置 设置PyCharm,打开File --> Settings -…...
---嘻嘻,春招加油呀~)
java基础知识之小碎片(自问自答版本)---嘻嘻,春招加油呀~
1.public/private/protected/default的区别? public:对所有类可见 private 只有类本身可以访问,其他类想访问可以通过该类的成员方法访问如getter/setter protected:对同一包内的类和所有子类可见 default:在同一包内可见,不加修饰符 2.jav…...

蚁群算法c++
//轮盘赌选择下一步行进城市 int citySelect(int k, int f) { int c 0;//记录蚂蚁可行进的城市个数 //1、计算可行进的各城市 选择概率 for (int m 0; m < cityNum; m) { //若城市(i,j)之间有路且j不在蚂蚁k的禁忌表中…...

北大青鸟天府校区IT学习大揭秘
口罩已放开,一切都要重新出发。 开年才一个多月,已经有很多小伙伴想培训转行IT行业或者已经在咨询、报名培训IT技术。作为老牌培训机构,也有很多小伙伴相信我们,选择了我们。很感谢大家的信任,作为老牌培训机构&#…...

04 Linux errno.h错误码中文注释
Linux错误码中文注释 作者将狼才鲸创建日期2023-03-04/******************************************************************************* \brief 错误码* \note 基于linux_6.1-rc4\include\uapi\asm-generic\errno-base.h* linux_6.1-rc4\tools\arch\alpha\include\uapi…...

MySQL表的约束
文章目录表的约束空属性默认值列描述zerofill主键自增长唯一键外键表的约束 真正约束字段的是数据类型,但是数据类型约束很单一,需要有一些额外的约束,更好的保证数据的合法性,从业务逻辑角度保证数据的正确性。比如说我们的居民…...

Go语言的条件控制语句及循环语句的学习笔记
一、Go的条件控制语句 Go 语言提供了以下几种条件判断语句: 语句描述if 语句if 语句 由一个布尔表达式后紧跟一个或多个语句组成。if…else 语句if 语句 后可以使用可选的 else 语句, else 语句中的表达式在布尔表达式为 false 时执行。if 嵌套语句你可以在 if 或…...

D. Linguistics(思维 + 贪心)
Problem - D - Codeforces Alina发现了一种奇怪的语言,它只有4个单词:a, B, AB, BA。事实也证明,在这种语言中没有空格:一个句子是通过将单词连接成一个字符串来写的。Alina发现了一个这样的句子,她很好奇:有没有可能它恰好由a个单词a, b个单…...

maxWell数据迁移
目录 1.开启mysql的binlog 1.1: Statement-based 1.2: Row-based 1.3: mixed 2. 重启mysql服务 3. 创建Maxwell所需数据库和用户 4. 配置Maxwell 5. Maxwell启停(实时同步) 6. 历史数据全量同步 这里使用maxWell对mysql数据迁移到kafka中 官网下载地址点击下载 注&#x…...

混合图像python旗舰版
仔细看这个图像。然后后退几米再看。你看到了什么?混合图像是指将一张图片的低频与另一张图片的高频相结合的图片。根据观看距离的不同,所得到的图像有两种解释。在上面的图片中,你可以看到阿尔伯特爱因斯坦,一旦你离开屏幕或缩小…...
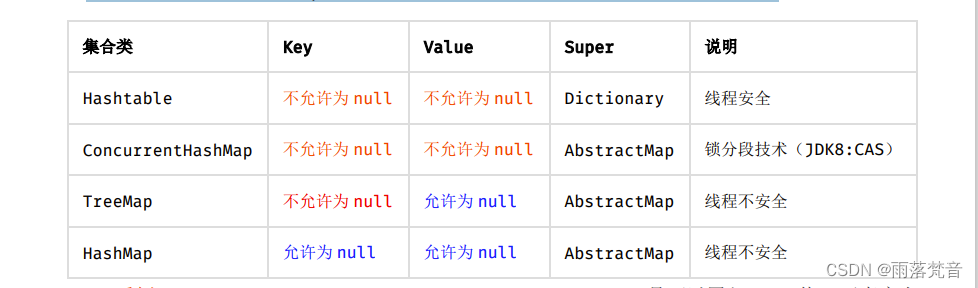
开发手册——一、编程规约_5.集合处理
这篇文章主要梳理了在java的实际开发过程中的编程规范问题。本篇文章主要借鉴于《阿里巴巴java开发手册终极版》 下面我们一起来看一下吧。 1. 【强制】关于 hashCode 和 equals 的处理,遵循如下规则: 只要重写 equals,就必须重写 hashCod…...

【elastic】elastic高可用集群部署
文章目录前言一、资源分享1、包含源码包、配置文件二、部署过程三、报错锦集四、es的部分相关命令前言 本博客内容仅为记录博主思路,仅供参考,一切以自己实践结果为准。 一、资源分享 1、包含源码包、配置文件 链接:https://pan.baidu.com…...

使用docker在3台服务器上搭建基于redis 6.x的一主两从三台均是哨兵模式
一、环境及版本说明 如果服务器已经安装了docker,则忽略此步骤,如果没有安装,则可以按照一下方式安装: 1. 在线安装(有互联网环境): 请看我这篇文章 传送阵>> 点我查看 2. 离线安装(内网环境):请看我这篇文章 传送阵>> 点我查看 说明:假设每台服务器已…...

家政维修平台实战20:权限设计
目录 1 获取工人信息2 搭建工人入口3 权限判断总结 目前我们已经搭建好了基础的用户体系,主要是分成几个表,用户表我们是记录用户的基础信息,包括手机、昵称、头像。而工人和员工各有各的表。那么就有一个问题,不同的角色…...

Java-41 深入浅出 Spring - 声明式事务的支持 事务配置 XML模式 XML+注解模式
点一下关注吧!!!非常感谢!!持续更新!!! 🚀 AI篇持续更新中!(长期更新) 目前2025年06月05日更新到: AI炼丹日志-28 - Aud…...

(转)什么是DockerCompose?它有什么作用?
一、什么是DockerCompose? DockerCompose可以基于Compose文件帮我们快速的部署分布式应用,而无需手动一个个创建和运行容器。 Compose文件是一个文本文件,通过指令定义集群中的每个容器如何运行。 DockerCompose就是把DockerFile转换成指令去运行。 …...

用docker来安装部署freeswitch记录
今天刚才测试一个callcenter的项目,所以尝试安装freeswitch 1、使用轩辕镜像 - 中国开发者首选的专业 Docker 镜像加速服务平台 编辑下面/etc/docker/daemon.json文件为 {"registry-mirrors": ["https://docker.xuanyuan.me"] }同时可以进入轩…...

实现弹窗随键盘上移居中
实现弹窗随键盘上移的核心思路 在Android中,可以通过监听键盘的显示和隐藏事件,动态调整弹窗的位置。关键点在于获取键盘高度,并计算剩余屏幕空间以重新定位弹窗。 // 在Activity或Fragment中设置键盘监听 val rootView findViewById<V…...

C++八股 —— 单例模式
文章目录 1. 基本概念2. 设计要点3. 实现方式4. 详解懒汉模式 1. 基本概念 线程安全(Thread Safety) 线程安全是指在多线程环境下,某个函数、类或代码片段能够被多个线程同时调用时,仍能保证数据的一致性和逻辑的正确性…...

回溯算法学习
一、电话号码的字母组合 import java.util.ArrayList; import java.util.List;import javax.management.loading.PrivateClassLoader;public class letterCombinations {private static final String[] KEYPAD {"", //0"", //1"abc", //2"…...

Java求职者面试指南:计算机基础与源码原理深度解析
Java求职者面试指南:计算机基础与源码原理深度解析 第一轮提问:基础概念问题 1. 请解释什么是进程和线程的区别? 面试官:进程是程序的一次执行过程,是系统进行资源分配和调度的基本单位;而线程是进程中的…...

2025年渗透测试面试题总结-腾讯[实习]科恩实验室-安全工程师(题目+回答)
安全领域各种资源,学习文档,以及工具分享、前沿信息分享、POC、EXP分享。不定期分享各种好玩的项目及好用的工具,欢迎关注。 目录 腾讯[实习]科恩实验室-安全工程师 一、网络与协议 1. TCP三次握手 2. SYN扫描原理 3. HTTPS证书机制 二…...
