当前位置： 首页 > news >正文

乐观锁与悲观锁：高并发场景下的选择

news 2026/2/9 15:38:44

在这里插入图片描述

😄 19年之后由于某些原因断更了三年，23年重新扬帆起航，推出更多优质博文，希望大家多多支持～
🌷 古之立大事者，不惟有超世之才，亦必有坚忍不拔之志
🎐 个人CSND主页——Micro麦可乐的博客
🐥《Docker实操教程》专栏以最新的Centos版本为基础进行Docker实操教程，入门到实战
🌺《RabbitMQ》本专栏主要介绍使用JAVA开发RabbitMQ的系列教程，从基础知识到项目实战
🌸《设计模式》专栏以实际的生活场景为案例进行讲解，让大家对设计模式有一个更清晰的理解
如果文章能够给大家带来一定的帮助！欢迎关注、评论互动～

乐观锁与悲观锁：高并发场景下的选择

  • 前言
  • 乐观锁
  • 悲观锁
  • 选择锁的依据
  • 结语

前言

在面对高并发的场景下，选择合适的锁策略对于保障数据一致性和提高系统性能至关重要。本文将深入探讨乐观锁和悲观锁两种常见的锁机制，分析它们在高并发环境中的优劣势，以便更好地选择适用于不同场景的锁策略。

乐观锁

原理

乐观锁假设冲突的概率较低，因此在大部分情况下不加锁，而是在更新操作时检查在此期间是否有其他事务对数据进行了修改。最常见的实现方式是使用版本号机制，每次更新都伴随着版本号的增加

优势

  • 无阻塞： 乐观锁不会阻塞其他事务的读写操作，因此在读多写少的场景下性能较好。
  • 无死锁： 由于不加锁，不存在死锁的风险。

劣势

  • 冲突处理： 当多个事务冲突时，需要有一套机制来处理这种冲突，通常是通过重试或回滚事务。

悲观锁

原理

悲观锁认为冲突的概率较高，因此在对数据进行操作前先加锁，以防止其他事务的干扰。典型的实现包括数据库的行级锁和排他锁。

优势

  • 冲突处理简单： 由于加锁操作，不需要额外的冲突处理机制。
  • 适用于写多读少： 在写多读少的场景下，悲观锁的性能较为可观。

劣势

  • 阻塞： 加锁会导致其他事务在获取锁之前阻塞，影响并发性能。
  • 死锁风险： 使用悲观锁时，存在死锁的风险，需要合理设计事务流程来避免。

选择锁的依据

1、并发度

高并发读写场景： 乐观锁更适合高并发读写场景，因为不加锁的特性使得读操作不受阻塞。
写多读少场景： 悲观锁在写多读少的场景下更具优势，因为写操作需要确保数据的一致性。

2、数据冲突概率

低冲突概率： 如果数据冲突的概率较低，可以考虑乐观锁。
高冲突概率： 如果数据冲突概率较高，悲观锁更为合适。

3、复杂度

处理复杂度： 乐观锁在处理冲突时相对较为复杂，需要一定的重试和回滚机制。
简单性： 悲观锁在处理冲突时较为简单，加锁即可。

结语

在实际应用中，乐观锁和悲观锁都有其适用的场景，选择应根据具体业务需求和并发访问的特点。在读多写少的情况下，乐观锁可以更好地发挥其性能优势；而在写多读少的情况下，悲观锁则更为适用。合理选择锁策略是高并发系统设计的关键一环，需要充分考虑业务场景和系统特性

相关文章：

乐观锁与悲观锁：高并发场景下的选择

😄 19年之后由于某些原因断更了三年，23年重新扬帆起航，推出更多优质博文，希望大家多多支持～ 🌷 古之立大事者，不惟有超世之才，亦必有坚忍不拔之志 🎐 个人CSND主页——Mi…...

编程日记 2024/1/19 12:23:47

vue2 省市区联动组件封装

在element ui中有级联选择器el-cascader，其实已经够用了，但是在实际需求中，发现el-cascader如果有三级，数据数组必须得三个才能完全展示，所以不符合实际需求,还是自定义封装吧 需求：省市区联动数组，有多少个显示多少个 这里使用element ui得el-select组件，思路是使用…...

编程日记 2024/1/19 12:21:45

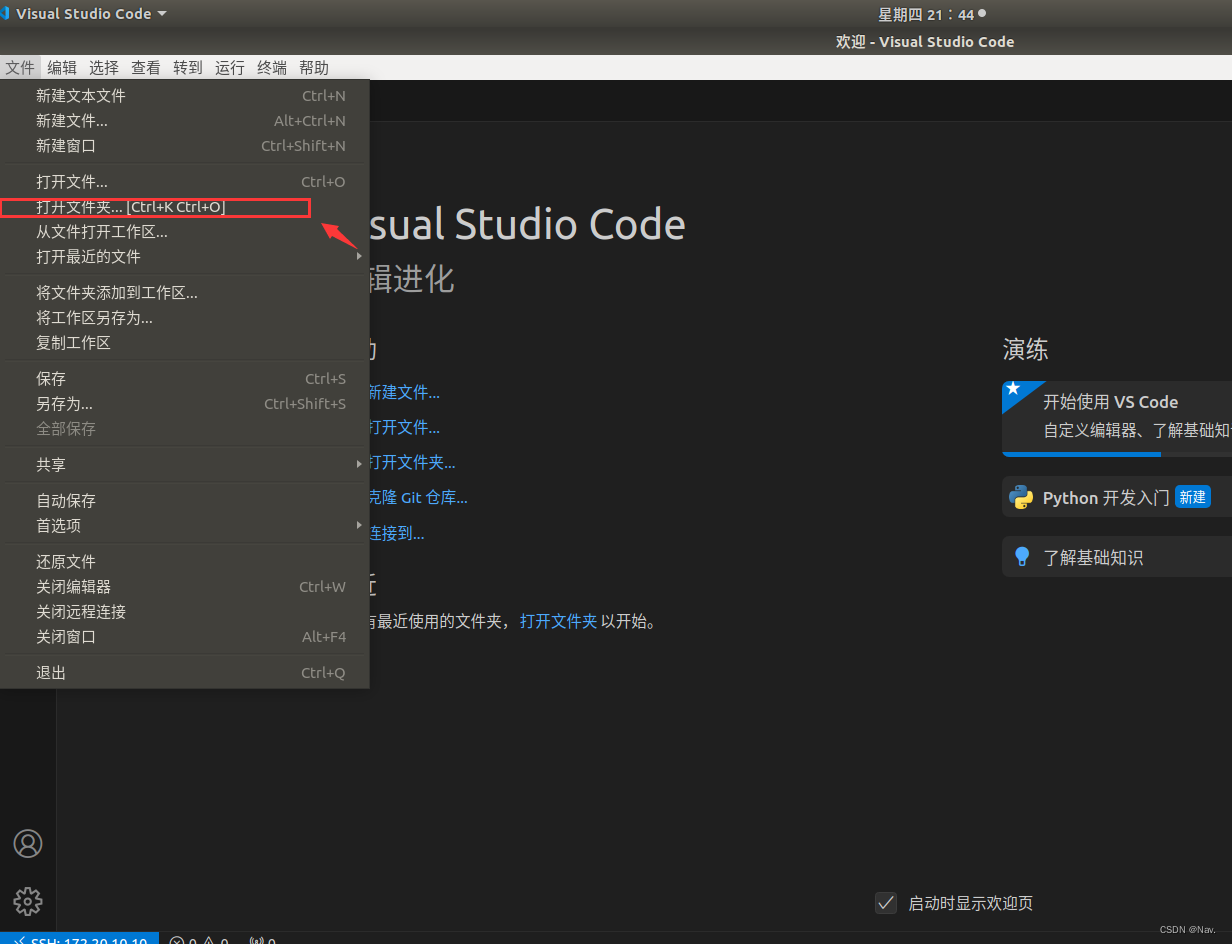
VScode远程开发

VScode远程开发 在SSH远程连接一文中，我么介绍了如何使用ssh远程连接Jetson nano端，但是也存在诸多不便，比如:编辑文件内容时，需要使用vi编辑器，且在一个终端内，无法同时编辑多个文件。本节将介绍一较为实用…...

编程日记 2024/1/19 12:20:44

芯片设计重要工具—— IBM LSF 分布式高性能计算调度平台

IBM Spectrum LSF Suites 是面向分布式高性能计算 (HPC) 的工作负载管理平台和作业调度程序。基于 Terraform 的自动化现已可用，该功能可在 IBM Cloud 上为基于 IBM Spectrum LSF 的集群供应和配置资源。 借助我们针对任务关键型 HPC 环境的集成解决方案&#xff0…...

编程日记 2024/1/19 12:19:43

RDMA Scatter Gather List详解

1. 前言 在使用RDMA操作之前，我们需要了解一些RDMA API中的一些需要的值。其中在ibv_send_wr我们需要一个sg_list的数组，sg_list是用来存放ibv_sge元素，那么什么是SGL以及什么是sge呢？对于一个使用RDMA进行开发的程序员来说&#…...

编程日记 2024/1/19 12:17:40

【动态规划】24子数组系列_最长湍流子数组_C++

题目链接：最长湍流子数组 目录 题目解析： 算法原理 1.状态表示 2.状态转移方程 3.初始化 4.填表顺序 5.返回值 编写代码 题目解析： 题目让我们求返回 arr 的 最大湍流子数组的长度 由题可得： 如果比较符号在子数组中的…...

编程日记 2024/1/19 12:15:39

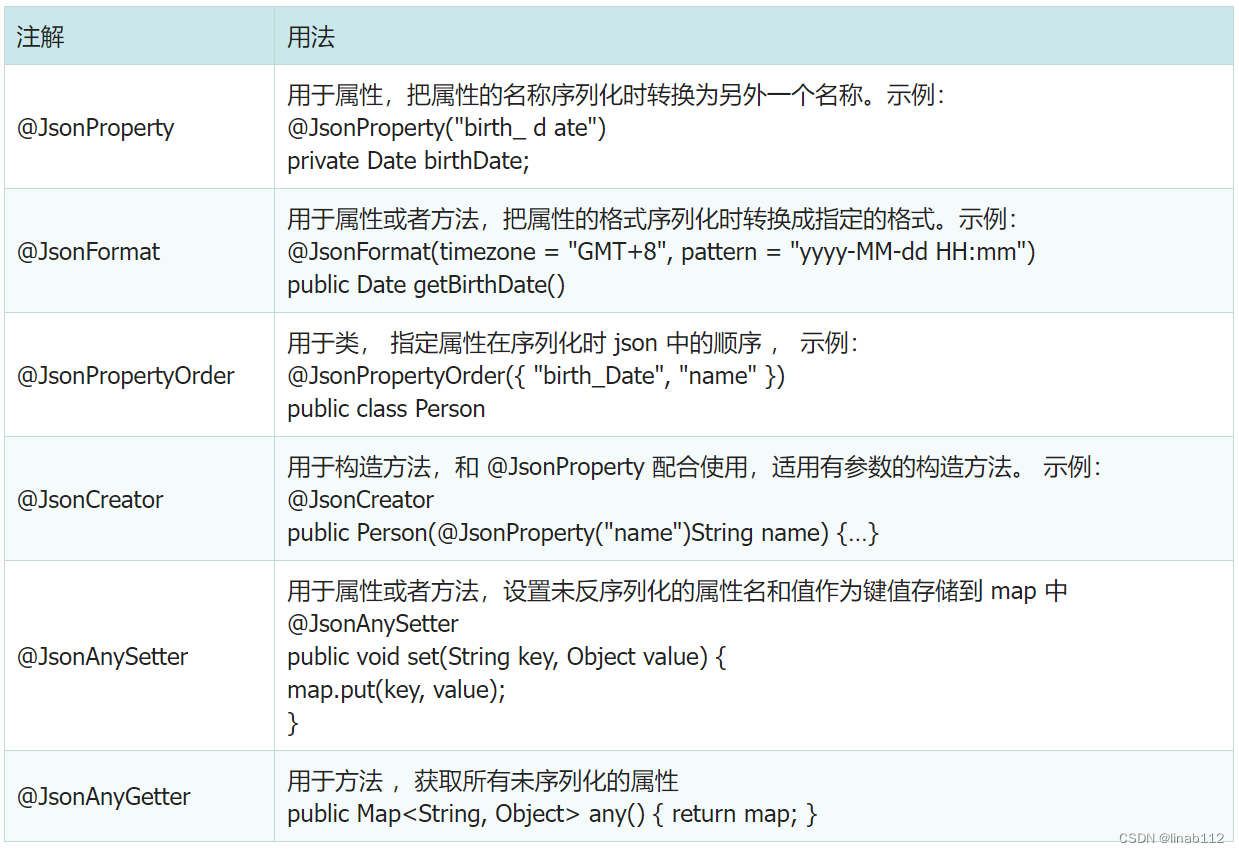
fastJson和jackson的日期数据处理

目录 1.jackson 2.fastjson 3.总结 1.jackson jackson是spring mvc默认的JSON解析方法，前端的数据序列化处理之后，后端经过反序列化处理可以直接使用实体对象进行接收。后端接口返回实体对象，经过序列化处理后前端可以接收并进行处理。 …...

编程日记 2024/1/19 12:14:37

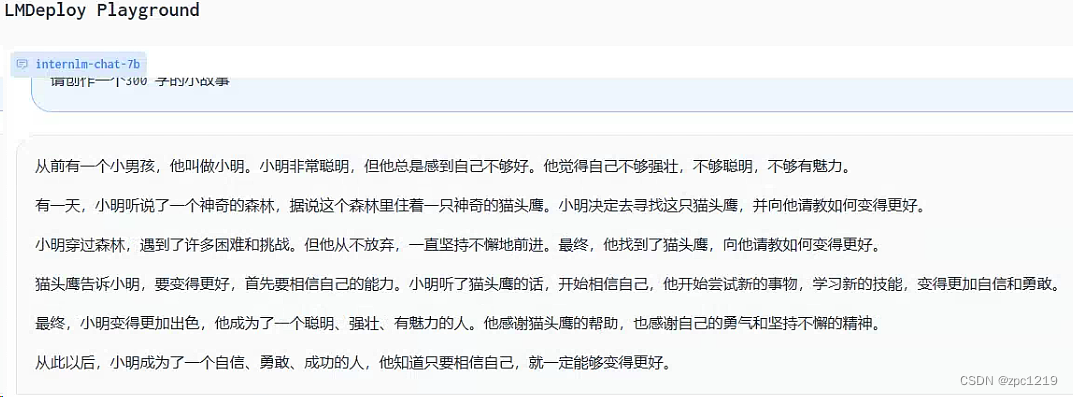
书生·浦语大模型实战营第五节课笔记及作业

LMDeploy 大模型量化部署实践 1 大模型部署背景 1.1 模型部署及大模型特点 1.2 大模型部署挑战及方案 2 LMDeploy简介 2.1 核心功能-量化 2.2 核心功能-推理引擎TurboMind 2.1 核心功能-推理服务api server 3 动手实践及作业 按照文档LMDeploy 的量化和部署中的步骤在Intern…...

编程日记 2024/1/19 12:13:36

如何在CentOS 7 中基于OpenSSL 3.0 搭建Python 3.0 环境

1、OpenSSL 1.1 原因 [rootlocalhost ~]# openssl version OpenSSL 1.0.2k-fips 26 Jan 2017 [rootlocalhost ~]#通过执行openssl version可知Linux系统已经安装了OpenSSL，但该版本较低；Python 3 要求 OpenSSL版本不能低于1.1.1，否则安装P…...

编程日记 2024/1/19 12:12:35

爬虫接口获取外汇数据(汇率，外汇储备，贸易顺差，美国CPI，M2，国债利率)

akshare是一个很好用的财经数据api接口，完全免费！！和Tushare不一样。 除了我标题显示的数据外，他还提供各种股票数据，债券数据，外汇，期货，宏观经济，基金，银行…...

编程日记 2024/1/19 12:11:34

Spring Cloud和微服务架构的关系

大话Spring Cloud 在Java悠久的历史长河中(其实也就十来年)，有一个框架自诞生之初就成了Java企业级开发领域的弄潮儿，它以开放的姿态不断引领着技术改革(我们管他叫Java领域的“改革开放”)，它就是久经考验的企业级开发框架，改革…...

编程日记 2024/1/19 12:10:33

C++：通过ofstream写入二进制文件内容

C++：通过ifstream读取二进制文件内容_c++ ifstream 二进制读取-CSDN博客 介绍了读取二进制文件的方法。 本文介绍一下写入二进制数据到文件的方法： 1.通过write #include <fstream> #include <string> using namespace std; int main() {int data = 0x0102030…...

编程日记 2024/1/19 12:09:33

系统配置dns主从服务器

一、准备两台主机&#xff0c;区分主从 二、完全区域传送 1、主DNS服务器配置 #安装相关的包 [rootoula1 ~]# yum install bind -y#关闭防火墙 [rootoula1 ~]# systemctl stop firewalld [rootoula1 ~]# setenforce 0#修改配置主文件 [rootoula1 ~]# vim /etc/named.conf opt…...

编程日记 2024/1/19 12:07:31

【git】解决网络连接问题

ssh: connect to host github.com port 22: Connection timed out $ ssh: connect to host github.com port 22: Connection timed out fatal: Could not read from remote repository. bash: ssh:: command not found bash: fatal:: command not found无效 检查网络&#xf…...

编程日记 2024/1/19 12:04:28

限制API接口访问速率

文章目录 依赖注解aophelperTest 免责声明&#xff1a;本人无意侵权&#xff0c;奈何找不到原文作者&#xff0c;也找不到网址&#xff0c;于是自己记录一下&#xff0c;如果有侵权之嫌&#xff0c;请联系我删除文章 依赖 <!-- https://mvnrepository.com/artifact/com.goo…...

编程日记 2024/1/19 12:02:27

广东省第三届职业技能大赛“网络安全项目”B模块--数字取证解析

广东省第三届职业技能大赛“网络安全项目”B模块任务书 PS: 关注鱼影安全第一部分 网络安全事件响应第二部分 数字取证调查任务 3： 网络数据包分析取证解析：第三部分 应用程序安全：需要环境可以私信博主~PS: 关注鱼影安全 模块 B 竞赛项目试题 本文件为：广东省第三届职业技…...

编程日记 2024/1/19 12:00:25

全链路压力测试：现代软件工程中的重要性

全链路压力测试不仅可以确保系统在高负载下的性能和稳定性&#xff0c;还能帮助企业进行有效的风险管理和性能优化。在快速发展的互联网时代&#xff0c;全链路压力测试已成为确保软件产品质量的关键步骤。 1、测试环境搭建 测试应在与生产环境尽可能相似的环境中进行&#xff…...

编程日记 2024/1/19 11:59:24

【计算机网络】难点、易遗忘点总结

文章目录 1. 单工通信、半双工通信和全双工通信2. TCP的三次握手和四次挥手 1. 单工通信、半双工通信和全双工通信 主要区别在于信息传输的方向和时间安排。单工通信是指信息只能在一个方向上传输的通信方式。半双工通信允许信息在两个方向上传输&#xff0c;但在任何给定的时…...

编程日记 2024/1/19 11:58:23

谷达冠楠科技：抖音开网店新手小白可以卖的产品

随着互联网的发展&#xff0c;越来越多的人选择在网上开设自己的店铺。而抖音作为目前最火的短视频平台&#xff0c;也提供了开店的功能。那么&#xff0c;对于新手小白来说&#xff0c;抖音开网店可以卖哪些产品呢? 我们可以考虑的是服装类商品。抖音上有很多时尚博主&#x…...

编程日记 2024/1/19 11:57:23

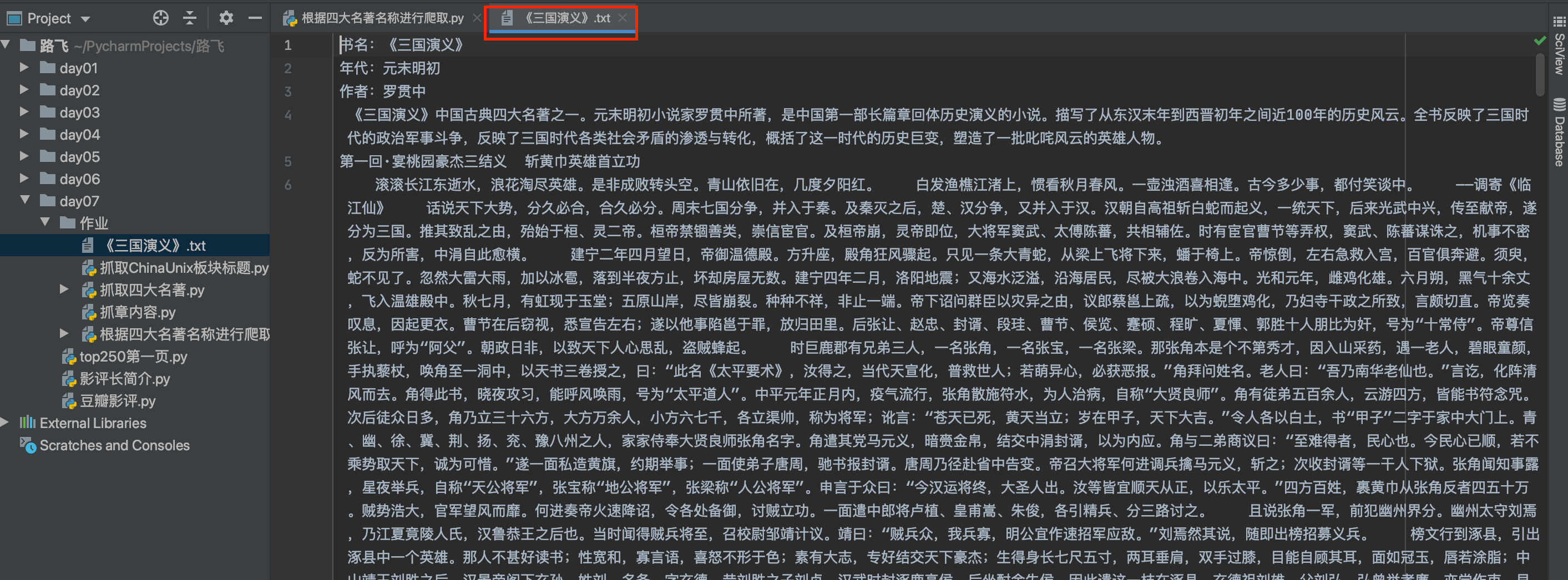
爬虫案例—根据四大名著书名抓取并存储为文本文件

爬虫案例—根据四大名著书名抓取并存储为文本文件 诗词名句网&#xff1a;https://www.shicimingju.com 目标&#xff1a;输入四大名著的书名&#xff0c;抓取名著的全部内容&#xff0c;包括书名&#xff0c;作者&#xff0c;年代及各章节内容 诗词名句网主页如下图&#x…...

编程日记 2024/1/19 11:54:20

idea大量爆红问题解决

问题描述 在学习和工作中&#xff0c;idea是程序员不可缺少的一个工具&#xff0c;但是突然在有些时候就会出现大量爆红的问题&#xff0c;发现无法跳转&#xff0c;无论是关机重启或者是替换root都无法解决 就是如上所展示的问题&#xff0c;但是程序依然可以启动。 问题解决…...

编程新知 2026/2/8 6:37:38

Java 语言特性(面试系列2)

一、SQL 基础 1. 复杂查询 &#xff08;1&#xff09;连接查询&#xff08;JOIN&#xff09; 内连接&#xff08;INNER JOIN&#xff09;&#xff1a;返回两表匹配的记录。 SELECT e.name, d.dept_name FROM employees e INNER JOIN departments d ON e.dept_id d.dept_id; 左…...

编程新知 2025/10/24 14:20:29

深入理解JavaScript设计模式之单例模式

目录 什么是单例模式为什么需要单例模式常见应用场景包括 单例模式实现透明单例模式实现不透明单例模式用代理实现单例模式javaScript中的单例模式使用命名空间使用闭包封装私有变量 惰性单例通用的惰性单例 结语 什么是单例模式 单例模式&#xff08;Singleton Pattern&#…...

编程新知 2026/1/31 17:09:43

CMake控制VS2022项目文件分组

我们可以通过 CMake 控制源文件的组织结构，使它们在 VS 解决方案资源管理器中以“组”（Filter）的形式进行分类展示。 🎯 目标 通过 CMake 脚本将 .cpp、.h 等源文件分组显示在 Visual Studio 2022 的解决方案资源管理器中。 ✅ 支持的方法汇总（共4种） 方法描述是否推荐…...

编程新知 2025/12/4 15:47:17

初探Service服务发现机制

1.Service简介 Service是将运行在一组Pod上的应用程序发布为网络服务的抽象方法。 主要功能&#xff1a;服务发现和负载均衡。 Service类型的包括ClusterIP类型、NodePort类型、LoadBalancer类型、ExternalName类型 2.Endpoints简介 Endpoints是一种Kubernetes资源&#xf…...

编程新知 2026/2/6 15:01:23

Linux 中如何提取压缩文件 ？

Linux 是一种流行的开源操作系统&#xff0c;它提供了许多工具来管理、压缩和解压缩文件。压缩文件有助于节省存储空间&#xff0c;使数据传输更快。本指南将向您展示如何在 Linux 中提取不同类型的压缩文件。 1. Unpacking ZIP Files ZIP 文件是非常常见的&#xff0c;要在 …...

编程新知 2026/2/1 5:38:25

【JavaSE】多线程基础学习笔记

多线程基础 -线程相关概念 程序&#xff08;Program&#xff09; 是为完成特定任务、用某种语言编写的一组指令的集合简单的说:就是我们写的代码 进程 进程是指运行中的程序&#xff0c;比如我们使用QQ&#xff0c;就启动了一个进程&#xff0c;操作系统就会为该进程分配内存…...

编程新知 2025/9/12 0:57:34

uniapp 字符包含的相关方法

在uniapp中&#xff0c;如果你想检查一个字符串是否包含另一个子字符串&#xff0c;你可以使用JavaScript中的includes()方法或者indexOf()方法。这两种方法都可以达到目的&#xff0c;但它们在处理方式和返回值上有所不同。 使用includes()方法 includes()方法用于判断一个字…...

编程新知 2025/9/28 19:00:18

关于uniapp展示PDF的解决方案

在 UniApp 的 H5 环境中使用 pdf-vue3 组件可以实现完整的 PDF 预览功能。以下是详细实现步骤和注意事项&#xff1a; 一、安装依赖 安装 pdf-vue3 和 PDF.js 核心库&#xff1a; npm install pdf-vue3 pdfjs-dist二、基本使用示例 <template><view class"con…...

编程新知 2025/9/18 20:16:52

Vue 模板语句的数据来源

&#x1f9e9; Vue 模板语句的数据来源&#xff1a;全方位解析 Vue 模板&#xff08;<template> 部分&#xff09;中的表达式、指令绑定&#xff08;如 v-bind, v-on&#xff09;和插值&#xff08;{{ }}&#xff09;都在一个特定的作用域内求值。这个作用域由当前 组件…...

编程新知 2026/2/1 6:18:18