【图论】树的直径
树的直径即为一棵树中距离最远的两点之间的路径
方法一:DFS
先以任意一点为起点跑一遍dfs,记录离起点距离最远的点p(这个点一定是直径的一个端点,感性理解一下不证明了),然后再以最远点再跑一遍dfs,记录此时距离最远的点q,那么pq就是该树的直接
树中有负权边时不可以用这个方法
const int N = 10000 + 10;int n, c, d[N];
vector<int> g[N];void dfs(int u, int fa)
{for (int v : E[u]){if (v == fa) continue;d[v] = d[u] + 1; // 如边有权值,把1换成权值即可if (d[v] > d[c]) c = v; // 更新最大距离的点dfs(v, u);}
}int main()
{cin >> n;for (int i = 1; i < n; i++){int u, v;scanf("%d %d", &u, &v);g[u].push_back(v), g[v].push_back(u);}dfs(1, 0); // 第一遍dfsint p = c; // 一个端点d[c] = 0;dfs(c, 0); // 第二遍dfsint q = c; // 另一个端点cout << d[c];return 0;
}
方法二:树形dp
dp[u]为以u为根的子树中离u最远的点的路径长度
转移方程(v为u的子结点):dp[u] = max(dp[u], dp[v] + w(u, v))
两条经过根结点的最长路径即为该子树中的直径
转移方程:zj = max(zj, dp[u] + dp[v] + w(u, v))
const int N = 10000 + 10;int n, zj = 0;
int dp[N];
vector<int> g[N];void dfs(int u, int fa)
{for (int v : E[u]){if (v == fa) continue;dfs(v, u);zj = max(zj, dp[u] + dp[v] + 1); // 如为有权边,把1换成权值即可dp[u] = max(dp[u], dp[v] + 1); // 如为有权边,把1换成权值即可}
}int main()
{cin >> n;for (int i = 1; i < n; i++){int u, v;cin >> u >> v;g[u].push_back(v), g[v].push_back(u);}dfs(1, 0);cout << zj << '\n';return 0;
}
相关文章:

【图论】树的直径
树的直径即为一棵树中距离最远的两点之间的路径 方法一:DFS 先以任意一点为起点跑一遍dfs,记录离起点距离最远的点p(这个点一定是直径的一个端点,感性理解一下不证明了),然后再以最远点再跑一遍dfs&#…...

制作一个Python聊天机器人
我们学习一下如何使用 ChatterBot 库在 Python 中创建聊天机器人,该库实现了各种机器学习算法来生成响应对话,还是挺不错的 什么是聊天机器人 聊天机器人也称为聊天机器人、机器人、人工代理等,基本上是由人工智能驱动的软件程序࿰…...
docker 使用 vcs/2018 Verdi等 eda 软件
好不容易在ubuntu 安装好了eda软件,转眼就发现了自己的无知。 有博主几年前就搞定了docker上的EDA工具。而且更全,更简单。只恨自己太无知啊。 Synopsys EDA Tools docker image - EDA资源使用讨论 - EETOP 创芯网论坛 (原名:电子顶级开发网…...

Git教程学习:01 Git简介与安装
目录 1 版本控制1.1 什么是版本控制系统?1.2 本地版本控制系统1.3 集中式版本控制系统1.4 分布式版本控制系统 2 Git简史3 Git的安装3.1 在Linux上安装3.2 初次运行Git前的配置 1 版本控制 1.1 什么是版本控制系统? 版本控制系统(Version Control Syst…...
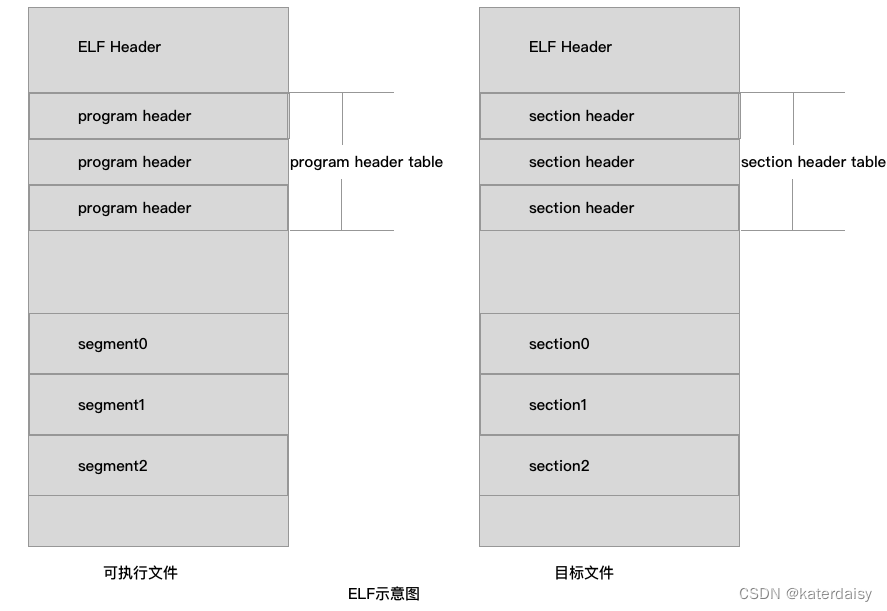
写操作系统之开发加载器
这篇文章写的很好是理解操作系统加载部分的基础 https://www.cnblogs.com/chuganghong/p/15415208.html loader的功能是: 从软盘中把操作系统内核读取到内存中。 进入保护模式。 把内存中的操作系统内核重新放置到内存中。 执行操作系统内核。 如果理解不了上面的…...

openlayers [九] 地图覆盖物overlay三种常用用法 popup弹窗,marker标注,text文本
文章目录 简介overlay 实现popup弹窗overlay 实现label 标注信息overlay实现 text 文本信息完整代码 简介 常见的地图覆盖物为这三种类型,如:popup弹窗、label标注信息、text文本信息等。 overlay 实现popup弹窗 方法详解 实例一个 new Overlay()&…...
rabbitmq-java基础详解
一、rabbitmq是什么? 1、MQ定义 MQ(Message Queue)消息队列 主要解决:异步处理、应用解耦、流量削峰等问题,是分布式系统的重要组件,从而实现高性能,高可用,可伸缩和最终一致性的架…...

openssl3.2 - 官方demo学习 - smime - smsign.c
文章目录 openssl3.2 - 官方demo学习 - smime - smsign.c概述笔记END openssl3.2 - 官方demo学习 - smime - smsign.c 概述 从证书中得到X509*和私钥指针 用证书和私钥对铭文进行签名, 得到签名后的pkcs7指针 将pkcs7指向的bio_in, 写为MIME格式的签名密文 BIO_reset() 可以…...

Klocwork—符合功能安全要求的自动化静态测试工具
产品概述 Klocwork是Perforce公司产品,主要用于C、C、C#、Java、 python和Kotlin代码的自动化静态分析工作,可以提供编码规则检查、代码质量度量、测试结果管理等功能。Klocwork可以扩展到大多数规模的项目,与大型复杂环境、各种开发工具集成…...
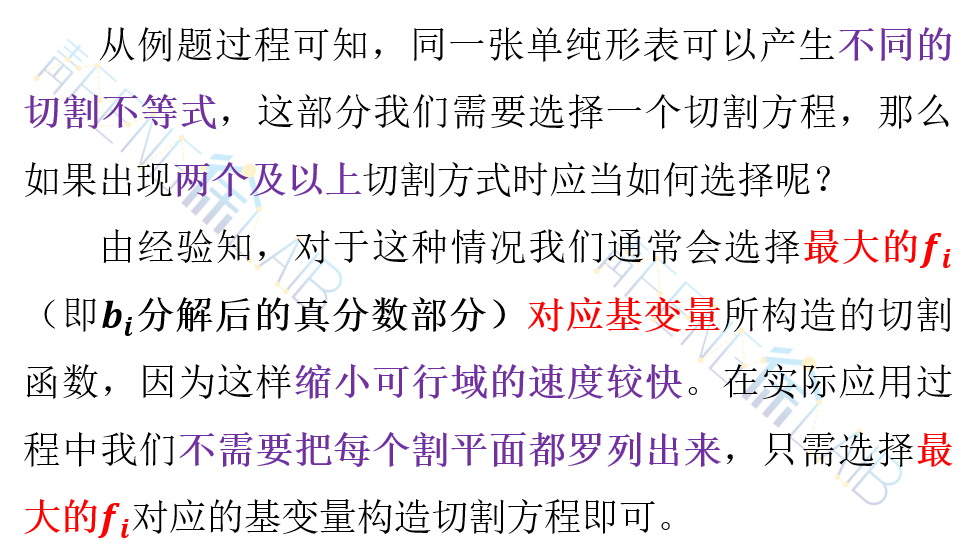
运筹说 第56期 | 整数规划的数学模型割平面法
前几章讨论过的线性规划问题的一个共同特点是:最优解的取值可以是分数或者小数。然而,在许多实际问题中,决策者要求最优解必须是整数,例如公交车的车辆数、员工的人数、机器的台数、产品的件数等。那么,我们能否将得到…...

vue中内置指令v-model的作用和常见使用方法介绍以及在自定义组件上支持
文章目录 一、v-model是什么二、什么是语法糖三、v-model常见的用法1、对于输入框(input):2、对于复选框(checkbox):3、对于选择框(select):4、对于组件(comp…...

大模型推理引擎面试复习大纲
Transformer原理 基本组成、注意力机制含义 transformer有哪些模块,各个模块有什么作用? transformer的模块可以分为以下几类: Encoder模块:transformer的编码器,它由多个相同的encoder层堆叠而成,每个enc…...

网络安全 | 苹果承认 GPU 安全漏洞存在,iPhone 12、M2 MacBook Air 等受影响
1 月 17 日消息,苹果公司确认了近期出现的有关 Apple GPU 存在安全漏洞的报告,并承认 iPhone 12 和 M2 MacBook Air 受影响。 该漏洞可能使攻击者窃取由芯片处理的数据,包括与 ChatGPT 的对话内容等隐私信息。 安全研究人员发现,…...

C++ 数论相关题目(约数)
1、试除法求约数 主要还是可以成对的求约数进行优化,不然会超时。 时间复杂度根号n #include <iostream> #include <vector> #include <algorithm>using namespace std;int n;vector<int> solve(int a) {vector<int> res;for(int i…...

freeswitch on centos dockerfile模式
概述 freeswitch是一款简单好用的VOIP开源软交换平台。 centos7 docker上编译安装fs的流程记录,本文使用dockerfile模式。 环境 docker engine:Version 24.0.6 centos docker:7 freeswitch:v1.6.20 dockerfile 创建空目录…...

Hologres + Flink 流式湖仓建设
Hologres + Flink 流式湖仓建设 1 Flink + Hologres 特性1.2 实时维表 Lookup1.3 高性能实时写入与更新1.4 多流合并1.5 Hologres 作为 Flink 的数据源1.6 元数据自动发现与更新2 传统实时数仓分层方案2.1传统实时数仓分层方案 1:流式 ETL2.2 传统实时数仓分层方案 2:定时调度…...
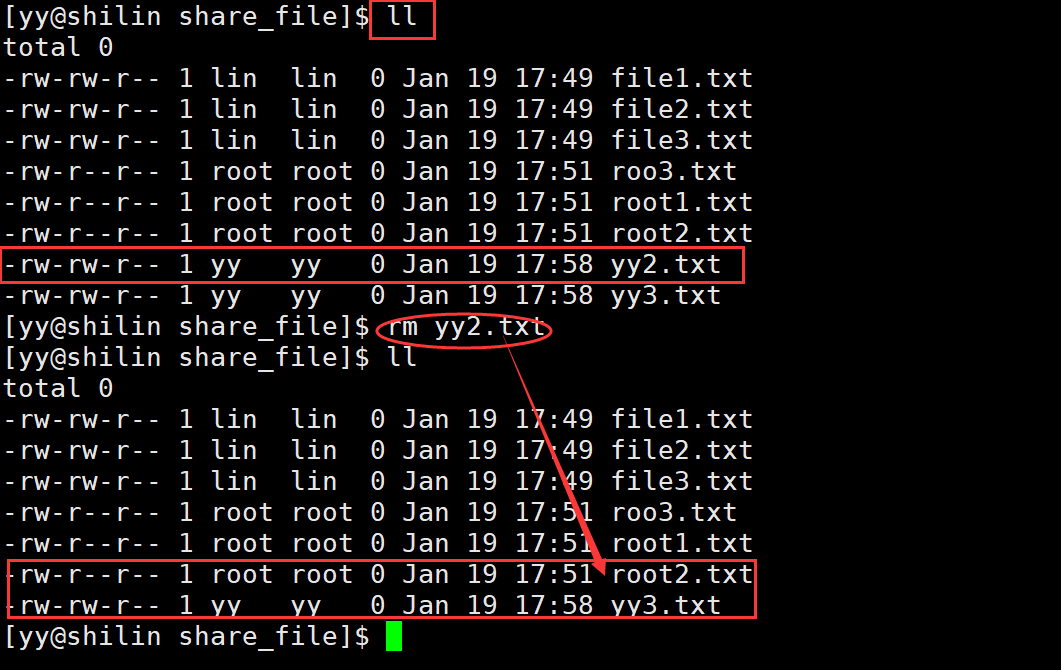
Linux粘滞位的理解,什么是粘滞位?
文章目录 前言如何理解?粘滞位的操作最后总结一下 前言 粘滞位(Stickybit),或粘着位,是Unix文件系统权限的一个旗标。最常见的用法在目录上设置粘滞位,如此以来,只有目录内文件的所有者或者root…...

Stable Diffusion的结构要被淘汰了吗?详细解读谷歌最新大杀器VideoPoet
Diffusion Models视频生成-博客汇总 前言:视频生成领域长期被Stable Diffusion统治,大部分的方式都是在预训练的图片Stable Diffusion的基础上加入时间层,学习动态信息。虽然有CoDi《【NeurIPS 2023】多模态联合视频生成大模型CoDi》等模型尝试过突破这一结构的局限,但是都…...

深度学习与大数据推动下的自然语言处理革命
引言: 在当今数字化时代,深度学习和大数据技术的迅猛发展为自然语言处理(Natural Language Processing, NLP)领域注入了新的活力。这些技术的进步不仅推动了计算机对人类语言理解与生成的能力,也在搜索引擎、语音助手、…...

产品经理必备之最强管理项目过程工具----禅道
目录 一.禅道的下载安装 二.禅道的使用 2.1 创建用户 2.2 产品经理的角色 2.3 项目经理的角色 研发的角色 2.4 测试主管的角色 研发角色 三.禅道使用的泳道图 一.禅道的下载安装 官网:项目管理软件 开源项目管理软件 免费项目管理软件 IPD管理软件 - 禅…...

生成xcframework
打包 XCFramework 的方法 XCFramework 是苹果推出的一种多平台二进制分发格式,可以包含多个架构和平台的代码。打包 XCFramework 通常用于分发库或框架。 使用 Xcode 命令行工具打包 通过 xcodebuild 命令可以打包 XCFramework。确保项目已经配置好需要支持的平台…...

调用支付宝接口响应40004 SYSTEM_ERROR问题排查
在对接支付宝API的时候,遇到了一些问题,记录一下排查过程。 Body:{"datadigital_fincloud_generalsaas_face_certify_initialize_response":{"msg":"Business Failed","code":"40004","sub_msg…...

反向工程与模型迁移:打造未来商品详情API的可持续创新体系
在电商行业蓬勃发展的当下,商品详情API作为连接电商平台与开发者、商家及用户的关键纽带,其重要性日益凸显。传统商品详情API主要聚焦于商品基本信息(如名称、价格、库存等)的获取与展示,已难以满足市场对个性化、智能…...

JavaScript 中的 ES|QL:利用 Apache Arrow 工具
作者:来自 Elastic Jeffrey Rengifo 学习如何将 ES|QL 与 JavaScript 的 Apache Arrow 客户端工具一起使用。 想获得 Elastic 认证吗?了解下一期 Elasticsearch Engineer 培训的时间吧! Elasticsearch 拥有众多新功能,助你为自己…...

DAY 47
三、通道注意力 3.1 通道注意力的定义 # 新增:通道注意力模块(SE模块) class ChannelAttention(nn.Module):"""通道注意力模块(Squeeze-and-Excitation)"""def __init__(self, in_channels, reduction_rat…...

Python实现prophet 理论及参数优化
文章目录 Prophet理论及模型参数介绍Python代码完整实现prophet 添加外部数据进行模型优化 之前初步学习prophet的时候,写过一篇简单实现,后期随着对该模型的深入研究,本次记录涉及到prophet 的公式以及参数调优,从公式可以更直观…...

P3 QT项目----记事本(3.8)
3.8 记事本项目总结 项目源码 1.main.cpp #include "widget.h" #include <QApplication> int main(int argc, char *argv[]) {QApplication a(argc, argv);Widget w;w.show();return a.exec(); } 2.widget.cpp #include "widget.h" #include &q…...

学习STC51单片机31(芯片为STC89C52RCRC)OLED显示屏1
每日一言 生活的美好,总是藏在那些你咬牙坚持的日子里。 硬件:OLED 以后要用到OLED的时候找到这个文件 OLED的设备地址 SSD1306"SSD" 是品牌缩写,"1306" 是产品编号。 驱动 OLED 屏幕的 IIC 总线数据传输格式 示意图 …...

C++中string流知识详解和示例
一、概览与类体系 C 提供三种基于内存字符串的流,定义在 <sstream> 中: std::istringstream:输入流,从已有字符串中读取并解析。std::ostringstream:输出流,向内部缓冲区写入内容,最终取…...

AI编程--插件对比分析:CodeRider、GitHub Copilot及其他
AI编程插件对比分析:CodeRider、GitHub Copilot及其他 随着人工智能技术的快速发展,AI编程插件已成为提升开发者生产力的重要工具。CodeRider和GitHub Copilot作为市场上的领先者,分别以其独特的特性和生态系统吸引了大量开发者。本文将从功…...
