基于网络爬虫的微博热点分析,包括文本分析和主题分析
基于Python的网络爬虫的微博热点分析是一项技术上具有挑战性的任务。我们使用requests库来获取微博热点数据,并使用pandas对数据进行处理和分析。为了更好地理解微博热点话题,我们采用LDA主题分析方法,结合jieba分词工具将文本分割成有意义的词语。此外,我们还使用snownlp情感分析库来评估微博热点话题的情感倾向。
在实施该分析过程中,我们首先通过网络爬虫技术从微博平台上收集热点数据。然后,使用pandas库对数据进行清洗、去重和预处理,以便更好地理解数据。接下来,我们使用jieba对微博内容进行分词处理,将其转化为有意义的词语。随后,我们运用LDA主题分析算法对微博热点话题进行建模和分类,以揭示话题之间的关联和趋势。最后,我们使用matplotlib库进行数据可视化,将分析结果以图表形式呈现,帮助用户更直观地了解微博热点话题的情况。通过这个基于Python的网络爬虫的微博热点分析流程,我们可以更深入地了解微博用户的关注点和情感倾向。这对于舆情监测、市场调研和品牌管理等领域都具有重要的应用价值。同时,该分析流程也为其他社交媒体平台的热点分析提供了参考和借鉴。
- 网络爬虫的程序架构及整体执行流程
1、网络爬虫程序框架
基于Python的网络爬虫的微博热点分析项目,以下是网络爬虫程序框架:
导入所需的库:导入requests库用于发送HTTP请求,导入BeautifulSoup库用于解析HTML页面。
构造URL:根据微博热点数据的URL结构,构造需要访问的URL。可以通过添加查询参数来获取特定话题、时间范围或其他条件的数据。
发送请求并获取响应:使用requests库发送GET请求,将URL作为参数传递给get()函数,并将响应保存在变量中。
解析HTML页面:利用BeautifulSoup库对响应进行解析,提取出需要的数据,如微博内容、用户信息和评论等。
数据处理和存储:将解析得到的数据进行清洗、去重和格式化处理,然后可以选择将数据保存到文件中或存储在数据库中,以备后续分析使用。
重复步骤2-5:根据需求,可以设置循环或递归,以便获取多个页面的数据或持续监测微博热点。
实际开发中可能需要考虑更多的细节和边界情况,比如处理反爬措施、设置请求头部信息、处理异常情况等。通过这个框架,可以构建一个基本的网络爬虫程序,用于采集微博热点数据供后续分析使用。网络爬虫程序架构如图1所示。

图1网络爬虫程序架构图
2、网络爬虫的整体流程
- 获取初始URL;
- 发送请求并获取响应;
- 解析HTML页面;
- 数据处理和存储;
- 分析是否满足停止条件,并进入下一个循环。
网络爬虫的整体流程图如图2所示。
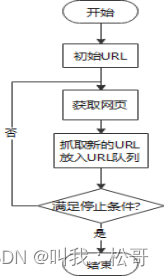
图2 网络爬虫的整体流程图
3、需求分析
数据采集需求:通过使用requests库实现微博热点数据的采集。需要获取最新和最热门的微博热点话题数据,包括话题内容、用户评论和转发数量等信息。
数据清洗和预处理需求:利用pandas库对采集到的数据进行清洗、去重和预处理,以便后续的数据分析和建模。需要处理缺失值、异常值和不一致的数据,并将其转换为适合分析的格式。
文本分析需求:使用jieba分词工具将微博内容进行分词,将文本转化为有意义的词语。这样可以更好地理解微博热点话题的关键词和主题。同时,需要应用LDA主题分析算法,从大量数据中提取潜在的话题模式和关联性。
情感分析需求:利用snownlp情感分析库对微博热点话题的情感倾向进行评估。这可以帮助我们了解用户对话题的情感态度和意见,从而更全面地分析微博热点话题的影响力和用户反馈。
可视化需求:使用matplotlib库进行数据可视化,将分析结果以图表的形式呈现出来。这样可以直观地展示微博热点话题的趋势、情感倾向和关联性,帮助用户更好地理解和解读分析结果。
4、网络爬虫系统设计
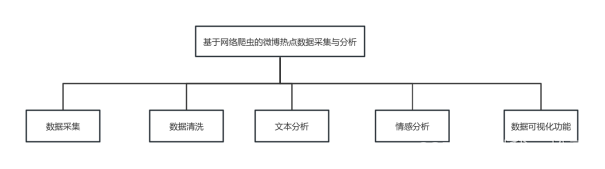
数据采集模块:使用requests库发送HTTP请求,根据微博热点数据的URL结构构造请求,并获取响应。解析HTML页面,提取所需的数据,如微博内容、用户信息和评论等。
数据清洗和预处理模块:使用pandas库对采集到的数据进行清洗、去重和预处理。处理缺失值、异常值和不一致的数据,将其转换为适合分析的格式。
文本分析模块:使用jieba分词工具将微博内容进行分词处理,将文本转化为有意义的词语。应用LDA主题分析算法,从大量数据中提取潜在的话题模式和关联性。
情感分析模块:利用snownlp情感分析库对微博热点话题的情感倾向进行评估。分析文本的情感色彩,了解用户对话题的情感态度和意见。
可视化模块:使用matplotlib库进行数据可视化,将分析结果以图表的形式呈现出来。生成趋势图、饼图等可视化工具,直观地展示微博热点话题的特征和趋势。。
根据以上设计思路和设计原则得出功能结构图。如图3所示。
5、网页数据的爬取
基于Python的网络爬虫对微博热点数据进行爬取,并将爬取到的数据存储到CSV文件中。具体实现过程如下:
首先,使用requests库发送HTTP请求,模拟用户访问微博热点页面。通过循环遍历不同页数,获取每一页上的微博博文的链接。
然后,使用BeautifulSoup库解析HTML页面,提取出博文的编号和其他相关信息。在解析过程中,还包括一些正则表达式的处理,以获取更精确的数据。
接着,利用requests库再次发送HTTP请求,获取每篇博文的详细内容。根据博文编号构造请求URL,并携带必要的参数,如Cookie和Headers等,以模拟登录状态。
在获取到博文详细内容后,使用json库解析响应结果,提取出博文的正文、发布人ID、点赞数、评论数、转发数等关键信息。
根据需要,对博文的全文进行展开处理,如果有全文内容,则提取全文内容;否则,将正文内容作为全文。
最后,将爬取到的数据以列表形式存储,并使用csv库将数据写入到CSV文件中。
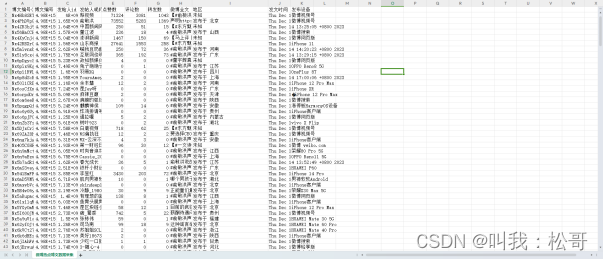
该数据爬取功能的作用是获取微博热点话题下的博文数据,包括博文的文本内容、点赞数、评论数等信息。这些数据可以用于后续的数据分析和可视化,如使用pandas库对数据进行清洗和处理,使用matplotlib库将结果可视化呈现,以便更好地理解微博热点话题的趋势、情感倾向和关联性。
通过这个数据爬取功能,可以实现对微博热点话题的全面分析和洞察,帮助用户了解公众舆论、用户需求和市场趋势,从而支持舆情监测、市场调研、品牌管理等领域的决策和判断。最后抓取数据代码运行结果如图4所示。
- SnowNLP库进行情感分析
通过使用SnowNLP库对微博热点博文的内容进行情感分析,计算每篇博文的情感分数。根据情感分数的大小,将博文划分为积极、中性或消极情感,并将情感分数和情感分析结果添加到数据中。这样可以帮助用户了解微博热点话题下博文的情感倾向和态度,从而更全面地分析和解读微博热点话题的影响力和用户反馈。代码如下所示。

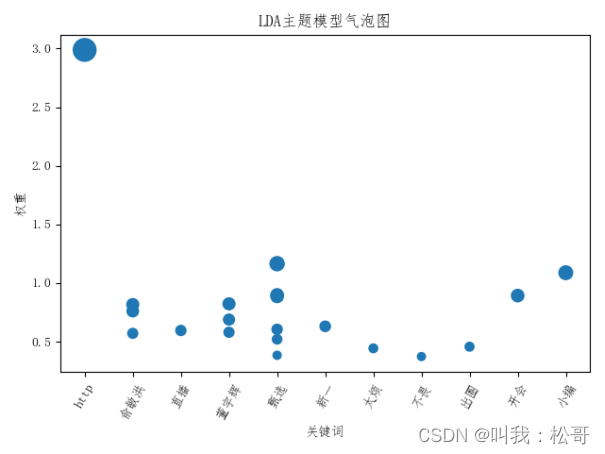
LDA主题分析
通过plt.scatter()函数,可以将两个变量的关系以散点图的形式呈现。在微博热点分析中,可以使用散点图展示关键词和权重之间的关系,例如将关键词作为横坐标,权重作为纵坐标,以点的大小或颜色表示权重的大小,从而观察关键词的分布情况和权重的差异。
相关文章:

基于网络爬虫的微博热点分析,包括文本分析和主题分析
基于Python的网络爬虫的微博热点分析是一项技术上具有挑战性的任务。我们使用requests库来获取微博热点数据,并使用pandas对数据进行处理和分析。为了更好地理解微博热点话题,我们采用LDA主题分析方法,结合jieba分词工具将文本分割成有意义的…...

前端图片转base64 方法
在uni-app、Vue.js或其他前端框架中,将图片转换为Base64编码的过程是相似的。以下是一个简单的示例,说明如何在这些环境中使用JavaScript将图片转换为Base64编码。 1. HTML部分 首先,你需要在HTML中放置一个文件输入元素,用于选…...
双向链表)
Go语言数据结构(一)双向链表
list容器 Go语言中list容器定义在"container/list"包中,实现了一个双向链表。本文第一部分总结源码包中的方法,第二部分展示使用list包的常见示例用法以及刷题时的用法。 食用指南:先看第二部分的常用示例用法然后再用到时在第一部…...

【MySql】MySQL 如何创建新用户
具体代码与实现方法 登录 MySQL: 使用 root 用户或具有相应权限的用户登录到 MySQL。可以使用以下命令: mysql -u root -p这里 -u 后面跟的是用户名,-p 表示提示输入密码。 创建新用户: 使用以下 SQL 命令创建新用户:…...

【DFS】200.岛屿数量
题目 法1:DFS 最简单的DFS必须掌握!!! class Solution {public int numIslands(char[][] grid) {int m grid.length, n grid[0].length, ans 0;if (m 0 || n 0) {return ans;}boolean[][] visited new boolean[m][n];for…...
)
Vue动态添加新的属性到实例上(vue的问题)
当我们去看vue文档的时候,发现如果在实例创建之后添加新的属性到实例上,它不会触发视图更新。比如我们我们开始创建了一个对象实例,在实例创建之后为其增加新的属性,我们发现这个属性不能生效,此时需要使用this.$set()方法。 &…...

HarmonyOS应用开发者高级认证
一、判断题 云函数打包完成后,需要到AppGallery Connect创建对应函数的触发器才可以在端侧中调用(错) 在column和Row容器组件中,aligntems用于设置子组件在主轴方向上的对齐格式,justifycontent用于设置子组件在交叉轴…...

设计模式复盘
一、背景 在项目中,对于单据的扩展是基于类似于接口扩展实现的。从业务横行来看,业务有A、B、C;从纵向来看,单个业务逻辑编排也可以划分为基础数据查询,决策判断,逻辑执行三大块。 单据扩展:平…...

电力能源三维可视化合集 | 图扑数字孪生
电力能源是现代社会发展和运行的基石,渗透于工业、商业、农业、家庭生活等方方面面,它为经济、生活质量、环境保护和社会发展提供了巨大的机会和潜力。图扑软件应用自研 HT for Web 强大的渲染引擎,助力现代化的电力能源数字孪生场景…...

What is `@Repository` does?
Repository 是Spring注解,标识数据访问层组件(DAO, Data Access Object) 当一个类被标记为 Repository 时: 1、组件扫描与自动代理: Spring通过组件扫描(Component Scan)机制发现带有 Reposit…...
c# 自定义 滑块TrackBar
辛苦半天做出来的,如果觉得好用,记得点赞 效果图如下: 具体操作: 1 、添加代码(代码在下面),重新生成下整个工程,在工具栏中就出现控件,将控件拖到窗体中 2、只需要调整…...

MyBatis整合分页插件PageHelper的使用和说明
MyBatis,作为目前流行的ORM框架,大大方便了日常开发。而对于分页查询,虽然可以通过SQL的limit语句实现,但是比较繁琐。而MyBatis PageHelper的出现,则解决了这一痛点。这里将介绍如何在Spring Boot、MyBatis的环境中通…...

情人节专属--HTML制作情人节告白爱心
💕效果展示 💕html展示 <!DOCTYPE html> <html lang="en" > <head>...

带你学C语言-指针(4)
目录 编辑 ⚾0.前言 🏀1.回调函数 ⚽2.qsort 🏉2.1 qsort函数的模拟实现 🎾3.sizeof与strlen对比 🎾4.结束语 ⚾0.前言 言C之言,聊C之识,以C会友,共向远方。各位CSDN的各位你们好啊&…...

ACL访问控制列表
ACL:访问控制列表 在路由器流量进或出接口上,匹配流量产生动作-- 允许 拒绝 (访问限制)定义感兴趣流量--- 匹配流量后,将流量提交给其他的协议进行策略 匹配规则: 至上而下逐一匹配,上条匹配按…...
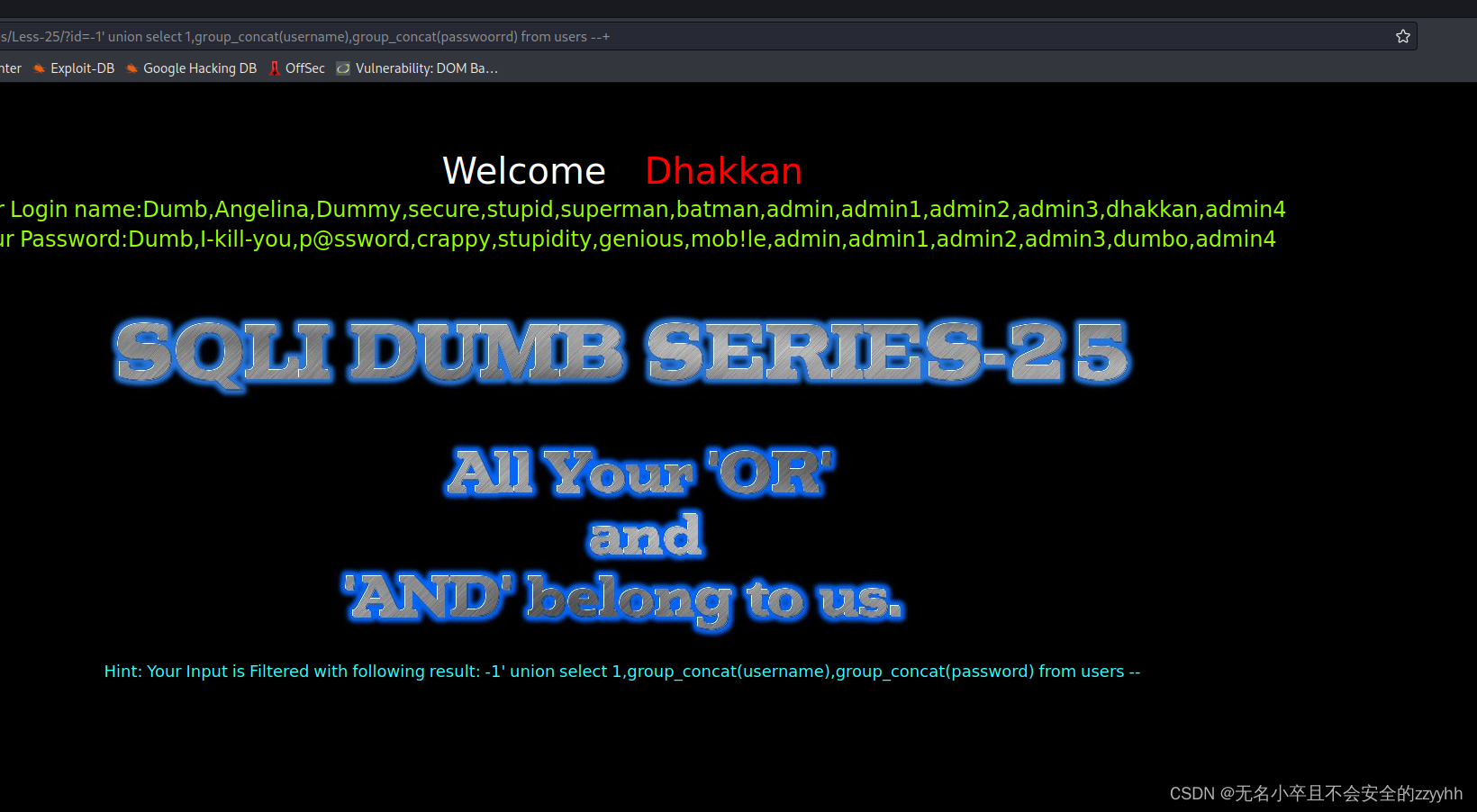
sqli-labs关卡25(基于get提交的过滤and和or的联合注入)
文章目录 前言一、回顾上一关知识点二、靶场第二十五关通关思路1、判断注入点2、爆字段个数3、爆显位位置4、爆数据库名5、爆数据库表名6、爆数据库列名7、爆数据库数据 总结 前言 此文章只用于学习和反思巩固sql注入知识,禁止用于做非法攻击。注意靶场是可以练习的…...

机器学习周刊第六期:哈佛大学机器学习课、Chatbot Ul 2.0 、LangChain v0.1.0、Mixtral 8x7B
— date: 2024/01/08 — 吴恩达和Langchain合作开发了JavaScript 生成式 AI 短期课程:《使用 LangChain.js 构建 LLM 应用程序》 大家好,欢迎收看第六期机器学习周刊 本期介绍10个内容,涉及Python、机器学习、大模型等,目录如下ÿ…...

【算法与数据结构】Java实现查找与排序
文章目录 第一部分:查找算法二分查找插值查找分块查找哈希查找树表查找 第二部分:排序算法冒泡排序选择排序插入排序快速排序 总结 第一部分:查找算法 二分查找 也叫做折半查找,属于有序查找算法。 前提条件:数组数据…...
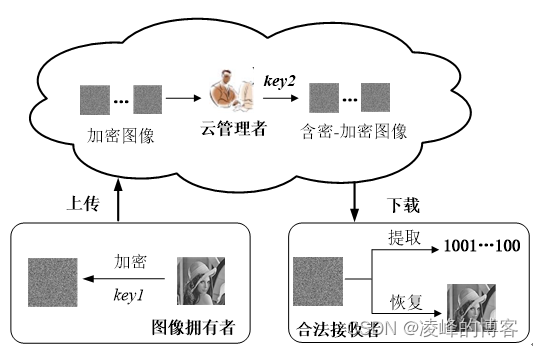
边缘计算的挑战和机遇(结合RDH-EI)
边缘计算的挑战和机遇 边缘计算面临着数据安全与隐私保护、网络稳定性等挑战,但同时也带来了更强的实时性和本地处理能力,为企业降低了成本和压力,提高了数据处理效率。因此,边缘计算既带来了挑战也带来了机遇,需要我…...

详解IP安全:IPSec协议簇 | AH协议 | ESP协议 | IKE协议_ipsec esp
目录 IP安全概述 IPSec协议簇 IPSec的实现方式 AH(Authentication Header,认证头) ESP(Encapsulating Security Payload,封装安全载荷) IKE(Internet Key Exchange,因特网密钥…...

Linux应用开发之网络套接字编程(实例篇)
服务端与客户端单连接 服务端代码 #include <sys/socket.h> #include <sys/types.h> #include <netinet/in.h> #include <stdio.h> #include <stdlib.h> #include <string.h> #include <arpa/inet.h> #include <pthread.h> …...

[10-3]软件I2C读写MPU6050 江协科技学习笔记(16个知识点)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16...

Robots.txt 文件
什么是robots.txt? robots.txt 是一个位于网站根目录下的文本文件(如:https://example.com/robots.txt),它用于指导网络爬虫(如搜索引擎的蜘蛛程序)如何抓取该网站的内容。这个文件遵循 Robots…...

PL0语法,分析器实现!
简介 PL/0 是一种简单的编程语言,通常用于教学编译原理。它的语法结构清晰,功能包括常量定义、变量声明、过程(子程序)定义以及基本的控制结构(如条件语句和循环语句)。 PL/0 语法规范 PL/0 是一种教学用的小型编程语言,由 Niklaus Wirth 设计,用于展示编译原理的核…...

AI,如何重构理解、匹配与决策?
AI 时代,我们如何理解消费? 作者|王彬 封面|Unplash 人们通过信息理解世界。 曾几何时,PC 与移动互联网重塑了人们的购物路径:信息变得唾手可得,商品决策变得高度依赖内容。 但 AI 时代的来…...

云原生玩法三问:构建自定义开发环境
云原生玩法三问:构建自定义开发环境 引言 临时运维一个古董项目,无文档,无环境,无交接人,俗称三无。 运行设备的环境老,本地环境版本高,ssh不过去。正好最近对 腾讯出品的云原生 cnb 感兴趣&…...

android13 app的触摸问题定位分析流程
一、知识点 一般来说,触摸问题都是app层面出问题,我们可以在ViewRootImpl.java添加log的方式定位;如果是touchableRegion的计算问题,就会相对比较麻烦了,需要通过adb shell dumpsys input > input.log指令,且通过打印堆栈的方式,逐步定位问题,并找到修改方案。 问题…...

Cilium动手实验室: 精通之旅---13.Cilium LoadBalancer IPAM and L2 Service Announcement
Cilium动手实验室: 精通之旅---13.Cilium LoadBalancer IPAM and L2 Service Announcement 1. LAB环境2. L2公告策略2.1 部署Death Star2.2 访问服务2.3 部署L2公告策略2.4 服务宣告 3. 可视化 ARP 流量3.1 部署新服务3.2 准备可视化3.3 再次请求 4. 自动IPAM4.1 IPAM Pool4.2 …...

学习一下用鸿蒙DevEco Studio HarmonyOS5实现百度地图
在鸿蒙(HarmonyOS5)中集成百度地图,可以通过以下步骤和技术方案实现。结合鸿蒙的分布式能力和百度地图的API,可以构建跨设备的定位、导航和地图展示功能。 1. 鸿蒙环境准备 开发工具:下载安装 De…...

如何配置一个sql server使得其它用户可以通过excel odbc获取数据
要让其他用户通过 Excel 使用 ODBC 连接到 SQL Server 获取数据,你需要完成以下配置步骤: ✅ 一、在 SQL Server 端配置(服务器设置) 1. 启用 TCP/IP 协议 打开 “SQL Server 配置管理器”。导航到:SQL Server 网络配…...
