蓝桥杯备战 每日一题 (2)

今天的题目是回忆迷宫
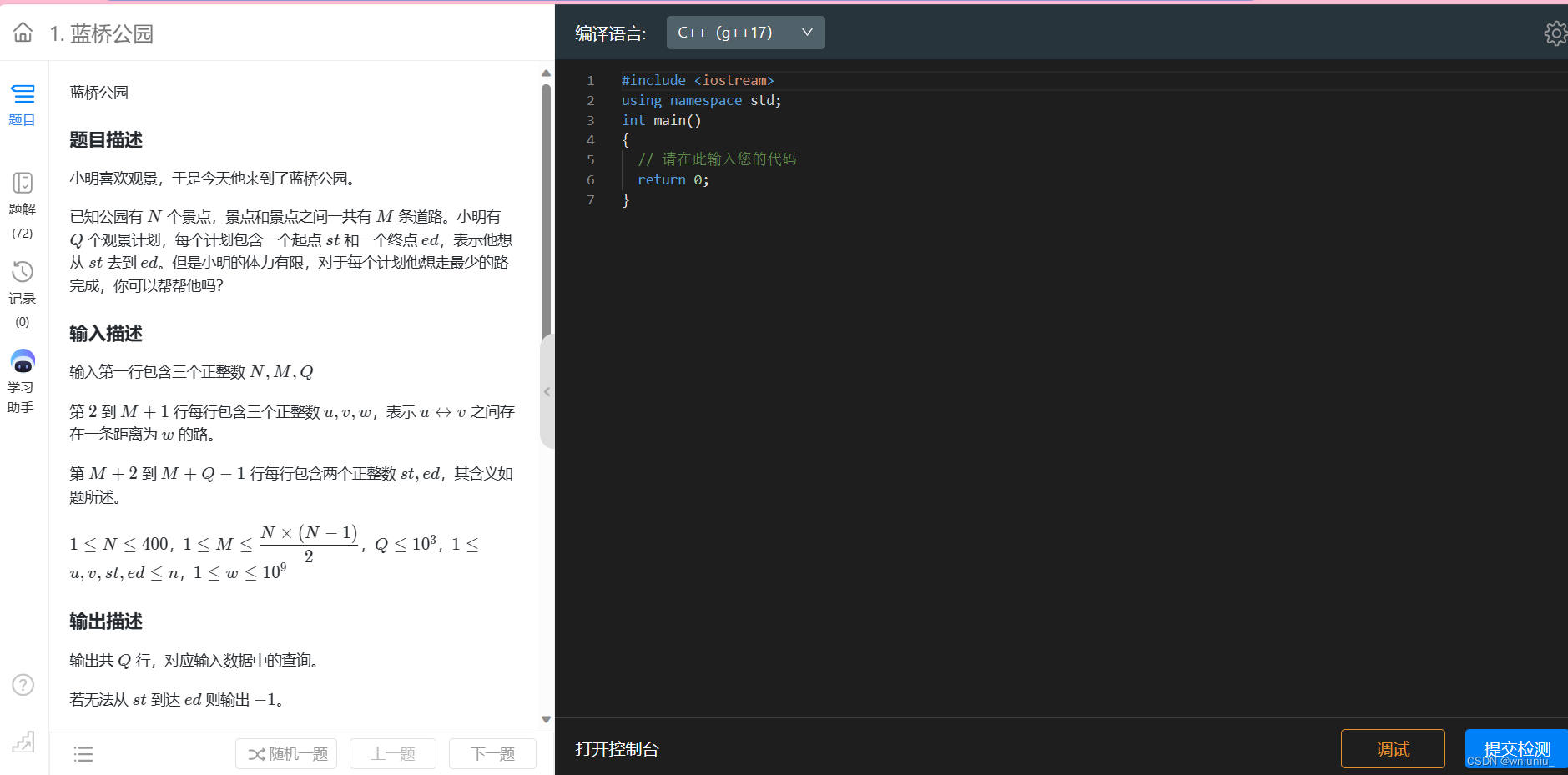
这个题目我们来熟悉一下 弗洛伊德算法 的代码模板
弗洛伊德算法用来处理最短路径问题
弗洛伊德算法(Floyd’s algorithm)用于解决图中所有节点对之间的最短路径问题。算法的基本思路是通过逐步迭代更新节点对之间的最短路径长度,直到得到所有节点对之间的最短路径。
以下是弗洛伊德算法的大致思路:
-
初始化距离矩阵:创建一个二维矩阵,称为距离矩阵,用于存储节点对之间的最短路径长度。初始时,距离矩阵的值为图中节点之间的直接距离,如果两个节点之间没有直接边相连,则距离为无穷大。
-
迭代更新最短路径:通过遍历所有节点,对于每一对节点 (i, j),检查是否存在一个中间节点 k,使得从节点 i 到节点 j 经过节点 k 的路径长度比直接从 i 到 j 的路径更短。如果存在这样的中间节点 k,则更新距离矩阵中节点 i 到节点 j 的最短路径长度为经过节点 k 的路径长度。
-
重复执行步骤 2:重复执行步骤 2,直到所有节点对之间的最短路径长度都被计算出来,即距离矩阵不再变化。
-
输出结果:输出距离矩阵,其中的每个元素表示对应节点对之间的最短路径长度。
弗洛伊德算法的核心思想是动态规划。通过逐步迭代更新节点对之间的最短路径长度,算法最终得到所有节点对之间的最短路径。由于需要遍历所有节点和中间节点,算法的时间复杂度为 O(n^3),其中 n 是图中节点的数量。
总的来说就是,建模+核心的3个for循环
for (int k = 1; k <= n; k++) // 这个是中间途经的点{for (int i = 1; i <= n; i++) { // 起始点for (int j = 1; j <= n; j++) { // 终点d[i][j] = min(d[i][j], d[i][k] + d[k][j]);}}}
最终实现的代码如下
#include<iostream>using namespace std;
typedef long long ll;const int N = 410;
ll d[N][N]; // 开辟一个数组存储信息int n, m, q; // 设置全局变量void floyd()
{for (int k = 1; k <= n; k++){for (int i = 1; i <= n; i++) {for (int j = 1; j <= n; j++) {d[i][j] = min(d[i][j], d[i][k] + d[k][j]);}}}
}int main()
{cin >> n >> m >> q;// 下面要进行初始化操作for (int i = 1; i <= n; i++) {for (int j = 1; j <= n; j++) {if (i == j) d[i][j] = 0;else d[i][j] = LLONG_MAX / 2;}}while (m--){ll a, b, c;cin >> a >> b >> c;d[a][b] = d[b][a] = min(d[a][b], c);}floyd();while (q--){int a, b;cin >> a >> b;if (d[a][b] >= LLONG_MAX / 2) cout << "-1" << endl;else cout << d[a][b] << endl;}return 0;
}有一个小细节,初始化数组的时候
d[a][b] = d[b][a] = min(d[a][b], c);
这个要避免有重边
相关文章:

蓝桥杯备战 每日一题 (2)
今天的题目是回忆迷宫 这个题目我们来熟悉一下 弗洛伊德算法 的代码模板 弗洛伊德算法用来处理最短路径问题 弗洛伊德算法(Floyd’s algorithm)用于解决图中所有节点对之间的最短路径问题。算法的基本思路是通过逐步迭代更新节点对之间的最短路径长度&a…...

GetShell的姿势
0x00 什么是WebShell 渗透测试工作的一个阶段性目标就是获取目标服务器的操作控制权限,于是WebShell便应运而生。Webshell中的WEB就是web服务,shell就是管理攻击者与操作系统之间的交互。Webshell被称为攻击者通过Web服务器端口对Web服务器有一定的操作权…...

workflow源码解析:ThreadTask
1、使用程序,一个简单的加法运算程序 #include <iostream> #include <workflow/WFTaskFactory.h> #include <errno.h>// 直接定义thread_task三要素 // 一个典型的后端程序由三个部分组成,并且完全独立开发。即:程序协议算…...

为何谷歌强制要求安装ssl证书?
在当今数字化的世界中,网络安全已成为至关重要的议题之一。作为全球最大的搜索引擎之一,谷歌一直在推动网络安全标准的提升。其强制要求网站安装SSL证书的决策引起了广泛关注。本文将深入探讨谷歌为何强制要求安装SSL证书,以及这一举措对互联…...
【刷题】 leetcode 2 .两数相加
两数相加 两数相加1 思路一 (暴毙版)2 思路二 (本质出发) 谢谢阅读Thanks♪(・ω・)ノ下一篇文章见!!!!!! 两数相加 我们来看…...

Webpack5入门到原理2:基本使用
Webpack 是一个静态资源打包工具。 它会以一个或多个文件作为打包的入口,将我们整个项目所有文件编译组合成一个或多个文件输出出去。 输出的文件就是编译好的文件,就可以在浏览器段运行了。 我们将 Webpack 输出的文件叫做 bundle。 功能介绍 Webp…...

企业微信上传临时素材errcode:44001,errmsg:empty media data
企业微信,上传临时素材,报错: {“errcode”:44001,“errmsg”:“empty media data [logid:]”}, 开发语言C# 重点代码: formData.Headers.ContentType new MediaTypeHeaderValue(“application/octet-stream”); 解…...
Docker技巧汇总
Docker技巧汇总 前言使用流程安装配置镜像管理创建并运行容器使用容器/常用命令导出和导入查看元数据挂载数据卷端口映射/转发VS Code连接Docker 前言 Docker 是一个开源的应用容器引擎,可以让开发者打包他们的应用以及依赖包到一个轻量级、可移植的容器中…...

学习使用微信小程序实现智能名片电子名片功能代码
学习使用微信小程序实现智能名片电子名片功能代码 拨打手机号功能一键复制信息功能定位导航功能存入手机通讯录功能转发分享功能 拨打手机号功能 wx.makePhoneCall({phoneNumber: qipa250 //仅为示例,并非真实的电话号码 })一键复制信息功能 wx.getClipboardData(…...
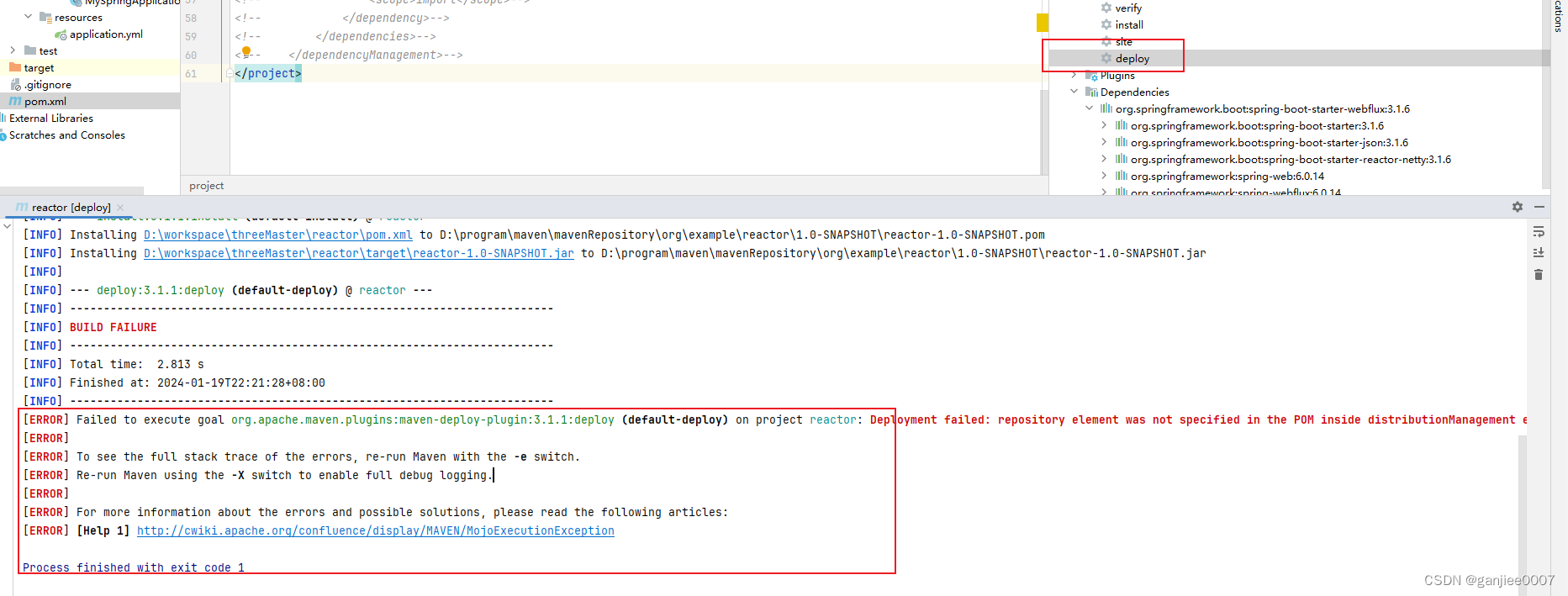
学习响应式编程中遇到的奇奇怪怪的问题
spring项目无法启动 Description: Web application could not be started as there was no org.springframework.boot.web.reactive.server.ReactiveWebServerFactory bean defined in the context. Action: Check your application’s dependencies for a supported react…...

前端常用js、css效果
前端常用js效果 效果参考代码文本横向滚动文本无限滚动无缝轮播无缝滚动盒子上下移动樱花飘落 效果 主要整理了几个常用的,方便平时做项目的时候参考 文本横向滚动 文本无限滚动 无缝轮播 无缝滚动 盒子上下滚动 樱花飘落效果 参考代码 文本横向滚动 <!DOCTYP…...
Modern C++ 条件变量
今天无意中看到一篇帖子,关于条件变量的,不过仔细看看发现它并达不到原本的目的。 程序如下,读者可以先想想他的本意,以及有没有问题: #include <iostream> #include <thread> #include <condition_v…...

免费chartGPT网站汇总--
https://s.suolj.com - (支持文心、科大讯飞、智谱等国内大语言模型,Midjourney绘画、语音对讲、聊天插件)国内可以直连,响应速度很快 很稳定 https://seboai.github.io - 国内可以直连,响应速度很快 很稳定 http://gp…...
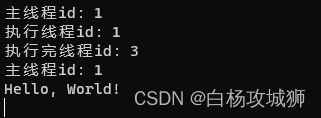
关于C#中的async/await的理解
1. 使用async标记的方法被认为是一个异步方法,如果不使用await关键字,调用跟普通方法没有区别 static async Task Main(string[] args){Console.WriteLine("主线程id:" Thread.CurrentThread.ManagedThreadId);TestAwait();Consol…...

docker硬件交互 _ROS2
docker硬件交互 _ROS2 将自己需要挂载的设备接到主板上,在宿主机中建立udev规则(/etc/udev/rules.d/)然后在开启容器时,将设置了规则的devices 通过 --device/dev/myserial --device/dev/rplidar 等 参数挂载到docker容器中 doc…...

JS的数据类型和运算符
typeof()方法:检测数据类型 JS中的基本数据类型 基本数据类型 1.number 数字 2.string 字符串 3.boolean 布尔 4.null 代表空值(typeof方法检测出来的数据类型是object类型) 5.underfined 未定义;变量已声明但是未赋值 6.…...

CSS实现平行四边形
1、为什么实现平行四边形 在日常开发过程中,有些时候我们可以会遇到一种情况,如可视化大屏中要求我们横线实现对应的进度条,但进度条的内容是由无数个平行四边形组装类似于进度条的形式,那么我们就需要使用CSS来进行对应的实现。 …...
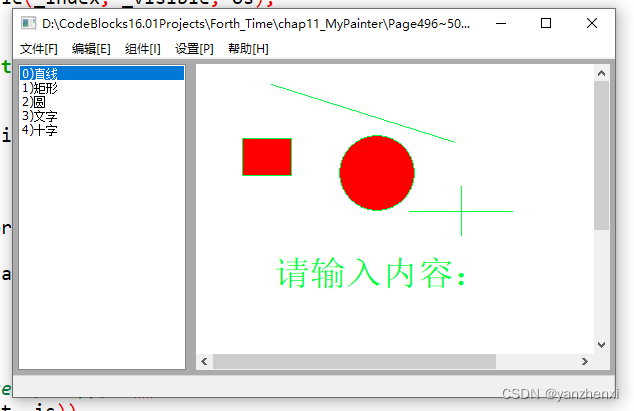
第11章 GUI Page500~504 步骤三十二:打开画板文件02
各个图元类新增GetTypeName_Static(),并将原来的GetTypeName()改为调用静态方法实现: 直线: 圆: 十字: 矩形: 文字: tool_4_save_load.hpp添加两行 tool_4_save_load.cpp增加: 增加…...

【ROS2】ROS2使用C++实现简单服务端
使用ROS2实现简单的服务端,功能为将客户端提供的两个数相加后返回给客户端。 代码如下: #include "rclcpp/rclcpp.hpp" #include "std_msgs/msg/string.hpp" #include "base_interfaces_demo/msg/student.hpp" #include "base_interfac…...
WAF攻防相关知识点总结1--信息收集中的WAF触发及解决方案
什么是WAF WAF可以通过对Web应用程序的流量进行过滤和监控,识别并阻止潜在的安全威胁。WAF可以检测Web应用程序中的各种攻击,例如SQL注入、跨站点脚本攻击(XSS)、跨站请求伪造(CSRF)等,并采取相…...

TDengine 快速体验(Docker 镜像方式)
简介 TDengine 可以通过安装包、Docker 镜像 及云服务快速体验 TDengine 的功能,本节首先介绍如何通过 Docker 快速体验 TDengine,然后介绍如何在 Docker 环境下体验 TDengine 的写入和查询功能。如果你不熟悉 Docker,请使用 安装包的方式快…...
)
椭圆曲线密码学(ECC)
一、ECC算法概述 椭圆曲线密码学(Elliptic Curve Cryptography)是基于椭圆曲线数学理论的公钥密码系统,由Neal Koblitz和Victor Miller在1985年独立提出。相比RSA,ECC在相同安全强度下密钥更短(256位ECC ≈ 3072位RSA…...

visual studio 2022更改主题为深色
visual studio 2022更改主题为深色 点击visual studio 上方的 工具-> 选项 在选项窗口中,选择 环境 -> 常规 ,将其中的颜色主题改成深色 点击确定,更改完成...

FastAPI 教程:从入门到实践
FastAPI 是一个现代、快速(高性能)的 Web 框架,用于构建 API,支持 Python 3.6。它基于标准 Python 类型提示,易于学习且功能强大。以下是一个完整的 FastAPI 入门教程,涵盖从环境搭建到创建并运行一个简单的…...

Auto-Coder使用GPT-4o完成:在用TabPFN这个模型构建一个预测未来3天涨跌的分类任务
通过akshare库,获取股票数据,并生成TabPFN这个模型 可以识别、处理的格式,写一个完整的预处理示例,并构建一个预测未来 3 天股价涨跌的分类任务 用TabPFN这个模型构建一个预测未来 3 天股价涨跌的分类任务,进行预测并输…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个生活电费的缴纳和查询小程序
一、项目初始化与配置 1. 创建项目 ohpm init harmony/utility-payment-app 2. 配置权限 // module.json5 {"requestPermissions": [{"name": "ohos.permission.INTERNET"},{"name": "ohos.permission.GET_NETWORK_INFO"…...

【C语言练习】080. 使用C语言实现简单的数据库操作
080. 使用C语言实现简单的数据库操作 080. 使用C语言实现简单的数据库操作使用原生APIODBC接口第三方库ORM框架文件模拟1. 安装SQLite2. 示例代码:使用SQLite创建数据库、表和插入数据3. 编译和运行4. 示例运行输出:5. 注意事项6. 总结080. 使用C语言实现简单的数据库操作 在…...

鱼香ros docker配置镜像报错:https://registry-1.docker.io/v2/
使用鱼香ros一件安装docker时的https://registry-1.docker.io/v2/问题 一键安装指令 wget http://fishros.com/install -O fishros && . fishros出现问题:docker pull 失败 网络不同,需要使用镜像源 按照如下步骤操作 sudo vi /etc/docker/dae…...

tree 树组件大数据卡顿问题优化
问题背景 项目中有用到树组件用来做文件目录,但是由于这个树组件的节点越来越多,导致页面在滚动这个树组件的时候浏览器就很容易卡死。这种问题基本上都是因为dom节点太多,导致的浏览器卡顿,这里很明显就需要用到虚拟列表的技术&…...

鸿蒙DevEco Studio HarmonyOS 5跑酷小游戏实现指南
1. 项目概述 本跑酷小游戏基于鸿蒙HarmonyOS 5开发,使用DevEco Studio作为开发工具,采用Java语言实现,包含角色控制、障碍物生成和分数计算系统。 2. 项目结构 /src/main/java/com/example/runner/├── MainAbilitySlice.java // 主界…...
