openssl3.2 - 官方demo学习 - pkey - EVP_PKEY_RSA_keygen.c
文章目录
- openssl3.2 - 官方demo学习 - pkey - EVP_PKEY_RSA_keygen.c
- 概述
- 笔记
- END
openssl3.2 - 官方demo学习 - pkey - EVP_PKEY_RSA_keygen.c
概述
官方指出 : RSA key 如果小于2048位, 就属于弱key
官方demo中, 给出的默认key长度为4096位
从名字生成上下文
初始化上下文
设置上下的key位数
设置质数数量为2
产生RSA Key. (在我的本本上, 单步调试时, 感觉产生 RSA key时, 卡了一下, 大概不到1秒钟)
打印rsa key内容(可以得到 n, e, d, p, q, key的位数, 公钥, 私钥)
PEM_write_x时, 如果文件句柄是具体的文件, 就是将公钥/密钥保存成了PEM文件.
笔记
/*!
\file EVP_PKEY_RSA_keygen.c
\note
openssl3.2 - 官方demo学习 - pkey - EVP_PKEY_RSA_keygen.c官方指出 : RSA key 如果小于2048位, 就属于弱key
官方demo中, 给出的默认key长度为4096位从名字生成上下文
初始化上下文
设置上下的key位数
设置质数数量为2
产生RSA Key. (在我的本本上, 单步调试时, 感觉产生 RSA key时, 卡了一下, 大概不到1秒钟)
打印rsa key内容(可以得到 n, e, d, p, q, key的位数, 公钥, 私钥)
PEM_write_x时, 如果文件句柄是具体的文件, 就是将公钥/密钥保存成了PEM文件.
*//*-* Copyright 2022-2023 The OpenSSL Project Authors. All Rights Reserved.** Licensed under the Apache License 2.0 (the "License"). You may not use* this file except in compliance with the License. You can obtain a copy* in the file LICENSE in the source distribution or at* https://www.openssl.org/source/license.html*//** Example showing how to generate an RSA key pair.** When generating an RSA key, you must specify the number of bits in the key. A* reasonable value would be 4096. Avoid using values below 2048. These values* are reasonable as of 2022.*/#include <string.h>
#include <stdio.h>
#include <openssl/err.h>
#include <openssl/evp.h>
#include <openssl/rsa.h>
#include <openssl/core_names.h>
#include <openssl/pem.h>#include "my_openSSL_lib.h"/* A property query used for selecting algorithm implementations. */
static const char* propq = NULL;/** Generates an RSA public-private key pair and returns it.* The number of bits is specified by the bits argument.** This uses the long way of generating an RSA key.*/
static EVP_PKEY* generate_rsa_key_long(OSSL_LIB_CTX* libctx, unsigned int bits)
{EVP_PKEY_CTX* genctx = NULL;EVP_PKEY* pkey = NULL;unsigned int primes = 2;/* Create context using RSA algorithm. "RSA-PSS" could also be used here. */genctx = EVP_PKEY_CTX_new_from_name(libctx, "RSA", propq);if (genctx == NULL) {fprintf(stderr, "EVP_PKEY_CTX_new_from_name() failed\n");goto cleanup;}/* Initialize context for key generation purposes. */if (EVP_PKEY_keygen_init(genctx) <= 0) {fprintf(stderr, "EVP_PKEY_keygen_init() failed\n");goto cleanup;}/** Here we set the number of bits to use in the RSA key.* See comment at top of file for information on appropriate values.*/if (EVP_PKEY_CTX_set_rsa_keygen_bits(genctx, bits) <= 0) {fprintf(stderr, "EVP_PKEY_CTX_set_rsa_keygen_bits() failed\n");goto cleanup;}/** It is possible to create an RSA key using more than two primes.* Do not do this unless you know why you need this.* You ordinarily do not need to specify this, as the default is two.** Both of these parameters can also be set via EVP_PKEY_CTX_set_params, but* these functions provide a more concise way to do so.*/if (EVP_PKEY_CTX_set_rsa_keygen_primes(genctx, primes) <= 0) {fprintf(stderr, "EVP_PKEY_CTX_set_rsa_keygen_primes() failed\n");goto cleanup;}/** Generating an RSA key with a number of bits large enough to be secure for* modern applications can take a fairly substantial amount of time (e.g.* one second). If you require fast key generation, consider using an EC key* instead.** If you require progress information during the key generation process,* you can set a progress callback using EVP_PKEY_set_cb; see the example in* EVP_PKEY_generate(3).*/fprintf(stderr, "Generating RSA key, this may take some time...\n");if (EVP_PKEY_generate(genctx, &pkey) <= 0) {fprintf(stderr, "EVP_PKEY_generate() failed\n");goto cleanup;}/* pkey is now set to an object representing the generated key pair. */cleanup:EVP_PKEY_CTX_free(genctx);return pkey;
}/** Generates an RSA public-private key pair and returns it.* The number of bits is specified by the bits argument.** This uses a more concise way of generating an RSA key, which is suitable for* simple cases. It is used if -s is passed on the command line, otherwise the* long method above is used. The ability to choose between these two methods is* shown here only for demonstration; the results are equivalent.*/
static EVP_PKEY* generate_rsa_key_short(OSSL_LIB_CTX* libctx, unsigned int bits)
{EVP_PKEY* pkey = NULL;fprintf(stderr, "Generating RSA key, this may take some time...\n");pkey = EVP_PKEY_Q_keygen(libctx, propq, "RSA", (size_t)bits);if (pkey == NULL)fprintf(stderr, "EVP_PKEY_Q_keygen() failed\n");return pkey;
}/** Prints information on an EVP_PKEY object representing an RSA key pair.*/
static int dump_key(const EVP_PKEY* pkey)
{int ret = 0;int bits = 0;BIGNUM* n = NULL, * e = NULL, * d = NULL, * p = NULL, * q = NULL;/** Retrieve value of n. This value is not secret and forms part of the* public key.** Calling EVP_PKEY_get_bn_param with a NULL BIGNUM pointer causes* a new BIGNUM to be allocated, so these must be freed subsequently.*/if (EVP_PKEY_get_bn_param(pkey, OSSL_PKEY_PARAM_RSA_N, &n) == 0) {fprintf(stderr, "Failed to retrieve n\n");goto cleanup;}/** Retrieve value of e. This value is not secret and forms part of the* public key. It is typically 65537 and need not be changed.*/if (EVP_PKEY_get_bn_param(pkey, OSSL_PKEY_PARAM_RSA_E, &e) == 0) {fprintf(stderr, "Failed to retrieve e\n");goto cleanup;}/** Retrieve value of d. This value is secret and forms part of the private* key. It must not be published.*/if (EVP_PKEY_get_bn_param(pkey, OSSL_PKEY_PARAM_RSA_D, &d) == 0) {fprintf(stderr, "Failed to retrieve d\n");goto cleanup;}/** Retrieve value of the first prime factor, commonly known as p. This value* is secret and forms part of the private key. It must not be published.*/if (EVP_PKEY_get_bn_param(pkey, OSSL_PKEY_PARAM_RSA_FACTOR1, &p) == 0) {fprintf(stderr, "Failed to retrieve p\n");goto cleanup;}/** Retrieve value of the second prime factor, commonly known as q. This value* is secret and forms part of the private key. It must not be published.** If you are creating an RSA key with more than two primes for special* applications, you can retrieve these primes with* OSSL_PKEY_PARAM_RSA_FACTOR3, etc.*/if (EVP_PKEY_get_bn_param(pkey, OSSL_PKEY_PARAM_RSA_FACTOR2, &q) == 0) {fprintf(stderr, "Failed to retrieve q\n");goto cleanup;}/** We can also retrieve the key size in bits for informational purposes.*/if (EVP_PKEY_get_int_param(pkey, OSSL_PKEY_PARAM_BITS, &bits) == 0) {fprintf(stderr, "Failed to retrieve bits\n");goto cleanup;}/* Output hexadecimal representations of the BIGNUM objects. */fprintf(stdout, "\nNumber of bits: %d\n\n", bits);fprintf(stderr, "Public values:\n");fprintf(stdout, " n = 0x");BN_print_fp(stdout, n);fprintf(stdout, "\n");fprintf(stdout, " e = 0x");BN_print_fp(stdout, e);fprintf(stdout, "\n\n");fprintf(stdout, "Private values:\n");fprintf(stdout, " d = 0x");BN_print_fp(stdout, d);fprintf(stdout, "\n");fprintf(stdout, " p = 0x");BN_print_fp(stdout, p);fprintf(stdout, "\n");fprintf(stdout, " q = 0x");BN_print_fp(stdout, q);fprintf(stdout, "\n\n");/* Output a PEM encoding of the public key. */if (PEM_write_PUBKEY(stdout, pkey) == 0) {fprintf(stderr, "Failed to output PEM-encoded public key\n");goto cleanup;}/** Output a PEM encoding of the private key. Please note that this output is* not encrypted. You may wish to use the arguments to specify encryption of* the key if you are storing it on disk. See PEM_write_PrivateKey(3).*/if (PEM_write_PrivateKey(stdout, pkey, NULL, NULL, 0, NULL, NULL) == 0) {fprintf(stderr, "Failed to output PEM-encoded private key\n");goto cleanup;}ret = 1;
cleanup:BN_free(n); /* not secret */BN_free(e); /* not secret */BN_clear_free(d); /* secret - scrub before freeing */BN_clear_free(p); /* secret - scrub before freeing */BN_clear_free(q); /* secret - scrub before freeing */return ret;
}int main(int argc, char** argv)
{int ret = EXIT_FAILURE;OSSL_LIB_CTX* libctx = NULL;EVP_PKEY* pkey = NULL;unsigned int bits = 4096;int bits_i, use_short = 0;/* usage: [-s] [<bits>] */if (argc > 1 && strcmp(argv[1], "-s") == 0) {--argc;++argv;use_short = 1;}if (argc > 1) {bits_i = atoi(argv[1]);if (bits < 512) {fprintf(stderr, "Invalid RSA key size\n");return EXIT_FAILURE;}bits = (unsigned int)bits_i;}/* Avoid using key sizes less than 2048 bits; see comment at top of file. */if (bits < 2048)fprintf(stderr, "Warning: very weak key size\n\n");/* Generate RSA key. */if (use_short)pkey = generate_rsa_key_short(libctx, bits);elsepkey = generate_rsa_key_long(libctx, bits);if (pkey == NULL)goto cleanup;/* Dump the integers comprising the key. */if (dump_key(pkey) == 0) {fprintf(stderr, "Failed to dump key\n");goto cleanup;}ret = EXIT_SUCCESS;
cleanup:EVP_PKEY_free(pkey);OSSL_LIB_CTX_free(libctx);return ret;
}END
相关文章:

openssl3.2 - 官方demo学习 - pkey - EVP_PKEY_RSA_keygen.c
文章目录 openssl3.2 - 官方demo学习 - pkey - EVP_PKEY_RSA_keygen.c概述笔记END openssl3.2 - 官方demo学习 - pkey - EVP_PKEY_RSA_keygen.c 概述 官方指出 : RSA key 如果小于2048位, 就属于弱key 官方demo中, 给出的默认key长度为4096位 从名字生成上下文 初始化上下文…...
密码搜|Facebook 8组问答,搞定Pixel与广告之间的关系!
Q1:Pixel(像素/代码)是什么? A:Pixel有多种称呼:Pixel、像素、代码。它只是一种分析工具,可帮助广告主了解用户在网站上采取的操作,继而衡量广告成效。 设置Facebook Pixel像素代码…...
Apache StringUtils:Java字符串处理工具类
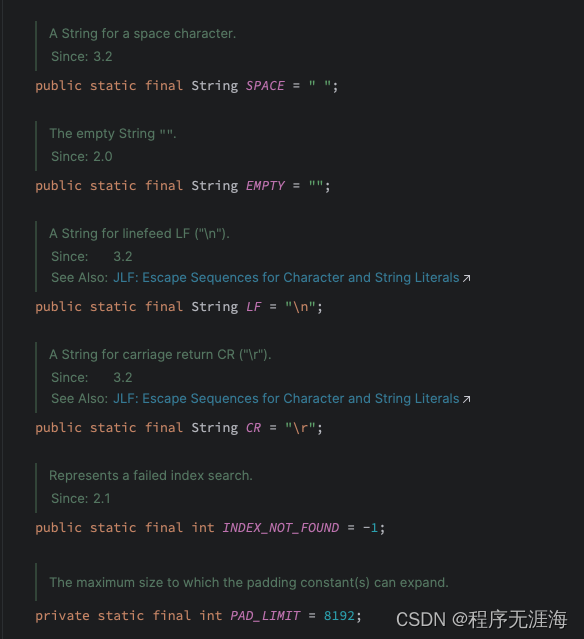
简介 在我们的代码中经常需要对字符串判空,截取字符串、转换大小写、分隔字符串、比较字符串、去掉多余空格、拼接字符串、使用正则表达式等等。如果只用 String 类提供的那些方法,我们需要手写大量的额外代码,不然容易出现各种异常。现在有…...
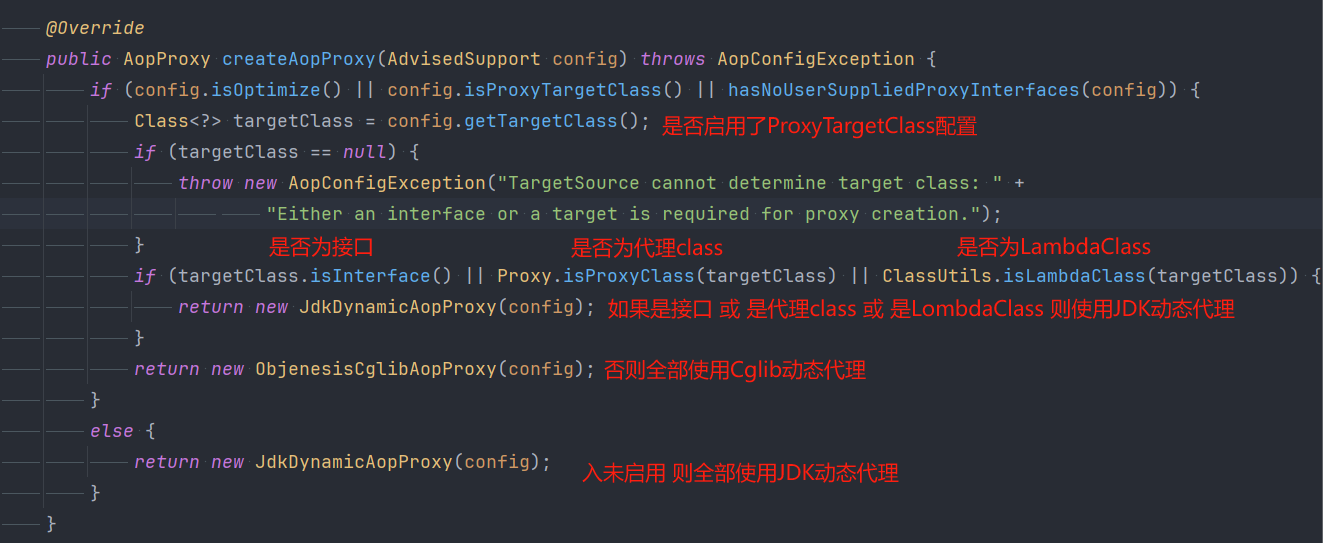
设计模式 代理模式(静态代理 动态代理) 与 Spring Aop源码分析 具体是如何创建Aop代理的
代理模式 代理模式是一种结构型设计模式,它通过创建一个代理对象来控制对真实对象的访问。这种模式可以用于提供额外的功能操作,或者扩展目标对象的功能。 在代理模式中,代理对象与真实对象实现相同的接口,以便在任何地方都可以使…...

【EI会议征稿通知】第七届先进电子材料、计算机与软件工程国际学术会议(AEMCSE 2024)
第七届先进电子材料、计算机与软件工程国际学术会议(AEMCSE 2024) 2024 7th International Conference on Advanced Electronic Materials, Computers and Software Engineering 第七届先进电子材料、计算机与软件工程国际学术会议(AEMCSE 2024)将于2024年5月10-1…...
Verilog基础:强度建模(一)
相关阅读 Verilog基础https://blog.csdn.net/weixin_45791458/category_12263729.html?spm1001.2014.3001.5482 一、强度建模基础 Verilog HDL提供了针对线网信号0、1、x、z的精准强度建模方式,这样可以允许将两个线网信号进行线与操作从而更加精确地描述出硬件行…...

Spring Boot各类变量的使用
文章目录 1. 变量类型2. 获取变量2.1 获取方式2.2 获取方法2.2.1 通过Value注入获取变量值2.2.2 System.genenv 获取变量值2.2.3 System.getProperty 获取变量值2.2.4 Environment 获取变量值2.2.5 ConfigurationProperties 获取变量值2.2.6 SpringApplication.run 程序启动参数…...

Hive管理UDF详解
大数据集群下,共有三种管理Hive UDF的方式,如下: 名称重启Hive服务Jar保存目录场景直接JAR配置需要HDFS开发辅助JARs目录配置需要本地目录防止意外覆盖文件可重载辅助JAR配置不需要本地目录频繁更新UDF场景{HIVE_HOME}/auxlib目录需要本地目录不建议{HIVE_HOME}/lib目录需要…...
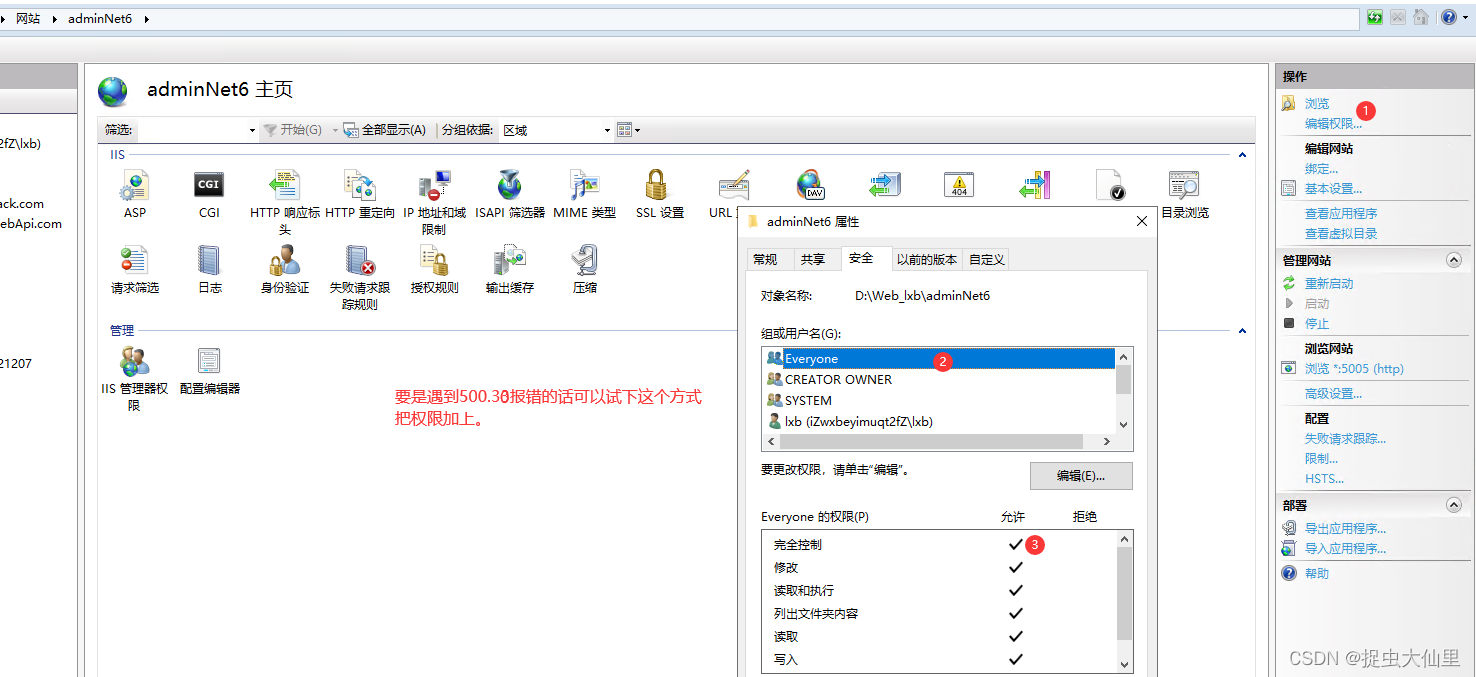
bug笔记:解决 HTTP Error 500.30 - ASP.NET Core app failed to start
总结下后端部署windos iis环境net6版本,500.30问题报错的一种解决方案: 一、问题描述 二、解决方案 检查下是否安装了net6对应的环境,是否已经安装 然后在事件管理器>Windows日志>应用程序,里面查看详细异常记录 在iis下面…...

理解pytorch系列:transpose是怎么实现的
在PyTorch中,transpose()是一种操作,它交换张量中两个指定维度的位置。实现这一点的关键在于不实际移动数据,而是通过改变张量的元数据(包括步长(stride)和尺寸(size))来…...
)
Linux tftp命令教程:文件传输利器(附案例详解和注意事项)
Linux tftp命令介绍 tftp,全称为Trivial File Transfer Protocol(简单文件传输协议)。tftp是一个用于文件传输的客户端命令,用于从远程主机传输文件,包括一些非常简洁、通常嵌入的系统。 Linux tftp命令适用的Linux版…...

beego的模块篇 - task任务
利用该工具来定时的做一些任务,但是有些时候我们的进程内也希望定时的来处理一些事情,可以使用crontab。 1 任务计划 1.1 初始化一个任务 tk1 : task.NewTask("tk1", "0 12 * * * *", func(ctx context.Context) error { fmt.Pri…...

ThreadLocal工具类
ThreadLocal工具类 ThreadLocalUtil.java public class ThreadLocalUtil {static final ThreadLocal THREAD_LOCAL new ThreadLocal();public static <T> T get() {return (T) THREAD_LOCAL.get();}public static void set(Object value) {THREAD_LOCAL.set(value);}p…...
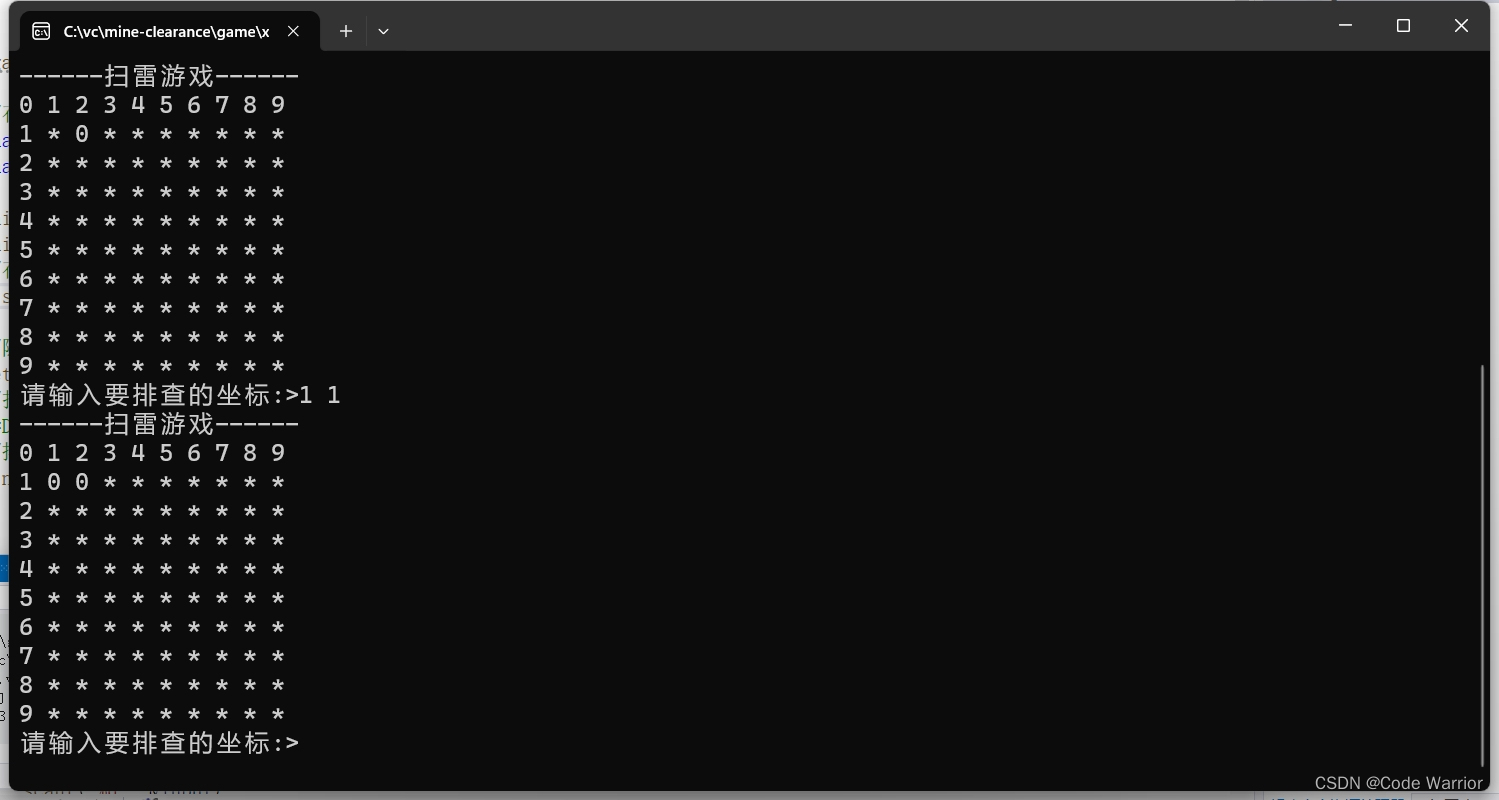
【c语言】扫雷(上)
先开一个test.c文件用来游戏的逻辑测试,在分别开一个game.c文件和game.h头文件用来实现游戏的逻辑 主要步骤: 游戏规则: 输入1(0)开始(结束)游戏,输入一个坐标,如果该坐…...

Java读取制表符文本转换为JSON
在Java开发中,处理各种数据格式是常见的任务。本文将介绍如何使用Java读取制表符文本文件,并将其转换为JSON格式,以便于后续的数据处理和分析。我们将使用Java中的相关库来实现这个过程,并提供详细的代码示例。 引言:…...

从C到C++:向面向对象过渡的技巧与诀窍
从C到C的过渡是一项对于程序员来说非常重要的转变。C是一种基于C语言的面向对象编程语言,它引入了许多新的概念和功能,如类、对象、继承和多态等。这些新的特性使得C在软件开发中更加灵活、可复用和易于维护。 下面是一些向面向对象过渡的技巧和诀窍&am…...

Vue3中动态组件使用
一,动态组件使用: 应用场景:动态绑定或切换组件 应用Vue3碎片: is 1.使用 a.组件A <div class"layout-base"><Button>红茶</Button> </div>a.组件B <div class"layout-base"&g…...
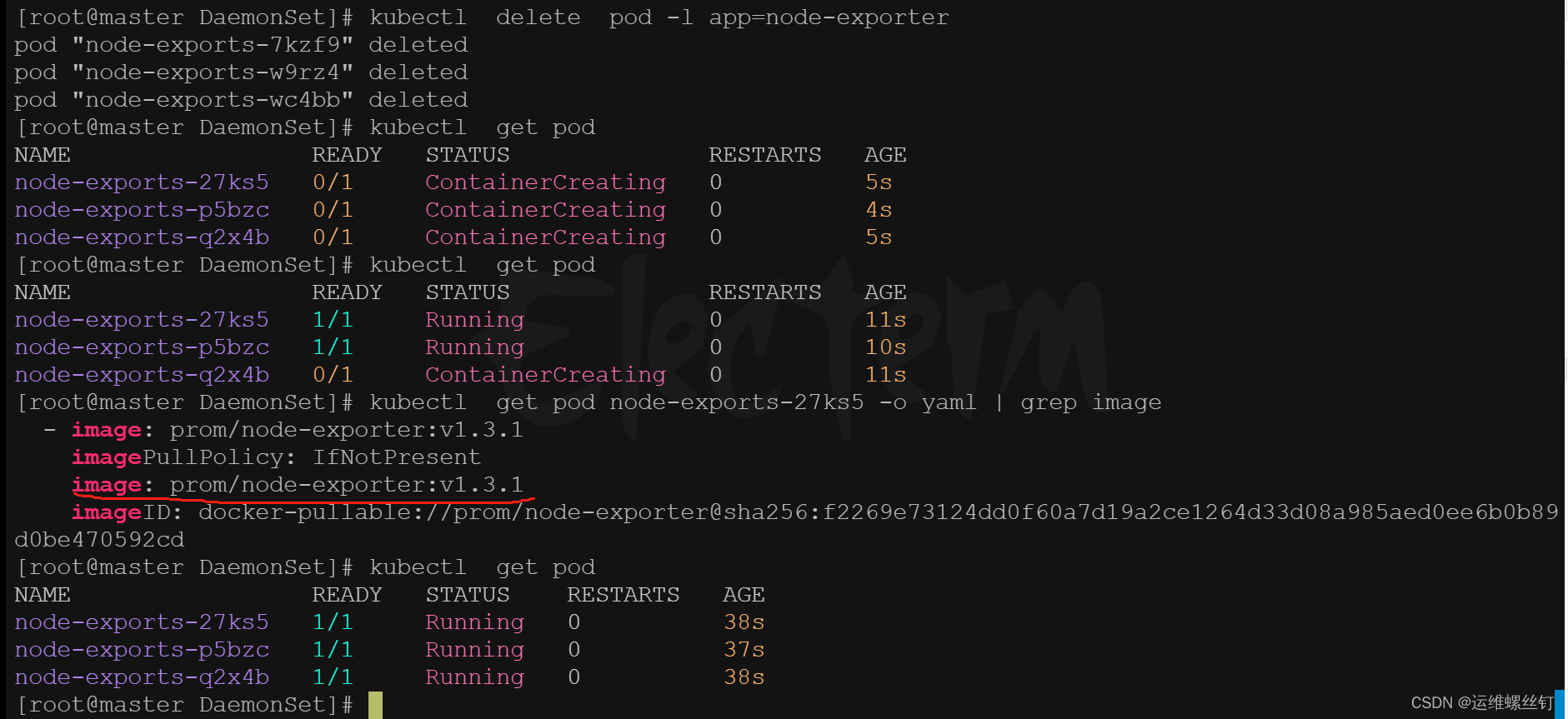
kubernetes工作负载-DamonSet
一、DemonSet的介绍 1、什么是DemonSet DaemonSet 控制器是用来保证在所有节点上运行一个 Pod 的副本当有节点加入集群时, 也会为他们新增一个 Pod。 当有节点从集群移除时,这些 Pod 也会被回收。删除 DaemonSet 将会删除它创建的所有 Pod。 简而言之…...

zabbix其他配置
自动发现 zabbix server 主动的去发现所有的客户端,然后将客户端的信息登记在服务端上。 缺点是如果定义的网段中的主机数量多,zabbix server 登记耗时较久,且压力会较大。 systemctl disable --now firewalld setenforce 0 hostnamectl se…...
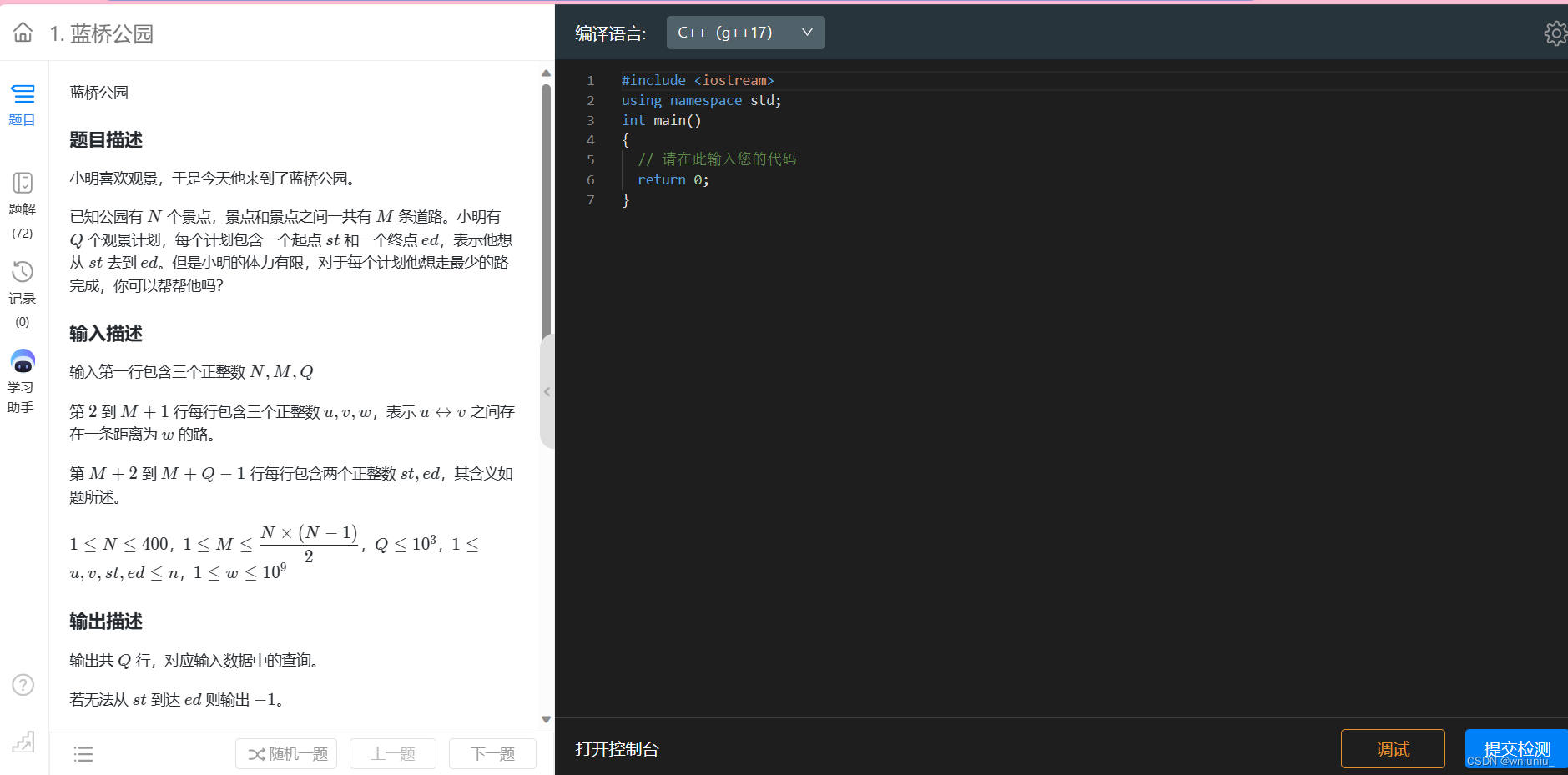
蓝桥杯备战 每日一题 (2)
今天的题目是回忆迷宫 这个题目我们来熟悉一下 弗洛伊德算法 的代码模板 弗洛伊德算法用来处理最短路径问题 弗洛伊德算法(Floyd’s algorithm)用于解决图中所有节点对之间的最短路径问题。算法的基本思路是通过逐步迭代更新节点对之间的最短路径长度&a…...

【杂谈】-递归进化:人工智能的自我改进与监管挑战
递归进化:人工智能的自我改进与监管挑战 文章目录 递归进化:人工智能的自我改进与监管挑战1、自我改进型人工智能的崛起2、人工智能如何挑战人类监管?3、确保人工智能受控的策略4、人类在人工智能发展中的角色5、平衡自主性与控制力6、总结与…...

练习(含atoi的模拟实现,自定义类型等练习)
一、结构体大小的计算及位段 (结构体大小计算及位段 详解请看:自定义类型:结构体进阶-CSDN博客) 1.在32位系统环境,编译选项为4字节对齐,那么sizeof(A)和sizeof(B)是多少? #pragma pack(4)st…...
)
IGP(Interior Gateway Protocol,内部网关协议)
IGP(Interior Gateway Protocol,内部网关协议) 是一种用于在一个自治系统(AS)内部传递路由信息的路由协议,主要用于在一个组织或机构的内部网络中决定数据包的最佳路径。与用于自治系统之间通信的 EGP&…...

基于uniapp+WebSocket实现聊天对话、消息监听、消息推送、聊天室等功能,多端兼容
基于 UniApp + WebSocket实现多端兼容的实时通讯系统,涵盖WebSocket连接建立、消息收发机制、多端兼容性配置、消息实时监听等功能,适配微信小程序、H5、Android、iOS等终端 目录 技术选型分析WebSocket协议优势UniApp跨平台特性WebSocket 基础实现连接管理消息收发连接…...
【机器视觉】单目测距——运动结构恢复
ps:图是随便找的,为了凑个封面 前言 在前面对光流法进行进一步改进,希望将2D光流推广至3D场景流时,发现2D转3D过程中存在尺度歧义问题,需要补全摄像头拍摄图像中缺失的深度信息,否则解空间不收敛…...

Python实现prophet 理论及参数优化
文章目录 Prophet理论及模型参数介绍Python代码完整实现prophet 添加外部数据进行模型优化 之前初步学习prophet的时候,写过一篇简单实现,后期随着对该模型的深入研究,本次记录涉及到prophet 的公式以及参数调优,从公式可以更直观…...

spring:实例工厂方法获取bean
spring处理使用静态工厂方法获取bean实例,也可以通过实例工厂方法获取bean实例。 实例工厂方法步骤如下: 定义实例工厂类(Java代码),定义实例工厂(xml),定义调用实例工厂ÿ…...

相机从app启动流程
一、流程框架图 二、具体流程分析 1、得到cameralist和对应的静态信息 目录如下: 重点代码分析: 启动相机前,先要通过getCameraIdList获取camera的个数以及id,然后可以通过getCameraCharacteristics获取对应id camera的capabilities(静态信息)进行一些openCamera前的…...

新能源汽车智慧充电桩管理方案:新能源充电桩散热问题及消防安全监管方案
随着新能源汽车的快速普及,充电桩作为核心配套设施,其安全性与可靠性备受关注。然而,在高温、高负荷运行环境下,充电桩的散热问题与消防安全隐患日益凸显,成为制约行业发展的关键瓶颈。 如何通过智慧化管理手段优化散…...

【Web 进阶篇】优雅的接口设计:统一响应、全局异常处理与参数校验
系列回顾: 在上一篇中,我们成功地为应用集成了数据库,并使用 Spring Data JPA 实现了基本的 CRUD API。我们的应用现在能“记忆”数据了!但是,如果你仔细审视那些 API,会发现它们还很“粗糙”:有…...
