【导航】繁星学习随想录
导航:繁星学习随想录
一、编程启示录
01 数据结构漫谈
| 序号 | 博文名称/链接 | |
|---|---|---|
| 01 | 扁扁笨算法-AVL树的插入与删除 | |
| 02 | 扁扁笨算法-B树的插入与删除 |
02 概念小扫盲
| 序号 | 博文名称/链接 | |
|---|---|---|
| 01 | 简单理解决策树_如何理解决策树的生长过程-CSDN博客 | |
| 02 | 白盒测试方法与黑盒测试方法简析_黑盒、白盒测试方案-CSDN博客 |
03 编程小车轮
| 序号 | 博文名称/链接 | |
|---|---|---|
| 01 | 编程启示录:图Graph的可视化方案 |
二、力扣风铃计划
| 序号 | 博文名称/链接 | |
|---|---|---|
| 01 | 编程启示录:栈的拿手好戏 | |
| 02 | 编程启示录:链表七怪 | |
| 03 | 二叉树的遍历大冒险 |
三、开发传习录
01 前端开发
| 序号 | 博文名称/链接 | |
|---|---|---|
| 01 |
02 后端开发
| 序号 | 博文名称/链接 | |
|---|---|---|
| 01 | 概念扫盲:Java中的几种对象_java 能使用的对象有那些-CSDN博客 |
03 前后端交互
| 序号 | 博文名称/链接 | |
|---|---|---|
| 01 | Ajax学习笔记-动力节点-王鹤老师_动力节点王鹤ajax笔记-CSDN博客 |
四、考研数学纪
01 高等数学笔记
| 序号 | 博文名称/链接 | |
|---|---|---|
| 01 | 高等数学笔记:等价无穷小巧记 | |
| 02 | 高等数学笔记:从导数定义视角的一个极限命题讨论 | |
| 03 | 高等数学笔记:连续与左右导数 | |
| 04 | 高等数学笔记:定积分换元谬误 | |
| 05 | 高等数学笔记:关于间断点的一些思考 | |
| 06 | 高等数学笔记:导函数与原函数关于函数性质的研究 | |
| 07 | 高等数学笔记:反常积分敛散性判别法 | |
| 08 | 高等数学笔记:两个重要的级数分析 | |
| 09 | 高等数学笔记:第一p广义积分与第二p广义积分 | |
| 10 | 高等数学笔记:极限的性质总结 | |
| 11 | 高等数学笔记:定积分相关公式 | |
| 12 | 高等数学笔记:中值定理【王下七武海】 | |
| 13 | 高等数学笔记:留数法-CSDN博客 | |
| 14 | 高等数学笔记:三角积分白银代换-CSDN博客 | |
| 15 | 高等数学笔记:三重积分下的坐标系变换 | |
| 16 | 高等数学笔记:幂级数 | |
| 17 | 高等数学笔记:泰勒公式分析——浅谈泰勒公式记忆背后的逻辑链条 | |
| 18 | 愤怒的导数:一点可导和邻域内可导能推出来什么? | |
| 19 | 高等数学笔记:傅里叶级数 | |
| 20 | 高等数学笔记:关于等价无穷小替换的一个猜想_武忠祥加减法无穷小替换原则-CSDN博客 | |
| 21 | 高等数学笔记:复合函数的二阶导数与参数方程求解曲率_复合函数 微商公式 二阶-CSDN博客 | |
| 22 | 高等数学笔记:三角积分星球_∫xdsinωx等于什么-CSDN博客 | |
| 23 | 高等数学笔记:泰勒展开求解渐近线_大一高数渐近线的求法例题-CSDN博客 | |
| 24 | 高等数学笔记:多元抽象复合函数求二阶偏导数_多元复合抽象函数 求导-CSDN博客 | |
| 25 | 高等数学笔记:二元微分极坐标在原点-CSDN博客 | |
| 26 | 高等数学笔记:旋转矩阵-CSDN博客 | |
| 27 | 高等数学笔记:三个糖葫芦-CSDN博客 | |
| 28 | 高等数学笔记:重积分的雅可比因子_雅克比因子-CSDN博客 | |
| 29 | 高等数学笔记:已知通解的微分方程-CSDN博客 |
02 线性代数笔记
| 序号 | 博文名称/链接 | |
|---|---|---|
| 01 | 线性代数让我想想:什么是秩?_秩是什么意思线性代数-CSDN博客 | |
| 02 | 线性代数让我想想:三阶行列式计算优化策略 | |
| 03 | 线性代数让我想想:克拉默法则 | |
| 04 | 线性代数让我想想:什么是秩? | |
| 05 | 线性代数让我想想:矩阵乘法的理解 | |
| 06 | 线性代数让我想想:简单理解非零矩阵相乘得零矩阵 | |
| 07 | 线性代数让我想想:快速求三阶矩阵的逆矩阵 | |
| 08 | 线性代数让我想想:两步得到二阶矩阵的逆 | |
| 09 | 线性代数让我想想:线性方程组的解 | |
| 10 | 线性代数让我想想:基础解系的个数为何是n-r | |
| 11 | 线性代数让我想想:特征值与特征向量 | |
| 12 | 线性代数让我想想:相似矩阵与矩阵的相似对角化 | |
| 13 | 线性代数笔记:从几何角度理解线性方程组 | |
| 14 | 线性代数笔记:左/右乘列/行满秩,秩不变 | |
| 15 | 线性代数笔记:花园小径行列式 | |
| 16 | 线性代数笔记:三阶矩阵的特征值计算 |
03 概率统计笔记
相关文章:

【导航】繁星学习随想录
导航:繁星学习随想录 一、编程启示录 01 数据结构漫谈 序号博文名称/链接01扁扁笨算法-AVL树的插入与删除02扁扁笨算法-B树的插入与删除 02 概念小扫盲 序号博文名称/链接01简单理解决策树_如何理解决策树的生长过程-CSDN博客02白盒测试方法与黑盒测试方法简析…...

Oracle 隐式数据类型转换
目录 Oracle类型转换规则: 看如下实验: 1、创建一张表,字段id的类型为number,id字段创建索引,插入一条测试数据 2、我们做如下查询,id的值设置为字符型的1 3、查看执行计划: Oracle类型转换…...
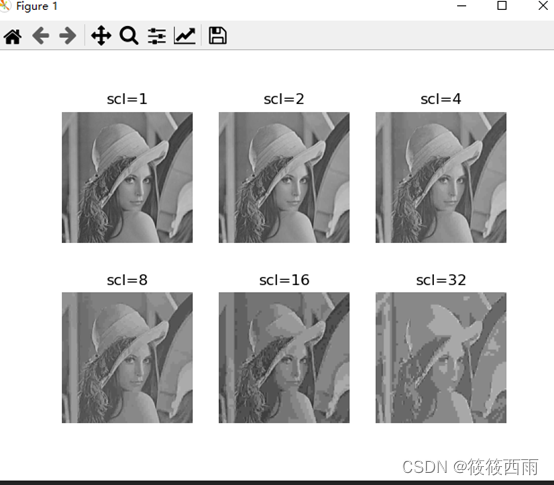
压缩编码之不同缩放参数对重建图像质量的影响的python实现——JPEG变换编码不同压缩率的模拟
原理 JPEG(Joint Photographic Experts Group)是一种常用的图像压缩标准,它通过采用离散余弦变换(DCT)和量化来实现图像的压缩。 离散余弦变换(DCT): JPEG首先将图像分割成8x8的块…...

大数据导论(2)---大数据与云计算、物联网、人工智能
文章目录 1. 云计算1.1 云计算概念1.2 云计算的服务模式和类型1.3 云计算的数据中心与应用 2. 物联网2.1 物联网的概念和关键技术2.2 物联网的应用和产业2.3 大数据与云计算、物联网的关系 1. 云计算 1.1 云计算概念 1. 首先从商业角度给云计算下一个定义:通过网络…...
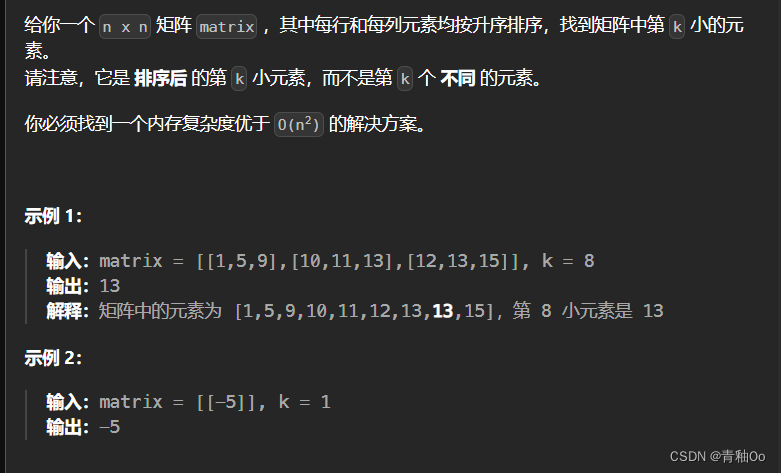
有序矩阵中第 K 小的元素
题目链接 有序矩阵中第 K 小的元素 题目描述 注意点 每行和每列元素均按升序排序找到一个内存复杂度优于 O(n) 的解决方案 解答思路 使用二分查找,思路为: (1)因为左上角的元素值更小,右下角的元素值更大…...

Nginx详细介绍(并从技术层面深度剖析)
nginx介绍 1.nginx 介绍2.nginx的优势3.Nginx VS Apache3.1.内核、语言、诞生时间比较3.2.功能比较3.3.Nginx 相对 apache 的优点 4.Nginx为什么有这么多的优势?4.1.IO多路复用(I/O multiplexing【多并发】)4.2.nginx的驱动模型介绍4.3.nginx…...

单元测试基本概念
单元测试一般是开发来做的,但是因为业务需要也曾涉及过单元测试。目前就单元测试的基础概念做下总结。 一、 单元测试定义: 单元测试是软件开发中的一种测试方法,用于验证程序中的最小可测单元——即代码中的单个函数、方法或模块。单元测试…...
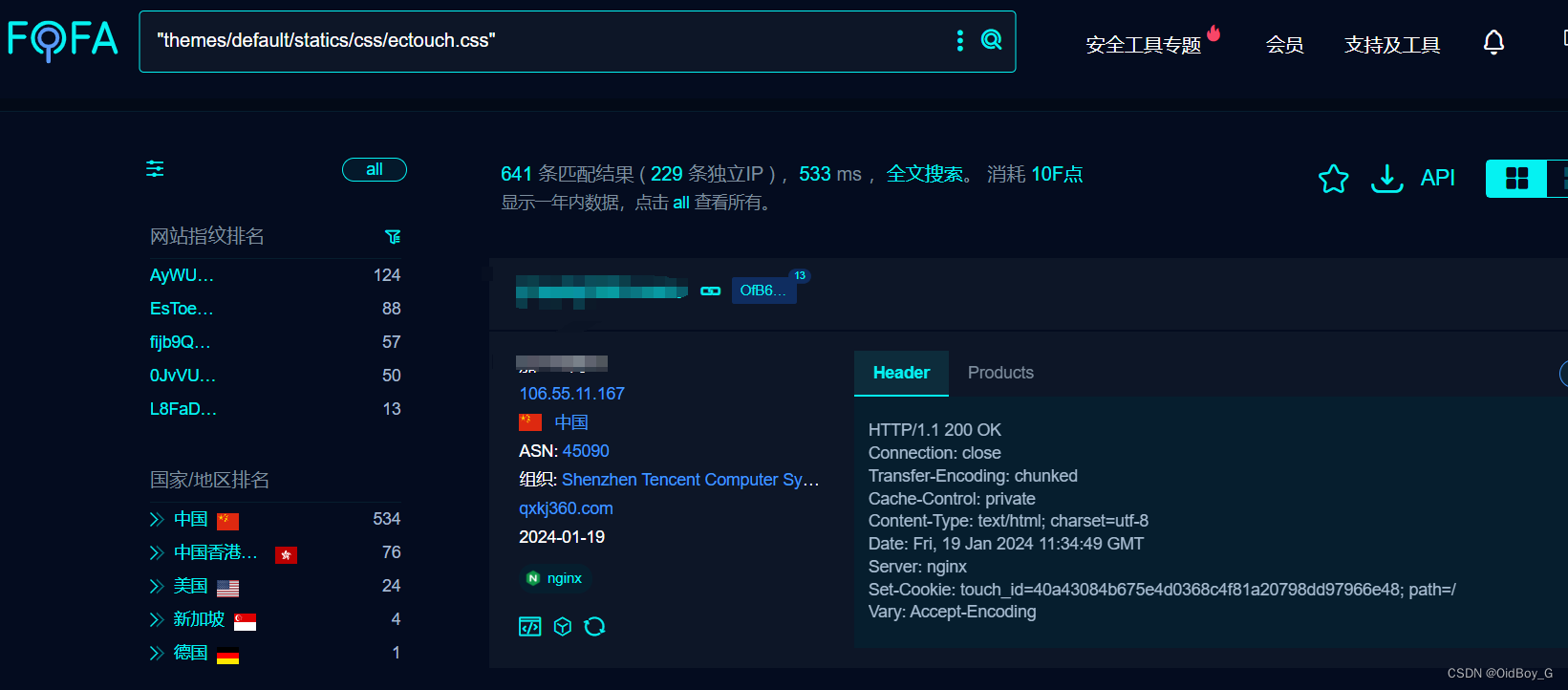
ECTouch 电商微信小程序 SQL注入漏洞复现(CVE-2023-39560)
0x01 产品简介 ECTouch是一款开源的电商系统,为中小企业提供最佳的新零售解决方案 0x02 漏洞概述 ECTouch 电商系统 /ectouch-main/include/apps/default/helpers/insert.php 文件中第285行的 insert_bought_notes 函数中,传入的 $arr[id] 参数未进行验证和过滤,导致未经…...
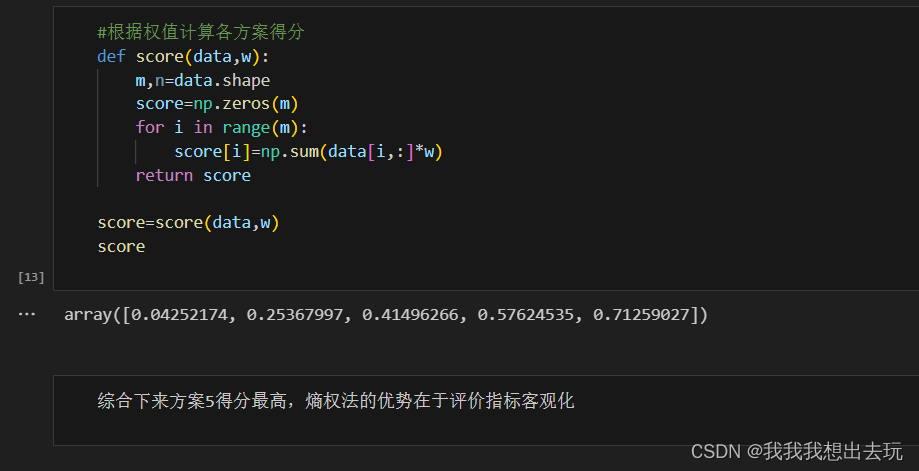
MCM备赛笔记——熵权法
Key Concept 熵权法是一种基于信息熵概念的权重确定方法,用于多指标决策分析中。信息熵是度量信息量的不确定性或混乱程度的指标,在熵权法中,它用来反映某个指标在评价过程中的分散程度,进而确定该指标的权重。指标的分散程度越高…...
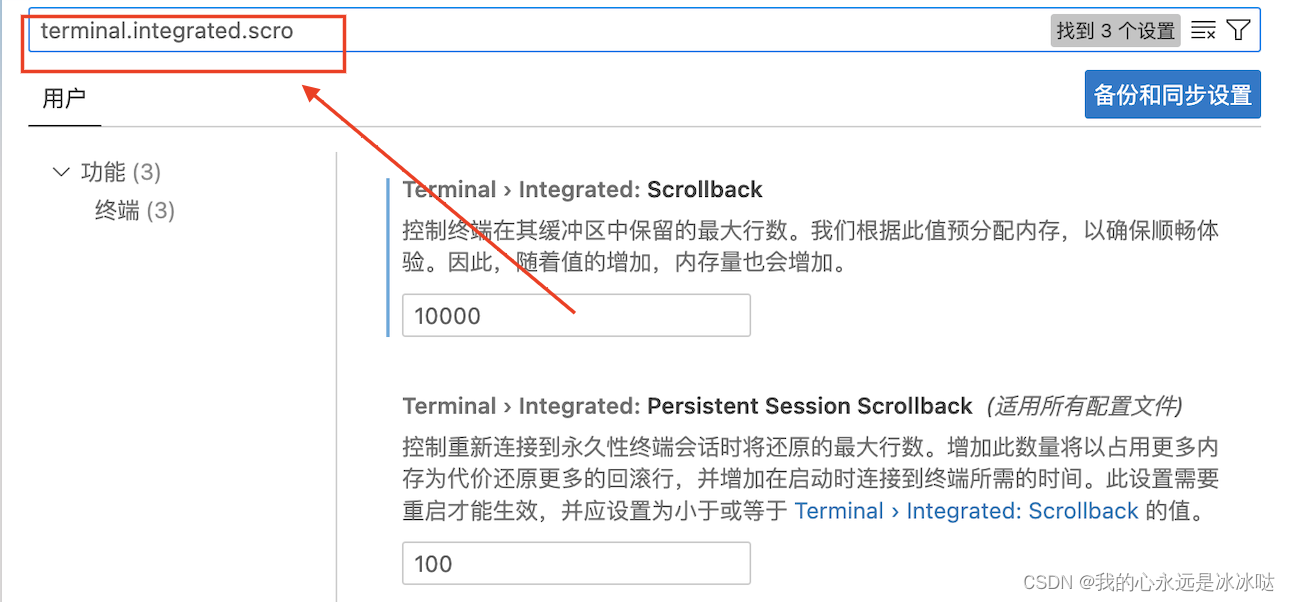
vscode设置terminal的最大行数
今天跑代码出现一个问题,就是整个程序跑完,整个程序的输出信息过多,最开始输出的信息已经被vscode的缓存冲掉了,只能看到最后的一部分,具体的原因是vscode的terminal默认只能保存1000行的信息,所以如果想保…...

kafka hang 问题记录
参考文档 https://cloud.tencent.com/developer/article/1821477 9092端口 端口9092通常与Apache Kafka关联。 Kafka是一个开源的分布式事件流平台,用于构建实时的数据管道和流应用。 它能够处理任意大小的数据,以容错的方式处理数据流。 在默认配置…...

Jmeter-BeanShell脚本中for循环里面使用random随机数函数,每次生成的都一样
预想的是每次循环生成的随机数不一样,但实际使用Random函数生成的是重复的。 以下是部分原代码: List updateList new ArrayList(); for(Object o: fieldList){Map map new HashMap();map.put("id", o.get("id"));map.put("…...

高级编程。JavaScript中有哪些类型转换机制?
一、概述 前面我们讲到,JS中有六种简单数据类型:undefined、null、boolean、string、number、symbol,以及引用类型:object 但是我们在声明的时候只有一种数据类型,只有到运行期间才会确定当前类型 let x y ? 1 : …...
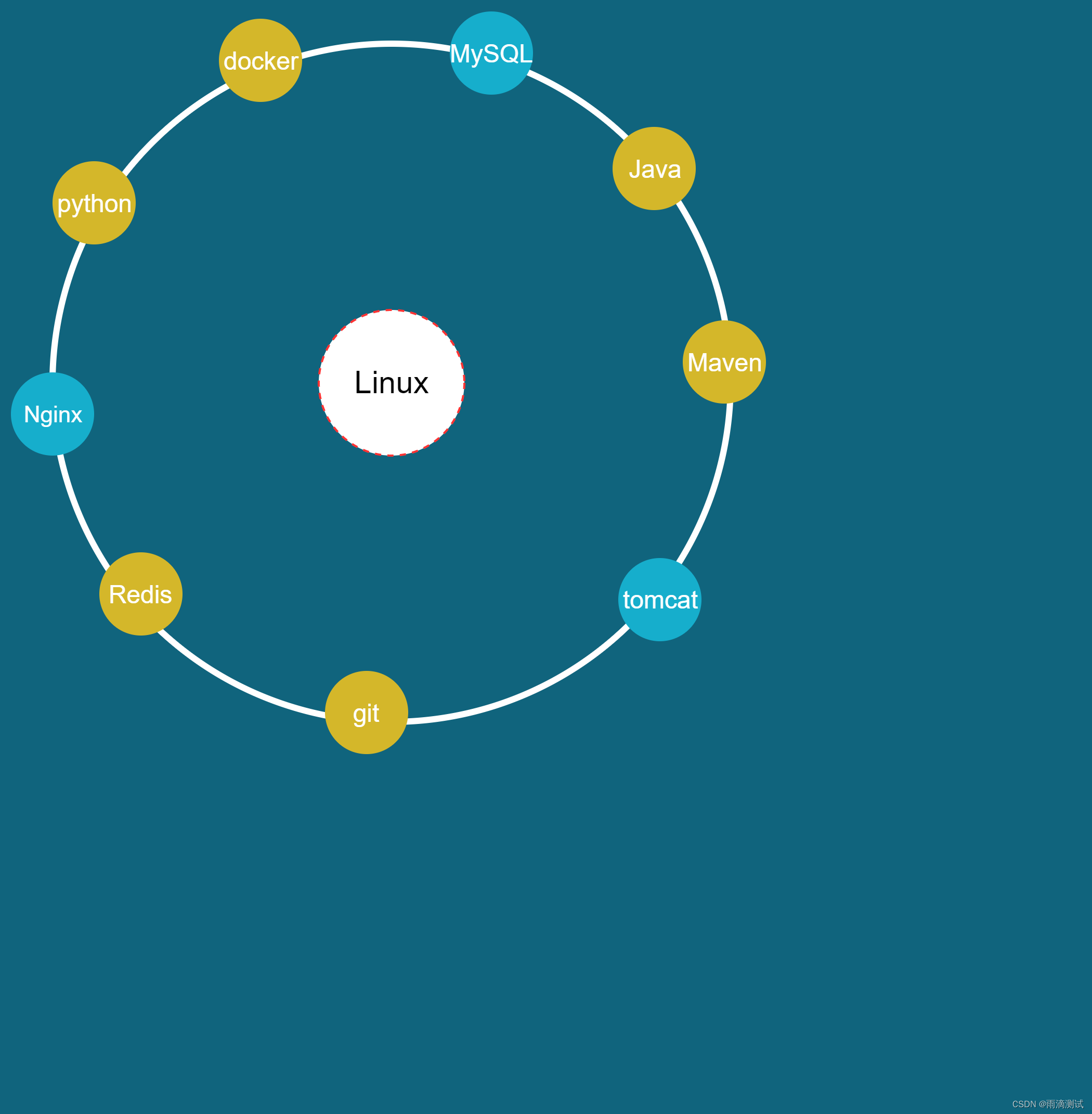
Linux系统下常用软件安装汇总,包括mysql,java,git,redis等
01.环境搭建 1.安装列表 MySQL 5.7.11 Java 1.8 Apache Maven 3.6 tomcat8.5 git Redis Nginx python docker 2.安装mysql 1.拷贝mysql安装文件到Linux的某个目录下 2.解压Linux安装包:tar -xvzf mysql-5.7.32-linux-glibc2.12-x86_64.tar.gz 3.进入解压后…...
)
【Linux】——期末复习题(一)
🎃个人专栏: 🐬 算法设计与分析:算法设计与分析_IT闫的博客-CSDN博客 🐳Java基础:Java基础_IT闫的博客-CSDN博客 🐋c语言:c语言_IT闫的博客-CSDN博客 🐟MySQL:…...

【论文阅读】Speech Driven Video Editing via an Audio-Conditioned Diffusion Model
DiffusionVideoEditing:基于音频条件扩散模型的语音驱动视频编辑 code:GitHub - DanBigioi/DiffusionVideoEditing: Official project repo for paper "Speech Driven Video Editing via an Audio-Conditioned Diffusion Model" paper&#…...
【华为 ICT HCIA eNSP 习题汇总】——题目集4
1、(多选)网络中出现故障后,管理员通过排查发现某台路由器的配置被修改了,那么管理员应该采取哪些措施来避免这种状况再次发生? A、管理员应该通过配置 ACL 来扩展只有管理员能够登录设备 B、管理员应该在路由的管理端…...
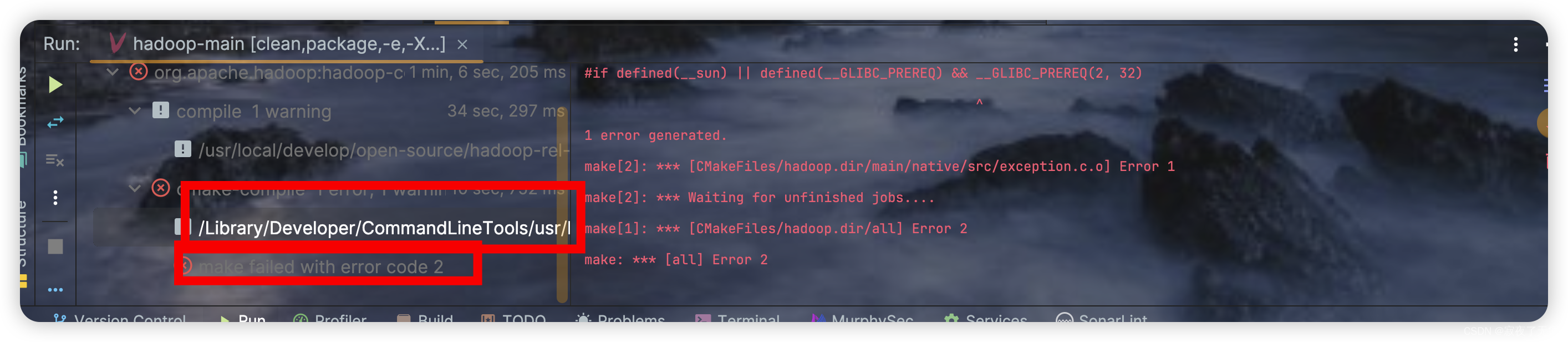
hadoop-common: CMake failed with error code 1
问题 在编译hadoop源码时遇到如下错误 hadoop-common: CMake failed with error code 1 看了这个错误表示一脸懵逼 排查 在mvn 的命令中增加 -X 和 -e mvn clean package -e -X -Pdist,native -DskipTests -Dmaven.javadoc.skip -Dopenssl.prefix/usr/local/bin/openssl 在…...

【面试】-科大讯飞日常实习面试
科大讯飞日常实习面试 提问的问题 面试30min,基本就是介绍项目以及提问java八股文,没有算法题 java保证线程安全的方法 需要根据具体场景选择合适的方法来保证线程安全。java中的异步请求如何实现你的SpringBoot项目怎么匹配在线人数请说出spring springMVC springboot之间的…...

MySQL 数据加密
MySQL 数据加密主要用于保护存储在数据库中的敏感信息,如用户密码、个人身份信息等。MySQL 提供了多种数据加密方法,主要包括: 对称加密: AES_ENCRYPT() 和 AES_DECRYPT() 函数:MySQL 支持使用高级加密标准(…...

8k长序列建模,蛋白质语言模型Prot42仅利用目标蛋白序列即可生成高亲和力结合剂
蛋白质结合剂(如抗体、抑制肽)在疾病诊断、成像分析及靶向药物递送等关键场景中发挥着不可替代的作用。传统上,高特异性蛋白质结合剂的开发高度依赖噬菌体展示、定向进化等实验技术,但这类方法普遍面临资源消耗巨大、研发周期冗长…...

基于服务器使用 apt 安装、配置 Nginx
🧾 一、查看可安装的 Nginx 版本 首先,你可以运行以下命令查看可用版本: apt-cache madison nginx-core输出示例: nginx-core | 1.18.0-6ubuntu14.6 | http://archive.ubuntu.com/ubuntu focal-updates/main amd64 Packages ng…...

全球首个30米分辨率湿地数据集(2000—2022)
数据简介 今天我们分享的数据是全球30米分辨率湿地数据集,包含8种湿地亚类,该数据以0.5X0.5的瓦片存储,我们整理了所有属于中国的瓦片名称与其对应省份,方便大家研究使用。 该数据集作为全球首个30米分辨率、覆盖2000–2022年时间…...

聊一聊接口测试的意义有哪些?
目录 一、隔离性 & 早期测试 二、保障系统集成质量 三、验证业务逻辑的核心层 四、提升测试效率与覆盖度 五、系统稳定性的守护者 六、驱动团队协作与契约管理 七、性能与扩展性的前置评估 八、持续交付的核心支撑 接口测试的意义可以从四个维度展开,首…...

Maven 概述、安装、配置、仓库、私服详解
目录 1、Maven 概述 1.1 Maven 的定义 1.2 Maven 解决的问题 1.3 Maven 的核心特性与优势 2、Maven 安装 2.1 下载 Maven 2.2 安装配置 Maven 2.3 测试安装 2.4 修改 Maven 本地仓库的默认路径 3、Maven 配置 3.1 配置本地仓库 3.2 配置 JDK 3.3 IDEA 配置本地 Ma…...

HashMap中的put方法执行流程(流程图)
1 put操作整体流程 HashMap 的 put 操作是其最核心的功能之一。在 JDK 1.8 及以后版本中,其主要逻辑封装在 putVal 这个内部方法中。整个过程大致如下: 初始判断与哈希计算: 首先,putVal 方法会检查当前的 table(也就…...

springboot整合VUE之在线教育管理系统简介
可以学习到的技能 学会常用技术栈的使用 独立开发项目 学会前端的开发流程 学会后端的开发流程 学会数据库的设计 学会前后端接口调用方式 学会多模块之间的关联 学会数据的处理 适用人群 在校学生,小白用户,想学习知识的 有点基础,想要通过项…...

【笔记】WSL 中 Rust 安装与测试完整记录
#工作记录 WSL 中 Rust 安装与测试完整记录 1. 运行环境 系统:Ubuntu 24.04 LTS (WSL2)架构:x86_64 (GNU/Linux)Rust 版本:rustc 1.87.0 (2025-05-09)Cargo 版本:cargo 1.87.0 (2025-05-06) 2. 安装 Rust 2.1 使用 Rust 官方安…...
详细解析)
Caliper 负载(Workload)详细解析
Caliper 负载(Workload)详细解析 负载(Workload)是 Caliper 性能测试的核心部分,它定义了测试期间要执行的具体合约调用行为和交易模式。下面我将全面深入地讲解负载的各个方面。 一、负载模块基本结构 一个典型的负载模块(如 workload.js)包含以下基本结构: use strict;/…...

怎么让Comfyui导出的图像不包含工作流信息,
为了数据安全,让Comfyui导出的图像不包含工作流信息,导出的图像就不会拖到comfyui中加载出来工作流。 ComfyUI的目录下node.py 直接移除 pnginfo(推荐) 在 save_images 方法中,删除或注释掉所有与 metadata …...
