在 Python 中检查一个数字是否是同构数

更多资料获取
📚 个人网站:ipengtao.com
同构数,又称为自守数或自同构数,是一类特殊的数字,它们具有一种有趣的性质:将其平方后的数字,可以通过某种方式重新排列得到原来的数字。本文将详细介绍在 Python 中如何检查一个数字是否是同构数,并提供丰富的示例代码帮助大家更好地理解这一概念。
什么是同构数?
同构数是一个数字,它的平方数的各位数字可以通过重新排列得到原来的数字。具体来说,如果一个数字 n 的平方数 m,将 m 的各位数字重新排列后可以得到 n,那么 n 就是同构数。例如,25 是同构数,因为 25 的平方是 625,可以将 625 中的数字重新排列为 256,得到原来的数字 25。
同构数的概念在数学和计算机科学中都有应用,它们有一些有趣的性质,例如它们的数量相对较少,而且它们的平方数通常有一些规律。
如何检查一个数字是否是同构数?
要检查一个数字是否是同构数,可以按照以下步骤进行:
- 计算数字的平方。
- 将平方数的各位数字提取出来并进行重新排列。
- 检查重新排列后的数字是否与原始数字相等。
如果重新排列后的数字与原始数字相等,那么这个数字就是同构数。
通过示例代码来演示如何在 Python 中实现这一检查过程。
def is_isomorphic_number(n):# 计算数字的平方square = n * n# 将平方数的各位数字提取出来并排序square_digits = sorted(str(square))# 将原始数字的各位数字提取出来并排序n_digits = sorted(str(n))# 检查重新排列后的数字是否与原始数字相等return square_digits == n_digits# 测试示例
number = 25
if is_isomorphic_number(number):print(f"{number} 是同构数")
else:print(f"{number} 不是同构数")
在上述示例代码中,首先计算数字的平方,并将平方数的各位数字提取出来并排序。然后,将原始数字的各位数字提取出来并排序。最后,检查重新排列后的数字是否与原始数字相等,如果相等,则该数字是同构数。
示例应用场景
同构数虽然在实际编程中的应用有限,但在一些特定情况下仍然具有一定的实际用途。以下是一些示例应用场景以及对应的示例代码:
1. 密码学
同构数的性质可以用于密码学中的数字加密和解密。例如,可以将一个数字视为密文,将其平方数视为解密后的明文。
以下是一个简单的示例:
def encrypt(number):return number ** 2def decrypt(encrypted_number):return int(encrypted_number ** 0.5)original_number = 42
encrypted_number = encrypt(original_number)
decrypted_number = decrypt(encrypted_number)print(f"原始数字:{original_number}")
print(f"加密后的数字:{encrypted_number}")
print(f"解密后的数字:{decrypted_number}")
2. 数学研究
同构数是数学中的一个有趣概念,可以用于数学问题的研究和教学。
例如,可以编写一个程序来查找一定范围内的同构数,并进行数学研究:
def find_isomorphic_numbers_in_range(start, end):isomorphic_numbers = []for number in range(start, end + 1):if is_isomorphic_number(number):isomorphic_numbers.append(number)return isomorphic_numbersstart = 1
end = 10000
isomorphic_numbers = find_isomorphic_numbers_in_range(start, end)
print(f"{start} 到 {end} 范围内的同构数个数:{len(isomorphic_numbers)}")
3. 编程挑战
同构数可以用作编程挑战或面试问题,测试编程能力和数学思维。
例如,编写一个函数来查找前 N 个同构数:
def find_first_n_isomorphic_numbers(n):isomorphic_numbers = []number = 1while len(isomorphic_numbers) < n:if is_isomorphic_number(number):isomorphic_numbers.append(number)number += 1return isomorphic_numbersn = 10
first_n_isomorphic_numbers = find_first_n_isomorphic_numbers(n)
print(f"前 {n} 个同构数:{first_n_isomorphic_numbers}")
4. 数学教育
同构数可以作为数学教育的一个示例,帮助学生理解数字性质和排列组合。
可以编写一个交互式程序,让学生输入一个数字并检查它是否是同构数:
def is_isomorphic_number(number):# 检查是否是同构数的逻辑# ...while True:user_input = input("请输入一个数字(输入 'exit' 退出):")if user_input == 'exit':breaknumber = int(user_input)if is_isomorphic_number(number):print(f"{number} 是同构数!")else:print(f"{number} 不是同构数。")
总结
同构数是一类特殊的数字,它们的平方数的各位数字可以通过重新排列得到原来的数字。在 Python 中,可以通过计算数字的平方、提取各位数字并进行排序,然后检查重新排列后的数字是否与原始数字相等来判断一个数字是否是同构数。虽然同构数在实际编程中用途有限,但它们是数学领域的一个有趣概念,可以用于数学问题的研究和教学。
Python学习路线
更多资料获取
📚 个人网站:ipengtao.com
如果还想要领取更多更丰富的资料,可以点击文章下方名片,回复【优质资料】,即可获取 全方位学习资料包。

点击文章下方链接卡片,回复【优质资料】,可直接领取资料大礼包。
相关文章:

在 Python 中检查一个数字是否是同构数
更多资料获取 📚 个人网站:ipengtao.com 同构数,又称为自守数或自同构数,是一类特殊的数字,它们具有一种有趣的性质:将其平方后的数字,可以通过某种方式重新排列得到原来的数字。本文将详细介绍…...

【 Qt 快速上手】-①- Qt 背景介绍与发展前景
文章目录 1.1 什么是 Qt1.2 Qt 的发展史1.3 Qt 支持的平台1.4 Qt 版本1.5 Qt 的优点1.6 Qt的应用场景1.7 Qt的成功案例1.8 Qt的发展前景及就业分析行业发展方向就业方面的发展前景 1.1 什么是 Qt Qt 是一个跨平台的 C 图形用户界面应用程序框架。它为应用程序开发者提供了建立…...

Kafka-消费者-KafkaConsumer分析-PartitionAssignor
Leader消费者在收到JoinGroupResponse后,会按照其中指定的分区分配策略进行分区分配,每个分区分配策略就是一个PartitionAssignor接口的实现。图是PartitionAssignor的继承结构及其中的组件。 PartitionAssignor接口中定义了Assignment和Subscription两个…...

【办公软件篇】软件启动器Lucy打造自己的工具箱
【办公软件篇】软件启动器Lucy打造自己的工具箱 自从Rolan改为订阅制后就弃用了,本次推荐一款快速启动器Lucy,不联网,不写注册表,体积小,绿色免安装,免费无广告,风格简洁但不简单,目…...

C#MQTT编程08--MQTT服务器和客户端(cmd版)
1、前言 前面完成了winform版,wpf版,为什么要搞个cmd版,因为前面介绍了mqtt的报文结构,重点分析了【连接报文】,【订阅报文】,【发布报文】,这节就要就看看实际报文是怎么组装的,这…...

【高等数学之牛莱公式】
一、深入挖掘定积分 二、变限积分 三、变限积分的"天然"连续性 四、微积分基本定理 五、定积分基本方法 5.1、换元法 5.2、分部积分法 六、定积分经典结论 七、区间再现公式 八、三角函数积分变换公式 九、周期函数积分变换公式 十、分段函数求定积分...

基于HFSS的微带线特性阻抗仿真-与基于FDTD的计算电磁学方法对比(Matlab)
基于HFSS的微带线特性阻抗仿真-与基于FDTD的计算电磁学方法对比(Matlab) 工程下载: HFSS的微带线特性阻抗仿真工程文件(注意版本:HFSS2023R2): https://download.csdn.net/download/weixin_445…...
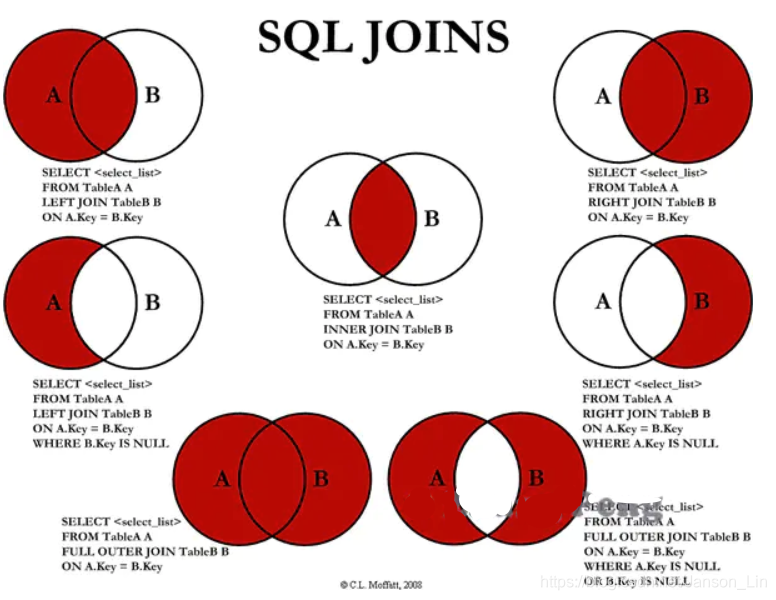
【SQL】SQL语法小结
相关资料 参考链接1:SQL 语法(超级详细) 参考链接2:史上超强最常用SQL语句大全 SQL练习网站:CSDN、牛客、LeetCode、LintCode SQL相关视频: 推荐书籍: 文章目录 数据分析对SQL的要求SQL语法简介…...
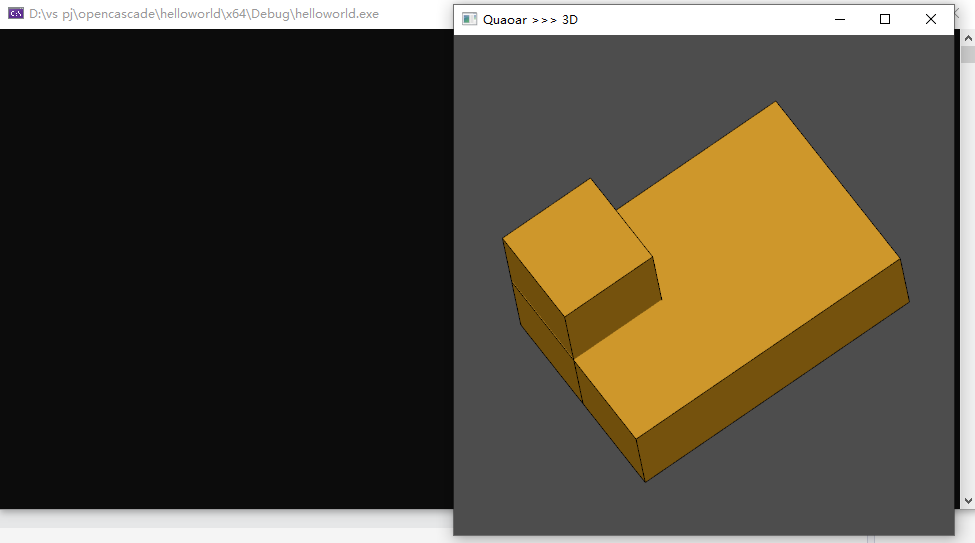
Open CASCADE学习|显示模型
目录 1、编写代码 Viewer.h Viewer.cpp ViewerInteractor.h ViewerInteractor.cpp helloworld.cpp 2、配置 3、编译运行 1、编写代码 Viewer.h #pragma once #ifdef _WIN32 #include <Windows.h> #endif // Local includes #include "ViewerInteract…...
【C++】string的基本使用
从这篇博客开始,我们的C部分就进入到了STL,STL的出现可以说是C发展历史上非常关键的一步,自此C和C语言有了较为明显的差别。那么什么是STL呢? 后来不断的演化,发展成了知名的两个版本,一个叫做P.J.版本&am…...
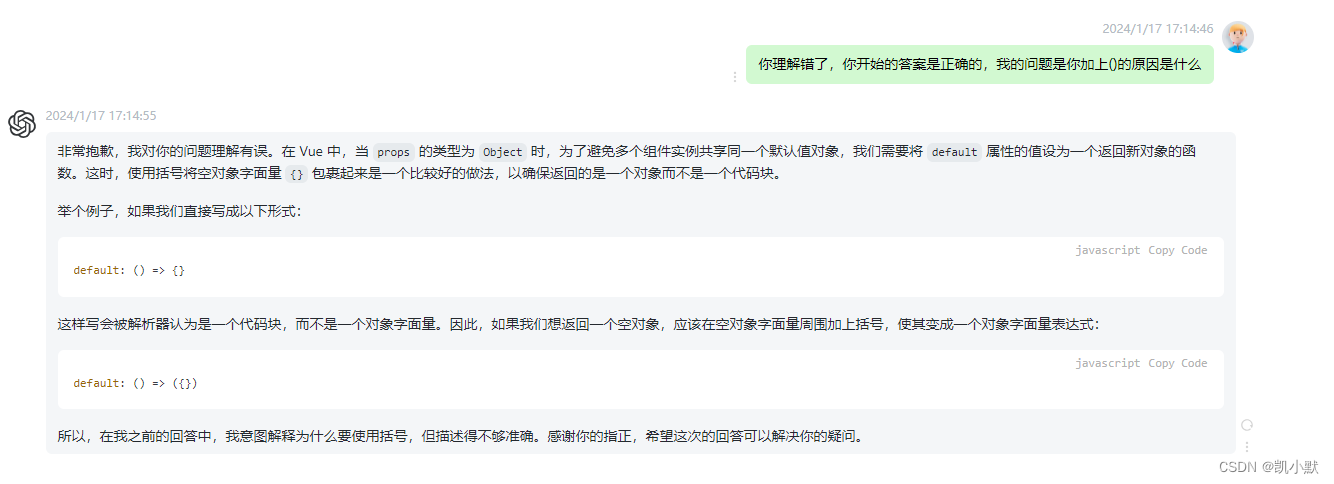
vue 里 props 类型为 Object 时设置 default: () => {} 返回的是 undefined 而不是 {}?
问题 今天遇到个小坑,就是 vue 里使用 props 传参类型为 Object 的时候设置 default: () > {} 报错,具体代码如下 <template><div class"pre-archive-info"><template v-if"infoData.kaimo ! null">{{ infoD…...
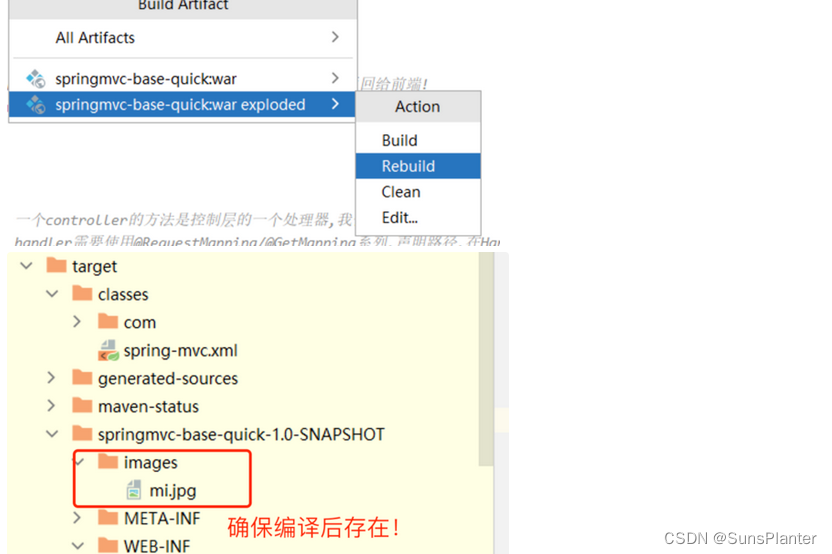
04 SpringMVC响应数据之页面跳转控制+返回JSON数据+返回静态资源
1. handler方法分析 /*** TODO: 一个controller的方法是控制层的一个处理器,我们称为handler* TODO: handler需要使用RequestMapping/GetMapping系列,声明路径,在HandlerMapping中注册,供DS查找!* TODO: handler作用总结:* 1.接收请求参数(param,json,pathVariable,共享…...

Python圣诞主题绘图:用turtle库打造冬日奇妙画面【第31篇—python:圣诞节】
文章目录 Python圣诞主题绘图导言代码结构概览详细解析drawlight函数tree函数xzs函数drawsnow函数五角星的绘制 完整代码代码解析总结 Python圣诞主题绘图 导言 圣诞季节是个充满欢乐和创意的时刻。在这个技术博客中,我们将深入探讨如何使用Python的turtle库创建一…...

[开发语言][c++]:Static关键字和全局变量
Static关键字和全局变量 1. 生命周期、作用域和初始化时机2. 全局变量3. Static 关键字3.1 面向过程3.1.1 静态全局变量3.1.2 静态局部变量(单例中会使用)3.1.3 静态函数 3.2 面向对象3.2.1 类内静态成员变量3.2.2 类内静态成员函数 Reference 写在前面&…...

计算机组成原理 第一弹
ps:本文章的图片来源都是来自于湖科大教书匠高老师的视频,声明:仅供自己复习,里面加上了自己的理解 这里附上视频链接地址:1-2 计算机的发展_哔哩哔哩_bilibili 目录 🚀计算机系统 🚀计…...

Hadoop基础知识
Hadoop基础知识 1、Hadoop简介 广义上来说,Hadoop通常是指一个更广泛的概念——Hadoop生态圈。狭义上说,Hadoop指Apache这款开源框架,它的核心组件有: HDFS(分布式文件系统):解决海量数据存储Y…...

Java进阶之旅第五天
Java进阶之旅第五天 不可变集合 应用场景 1.如果某个数据不能被修改,把它拷贝到不可变集合中是个很好的实践2.当集合对象被不可信的库调用时,不可变形式是安全的3.不可变集合不能修改,只能进行查询 获取方式 在List,Set,Map接口中,都存在静态的of方法,可以获取一个不可变的…...
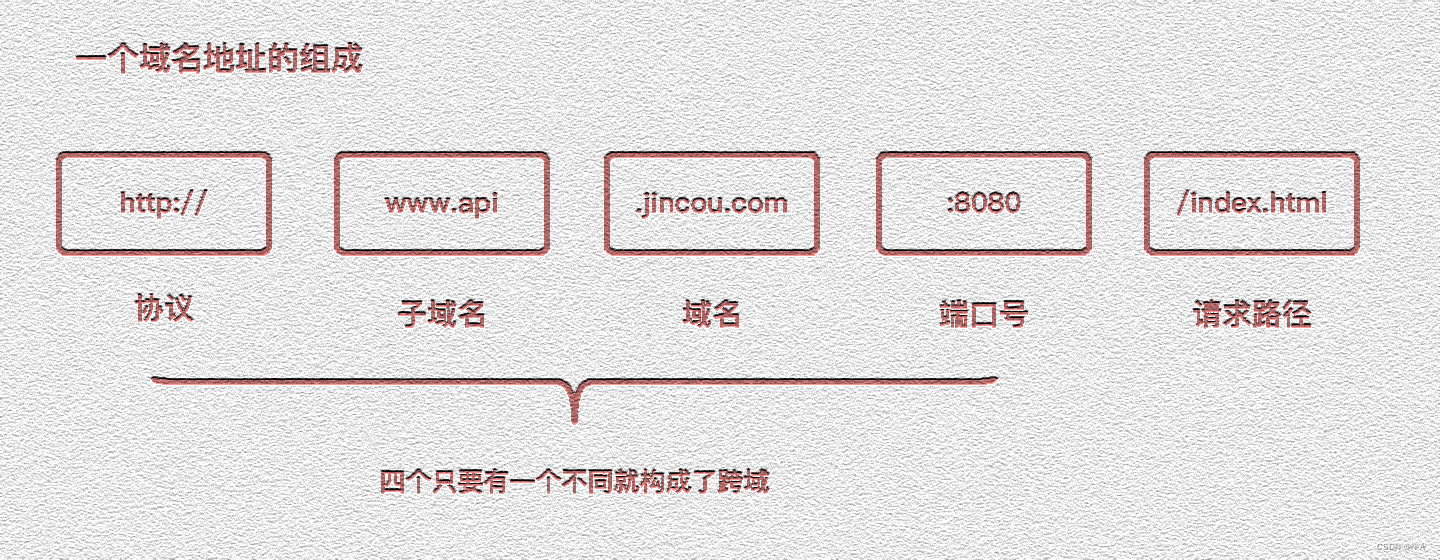
拓展边界:前端世界的跨域挑战
目录 什么是跨域 概念 同源策略及限制内容 常见跨域场景 如何解决跨域 CORS Nginx代理跨域 Node中间件代理跨域 WebSocket postMessage JSONP 其他 什么是跨域 概念 在此之前,我们了解一下一个域名地址的组成: 跨域指的是在网络安全中&…...
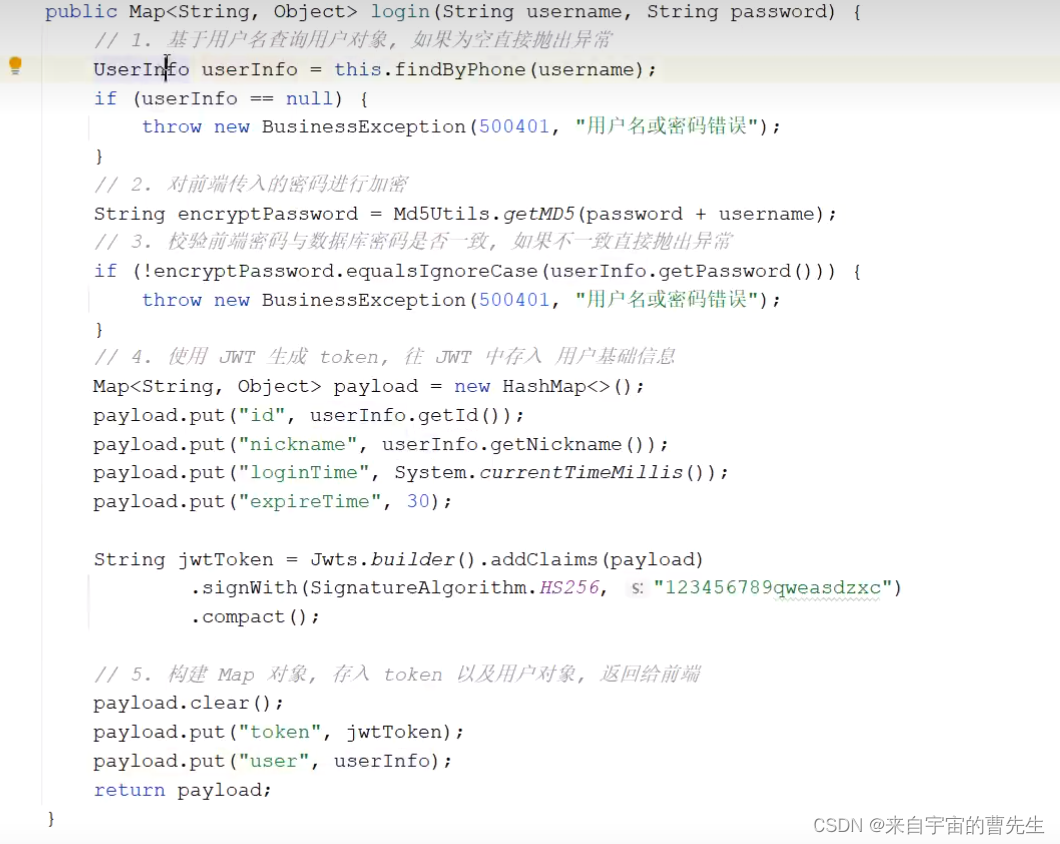
旅游项目day03
1. 前端整合后端发短信接口 2. 注册功能 后端提供注册接口,接受前端传入的参数,创建新的用户对象,保存到数据库。 接口设计: 实现步骤: 手机号码唯一性校验(后端一定要再次校验手机号唯一性)…...
)
单片机学习记录(一)
简答题 第1章 1.微处理器、微计算机、CPU、单片机、嵌入式处理器他们之间有何区别? 答:微处理器、CPU都是中央处理器的不同称谓,微处理器芯片本身不是计算机; 单片机、微计算机都是一个完整的计算机系统,单片机是集…...

深度学习在微纳光子学中的应用
深度学习在微纳光子学中的主要应用方向 深度学习与微纳光子学的结合主要集中在以下几个方向: 逆向设计 通过神经网络快速预测微纳结构的光学响应,替代传统耗时的数值模拟方法。例如设计超表面、光子晶体等结构。 特征提取与优化 从复杂的光学数据中自…...

C++初阶-list的底层
目录 1.std::list实现的所有代码 2.list的简单介绍 2.1实现list的类 2.2_list_iterator的实现 2.2.1_list_iterator实现的原因和好处 2.2.2_list_iterator实现 2.3_list_node的实现 2.3.1. 避免递归的模板依赖 2.3.2. 内存布局一致性 2.3.3. 类型安全的替代方案 2.3.…...

Qt/C++开发监控GB28181系统/取流协议/同时支持udp/tcp被动/tcp主动
一、前言说明 在2011版本的gb28181协议中,拉取视频流只要求udp方式,从2016开始要求新增支持tcp被动和tcp主动两种方式,udp理论上会丢包的,所以实际使用过程可能会出现画面花屏的情况,而tcp肯定不丢包,起码…...

k8s从入门到放弃之Ingress七层负载
k8s从入门到放弃之Ingress七层负载 在Kubernetes(简称K8s)中,Ingress是一个API对象,它允许你定义如何从集群外部访问集群内部的服务。Ingress可以提供负载均衡、SSL终结和基于名称的虚拟主机等功能。通过Ingress,你可…...

【Java学习笔记】Arrays类
Arrays 类 1. 导入包:import java.util.Arrays 2. 常用方法一览表 方法描述Arrays.toString()返回数组的字符串形式Arrays.sort()排序(自然排序和定制排序)Arrays.binarySearch()通过二分搜索法进行查找(前提:数组是…...

前端导出带有合并单元格的列表
// 导出async function exportExcel(fileName "共识调整.xlsx") {// 所有数据const exportData await getAllMainData();// 表头内容let fitstTitleList [];const secondTitleList [];allColumns.value.forEach(column > {if (!column.children) {fitstTitleL…...

江苏艾立泰跨国资源接力:废料变黄金的绿色供应链革命
在华东塑料包装行业面临限塑令深度调整的背景下,江苏艾立泰以一场跨国资源接力的创新实践,重新定义了绿色供应链的边界。 跨国回收网络:废料变黄金的全球棋局 艾立泰在欧洲、东南亚建立再生塑料回收点,将海外废弃包装箱通过标准…...

高等数学(下)题型笔记(八)空间解析几何与向量代数
目录 0 前言 1 向量的点乘 1.1 基本公式 1.2 例题 2 向量的叉乘 2.1 基础知识 2.2 例题 3 空间平面方程 3.1 基础知识 3.2 例题 4 空间直线方程 4.1 基础知识 4.2 例题 5 旋转曲面及其方程 5.1 基础知识 5.2 例题 6 空间曲面的法线与切平面 6.1 基础知识 6.2…...

数据链路层的主要功能是什么
数据链路层(OSI模型第2层)的核心功能是在相邻网络节点(如交换机、主机)间提供可靠的数据帧传输服务,主要职责包括: 🔑 核心功能详解: 帧封装与解封装 封装: 将网络层下发…...

Python爬虫(一):爬虫伪装
一、网站防爬机制概述 在当今互联网环境中,具有一定规模或盈利性质的网站几乎都实施了各种防爬措施。这些措施主要分为两大类: 身份验证机制:直接将未经授权的爬虫阻挡在外反爬技术体系:通过各种技术手段增加爬虫获取数据的难度…...
