C语言每日一题】——杨氏矩阵
【C语言每日一题】——倒置字符串😎
- 前言🙌
- 杨氏矩阵🙌
- 总结撒花💞

😎博客昵称:博客小梦
😊最喜欢的座右铭:全神贯注的上吧!!!
😊作者简介:一名热爱C/C++,算法等技术、喜爱运动、热爱K歌、敢于追梦的小博主!
😘博主小留言:哈喽!😄各位CSDN的uu们,我是你的博客好友小梦,希望我的文章可以给您带来一定的帮助,话不多说,文章推上!欢迎大家在评论区唠嗑指正,觉得好的话别忘了一键三连哦!😘
前言🙌
哈喽各位友友们😊,我今天又学到了很多有趣的知识,现在迫不及待的想和大家分享一下!😘我仅已此文,和大家分享C语言每日一题】——杨氏矩阵~这里利用了数组指针的方法知识, 都是精华内容,可不要错过哟!!!😍😍😍
杨氏矩阵🙌
题目简述:
有一个数字矩阵,矩阵的每行从左到右是递增的,矩阵从上到下是递增的,请编写程序在这样的矩阵中查找某个数字是否存在。
要求: 时间复杂度小于O(N);
解题思路分析: 😍
- 这里要求 时间复杂度小于O(N);所以利用常规的遍历一遍数组的方法是不满足的。因为遍历数组的时间复杂度是O(N)。
- 首先认真读题,分析解题思路。因为矩阵的每行从左到右是递增的,矩阵从上到下是递增的,所以第一行的最后一个元素就是这一行的最大值,也是这个元素所在列的最小值。每一行的最后一个元素都是该行的最大值。
- 第一步就是拿第一行的最后一个元素与我们查找的元素进行大小比较。
- 如果比我们的 k 要大,在我说明该元素一定在该行上,或者不存在 。让 j - - ,对该行逐个逐个进行两两比较 。
- 如果比我们的 k 要小,在我说明该元素一定在下一行上,或者不存在 。让 i + + ,对该列逐个逐个进行两两比较 。
- 然后循环重复上述操作,直到找到元素后,再跳出循环。-这里定义一个flag 变量目的是为了将没有找到元素的信息打印出来,这也是题目的要求之一**
- 按照这种方法时间复杂度是小于O(N)。
画图分析: 😍

解题源码分享: 😍
#include<stdio.h>void Find(int(*a)[3], int row, int col,int k)
{int i = 0;int flag = 0;int j = col - 1;while ((i>= 0 && i <= row - 1) && (j >= 0 && j <= col - 1) ){if (*(*(a + i) + j) > k){j--;}else if(*(*(a + i) + j) < k){i++;}else{flag = 1;printf("找到了元素,其下标为:%d ,%d\n", i, j);break;}}if(flag == 0)printf("找不到该元素\n");
}int main()
{int a[3][3] = { {1,2,3},{4,5,6}, {7,8,9} };int row = sizeof(a[0]) / sizeof(int);int col = sizeof(a) / sizeof(a[0]);int k = 0;scanf("%d", &k);Find(a,row,col,k);return 0;
}
程序输出结果验证: 😊
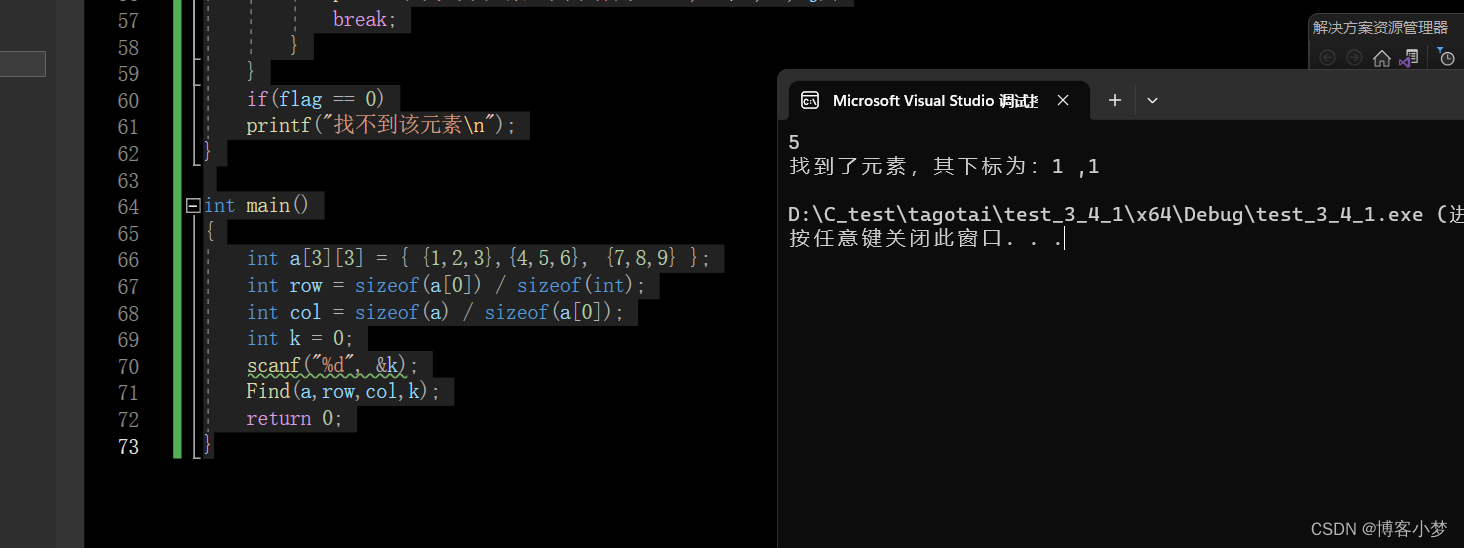
总结撒花💞
本篇文章旨在分享C语言详解C语言每日一题】——杨氏矩阵。希望大家通过阅读此文有所收获!😘如果我写的有什么不好之处,请在文章下方给出你宝贵的意见😊。如果觉得我写的好的话请点个赞赞和关注哦~😘😘😘
相关文章:

C语言每日一题】——杨氏矩阵
【C语言每日一题】——倒置字符串😎前言🙌杨氏矩阵🙌总结撒花💞😎博客昵称:博客小梦 😊最喜欢的座右铭:全神贯注的上吧!!! 😊作者简介…...
最佳iOS设备管理器imazing 2.16.9官网Mac/Windows下载电脑版怎么下载安装
imazing 2.16.9官网Mac/Windows下载电脑版是款针对苹果设备所打造的管理工具。iMazing为用户提供多种设备管理功能,每一位用户都能以自己的形式管理苹果设备。iMazing与苹果设备连接后,用户就可以轻松传输文件,浏览保存信息等。 应用介绍 iM…...

八大排序算法之堆排序的实现+经典TopK问题
目录 一.堆元素的上下调整接口 1.前言 2.堆元素向上调整算法接口 3.堆元素向下调整算法接口 二.堆排序的实现 1.空间复杂度为O(N)的堆排序(以排升序为例) 思路分析: 代码实现: 排序测试: 时空复杂度分析: 2. 空间复杂度为O(1)的堆排序(以排降序为例) 将数组arr调…...
使用AppSmith(PagePlug )低代码平台快速构建小程序应用实践
文章目录一、入门(一)介绍(二)功能特性(三)体验一下(四)参考教程二、使用Appsmith构建商城微信小程序(一)说明(二)应用配置࿰…...

第52章 短信验证服务和登录的后端定义实现
1 Services.Messages.SmsValidate using Core.Domain.Messages; using Data; using Microsoft.EntityFrameworkCore; namespace Services.Messages { /// <summary> /// 【短信验证服务--类】 /// <remarks> /// 摘要: /// 通过类中的方法成员实…...
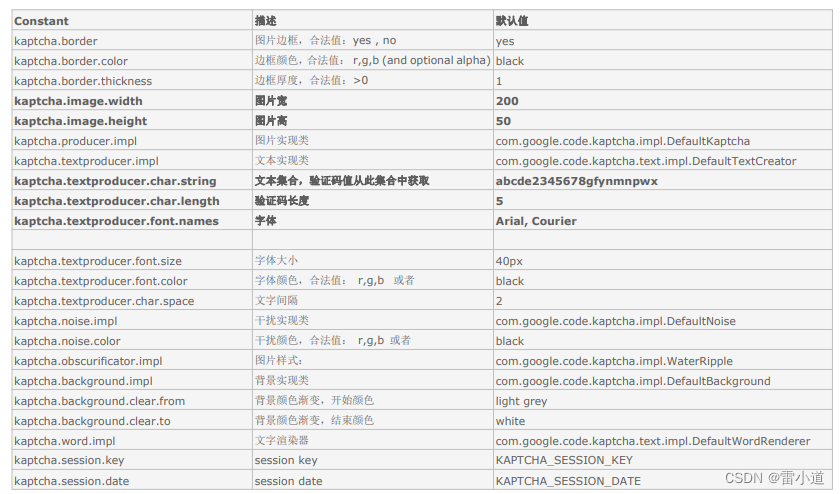
谷歌验证码的使用
1. 表单重复提交之验证码 1.1 表单重复提交三种常见情况 提交完表单。服务器使用请求转来进行页面跳转。这个时候,用户按下功能键 F5,就会发起最后一次的请求。造成表单重复提交问题。解决方法:使用重定向来进行跳转用户正常提交服务器&…...
- git的安装与配置)
Git学习入门(1)- git的安装与配置
title: git学习(1) - git的安装与配置CSDN: https://blog.csdn.net/jj6666djdbbd?typeblogBlog: https://helloylh.comGithub: https://github.com/luumodtags: gitabbrlink: 12001description: 本文主要讲解了git的安装,配置基本工作date: …...

【Python】使用Playwright断言方法验证网页和Web应用程序状态
作为测试框架,Playwright 提供了一系列断言方法,您可以使用它们来验证网页和 Web 应用程序的状态。在这篇博客中,田辛老师将介绍 Playwright 中可用的各种断言方法,并为每种方法提供示例。 assert page.url() expected_url &…...

libgdx导入blender模型
具体就是参考 官网 https://libgdx.com/wiki/graphics/3d/importing-blender-models-in-libgdx blender 教程可以看八个案例教程带你从0到1入门blender【已完结】 这里贴一下过程图。 1.初始环境搭建略过。 2.打开blender 选中摄像机和灯光,右键进行删除。 3.选中…...
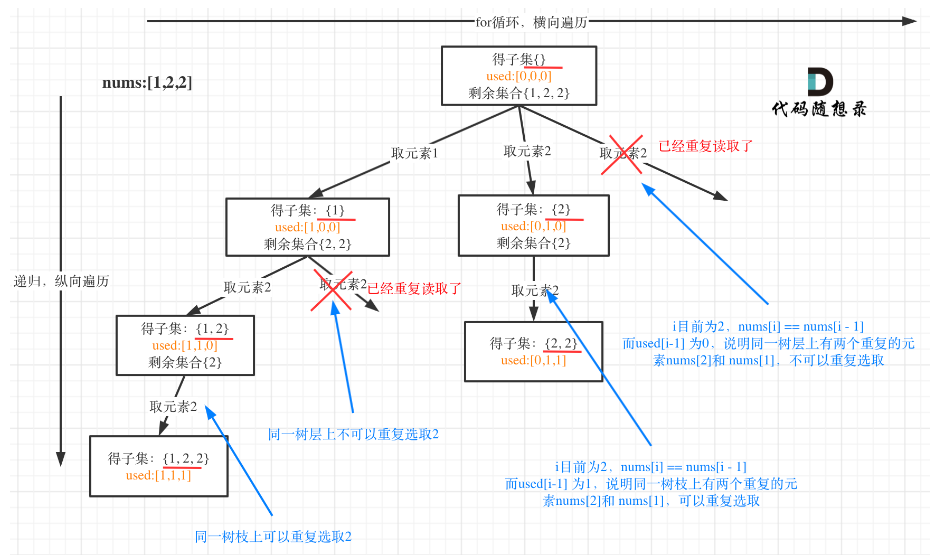
【20230227】回溯算法小结
回溯法又叫回溯搜索法,是搜索的一种方式。回溯法本质是穷举所有可能。如果想让回溯法高效一些,可以加一些剪枝操作。回溯算法解决的经典问题:组合问题切割问题子集问题排列问题棋盘问题如何去理解回溯法?回溯法解决的问题都可以抽…...
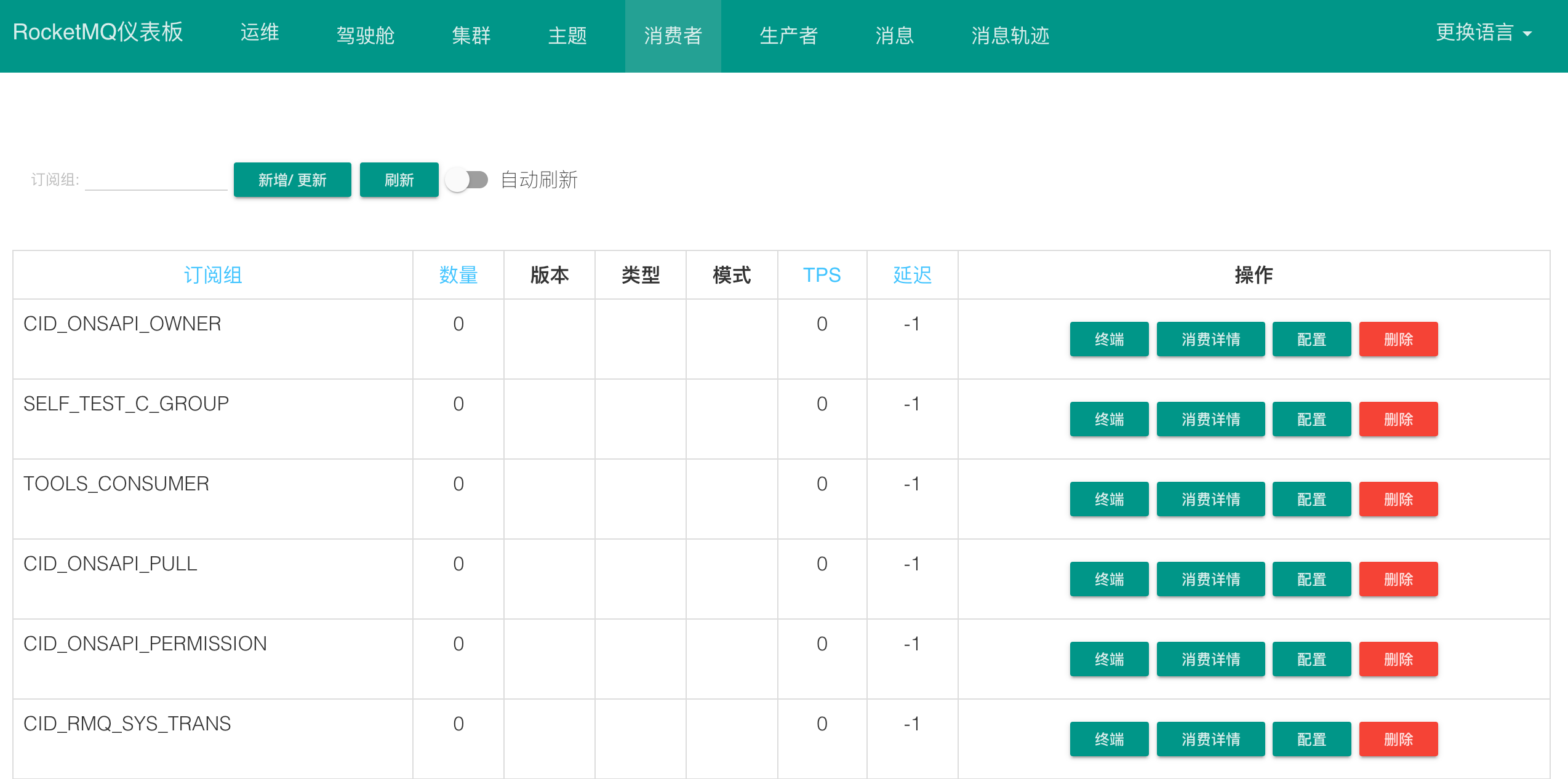
centos安装rocketmq
centos安装rocketmq1 下载rocketmq二进制包2 解压二进制包3 修改broker.conf4 修改runbroker.sh和runserver.sh的JVM参数5 启动NameServer和Broker6 安装rockermq dashboard(可视化控制台)1 下载rocketmq二进制包 点击rocketmq二进制包下载地址,下载完成之后通过ft…...
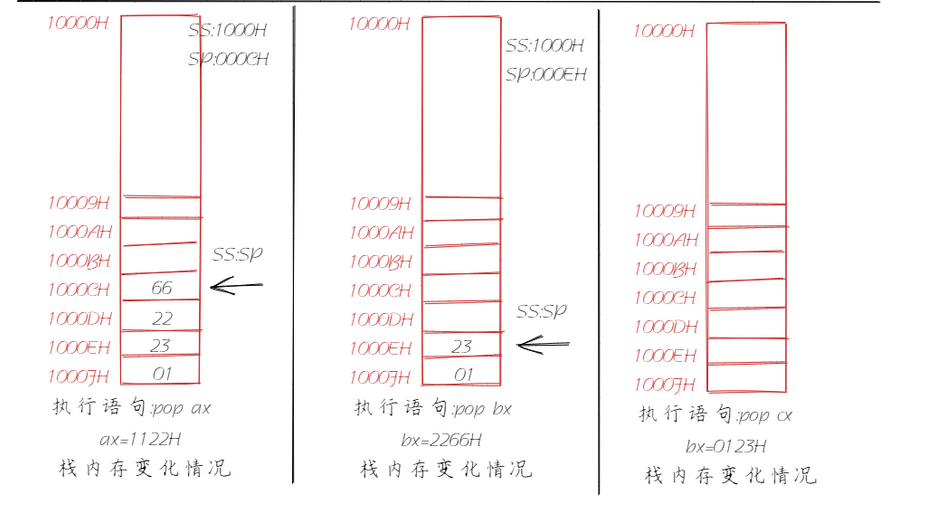
汇编语言程序设计(二)之寄存器
系列文章 汇编语言程序设计(一) 寄存器 在学习汇编的过程中,我们经常需要操作寄存器,那么寄存器又是什么呢?它是用来干什么的? 它有什么分类?又该如何操作?… 你可能会有许多的…...

华为OD机试Golang解题 - 单词接龙 | 独家
华为Od必看系列 华为OD机试 全流程解析+经验分享,题型分享,防作弊指南)华为od机试,独家整理 已参加机试人员的实战技巧华为od 2023 | 什么是华为od,od 薪资待遇,od机试题清单华为OD机试真题大全,用 Python 解华为机试题 | 机试宝典文章目录 华为Od必看系列使用说明本期题目…...

Elasticsearch的搜索命令
Elasticsearch的搜索命令 文章目录Elasticsearch的搜索命令数据准备URI Searchq(查询字符串)analyzer(指定查询字符串时使用的分析器)df(指定查询字段)_source(指定返回文档的字段)s…...

为什么人们宁可用Lombok,也不把成员设为public?
目录专栏导读一、从零了解JavaBean1、基本概念2、JavaBean的特征3、JavaBean的优点二、定义最简单的JavaBean三、思考一个问题,为何属性是private,然后用get/set方法?四、下面系统的分析以下,why?五、不和谐的声音,禁…...
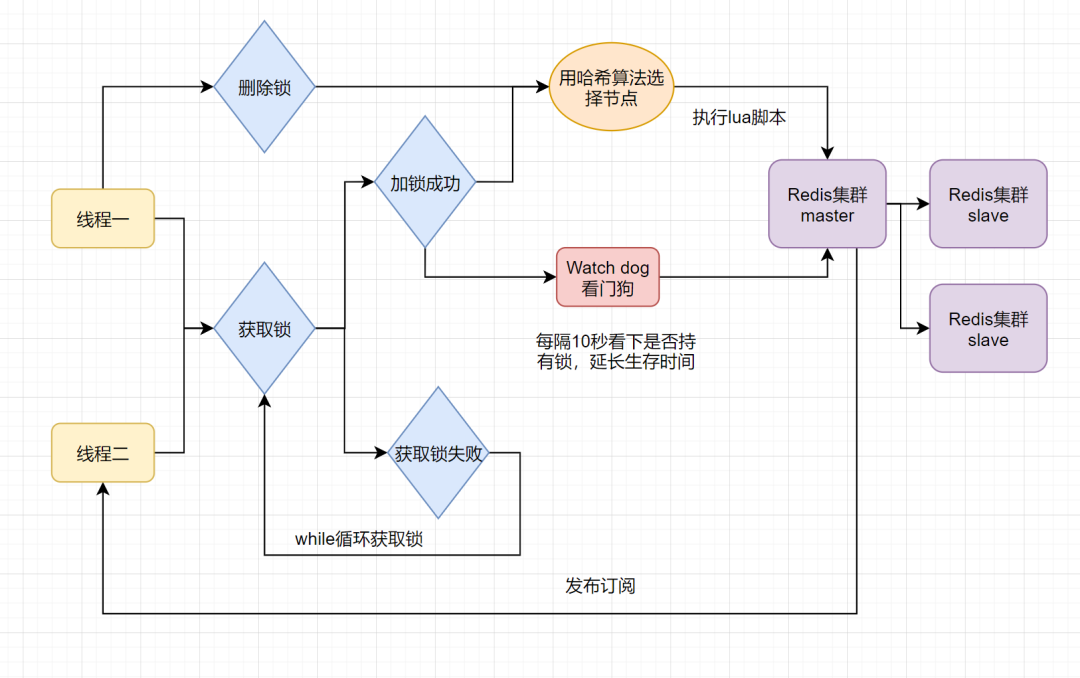
【Redis】Redis 如何实现分布式锁
Redis 如何实现分布式锁1. 什么是分布式锁1.1 分布式锁的特点1.2 分布式锁的场景1.3 分布式锁的实现方式2. Redis 实现分布式锁2.1 setnx expire2.2 set ex px nx2.3 set ex px nx 校验唯一随机值,再删除2.4 Redisson 实现分布式锁1. 什么是分布式锁 分布式锁其实…...
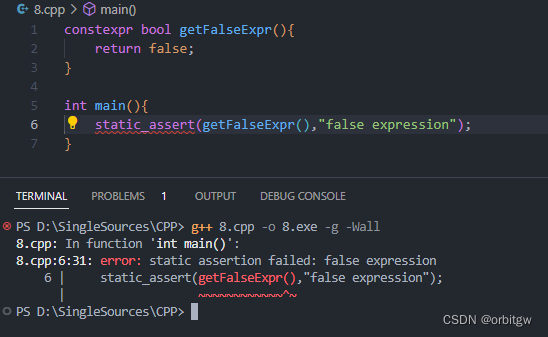
C++ 断言
文章目录前言assertstatic_assert前言 断言(Assertion)是一种常用的编程手段,用于排除程序中不应该出现的逻辑错误。它是一种很好的Debug工具。其作用是判断表达式是否为真。C提供了assert和static_assert来进行断言。在C库中也有断言,其中断言与C的相同…...
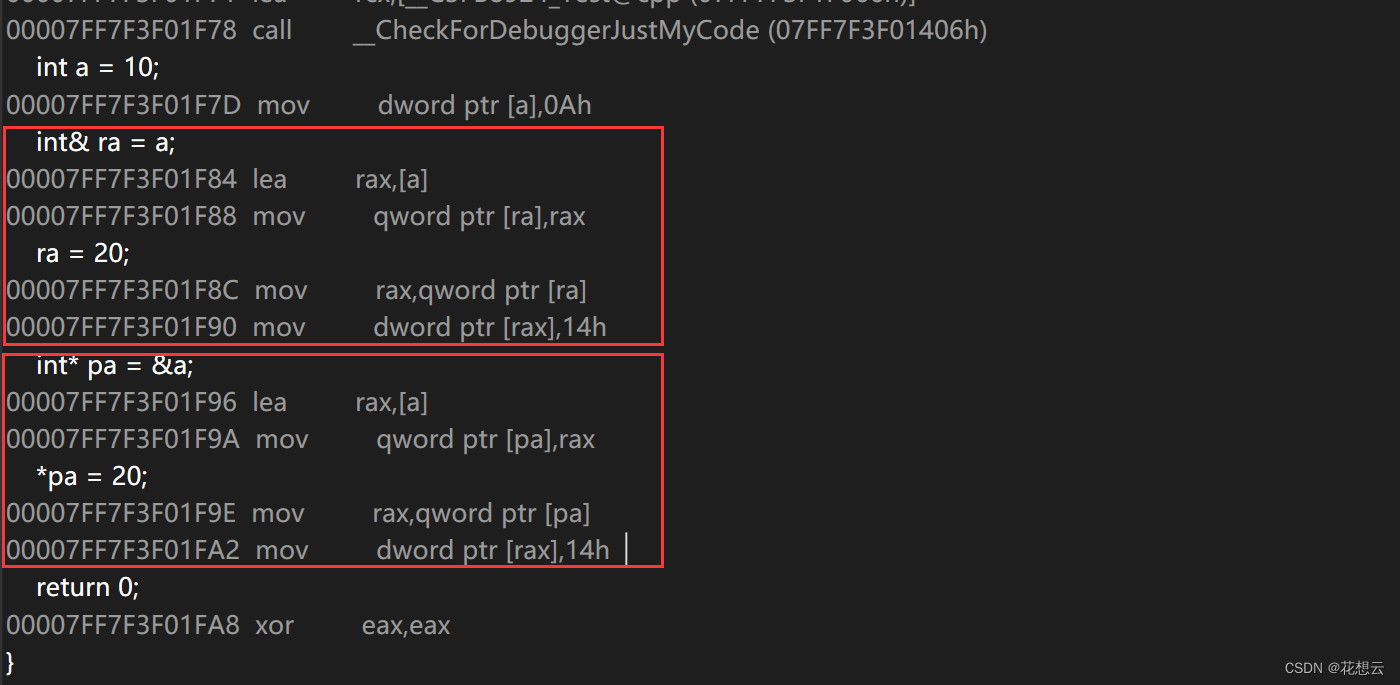
C++修炼之练气期第五层——引用
目录 1.引用的概念 2.引用的性质 3.常量引用 4.使用场景 1.作参数 2.作返回值 5.传值与传引用的效率比较 6.值和引用作为返回值的性能比较 7.引用与指针 指针与引用的不同点 要说C语言中哪个知识点最难学难懂,大部分人可能和我一样的答案——指针。C既然…...
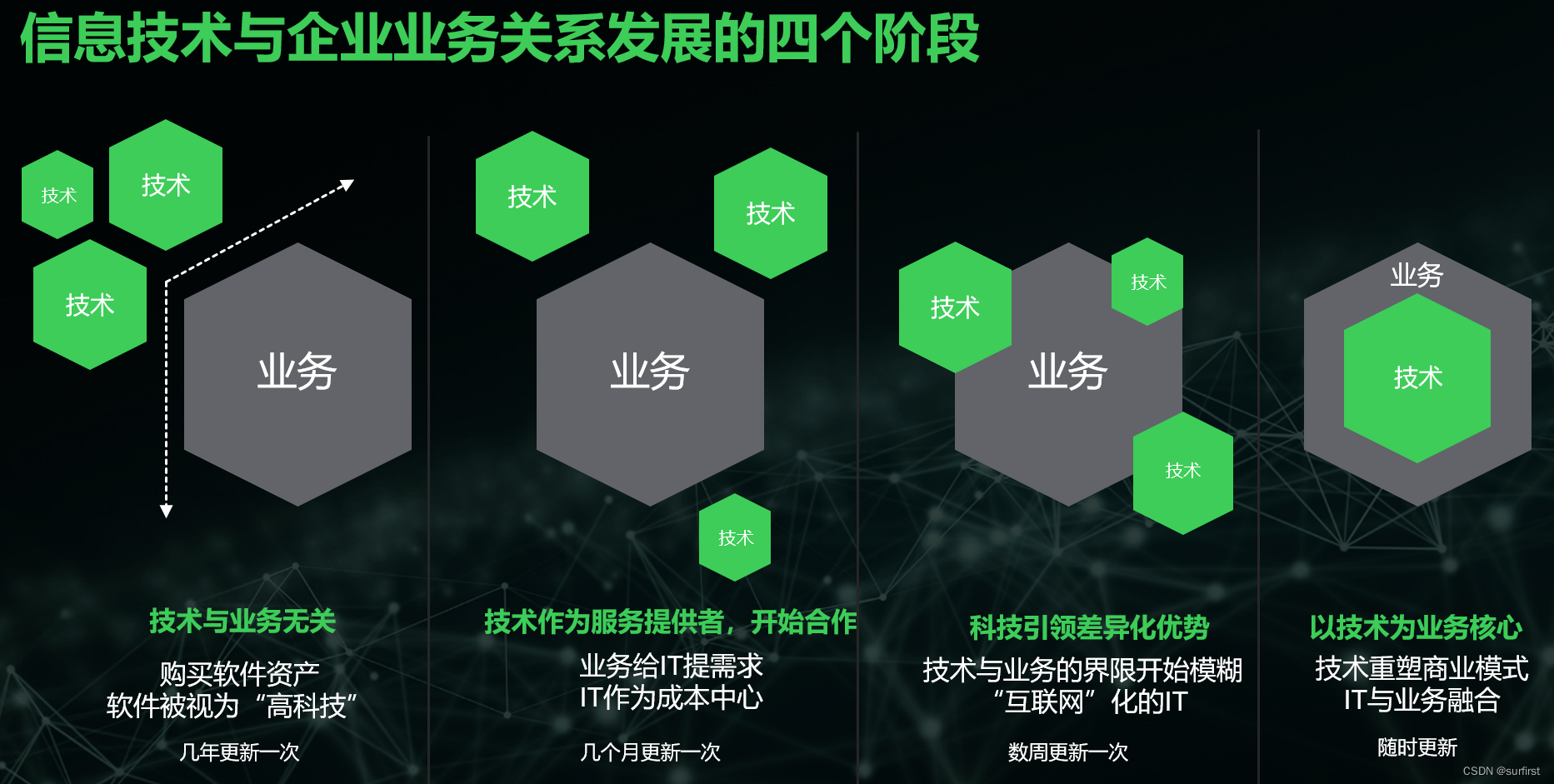
从企业数字化发展的四个阶段,看数字化创新战略
《Edge: Value-Driven Digital Transformation》一书根据信息技术与企业业务发展的关系把企业的数字化分为了四个阶段: 技术与业务无关技术作为服务提供者开始合作科技引领差异化优势以技术为业务核心 下图展示了这四个阶段的特点: 通过了解和分析各个…...
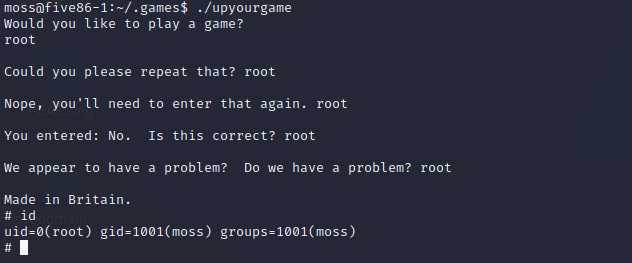
vulnhub five86-1
总结:私钥登录,隐藏文件很多 目录 下载地址 漏洞分析 信息收集 网站渗透 爆破密码 提权 下载地址 Five86-1.zip (Size: 865 MB)Download (Mirror): https://download.vulnhub.com/five86/Five86-1.zip使用:下载以后打开压缩包,使用vm直…...

[特殊字符] 智能合约中的数据是如何在区块链中保持一致的?
🧠 智能合约中的数据是如何在区块链中保持一致的? 为什么所有区块链节点都能得出相同结果?合约调用这么复杂,状态真能保持一致吗?本篇带你从底层视角理解“状态一致性”的真相。 一、智能合约的数据存储在哪里…...

SCAU期末笔记 - 数据分析与数据挖掘题库解析
这门怎么题库答案不全啊日 来简单学一下子来 一、选择题(可多选) 将原始数据进行集成、变换、维度规约、数值规约是在以下哪个步骤的任务?(C) A. 频繁模式挖掘 B.分类和预测 C.数据预处理 D.数据流挖掘 A. 频繁模式挖掘:专注于发现数据中…...

CentOS下的分布式内存计算Spark环境部署
一、Spark 核心架构与应用场景 1.1 分布式计算引擎的核心优势 Spark 是基于内存的分布式计算框架,相比 MapReduce 具有以下核心优势: 内存计算:数据可常驻内存,迭代计算性能提升 10-100 倍(文档段落:3-79…...

《用户共鸣指数(E)驱动品牌大模型种草:如何抢占大模型搜索结果情感高地》
在注意力分散、内容高度同质化的时代,情感连接已成为品牌破圈的关键通道。我们在服务大量品牌客户的过程中发现,消费者对内容的“有感”程度,正日益成为影响品牌传播效率与转化率的核心变量。在生成式AI驱动的内容生成与推荐环境中࿰…...

成都鼎讯硬核科技!雷达目标与干扰模拟器,以卓越性能制胜电磁频谱战
在现代战争中,电磁频谱已成为继陆、海、空、天之后的 “第五维战场”,雷达作为电磁频谱领域的关键装备,其干扰与抗干扰能力的较量,直接影响着战争的胜负走向。由成都鼎讯科技匠心打造的雷达目标与干扰模拟器,凭借数字射…...

代理篇12|深入理解 Vite中的Proxy接口代理配置
在前端开发中,常常会遇到 跨域请求接口 的情况。为了解决这个问题,Vite 和 Webpack 都提供了 proxy 代理功能,用于将本地开发请求转发到后端服务器。 什么是代理(proxy)? 代理是在开发过程中,前端项目通过开发服务器,将指定的请求“转发”到真实的后端服务器,从而绕…...

docker 部署发现spring.profiles.active 问题
报错: org.springframework.boot.context.config.InvalidConfigDataPropertyException: Property spring.profiles.active imported from location class path resource [application-test.yml] is invalid in a profile specific resource [origin: class path re…...

20个超级好用的 CSS 动画库
分享 20 个最佳 CSS 动画库。 它们中的大多数将生成纯 CSS 代码,而不需要任何外部库。 1.Animate.css 一个开箱即用型的跨浏览器动画库,可供你在项目中使用。 2.Magic Animations CSS3 一组简单的动画,可以包含在你的网页或应用项目中。 3.An…...

淘宝扭蛋机小程序系统开发:打造互动性强的购物平台
淘宝扭蛋机小程序系统的开发,旨在打造一个互动性强的购物平台,让用户在购物的同时,能够享受到更多的乐趣和惊喜。 淘宝扭蛋机小程序系统拥有丰富的互动功能。用户可以通过虚拟摇杆操作扭蛋机,实现旋转、抽拉等动作,增…...

android RelativeLayout布局
<?xml version"1.0" encoding"utf-8"?> <RelativeLayout xmlns:android"http://schemas.android.com/apk/res/android"android:layout_width"match_parent"android:layout_height"match_parent"android:gravity&…...

